基于FOA算法的光伏发电MPPT仿真研究

杜 炜，韩 伟，陈 凌，谈友飞

(1.南京南瑞太阳能科技有限公司，江苏南京211106；2.河海大学能源与电气学院，江苏南京211100)

基于FOA算法的光伏发电MPPT仿真研究

杜 炜1，韩 伟2，陈 凌2，谈友飞1

(1.南京南瑞太阳能科技有限公司，江苏南京211106；2.河海大学能源与电气学院，江苏南京211100)

在光伏发电系统中需要对光伏阵列的最大功率点进行跟踪控制以提高整体系统的输出功率。以光伏阵列输出非线性特性为切入点展开研究，在分析了常规算法的优缺点基础上，针对其最大功率点跟踪(MPPT)动态和稳态性能不佳等问题，提出了将果蝇优化算法(FOA)应用于光伏发电系统中。在Matlab/Simulink下进行了建模和仿真，仿真结果表明该方法能够迅速准确地跟踪光伏阵列的最大功率点，防止算法跟踪方向误判情况的发生，表现出良好的动态和稳态特性，同时也证实了算法的正确性和有效性。

果蝇优化算法；光伏发电；最大功率点跟踪；适应度函数

在任何时刻，光伏阵列输出特性具有明显的非线性，且都存在唯一的最大功率输出工作点，并随着太阳辐照强度和温度的变化而变化。因此，只有实时调整光伏阵列的工作点，才能提高光伏发电系统的整体输出效率，使其运行稳定在最大功率点处，这一过程称为最大功率点跟踪 (Maximum Power Point Tracking，简称MPPT)[1]。

本质上，MPPT是一个动态寻优的过程，即通过控制光伏阵列两端电压来控制最大功率的输出。目前较常采用的MPPT控制方法主要包括恒定电压法、扰动观察法、电导增量法、功率回授法、最优梯度法、模糊控制法等[2-5]。其中，恒定电压法受结温影响较大，控制精度相对较低；扰动观察法在MPP附近振荡运行，导致功率损耗一直存在，在特定的情况下会判断错误；电导增量法对系统硬件的要求较高；最优梯度法当太阳辐照强度变化迅速时，MPP将会出现误判现象；传统模糊控制的隶属度函数所特有的性质使其在MPP附近来回摆动，仍然无法消除振荡现象。

基于此，本文先对果蝇优化算法 (Fly Optimization Algorithm，简称FOA)进行了理论分析，并将其应用于光伏阵列MPPT中，且在Matlab/Simulink环境下建立系统仿真模型。仿真结果表明，该算法能够高效、准确地找到系统的最大功率点，同时系统输出功率在MPP附近存在的振荡现象得以有效地消除，从而提高了整个系统的输出功率。

1 光伏阵列的模型和特性

光伏阵列终端特性由实验结果测得，在实际中使用的等效电路如图1所示。

由图1可得光伏阵列的输出电流、电压关系如下式所示[6]：

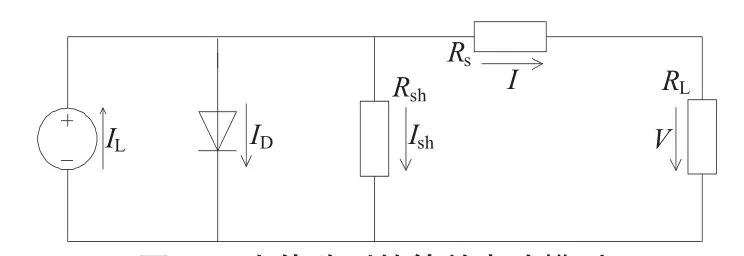
图1 光伏阵列的等效电路模型

在式(1)的基础上进行近似分析，可忽略项，因为通常情况下该项远小于光电流；设定=，因为在正常情况下远小于二极管正向导通电阻。

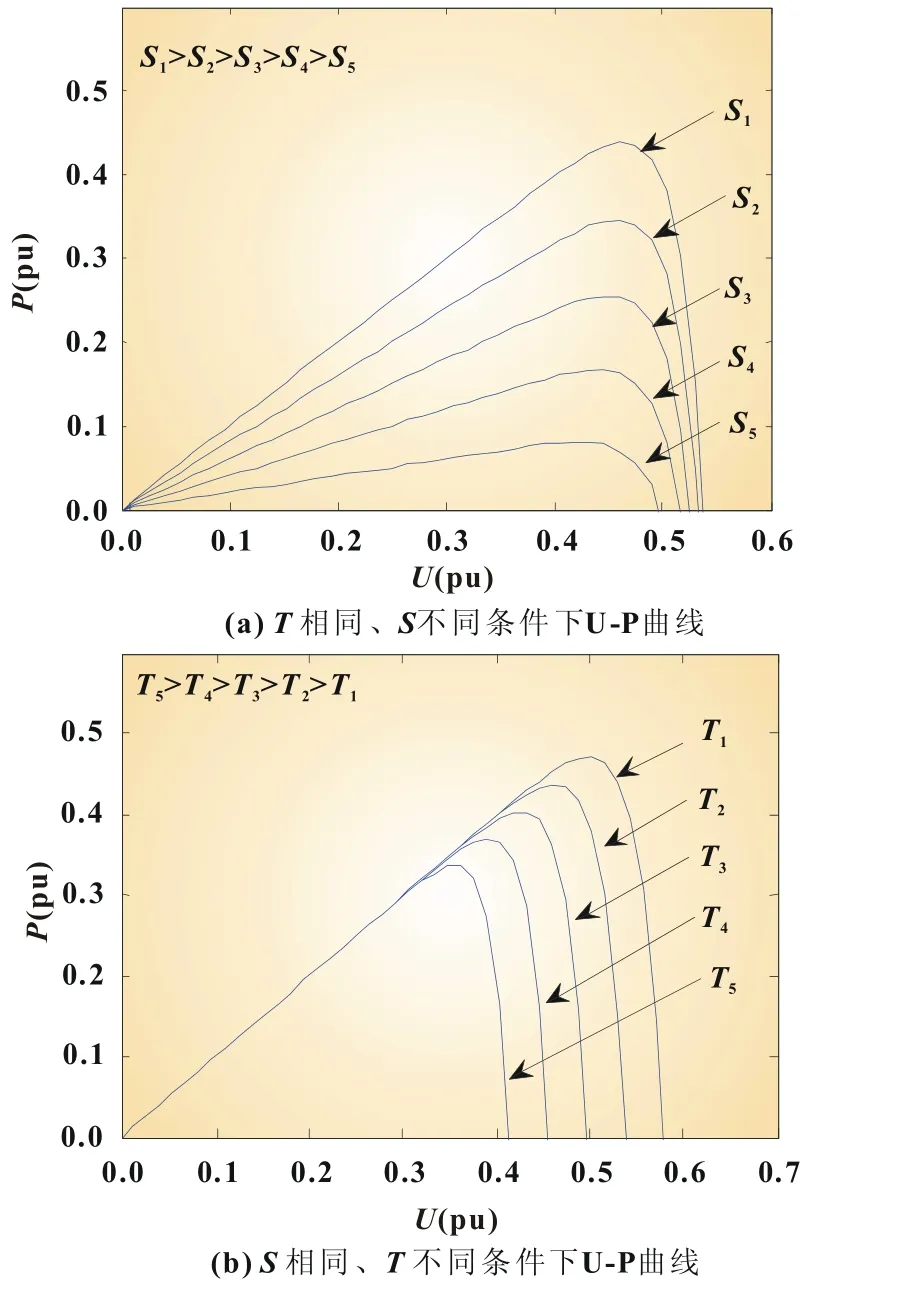
图2 不同条件下U-P曲线

在实际光伏发电系统中，光伏阵列的输出功率往往同时受到环境温度及太阳辐照强度变化的共同影响。总体而言，光伏阵列的输出功率随着温度的增加而产生减小的趋势，光伏阵列的输出功率随着太阳辐照强度的增加而产生增大的趋势，因此光伏阵列的实际输出功率正是这两种趋势相互作用的结果。

2 基于果蝇优化算法的MPPT

2.1 果蝇优化算法(FOA)全局搜索

果蝇优化算法(FOA)是一种基于果蝇觅食行为而推演出的寻求全局最优化的新方法。果蝇具有非常发达的嗅觉器官，能凭借空气中的气味便可获得食物源的方向，同时在飞近食物位置后亦可使用敏锐的视觉发现食物与同伴聚集的位置，并且往该方向飞去，最后寻找到食物。因此，FOA可具有方法简单、运行速度快、收敛稳定等优点[8]。

果蝇群体搜索全局最优的步骤如下：

步骤1：随机初始果蝇群体位置，如图3所示。

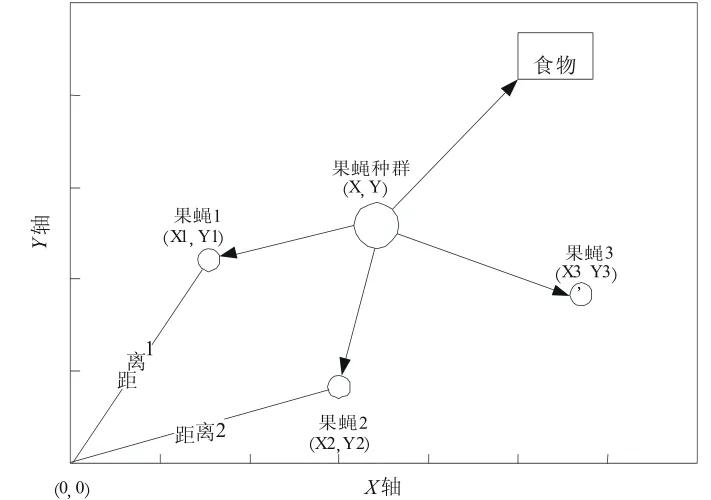
图3 果蝇群体迭代搜索食物示意图

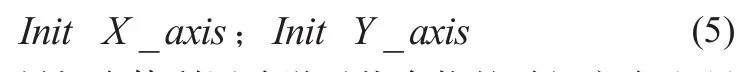
步骤2：给定果蝇个体利用嗅觉寻找食物的随机方向和距离。

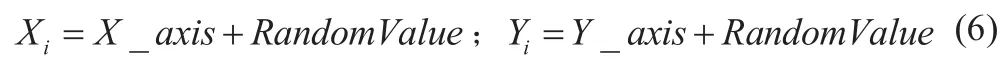
步骤3：由于无法得知食物的具体位置，因此先计算该点与原点的距离()，再计算味道浓度判定值()，此值为距离的倒数。

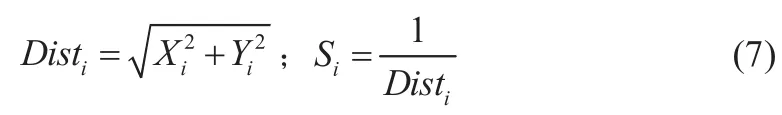
步骤5：找出此果蝇群体中的味道浓度最高的果蝇(求极大值)。

步骤7：进入迭代寻优，重复执行步骤2～步骤5，并判断味道浓度值是否优于前一次迭代味道浓度值，若是，则执行步骤6。

2.2 果蝇优化算法(FOA)应用于光伏阵列MPPT中

果蝇优化算法是群体智能的一种新方法，既属于演化式计算的范畴，也属于人工智能的领域。将果蝇优化算法应用于光伏阵列最大功率点跟踪控制中，整个算法过程分为两个部分：一部分为果蝇的寻优环节，另一部分为MPPT寻优部分。在FOA优化算法中，每个优化问题的潜在解(即最大功率点)都是搜索空间中的一个“果蝇”，所有果蝇个体都有一个被目标函数决定的适应值。本文定义光伏阵列的总输出功率为目标函数。其具体步骤如下：

(1)算法的初始化

设置初始果蝇群体的位置、种群数量、迭代次数和迭代步进值。

(2)种群评价

在对各种参数进行初始化后，计算每个果蝇对应目标函数的适应值。目标函数为光伏阵列输出的总功率，适应度函数的表达式为：

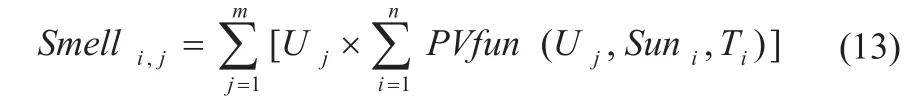
式中：PVfun为光伏阵列的输出特性函数。

通过调用一个适应度函数计算功率值的大小，该函数实质上包含了每个模块的电流、电压公式并将它们进行加权和形成总的系统功率输出。

(3)比较确定个体和全局适应度及极值

比较单个果蝇当前适应度值和历史最好适应值两者间的大小，如果是当前适应值较大，那么更新果蝇的适应度值。每个果蝇的最好适应度功率值都确定后，相互比较以确定全局的最优适应度值。

(4)更新果蝇的位置

(5)检查结束条件，若满足，结束寻优，输出最优解的范围；否则转至步骤(2)，当达到最大进化代数时即终止寻优过程。

基于FOA优化算法的MPPT控制流程如图4所示。

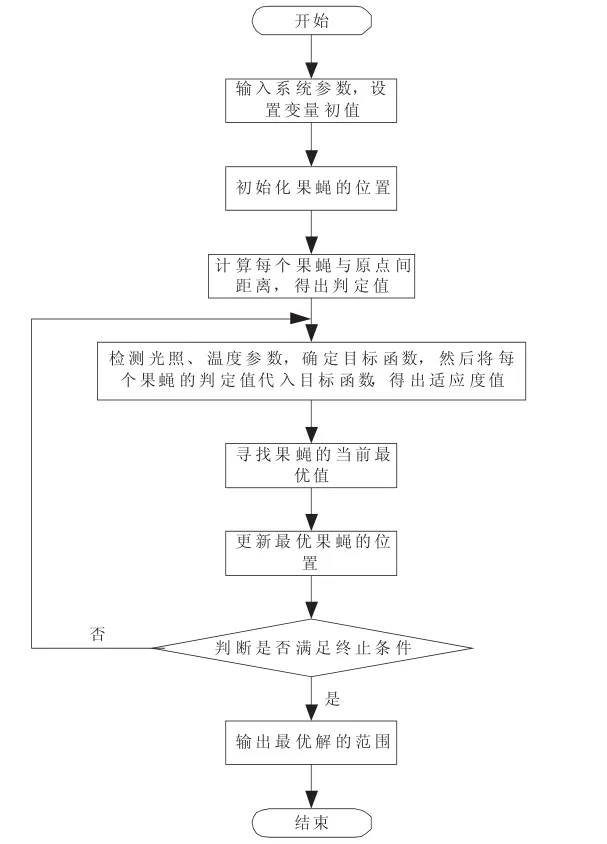
图4 基于果蝇最优化算法的全局搜索流程

3 仿真及其分析

根据上述公式，在Matlab/Simulink环境下建立光伏仿真模型[9](图5)。其中光伏阵列的常数模块通常采用供应商所提供的重要参数值，此处设置=316.4 V、=256.2 V、=22.5 A、=20.8 A、=0.2 Ω、=0.015、=0.7、=25℃、= 1 000 W/m2。本文分别采用P&O、InC和FOA三种算法进行对比仿真研究，仿真波形图分别如图6、图7、图8所示。

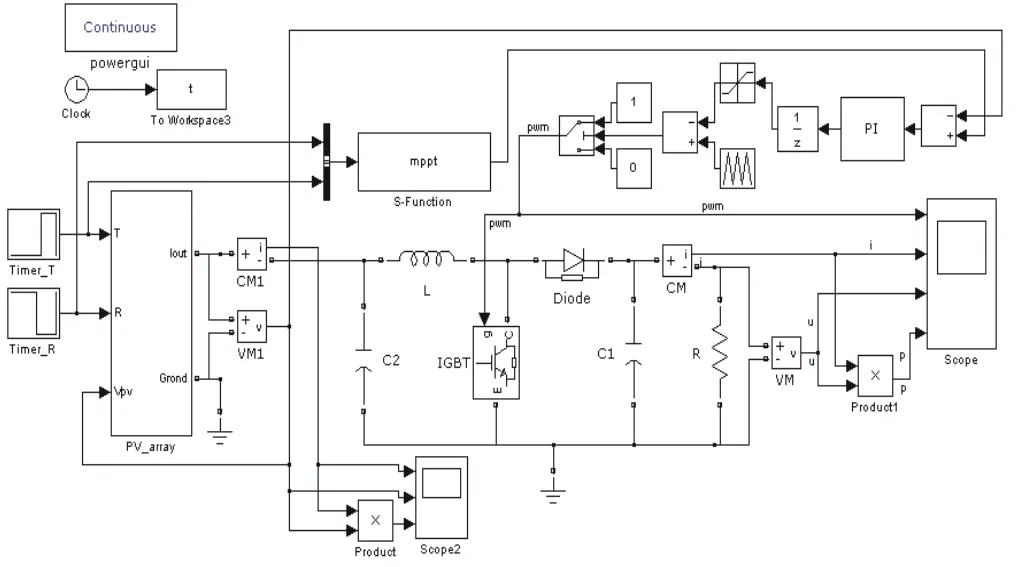
图5 光伏阵列MPPT仿真模型图

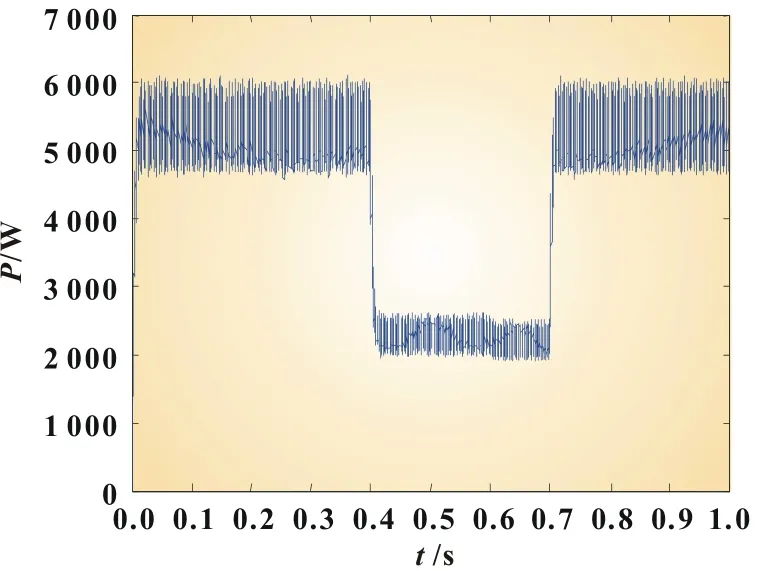
图6 基于P&O的MPPT过程

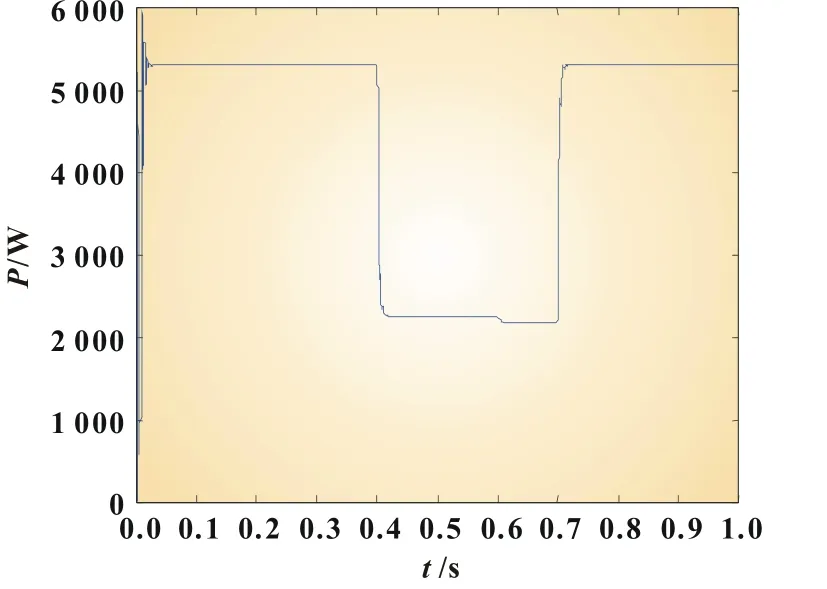
图7 基于InC的MPPT过程

图5中，MPPT统一采用S函数编写程序[10]。通过太阳辐照强度和环境温度的变化来比较几种方法对功率的跟踪效果。设置环境温度Time_T，在0～0.4 s内，温度恒定为25℃；在0.4～0.6 s内，温度升为60℃；在0.6～1 s内，温度降为25℃。设置太阳辐照强度Time_S，在0～0.4 s内，太阳辐照强度恒为1 000 W/m2；在0.4～0.7 s内，太阳辐照强度降为600 W/m2；在0.7～1 s内，太阳辐照强度升至1 000 W/m2。

图6、图7分别为采用P&O法和InC法的MPPT的跟踪过程。可以看出，输出功率随着温度的升高而略有降低，输出功率随着光照强度的升高而显著升高，反之亦然。因此，在0.4 s时、0.6 s时和0.7 s时分别存有不同的MPP。P&O法在光伏阵列MPP处一直存有振荡现象，最终来回往复稳定在MPP附近的一个范围内。InC法能够明显改善P&O法的不足，并最终稳定在MPP处，但是此法在初始搜索跟踪时存有较大波动误差，而且当外界因素发生变化时，都需要经历一定的功率波动后方能稳定在MPP处。

由图8可知，FOA算法的跟踪速度很快，对外界因素的变化有较强的适应性且稳态误差小，动、静态性能良好。与前两种跟踪算法相比，FOA算法的MPPT效果明显。而且由图9可见，算法只需要较少的迭代次数就能稳定在MPP处，具有很明显的优势。图10为果蝇寻优路径。

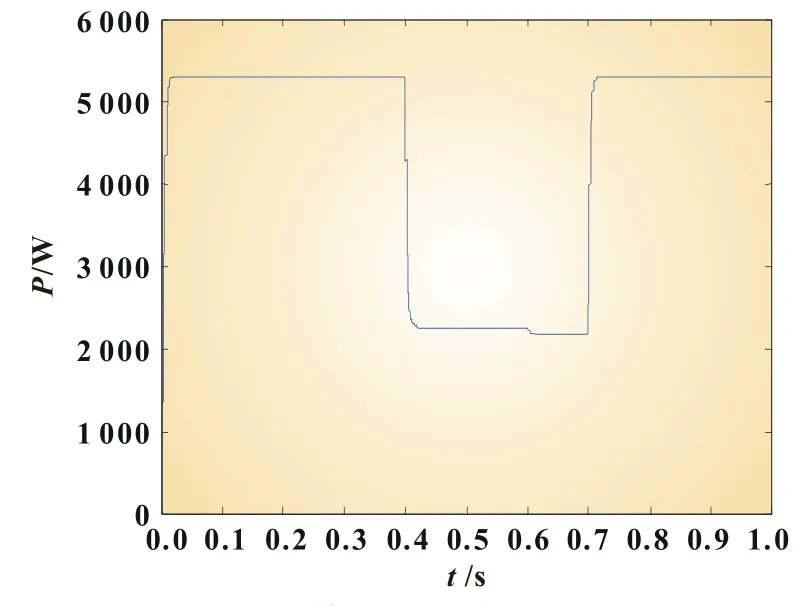
图8 基于FOA的MPPT过程

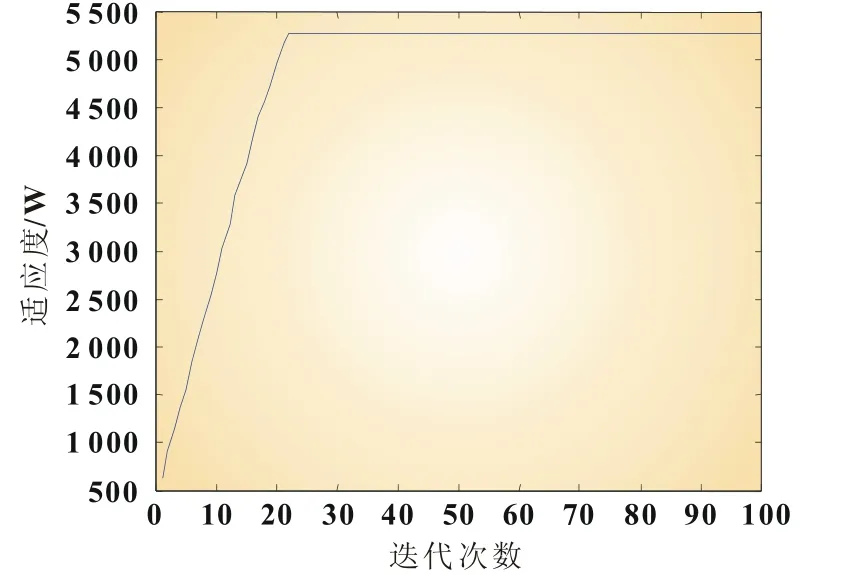
图9 迭代化过程

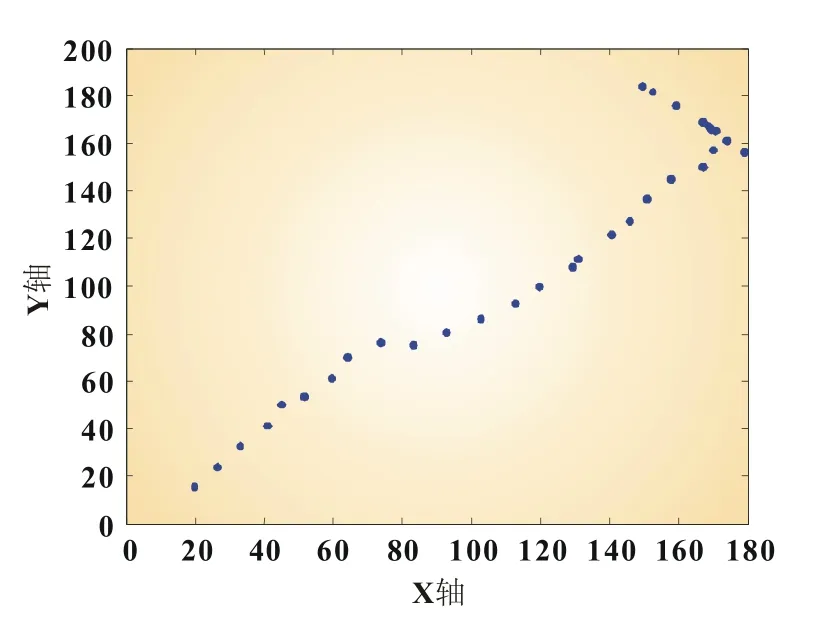
图10 果蝇寻优路径

4 结论

将FOA算法应用于光伏阵列的MPPT中，运用仿真软件Matlab/Simulink建立整体系统仿真模型，分别将三种算法对光伏阵列进行仿真，并比较了输出功率的跟踪效果。结果充分说明了FOA算法能够快速准确地跟踪光伏阵列的MPP，减少系统在最大功率点振荡的能量损失，提高了光伏阵列的输出效率。

[1]茆美琴，余世杰，苏建徽.带有MPPT功能的光伏阵列Matlab通用仿真模型[J].系统仿真学报，2005,17(5):1248-1251.

[2]黄舒予，牟龙华，石林.自适应变步长MPPT[J].电力系统及其自动化学报，2011(5):26-30.

[3]杨永恒，周克亮.光伏阵列建模及MPPT控制策略[J].电工技术学报，2011,26:229-234.

[4]王雨，胡仁杰.基于MATLAB的光伏模块输出特性及MPPT的建模与仿真[J].半导体光电，2012,33(1):18-21.

[5]何人望，邱万英，吴训，等.基于PSIM的新型扰动观察法的MPPT仿真研究[J].电力系统保护与控制，2012,40(7):56-59.

[6]邵卫超，朱凌.基于MATLAB的光伏阵列阵列MPPT仿真研究[J].电源技术，2012,36(2):209-211.

[7]王志敏，张建军，郭燕琼.一种改进的光伏发电系统MPPT控制方法[J].西安石油大学学报，2012,27(2):89-92.

[8]潘文超.应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J].太原理工大学学报，2011,29(4):1-5.

[9]王建华，韩伟.光伏阵列的仿真研究[J].信息技术，2011，6:122-126.

[10]邓栋，易灵芝，李明，等.基于S-函数光伏阵列最大功率跟踪的控制策略[J].湖南工业大学学报，2009,23(5):52-54.

Simulation study of photovoltaic power generation in maximum power point tracking based on FOA

In order to increase the output power of the photovoltaic system,the maximum power point tracking was needed. As the starting point of research in the output nonlinear characteristics, based on the analysis of the advantages and disadvantages of the conventional algorithm, and aiming at the poor dynamic and steady-state performance of the maximum power point tracking(MPPT),the fly optimization algorithm(FOA)was applied to the photovoltaic power generation system.Modeling and simulation in MATLAB/Simulink,the results indicate that the method can quickly and accurately track the maximum power point of photovoltaic cells and prevent the occurrence of the algorithm to track the direction of misjudgment of the situation, and show good dynamic and steady state characteristics,also confirm the correctness and validity of the algorithm.

fly optimization algorithm;photovoltaic power generation;maximum power point tracking(MPPT);fitness function

TM 615

A

1002-087 X(2015)10-2193-03

2015-03-09

江苏省研究生培养创新工程(CXZZ12_0228)；江苏省科技支撑项目(BE2012015)

杜炜(1981—)，男，河南省人，博士，工程师，主要研究方向为现代电力电子技术、太阳能发电技术。

韩伟(1986—)，男，江苏省人，博士生，主要研究方向为分布式发电与微网。E-mail：hanwei860610@126.com。