基于输入限制的I-ELM机车热轴等级判别模型

宋平岗，林家通，康水华，杨云

(华东交通大学 电气与电子工程学院，南昌 330013)

滚动轴承是机车走行部的关键零件，其状况直接影响机车的性能与安全[1]。高速运行中，如果轴承发生故障甚至卡死，会产生热轴现象，不能及时处理将造成切轴甚至颠覆事故[2]。据统计，80%以上的火车翻车事故由热轴造成。

目前，广泛采用红外线轴温探测系统(Trace Hotbox Detection System, THDS)监控热轴现象，但其实际应用中预报兑现率普遍较低，误报率较高[3-5]。由于热轴判别的复杂性，目前THDS设备根据历史经验设定热轴判别阈值，无法直接满足实际应用要求。为提高温度判别准确率，文献[6]提出使用模型算法对轴温建立识别模型，实现对轴承温度的模糊判别，但其存在隶属度函数设计困难，参数设计主观性强等不足。文献[7]提出了基于模糊神经网络的热轴判别模型，准确率较高,但存在神经训练层及隐含神经元多，计算速度慢等缺陷。

针对上述问题，引入增量型极限学习机(Incremental Extreme Learning Machine, I-ELM)算法，该算法具有学习速度快、参数少、精度高等优势[8-10]。I-ELM算法随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值，且在训练过程中无需调整，只需设置隐含层神经元的个数便可获得唯一的最优解，通过不断增加隐含层神经元个数减小训练误差，提高网络精度。针对机车轴温的非线性复杂多变特性，提出带输入限制的极限学习机，对热轴级别进行判别，并将其应用于和谐型机车轴承温度监测报警装置中。

1 机车热轴判别模型

1.1 背景分析

轴承内部的摩擦是其主要热源。从生热的角度考虑，整体生热法和局部生热法以实验室测量结果为基础，总结出的经验公式并不能完全适用于机车轴承复杂温度场情况。热网络法和有限元法采用理论分析，事先假设了某些特定条件，结论形式复杂且计算量大，无法满足机车轴温故障快速报警的要求[11]。

机车轴承运行温度的影响因素多而复杂，且相互交叉关联。THDS设备在实际中判别效果并不理想，主要因为机车运行在不同区间时，温度、气候等环境因素存在较大变化，且车型、车种，轴承结构、运行速度、负载情况等内在因素差异都直接影响机车轴承的运行温度。这些复杂且密切关联的因素决定了机车轴承温度模型的复杂性。

目前，THDS设备生产厂家常根据历史经验设定热轴判别的阈值。由于机车的运行环境及自身运行情况存在变化，固定的阈值无法适应实际应用需求。因此，热轴级别判断没有固定的公式与模型，可以视作其中内在关联因素发生作用，直接体现在轴承温度上。在此，分析轴承温度与其热轴级别，并采用神经网络训练的中间隐含层表述其内在关系。

1.2 机车热轴判别模型

极限学习机(Extreme Learning Machine，ELM)是典型的单隐含层前馈神经网络结构，由输入层、隐含层和输出层组成，输入层与隐含层、隐含层与输出层神经元之间全连接。

热轴判别受诸多因素影响，一般不直接使用轴温作为热轴判别指标，而是使用轴温温升[5-7]。轴温温升是指轴温与环境温度之差，选取温升T1、列温升T2、辆温升T3作为模型的输入，其具体含义见表1。

表1 模型输入含义

模型的输出为热轴等级G，沿用铁路系统做法将热轴等级分为正常、微热、强热、激热共4级，分别用1，2，3，4表示输出。则ELM神经网络结构如图1所示。

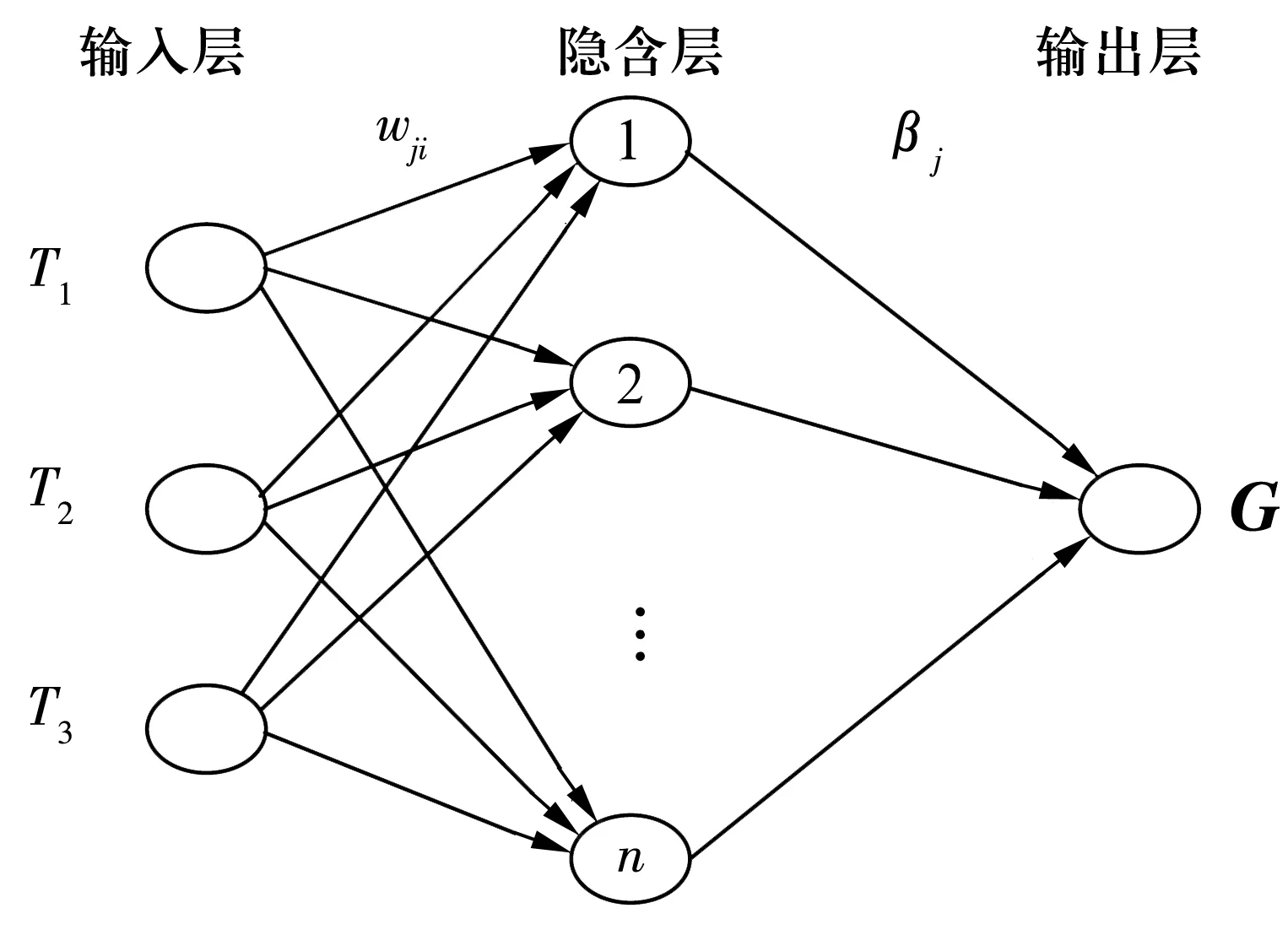
图1 ELM神经网络结构

设隐含层神经元为n，则输入层与隐含层之间的连接权值w为

(1)

式中：wji为输出第i个神经元与隐含层第j个神经元间的连接权值,j=1,2,…,n;i=1,2,3。

隐含层与输出层间的连接权值β为

β=[β1,β2,…,βn]T，

(2)

式中：βj为第j个神经元与输出神经元的连接权值。

隐含层神经元的阈值b为

b=[b1,b2,…,bn]T。

(3)

设隐含层激活函数为g(x)，则具有Q个训练样本的神经网络输出G可以表示为

(4)

其中wi=[w11,w12,w13]，(4)式可以进一步表示为

Hβ=GT，

(5)

H(w1,w2,…,wn,b1,b2,…,bn,T1,T2,…,TQ)=

(6)

若给定满足某些条件的激活函数，如sigmoid，sine，hardlim和RBF函数，则神经网络的输出可以任意精度逼近目标函数[12-13]。因此,在极限学习机算法中，连接权值w和阈值b在训练中随机选择且在训练中保持不变。而隐含层与输出层间的连接权值β可以通过求解以下方程组的最小二乘解获得

(7)

其解为

(8)

式中：H+为隐含层输出矩阵H的Moore-penrose广义逆矩阵。

1.3 隐含层神经元数目确定

隐含层神经元数目太少或太多对神经网络的性能都有影响，而随着隐含层神经元数目的增加，增量型极限学习机的输出误差趋势逐渐减小并趋近零[14]，即第k+1次迭代所获取的网络输出误差小于第k次迭代，不会出现过拟合问题。

因此，选取隐含层神经网络具体做法是：首先给定隐含层神经元初值n，训练误差η，如果网络输出误差E大于训练误差η，则增加隐含层神经元数目，重新训练网络，直至E<η。

1.4 基于输入限制的I-ELM热轴等级判别模型

根据电力机车轴温的特性，通常THDS设备在轴承温升达到40 ℃时预报微热，温升超过70 ℃时预报激热[6]。但是简单的“一刀切”往往会造成判断错误，故采用I-ELM热轴等级判别模型。在轴承温升低于30 ℃时，可以不通过ELM算法即可明确判定为正常运转温度；同样，温度超过100 ℃的强烈发热的情况下，可以直接判定为激热。判别表达式为

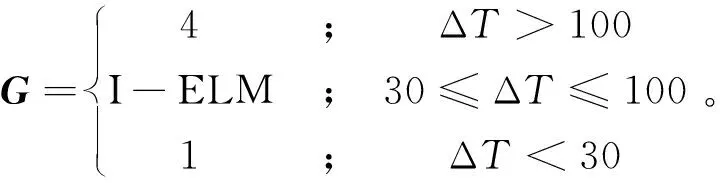
(9)

通过温升能够直接判断热轴等级的数据，减小ELM的计算量，从而提高算法的效率。因此，基于输入限制的I-ELM热轴等级判别模型实现步骤为：

1)处理数据并获取Q个训练样本，给定训练误差η；

2)设隐含层神经元数目初值n=0, 样本训练误差E；

3)设隐含层节点n=n+1；

4)随机产生输入层与隐含层之间的连接权值w及隐含层神经元的阈值b；

5)选择sigmoid函数为激发函数，并根据(6)式计算隐含层输出矩阵H；

6)根据(8)式计算隐含层与输出层间的连接权值β；

7)根据(4)式计算神经网络的输出G；

8)计算训练样本误差E

(10)

若E<η，则终止训练，否则跳至第3)步；

9)限制输入，筛选测试样本。温升低于30 ℃时热轴等级为1，温升大于100 ℃时热轴等级为4。筛选后组成新的测试样本；

10)测试训练网络。将新的测试样本输入训练好的网络，将预测值与测试样本实际输出值进行对比，检验模型判别能力。

2 仿真分析

仿真试验基于MATLAB7.8平台，共选取60个样本，其中正常、激热、强热样本各10个，微热样本30个。为达到较好的训练网络，每个热轴等级的样本数据按照训练样本与测试样本4∶1的比例选取，即训练样本48个，测试样本12个。首先设定隐含层神经元初值L为30，训练允许误差E为4%，进行隐含层神经元个数选取，结果见表2。

表2 不同隐含层神经元个数的误差

由表2可知，随着隐含层数目的增加，误差E有波动，但总体趋势是误差越来越小。当L=44时，误差E=2.08%，符合要求，因此将隐含层神经元数目固定为44。将训练好的网络用于测试样本,预测结果与真实值的对比如图2所示，分类正确率达91.667%，其中热轴等级为正常运转、微热和激热分类正确率为100%。由于样本数较小，神经网络的训练精度较差。如果强热样本数再多一些，分类正确率还会有所提高。

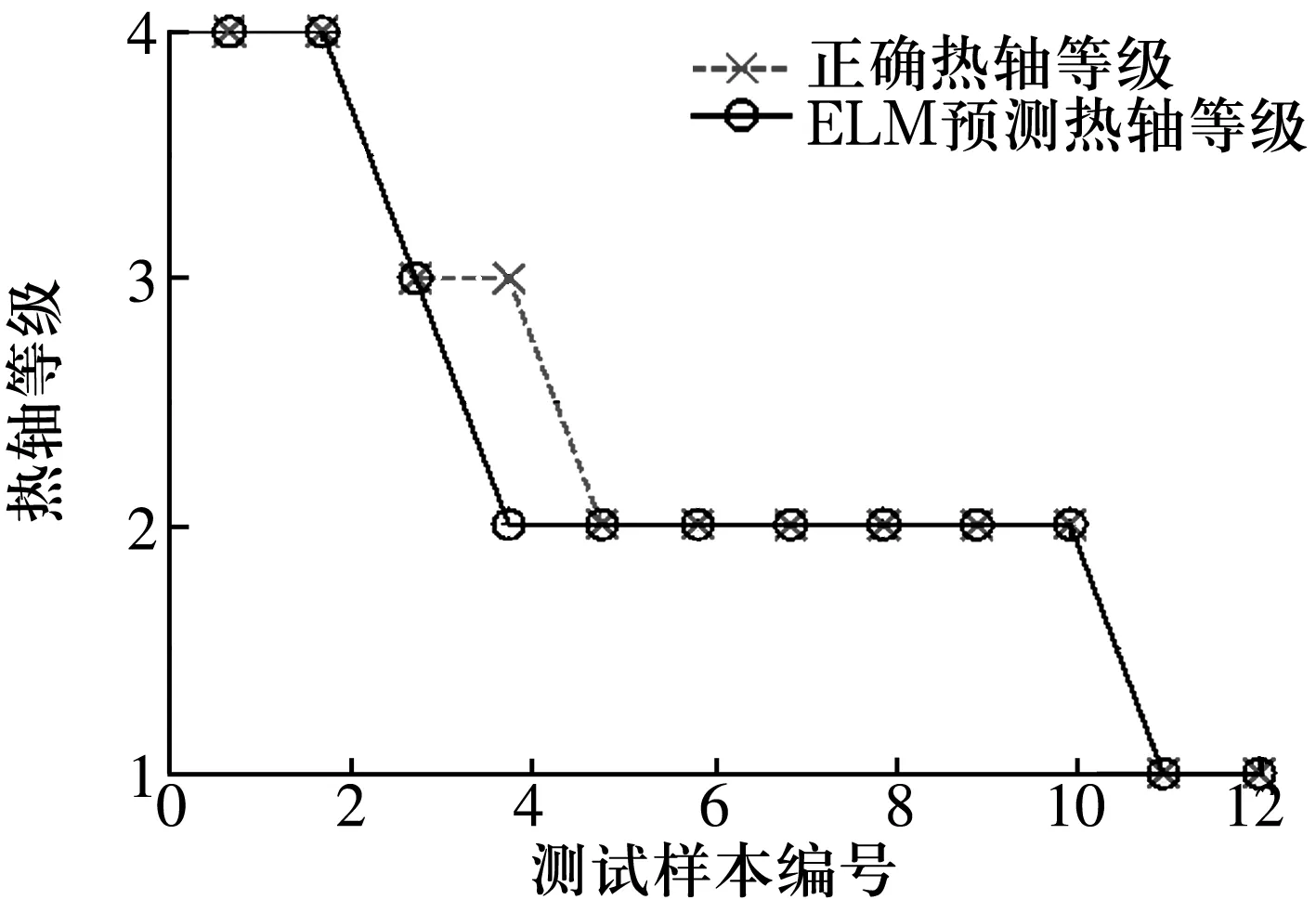
图2 ELM模型热轴等级判别结果

为进一步验证模型的有效性，采用传统的BP神经网络和RBF神经网络进行分析，结果如图3和图4所示。3种模型运行时间和判别准确率的对比结果见表3，ELM的效率及准确率均高于其他2种模型。

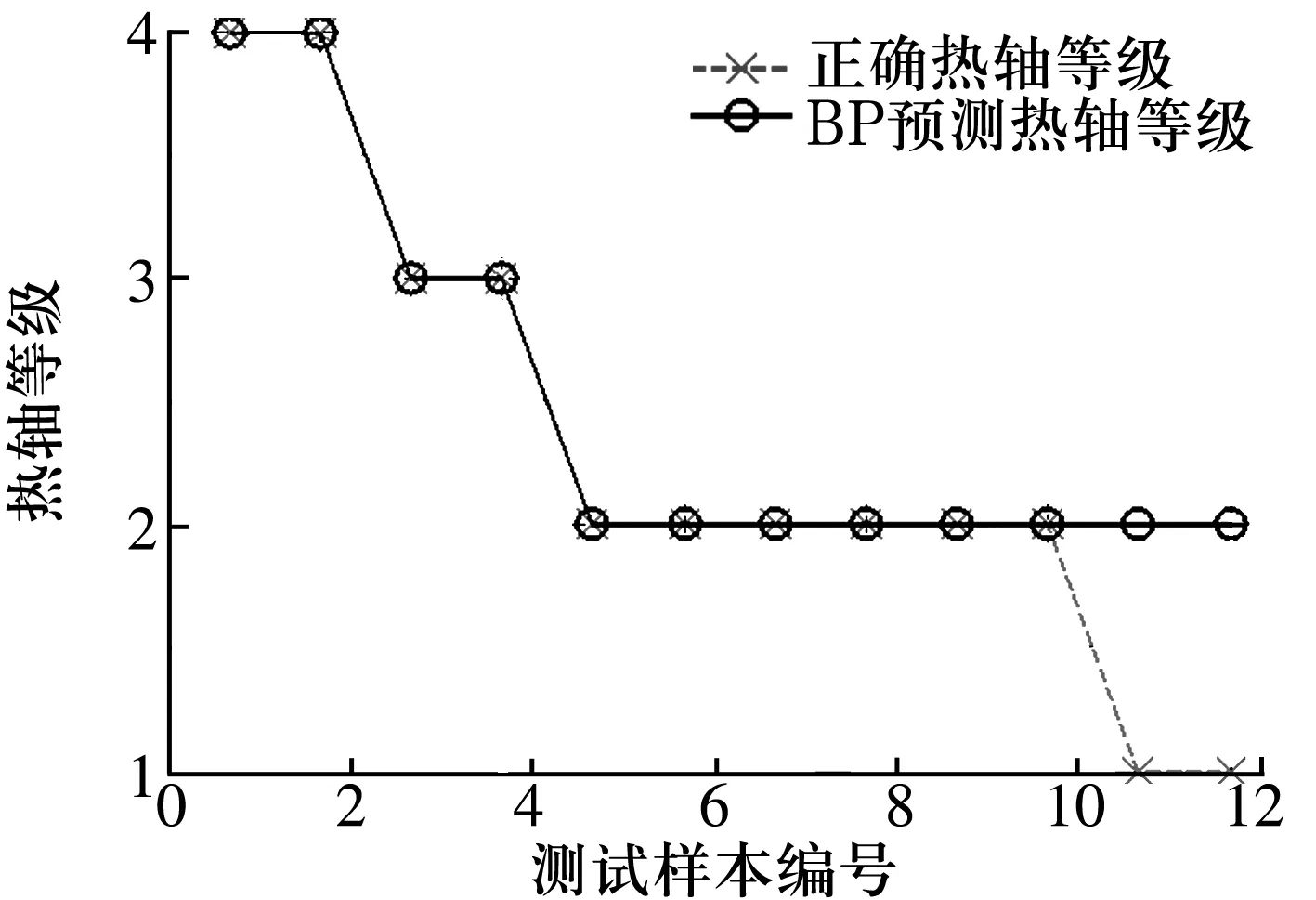
图3 BP模型热轴等级判别结果

图4 RBF模型热轴等级判别结果

表3 算法运行时间

3 算法应用

根据上述模型，设计了和谐型机车轴承温度监测报警装置，其系统结构如图5所示，由传感器、接线盒、通信总线、主机和显示器等组成。系统采用1-wire总线数字温度传感器，每个传感器采用吸附式安装方式固定到每个温度测量点[15]。传感器安装部位如图6所示，每个轴位测量电动机大、小端，车轴左、右端，抱轴左、右端等6个轴温测量点，每个轴位还可接1个环境温度探头，即每个主机上布置28个温度探头。

图5 系统整体结构框图

图6 系统温度传感器安装实物图

采用Contex-M3处理芯片ARM5749作为主控处理器。主机测量的温度数据经ARM5749计算处理后在显示器上显示，同时通过色块警示及蜂鸣器报警，温度显示与报警效果如图7所示。

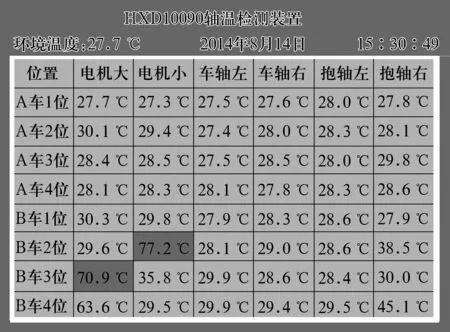
图7 系统温度显示及报警界面

在系统设计中，系统需要完成传感器温度值的采集、计算、分析、数据处理、报警等级识别及液晶显示驱动等。在程序设计中根据经验选取40个输入、输出样本作为固定的训练参数，并根据测量诊断结果自动增加或更新20个输入、输出结果作为实时变化的训练参数。具体ELM算法流程如图8所示。

图8 系统整体结构框图

4 结束语

将ELM模型应用于机车热轴级别判别，并结合热轴自身特性提出了基于输入限制I-ELM判别方法。根据设计精度要求选定隐含层神经元数目，针对多数的常规低温升情况与少量特高温升故障情况，不输入ELM网络而直接判别，极大提高了模型的判别效率。

仿真结果表明，ELM热轴等级判别模型不仅判别准确性有所提高，而且大大缩短了运行时间。多年实际应用表明，热轴等级模型判别准确，运行效果良好。