保持架兜孔形状对高速球轴承动态摩擦力矩的影响
徐俊,杨雷,李娟,于晓凯,尹延经
(1.洛阳轴研科技股份有限公司,河南 洛阳 471039;2.驻中国空空导弹研究院军事代表室,河南 洛阳 471039)
轴承保持架的几何特性以及由此引起的不稳定性一直是高速精密球轴承设计中必须考虑的重要因素之一。通常在设计保持架时,必须考虑内外径的同心度、保持架壁厚、兜孔间的尺寸差、兜孔几何形状和兜孔尺寸等参数。下文主要分析保持架兜孔几何形状对高速精密球轴承动态摩擦力矩的影响。
1 高速球轴承保持架结构
目前高速精密球轴承普遍采用工程塑料实体保持架,其结构形式如图1所示。保持架兜孔几何形状大多为圆形和方形,加工方法主要是采用车加工。

图1 实体保持架兜孔几何形状
2 理论分析
在高速精密球轴承中保持架是一个自由体,在外力的引导下产生回转运动,当其与套圈作相对运转时,如果是同心运动,在各个方向上所受的力可能是相等的,即保持架在一个平衡外力作用下仍保持平衡,但实际上由于球体作用于保持架上的力以及保持架自身质量的不均匀性,使保持架所受的外力不可能为一个平衡力,将导致保持架产生偏心运动,即常见的涡动。偏心涡动越大,轴承工作时的内在功率损耗越大,即轴承摩擦力矩越大[1]。
在高速精密球轴承中球体和保持架之间发生弹性接触,保持架兜孔与球体法向作用力Qcj的计算式为[2]
(1)
式中:zcj为第j个兜孔中心位置与其对应的钢球中心的位移;Kc为试验数据确定的线性逼近常数,对于球轴承取Kc=11/Cp;Cp为保持架兜孔间隙,Cp=0.5(Dp-Dw);Dp为保持架兜孔名义直径;Dw为钢球直径;Kn为球与保持架兜孔接触处的载荷-变形常数,其值可取为
(2)
k=1.033 9(Rη/Rξ)0.636 0,
(3)
R=RξRη/(Rξ+Rη),
(4)
(5)
Rη=0.5Dw,
(6)
ε=1.000 3+0.596 8Rξ/Rη,
(7)
Γ=1.527 7+0.602 3ln(Rη/Rξ) 。
(8)
分析以上各式可知,方兜孔与圆兜孔相比,各种参数存在如下关系:1)当Rξ减小时,系数k,R,Γ均减小;2)当ε减小时,Kn,Qcj均减小。
由于保持架是一个能量耗散零件,其运动能量全部来自于套圈和球体,当高速精密球轴承保持架为稳定状态时,保持架与套圈不存在“啸叫”现象[3],球作用于保持架的力越小,轴承的动态摩擦力矩越小。
3 试验验证
为了验证上述理论的正确性,选用7004AC TN3/HV P4轴承进行试验。试验轴承采用背靠背安装(图2),引导方式为外圈引导,试验转速为5 000 r/min,采用保持架含油润滑方式润滑。
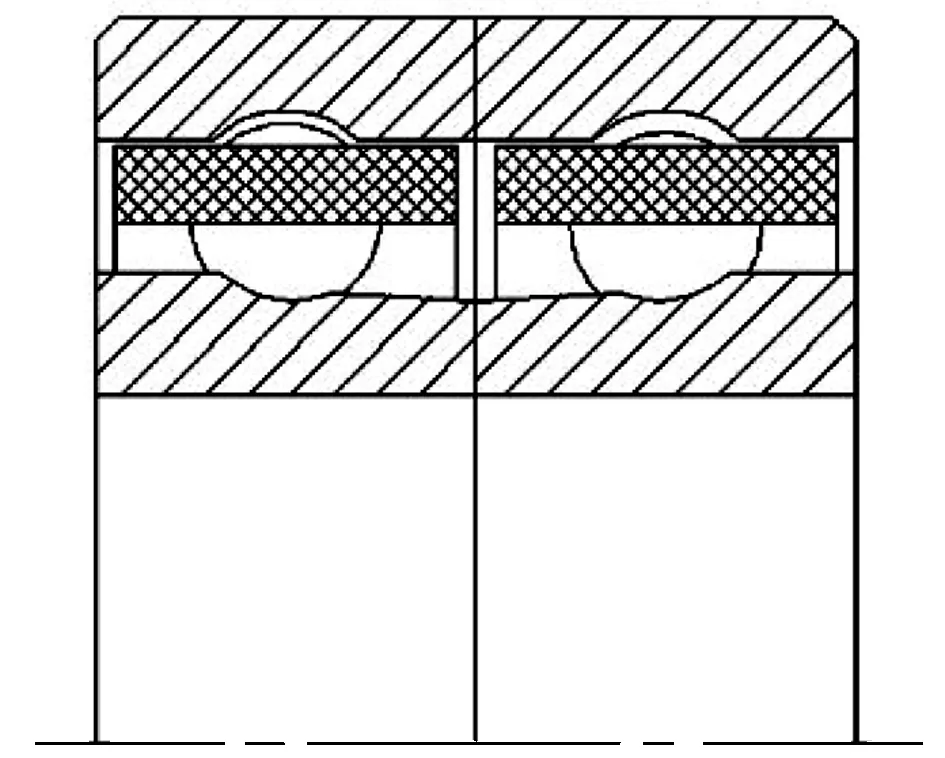
图2 高速精密球轴承安装示意图
为消除其他因素对试验结果的影响,假设预紧力、兜孔间隙、含油率等参数均不变,分别对编号为1#和2#的2组电动机轴承进行试验。先将圆兜孔保持架装入电动机轴承中进行150 h常温运转试验,再将方兜孔保持架装入同一台电动机轴承中,同样进行150 h常温运转试验。试验后1#,2#电动机轴承基本性能参数见表1,动态摩擦力矩曲线如图3、图4所示。
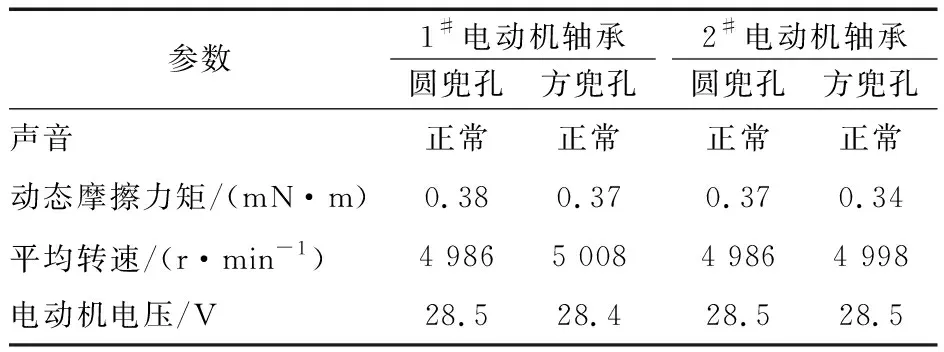
表1 不同兜孔时1#,2#电动机轴承性能参数对比

图3 不同兜孔时1#电动机轴承动态摩擦力矩曲线
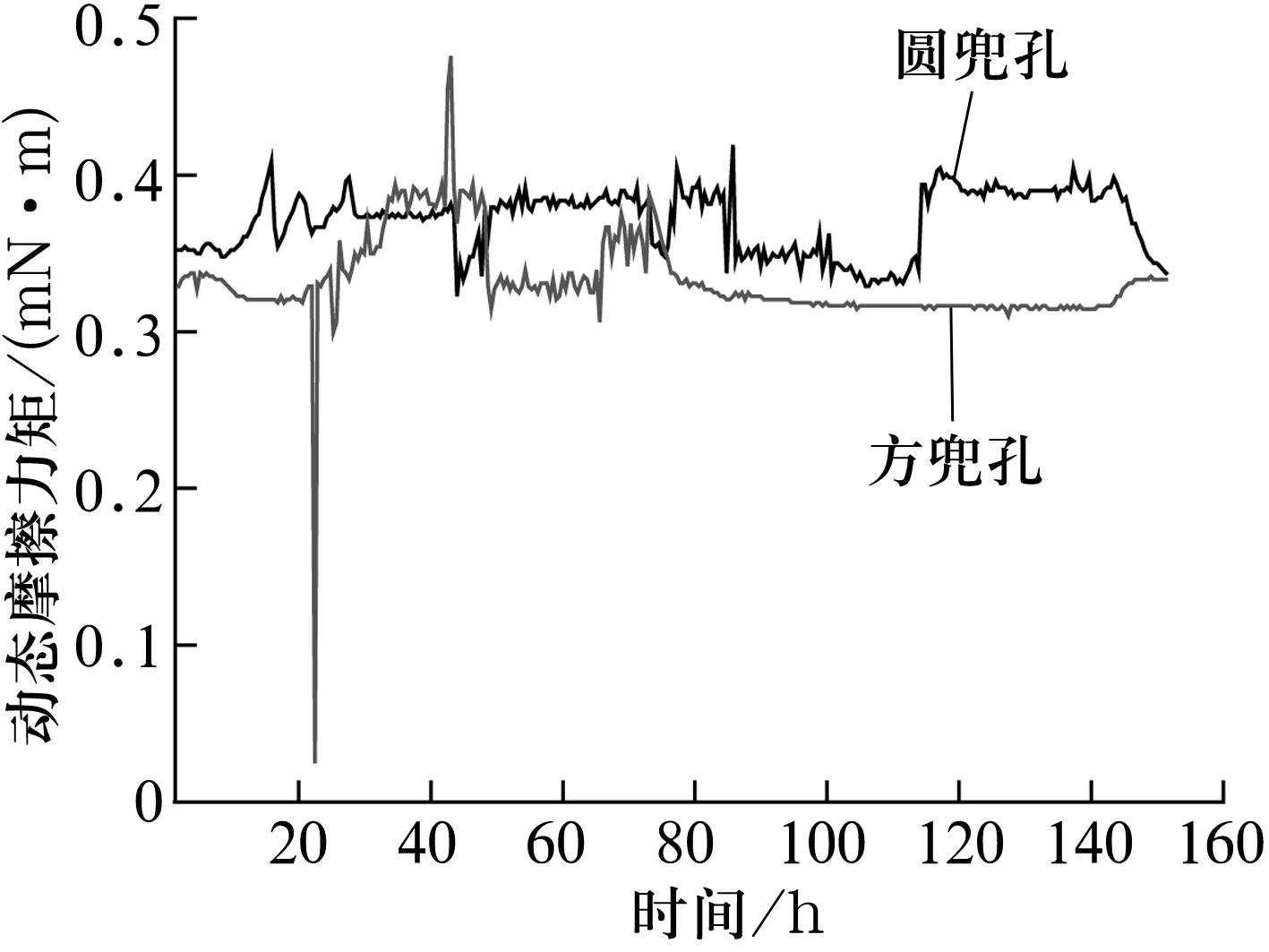
图4 不同兜孔时2#电动机轴承动态摩擦力矩曲线
由表1可知,2种兜孔保持架的轴承声音均正常,与圆兜孔相比,采用方兜孔保持架时电动机轴承动态摩擦力矩更小。
由图3、图4可知,采用方兜孔保持架时,初始阶段轴承摩擦力矩值较大且波动较大,但随着时间的推移,轴承摩擦力矩急剧减小,且波动很小。分析认为,初始阶段轴承动态摩擦力矩波动较大可能是由保持架机械加工毛刺、保持架出油率不稳定等因素所致,经过跑合后,轴承动态摩擦力矩变小并逐渐保持在相对稳定的状态。
试验后分别对2台电动机轴承进行分解,对保持架进行分析,其形貌如图5、图6所示。

图5 试验后1#电动机轴承保持架分解图

图6 试验后2#电动机轴承保持架分解图
由图5、图6可知,保持架兜孔均有明显的摩擦接触痕迹,在其他条件不变的情况下,更换方兜孔保持架后,保持架兜孔与钢球的接触痕迹小而均匀,组件的电流变化更加平稳,保持架磨损得以改善。
4 结束语
试验结果表明,在相同工况条件下,与圆兜孔保持架相比,采用方兜孔保持架时轴承的动态摩擦力矩较小且稳定。文中是在常温状态下进行的验证试验,在其他温度环境下采用方兜孔保持架轴承的动态摩擦力矩是否依然较小,还有待进一步探讨。

