一种基于神经网络同步的密钥协商算法

李 涟，邹苏真

(1.重庆理工大学计算机科学与工程学院，重庆 400054;2.中国联通重庆市分公司，重庆 400054)

公共密钥交换协议(PKEPs)由Diffie和Hellman提出并在现代密码学中扮演着重要的角色。基于数论的PKEPs现已被广泛研究［1］。然而，人们发现神经同步也能实现同样的目标，被称之为神经密码学。神经密码学背后的这种机制类似于“通过协商的密钥协议”［2］。神经密码计算量小且为小型嵌入式系统的结构，目前已受到重点关注。

神经密码需要通信双方拥有相同的网络结构，通过在线学习获得同步。在同步过程的开始阶段，两个神经网络随机选择各自的离散权值，它们是要求保密的。在每一次学习步骤中，通信双方A和B获得相同的输入值并交换它们的输出值。如果A和B同意这个输出值，它们各自内部的权值会通过一定的学习规则来进行调整，在有限的学习步骤内达到完全同步。这个相同的权重可以作为它们共同的密钥。显然，A，B之间的权重更新受输出值影响，因此，这种同步方式称为双向同步。另一方面，攻击者E可以通过A或B的输入和输出值组成的例子来与之同步。注意，E无法影响A，B的权重更新，E的同步方式为单向同步。人们发现双向同步和单向同步的平均步长数是相同的［3］，为了保证神经密钥交换的安全性，单向学习与共同学习速度必须是不同的。通过观察TCM和TPM密钥协商算法［4］的同步效率，研究者发现，使用TPM算法的双向学习的平均同步步数和突触深度L呈多项式增长，然而，单向学习的同步平均步数和突触深度呈指数增长［5］。换言之，随着突触深度L的增长，TPM算法双向同步的速度要远高于单向同步。因此，TPM算法可以通过调整模型内部的突触深度来抵御各种安全攻击。然而，TCM算法中双向同步与单向同步的平均时间和突触深度L呈指数增长，因此，TCM算法的安全性是较弱的。目前，4种神经网络攻击算法包括简单攻击［2］、几何攻击［6］、大多数攻击和遗传攻击［7－8］，已得到广泛的应用。大多数攻击和遗传攻击以前面两种攻击为基础。由于自身安全性的缺陷，TCM算法无法抵御较高级的安全攻击。

1 TCM模型与密钥建立算法

1.1 TCM 模型

图1中，1个TCM神经元有K个隐藏单元、K×N个输入神经元和1个总输出神经元。每个隐藏单元的功能相当于1个独立的感知器，并且它内部的元素权重都为整数，其取值范围为

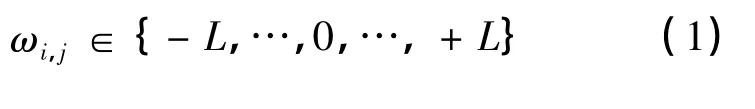
其中:L代表神经网络中突触的深度;i=1，…，K表示第i个隐藏单元;j=1，…，N代表每个隐藏单元的第j个输入神经元。输入值为二进制:

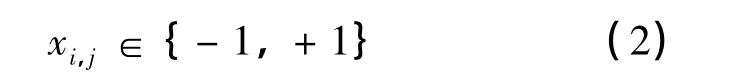
第i个隐藏单元输出值被定义为

TCM的总输出τ由其所有隐藏单元输出值相加得到:

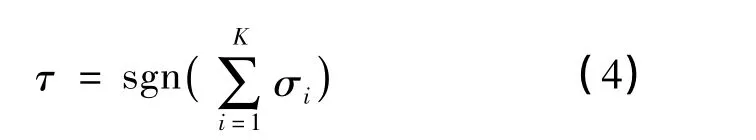
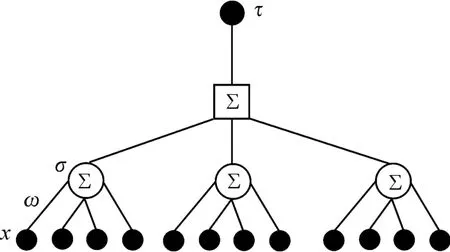
图1 TCM结构(K=3，N=4)

1.2 算法思想

通信双方A和B要求拥有同样的网络结构。在同步过程的开始阶段，两个神经网络随机地初始化它们各自的离散权值，表示为ωA/B，每次同步时A与B都使用相同的输入向量。

A与B根据式(3)算得各自的σA，σB，再根据式(4)算出τA和τB。A和B将各自的输出值进行交换，如果输出值相同，它们就开始相互学习，其各自的权值会通过一种特定的学习规则来进行更新。常用的学习规则有3种，分别是Hebbian学习规则、Hebbian反规则和随机游走规则［7］。如果输出值不相同则重复上述步骤。

经过多次相互学习后，A与B能完全达到同步，这意味着WA=WB，这个相同的权值就是 A和B共同参与下协商的会话密钥。

在密钥协商过程中，权值有两种更新方式:

1) 积极步骤(τA=τB=)。A与B对应的第i个隐藏单元下的权值会朝一个方向更新，积极步骤会促进同步的进程。积极步骤的发生概率为Pa。

2) 消极步骤(τA= τB，)。A与B对应的第i个隐藏单元中只有1个隐藏单元下的权值会更新，消极步骤会阻碍同步的进程，发生的概率为Pr。

积极步骤的发生概率和消极步骤的发生概率统称为转移概率。

2 TCM和TPM算法安全性比较

2.1 同步程度参数

在进行算法安全性讨论之前，需要引入一个重要的同步程度参数——权值重叠度ρ。它表示通信参与者A和B两个神经网络中权值的相似程度。为了方便表示，以下所有计算都基于1对对应隐藏单元。

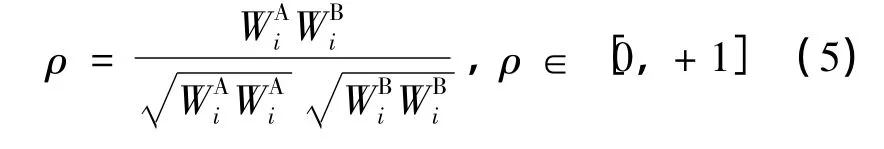
在同步开始时，随机的初始权值ρ=0。通过一系列的相互学习后达到同步，ρ=+1。在学习过程中，对应的两个隐藏单元不等的概率定义为ε。

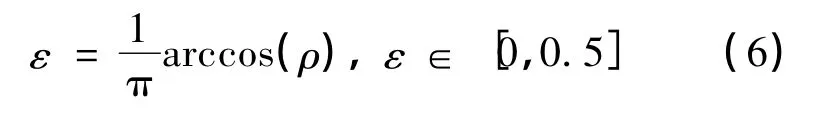
为了研究同步过程中ρ的动态原理，需要了解在每个学习步骤中重叠度ρ的平均变化:

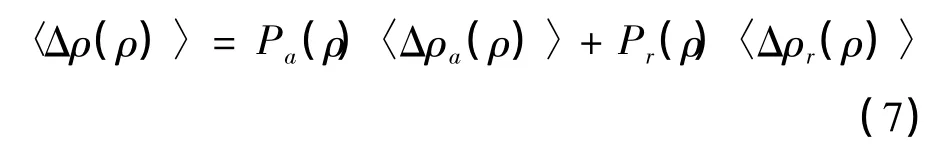
其中:〈Δρa(ρ)〉(〈Δρr(ρ)〉)表示每次积极步骤(消极步骤)中ρ的平均变化量。

2.2 安全性条件

安全的神经密码协议要求随着网络突触深度L的增加，A和B相互学习(双向同步)的平均同步时间以多项式率增长，而单向学习E的平均同步时间以指数率增长。根据平均同步时间的映射关系:

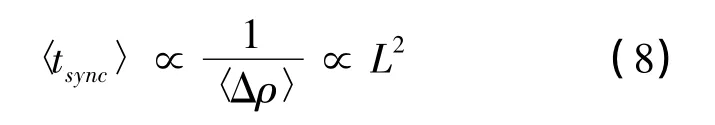
可知〈Δρ(ρ)〉＞0能使同步的时间随着L增加以一种多项式率增长。

由此得出神经密码的安全性条件:密钥协商算法中双向同步的重叠度平均改变量必须满足

将式(7)代入式(9)可得

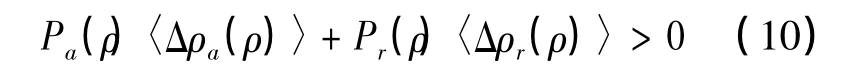
其中〈ρa(ρ)〉和〈ρr(ρ)〉都只依赖于运动方程［9］。根据运动方程，为方便后面的分析，将式(6)代入式(10)，改写为:

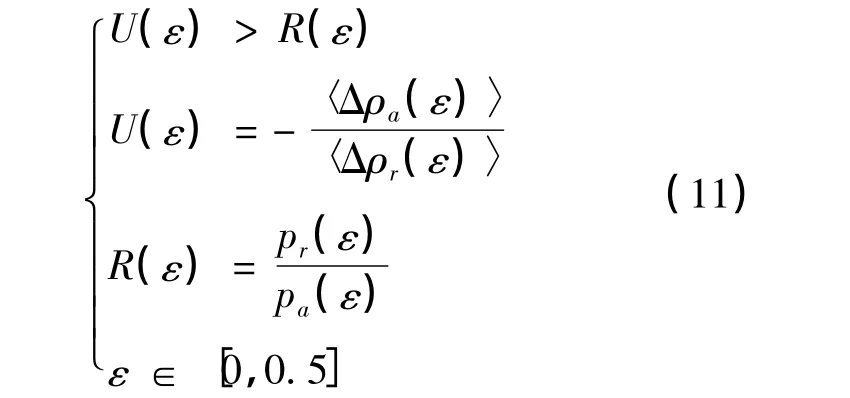
仅当M＜1时，算法满足安全性条件。

由于TPM(k=3)是一种安全的神经密码结构，而TCM(k=3)不是安全的神经密码结构［8］，本文以此为例来比较两种算法的差异。

下面分别计算TPM与TCM的转移概率。

由于TPM与TCM的运动方程相同，当ρ→1，ε→0时，由式(14)可以得到:

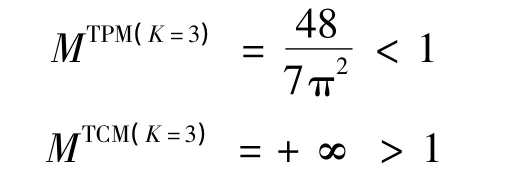
显然，TPM满足安全性条件，TCM不满足安全性条件。

图2是TPM与TCM算法中双向同步平均重叠度改变量与重叠度的关系。仿真结果验证了上述理论的正确性。

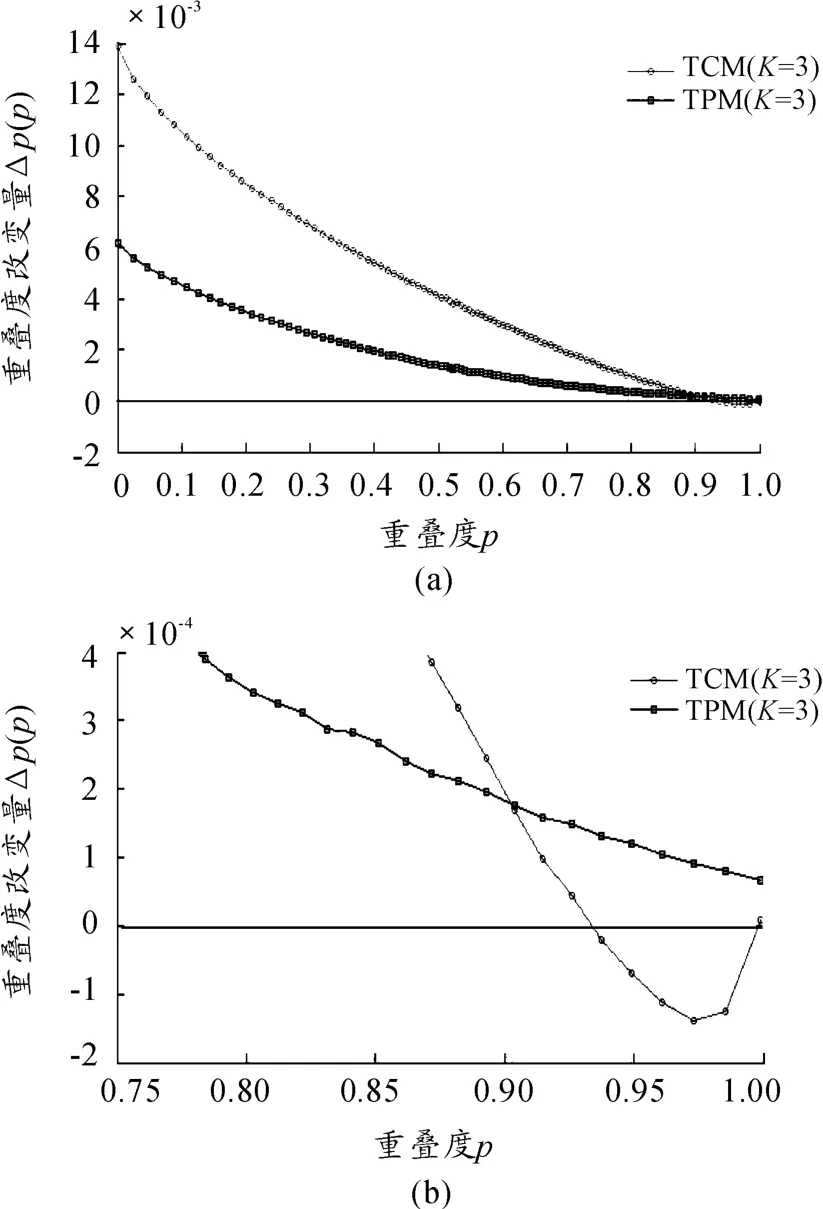
图2 〈Δρ(ρ)〉与 ρ的关系(K=3，L=10，N=1 000)

TPM和TCM的运动方程相同，其安全性的差异主要取决于R(ε)。R(ε)则由同步过程中消极步骤概率和积极步骤概率来决定。

由上文可知，积极步骤和消极步骤发生的概率与两个神经元中对应隐藏单元的情况有关。这里将两个神经网络中对应的隐藏单元称为一对隐藏单元。在TPM与TCM中，两个神经元对应的隐藏单元都相等，则它们的权值会发生积极步骤。在权值接近同步时，两种算法中积极步骤发生的概率都会趋向一个与K有关的实数，即(ε)～，(ε)～。但在TCM中，神经元中一对或多对隐藏单元不相同，权值都会发生消极步骤的更新，而TPM中当且仅当有两对不同时才发生消极步骤。因此，在权值接近同步时，两种算法中消极步骤发生的概率不同(ε)～2ε2，(ε)～可以看出，TCM机制中消极作用的发生概率要大于TPM，这是导致它们R(ε)不同的关键。因此，为了提高TCM机制的安全性，必须降低其中消极步骤作用发生的概率，减少权值发生消极步骤更新的情况，以满足安全密码协议的要求。

3 一种基于分类的TCM改进算法

基于上述问题，本文提出一种基于TCM的改进模型TCCM，并基于改进模型设计了新型的密码协议。该协议的优点是可通过分类因子H将TCM机制中的隐藏单元重新分类来减少同步学习中消极作用发生的情况，从而降低消极作用的概率，进而提高TCM的安全性。

3.1 TCCM 模型架构

TCCM结构见图3。TCCM在TCM基础上增加了一个分类因子H，其他的参数均不变。其中:

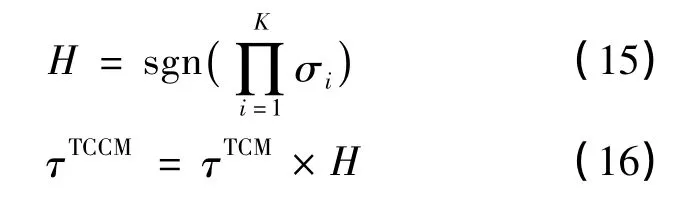
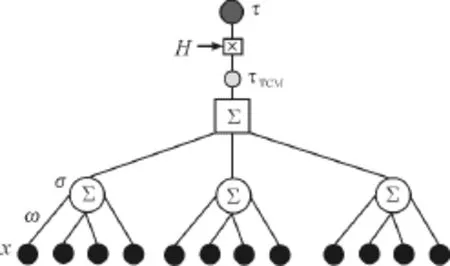
图3 TCCM结构(K=3，N=4)

3.2 TCCM算法描述

TCCM算法与TCM算法的不同点在于:在每次同步过程中，A与B分别计算出各自的输出值和，然后在公共信道上交换它们的输出值，同时σA/B要求保密。

改进后的Hebbian学习规则:

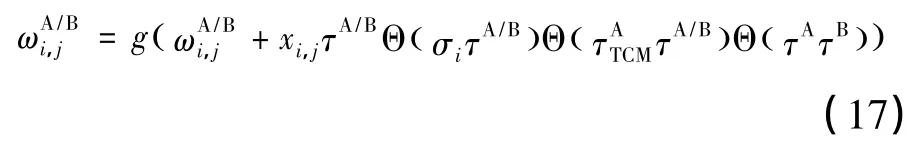
改进后的Hebbian反学习规则:

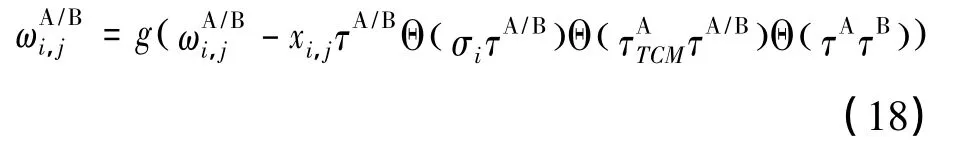
改进后的随机游走学习规则:

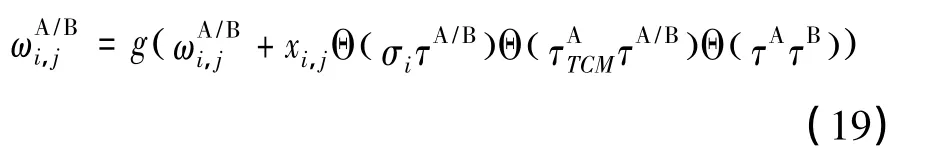
重复上述步骤直至权值达到同步，最后的权值可以作为A和B的公共密钥。

下面分别讨论TCCM(K=3)和TCCM(K=5)的隐藏单元分类情况。

从表1～2可以看到:在TCCM算法双向同步中，两个神经网络中对应的隐藏单元当且仅当有两对不相同时才发生消极作用。和TCM算法相比，TCCM算法降低了消极作用发生的概率。

3.3 TCCM算法的可行性

下面通过计算TCCM的转移概率并根据本文的算法安全性条件，从理论的角度来验证新算法的可行性。

TCCM的转移概率计算如下:

由以上可知，TCCM(K=3)和TCCM(K=5)都满足算法安全性条件。

表1 TCCM(K=3)的隐藏单元分类

表2 TCCM(K=5)的隐藏单元分类表

4 实验结果

TCM(K=3)与TCM(K=5)平均步长改变量与权值重叠度的关系如图4所示。其中 N=1 000，L=10。图4 表明:TCM(K=3)与TCM(K=5)在同步过程中，平均重叠度改变量始终大于0，满足安全性条件。

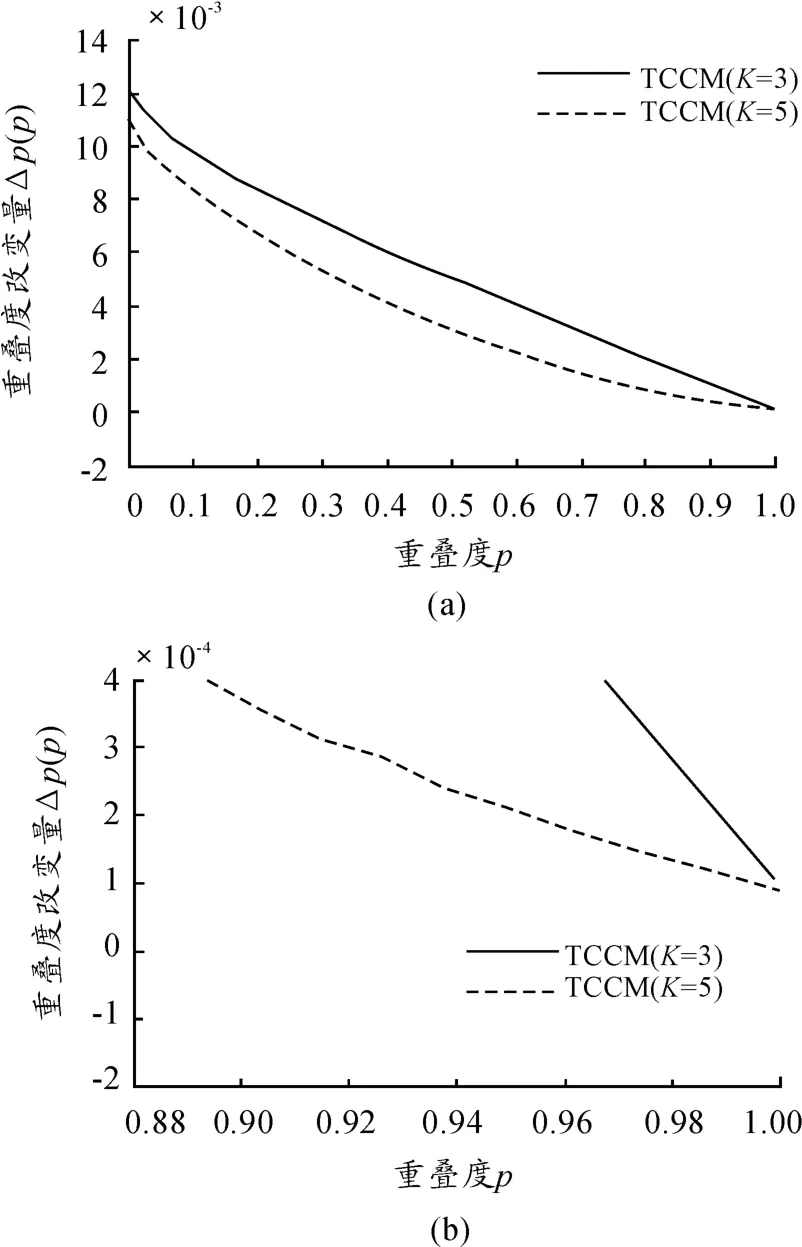
图4 TCCM 中〈Δρ(ρ)〉与 ρ的关系

大多数攻击和遗传攻击是以简单攻击和几何攻击为基础的高级攻击。通过观察算法抵御简单攻击和几何攻击的能力，大致可推断出其抵御高级攻击的效果。本文定义成功率为:在同步时间中，攻击者能获取被攻击者98%的权值的概率。图5～6为TPM、TCM和TCCM算法抵御简单攻击的性能对比，其中N=1 000，采用随机游走学习，进行10 000次试验后取平均值。图5～6表明:随着突触深度L的增加，3种算法的抗简单攻击能力都有所增强。在相同L条件下，TCCM的抗攻击性要比TCM强，与TPM相似。

图7～8为TPM、TCM和TCCM算法抵御简单攻击的性能对比。其中N=1 000，采用随机游走学习，进行10 000次试验取平均值。图7～8表明:随着突触深度L的增加，3种算法的抗几何能力都有所增强。在相同的隐藏单元个数下，抗几何攻击相比抗简单攻击的成功率更高。由于TCCM有两个输出值，在几何攻击中加大了对攻击者的干扰，因此，TCCM算法在相同的L值下相比其他两种算法具有更高的抗攻击性。

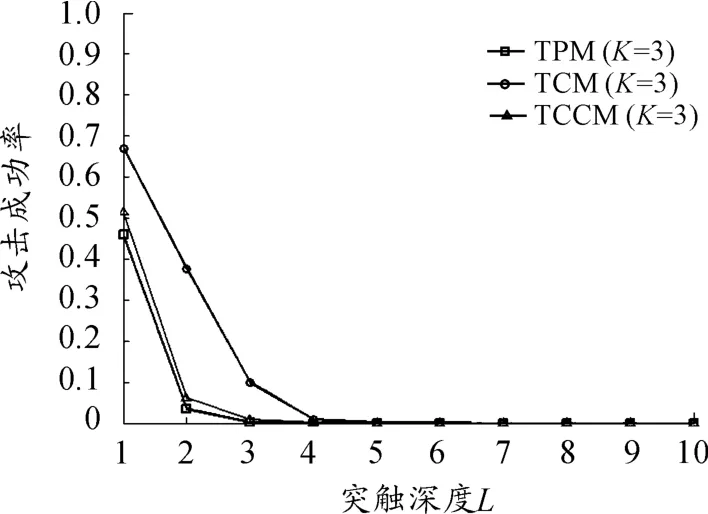
图5 简单攻击中3种算法(K=3)的性能比较

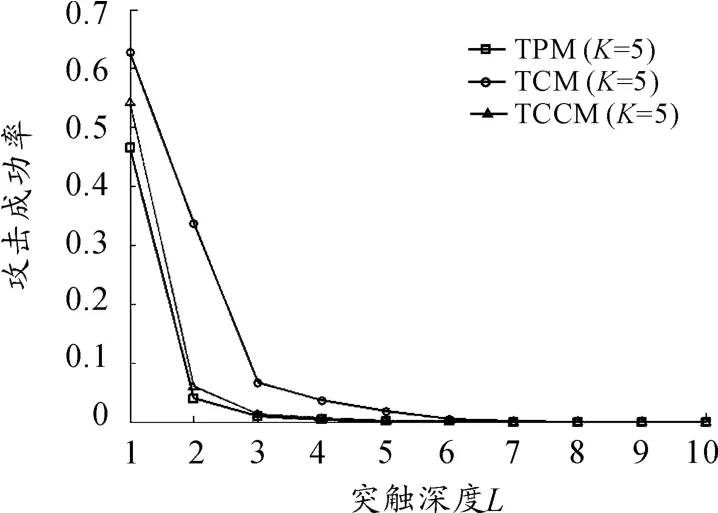
图6 3种算法(K=5)抵御简单攻击的性能比较

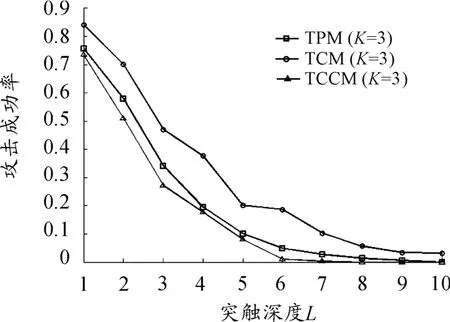
图7 3种算法(K=3)对于几何攻击的性能比较

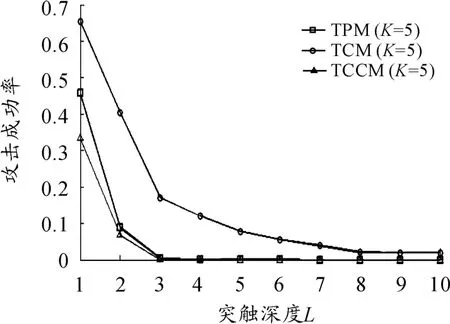
图8 3种算法(K=5)对于几何攻击性能比较

实验结果表明:TCCM算法在选择适当参数的情况下与TPM、TCM相比，其安全性能更高，能够有效抵御各种高级攻击。

5 结束语

本文研究了基于TCM的神经网络同步的密钥协商算法，通过与安全性较高的TPM算法进行比较研究，提出了一种更安全的分类式TCM-TCCM算法，为神经密码提供了一种新的安全网络模型。下一步研究的重点是解决如何将神经密码算法运用于传感器网络、RFID网络的安全通信中。

［1］Allam A M，Abbas H M.Group key exchange using neural cryptography with binary trees［C］//Canadian Conference on Electrical＆ Computer Engineering.IEEE.［S.l.］:［s.n.］，2011:000783 －000786..

［2］Diffie W，Hellman M E.New directions in cryptography［J］.Information Theory，IEEE Transactions on，1976，22(6):644－654.

［3］Jhajharia S，Mishra S，Bali S.Public key cryptography using neural networks and genetic algorithms［C］//International Conference on Contemporary Computing.［S.l］:IEEE，2013:137 －142.

［4］On-line learning in neural networks［M］.Britain:Cambridge University Press，2009.

［5］Allam A M，Abbas H M，El-Kharashi M W.Security analysis of neural cryptography implementation［C］//IEEE Pacific Rim Conference on Communications，Computers ＆Signal Processing.［S.L.］:IEEE，2013:195 －199.

［6］Allam A M，Abbas H M，El-Kharashi M W.Authenticated key exchange protocol using neural cryptography with secret boundaries［C］//International Joint Conference on Neural Networks.［S.L.］:IEEE，2013:1 －8.

［7］Li-sheng Z，Wei Y，Cheng-e L.New learning rule of neural cryptography based on queue mechanism［Z］.Application Research of Computers，2014.

［8］N M，X L，T H.Approach to design neural cryptography:a generalized architecture and a heuristic rule［J］.Phys Rev E Stat Nonlin Soft Matter Phys，2013，87(6):102 －10.

［9］Lei X，Liao X，Chen F，et al.Two-layer tree-connected feed-forward neural network model for neural cryptography［J］.Physical Review E Statistical Physics Plasmas Fluids＆ Related Interdisciplinary Topics，2013，87(3):1079－1094.

［10］Ruttor A，Kinzel W，Naeh R，et al.Genetic attack on neural cryptography［J］.Physical Review E，2006，73(3):036121.

［11］Shacham L N，Klein E，Mislovaty R，et al.Cooperating attackers in neural cryptography［J］.Physical Review E，2004，69(6):066137.