ArcGIS空间校正对比实验分析

伍 艳，白 林

(成都理工大学 数学地质四川省重点实验室，四川 成都 610059)

0 引 言

ArcGIS 是目前世界具有代表性的地理信息系统，其空间校正工具被广泛用于原始数据的粗加工、图形的修正、坐标的简单转换等.通常采用SHAPE文件格式将地理空间资料以坐标点串的形式存储起来，几乎所有的GIS 软件都支持对它的转换甚至支持对其直接进行读写操作，是现今GIS 界的一种标准格式，因此对通用的数据格式的校正是十分必要的［1］.

ArcGIS 是目前广泛用于地质数据处理的信息系统，其空间校正多用于地图数字化，不同纸质地图和影像地图的数字化多采用空间校正.空间校正中的射影校正多用于图像配准［2］，ArcGIS 中的空间校正模块是多维数学模型，可对地质图、纸质图、影像图进行配准，本研究选用的是二维空间校正模型，从空间校正的通用数学理论来比较3 种常用空间校正的特征.

1 空间校正算法模型对比分析

计算机科学研究的图像是真实世界(即二维或三维欧氏空间)到像平面的射影变换.如何提取真实世界的信息十分重要.若要在像平面中确定l∞的像，可以将射影变换变成仿射变换，消除射影变换的变形;一旦确认虚圆点，仿射变换就可以恢复到相似变换，消除仿射变形.对于余下相似变形，需要用真实世界的测量和度量单位消除.3 种变换关系如图1所示.

图1 空间校正关系图

E1:射影变换到仿射变换

在射影变换下，无穷远点可以映射为有限点，因此l∞可以被映射为有限直线.在仿射变换下，l∞不会被映射为有限直线，仍留在无穷远处，即仿射变换保持直线的平行性，推出如下模型［3］，

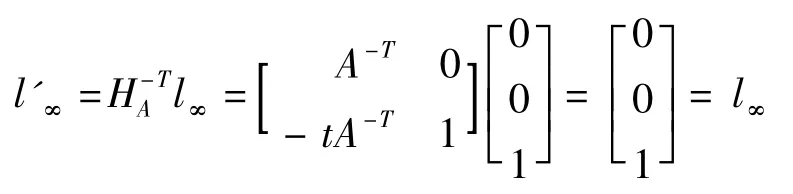
即仿射变换是保持l∞不变的射影变换，H 是射影变换，A 是射影变换矩阵.

E2:射影变换到相似变换［4］

在相似变换下，l∞上有2 个不动点，为虚圆点(也称绝对点)，记为I，J，其标准坐标表示为，

这一对虚圆点是复共轭理想点，在保持相似变换方向不变的情况下，模型如下，

即在射影变换H 下，虚圆点I 和J 为不动点当且仅当H 为相似变换.

E3:仿射变换到相似变换

仿射变换又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间.常用二维数学模型为，

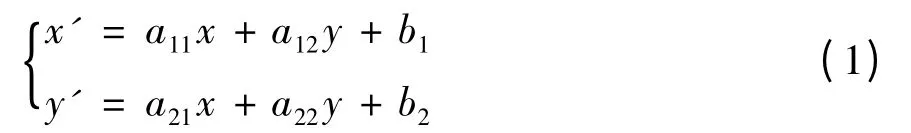
式中，a11、a12、a21、a22为4 个基本比例参数，b1、b2为2 个平移配准参数，x、y 为原变量，x'、y'是目标值.通常采用的6 参数模型利用模型计算配准参数，用最小二乘法达到用多个配准点拟合出最优参数解得目标值.

仿射变换可以简化为相似变换，即经过坐标系的平移、旋转和比例变换实现，其数学模型为，

相似变换至少需要2 个定向点，才能求解出4个参数.为了减少误差影响，探测粗差，应选择m ≥2 个已知点，就会产生不符值.可按最小二乘法求解上式中的系数.

对于仿射变换到相似变换，参数得到简化，模型变得更简单.

综上所述，射影变换、仿射变换、相似变换满足一定条件下可以相互转换，并且射影变换是三者中最为复杂、相对运用最广的模型.射影校正可以是多维的数学模型，其二维数学模型为，

式中，a1、b1、d、e 和a2、b2、d、e 为2 组4 个基本比例参数，c、f 为2 个平移配准参数，x、y 为原变量，x'、y' 是目标值.射影校正至少需要4 个位移关联才可求得参数.

射影变换可以分解为仿射变换、相似变换、射影变换的组合［5－6］，其方式为，

式中，A = sRK + tvT/v 是非奇异矩阵，K 是满足detK= 1 的归一化上三角矩阵.当v ≠0，分解成立，取s为正，分解唯一.

矩阵HS、HA、HP分别是相似变换、仿射变换和射影变换.HP移动无穷远直线，HA改变仿射性质，但保持无穷远直线在无穷远处.HS是一般相似变换，它不改变仿射及射影性质，变换HP属于透视变换.对射影变换，有2 个约束，就可以消除射影变形，有4个约束消除仿射变形.在二维平面空间校正中，射影变换在4 个约束下，是3 种变换中最佳选择.

2 实验分析

本研究选取的实验数据为道路(road)和设计(design)2 个图层，将设计图层通过空间校正方法校正到道路中去.建立空间校正的链接文件，提取需要校正的图层的校正点坐标位置及目标图层的校正点坐标位置，形成.txt文本文档，如图2 所示.

图2 原始实验数据

通过运用3 种空间校正的方法依次对原始数据图层进行校正，选择拐点等标志性位置得出校正结果如图3 所示.通过直接比较，无法看出图形之间的误差，通过对校正结果进行误差分析，得出表1 和表2 的实验结果.

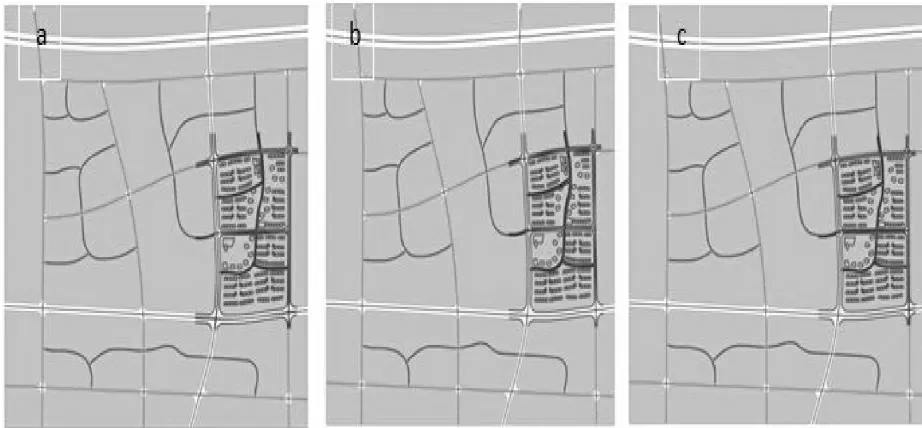
图3 3 种空间变换校正结果

根据空间校正3 种数学模型，选取4 个位移连接，用最小二乘法进行参数求解，求得空间校正3 种模型的误差精度［7］.

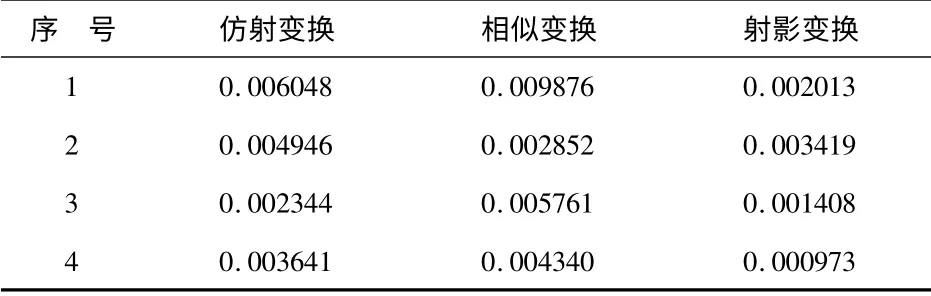
表1 参数误差精度

坐标校正参数求解后，在目标图层上选择3 个要素点(x'a，y'a)、(x'b，y'b)和(x'c，y'c)分别带入式(1)、(2)、(3)，可得仿射变换、相似变换、射影变换的坐标值，即(xa，ya)、(xb，yb)和(xc，yc).这样需要校正的原始图层校正点就有4 种坐标值，即(x，y)、(xa，ya)、(xb，yb)和(xc，yc).以(x，y)为真值，可以得到仿射变换、相似变换、射影变换的真误差，分别用△xa、△ya、△xb、△yb和△xc、△yc表示，即△xi= xi－ x(i = a，b，c)，点位误差为，

得出每次校正中的误差计算式如式(5)，n 为点的个数，结果见表2.

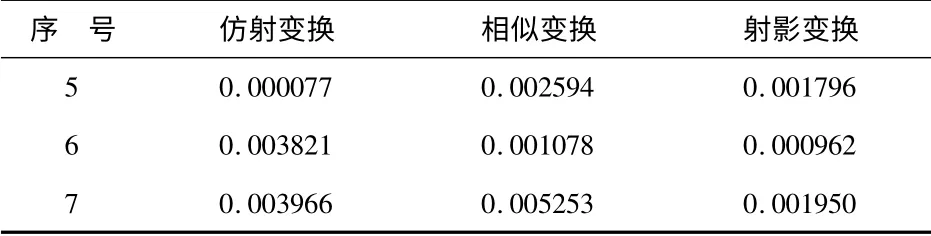
表2 校正精度误差

通过表1 和表2 的2 组数据，绘制空间校正的误差分布图，如图4 所示.

图4 空间校正误差分布图

由图4 可知，射影变换的误差走势趋于平缓，而仿射变换的误差变化最大，由于选取的是二维笛卡尔坐标系，对于相似变换优于仿射变换，选取的校正点多为拐角、折线交点，因此，射影变换优于仿射变换和相似变换［8］.

相对于仿射变换，相似变换不会对于轴单独缩放，对于一般地图矢量数据，采用笛卡尔直角坐标系，因此，对于通用坐标系下，横纵轴的坐标不会改变，相似变换虽然是仿射变换的特例，却是在保持要素的相对形状下，优先选择相似变换.

对于选取的design 图层到roadcenter 的校正，属于二维矢量数据的校正.选取的点都是折线交点，因此，对于保持变换前后的不连续性，射影变换的RMS 误差是最小的.

3 结 论

地质工作中数据的后期处理非常重要，尤其数据不全纸质档案及图片影像等，对于空间校正的准确度要求非常高.对此，本研究比较了3 种常用的校正方法，希望能够对数据的校正提供更精确的指导，为后续工作减少误差.

本研究讨论了仿射变换、相似变换、射影变换.从广义的角度来说，3 种变换方法都是线性变换，只是参数、精度及适用范围不同.对于仿射变换，保留原始图层的平行线、平行线段的长度比、面积比不变.相似变换适用于常用的直角坐标系中变换，保持要素的相对形状条件下，避免图层的扭曲.由于二维矢量数据的校正，选取的点都是折线交点，对于保持图层变换前后的不连续性，射影变换具有优势.

［1］牟乃夏，刘文宝，王海银，等.ArcGIS10 地理信息信息系统教程［M］.北京:测绘出版社，2012.

［2］樊敏，秦健，李云响，等.ArcGIS 数字化地质图校正及配准［J］.化工矿产地质，2014，36(3):185－189.

［3］于光辉，卢洪义，朱敏，等.基于相似变换的CT 图像缺陷定位方法［J］.CT 理论与应用研究，2012，21(1):37－42.

［4］房新玉，闻道秋，张秀梅，等.相似变换在大比例尺地形图的投影换带中的应用［J］.现代测绘，2006，29(6):36－38.

［5］郭金运，朱明法，徐泮林.地图数据几何纠正时仿射变换与相似变换的对比分析［J］.测绘通报，2001，47(4):23－24.

［6］胡茂林.空间变换［M］.北京:科学出版社，2007.

［7］【德】赫普克.误差理论与平差计算［M］.田佩俊，译.北京:煤炭工业出版社，1989.

［8］罗聚胜，杨晓明.地形测量学［M］.北京:测绘出版社，2001.