一阶逻辑公式相对真度的计算形式

秦晓燕，徐 扬

1.山西师范大学数学与计算机科学学院，山西临汾041004

2.西南交通大学智能控制开发中心，成都610031

一阶逻辑公式相对真度的计算形式

秦晓燕1，2，徐 扬2

1.山西师范大学数学与计算机科学学院，山西临汾041004

2.西南交通大学智能控制开发中心，成都610031

对二值谓词逻辑中一阶公式关于有限解释的相对真度定义进行了简化，给出其计算形式。指出一阶非闭逻辑公式的相对真度只与其中自由出现的变元有关，而非只与其中的自由变元有关；证明可以增加公式中出现的变元个数，而不会改变公式的相对真度，从而可以依据相对真度的计算形式横向研究公式间的相对真度问题。

相对真度；有限解释；自由出现变元；计量谓词逻辑

1 引言

人工智能是研究如何使计算机模拟人的思维过程和智能行为的学科，其中普遍采用的是精确的、形式化的逻辑推理方法。但是，本质上来讲，人脑的思维模式和推理方法是带有不确定性的近似推理，而不是精确化的推理。因此，近年来程度化的推理越来越受到人们的关注。关于计量逻辑的研究是其中一个重要的研究方向。计量逻辑[2]的内容分五部分：逻辑公式的真度理论、逻辑公式间的相似度理论、逻辑度量空间、近似推理理论以及理论的相容度理论，其中逻辑公式的真度理论是整个计量逻辑理论的奠基石。另一方面，计量逻辑由计量命题逻辑与计量谓词逻辑组成，其中计量命题逻辑已得到深入而系统的大量研究成果（比如，文[2-12]），但计量谓词逻辑却只有零星成果[13-17]。

实际上，由于一阶逻辑中解释的复杂性，现有的关于计量谓词逻辑的研究成果也都是在解释域有限的局限下得到的[13-17]。除文献[13]以语构角度提出一阶公式的公理化真度外，文献[14-17]均以语义角度出发，基于公式在有限解释下的相对真度出发展开研究，并且相对真度的定义都是以测度形式给出的。本文首先给出有限解释下一阶公式相对真度的计算定义形式，简化了其计算过程与证明过程。接着，证明了赋值是否满足公式完全取决于其在公式中自由出现的变元上的赋值，而非文献[1]中所指出的“由赋值在自由变元上的赋值决定”。最后，证明了可以适当增加公式中出现的变元个数而不改变其相对真度，从而更好地证明关于相对真度的一些性质，为进一步研究一阶公式的各种真度理论提供更为坚实的理论基础。

2 预备知识

设L是不含函数符号的一阶语言（这是合理的，在文献[18]中证明了这种语言的一般性），M=(M，(rP)P，(mc)c)是L的一个解释，其中M是一个非空集合，称为解释M的论域，rP是与谓词符号P对应的上M的关系，mc是与个体常元c对应的M中的元。L在M中的赋值v：T→M是从L的项集T到M的一个映射，且满足v(c)=mc，v(x)∈M，其中c为个体常元，x为变元，且∀t∈T，t为个体常元或变元。在公式(∀xi)A中，A叫做∀xi的辖域。这时公式A中若有变元xi，则该xi叫约束变元。又，∀xi中的xi也叫约束变元。不是约束变元的变元叫自由变元。

在本文中，记全体谓词公式之集为F，全体L在M中的赋值之集为ΩM。又，记全体变元集为S，记全体论域为非空有限集的解释之类为Mf，且∀v∈ΩM，若v满足公式A，记为‖‖AM，v=1，否则记为‖‖AM，v=0。记非空有限论域M的势为|M|。

其中m=1，2，…。μ被称为{μn}∞n=1的无限积，概率测度空间(X，A，μ)称为概率测度空间{(Xn，An，μn)}∞n=1的笛卡尔乘积，简记为X。

设M=(M，(rP)P，(mc)c)∈Mf，令Xn=M，μn是Xn上的均匀分布概率测度，即μ(X)=1，μ(∅)=0，μ(F)=nnnn这里F⊆Xn(n=1，2，…)。又因为M有限，所以任一Mm的子集都可测(m=1，2，…)。由定理2.1，在XM==M∞上存在{的无限积测度μM，并且对任一Mm的子集E，其测度μM(E)均可通过式（1）来计算(m=1，2，…)。另外，由于个体常元在解释M下的值固定，即对任意一阶语言L在解释M中的赋值v，v(c)=mc固定不变，故L在M中的赋值v完全v由在变元集S={x1，x2，…}上的限制v|S而定。因此设v∈ΩM，v(xk)=vk(k=1，2，…)，则有唯一的v=(v1，v2，…，vn，…)∈XM与之对应；反过来，若v=(v1，v2，…，vn，…)∈XM，则存在唯一的v∈ΩM，使得v(xk)=vk(k=1，2，…)。因此在ΩM与XM之间存在一一对应φ，其中φ(v)=v。

定义2.2[14]设M∈Mf，A∈F。定义[A]M与τM(A)如下：

[A]M={v∈XM|v∈ΩM，‖A‖M，v=1}

则称τM(A)为公式A关于解释M的相对真度。

命题2.3[14]设M∈Mf，A，B∈F。则

（i）0≤τM() A≤1；

（ii）τM(¬A)=1-τM(A)；

（iii）若A～B，则τM(A)=τM(B)。

3 相对真度的计算定义形式

在定义2.2中，一阶公式关于有限解释的相对真度是以测度形式给出的，而且其中的测度是均匀概率测度，即对任意集合F⊆XM，则μM(F)=。所以，可以直接给出它的数值计算形式，这样，会使一阶公式关于有限解释的相对真度的实际计算与相关命题证明更加简捷明了。事实上，对于某一个具体的一阶公式A，其中出现的变元是有限的，假设为x1，x2，…，xk(k=1，2，…)，那么在某个已知有限解释M下，对任意赋值v∈ΩM，v是否满足公式A完全由v对A上出现的所有变元的赋值决定。所以，式（2）中的[A]M可以更具体的定义为：[A]M={(v(x1),v(x2),…,v(xk))∈Mk|,v∈ΩM,‖‖AM，v=1}（3）

因此，若公式A中所有出现的变元为x1，x2，…，xk，则按照定义2.2，

也就是如下的公式关于有限解释的数值计算形式：

定义3.1设M∈Mf，A∈F，且A中出现的变元共有k个。定义τM(A)如下：

其中[A]M定义为式（3），则称τM(A)为公式A关于解释M的相对真度。

注3.1由式（4），公式A关于有限解释M的相对真度只与其中出现的谓词符号与个体常元的解释，以及A中出现的变元有关。但是，值得注意的是，它与变元的符号并没有关系。也就是说，若x在公式A中出现，则将x换为不在A中出现的y后，公式A关于解释M的相对真度不变。当然，这种变换只是保持其真度不变，而并不能使得变换前后的公式逻辑等价。

例3.1设L是一阶语言，它有一个个体常元c，一个一元谓词符号Q。M=(M，{rQ}，{mc})是一阶语言L的一个解释，其中M是一个非空有限集。现有B=Q(x)→(∀x) Q(x)∈F，计算τM(B)。

解：公式B中只有一个变元x。

注意到，在解释M下，对任意赋值v∈ΩM，‖(∀x)Q(x)‖M，v=1当且仅当rQ=M。因此，有：

若rQ=M，则对任意赋值v∈ΩM，‖Q(x)‖M，v=1，且‖(∀x)Q(x)‖M，v=1，从而，[B]M=M-∅=M；

若rQ≠M，则对任意赋值v∈ΩM，均有‖(∀x)Q(x)‖M，v=0，从而，[B]M=M-rQ。

由式（4），公式B关于解释M的相对真度τM(B)为：

容易证明

命题3.1设M∈Mf，A，B∈F。A与B中出现的变元相同，且个数为k(k=1，2，…)。

（i）A是关于解释M的真公式当且仅当[A]M=Mk；A是关于解释M的假公式当且仅当[A]M=∅；

（ii）若A是闭公式，则要么[A]M=Mk，要么[A]M=∅；

（iii）若A与B逻辑等价，则[A]M=[B]M；

（iv）[¬A]M=Mk-[A]M，[A∧B]M=[A]M∩[B]M，[A∨B]M=[A]M∪[B]M。

前面说到，对某个具体的一阶公式A而言，在某个有限解释M下，赋值v∈ΩM是否满足公式A完全由v对A中出现的变元的赋值决定。实际上，可以更精确地说，v是否满足公式A完全由v对A上自由出现的变元的赋值决定。在文献[1]中有命题3.2.25：

“设L是一阶语言，M是L的一个解释，A∈F，v与w是L在M中的两个赋值。如果对A中的每个自由变元xi都有v(xi)=w(xi)，则v满足A当且仅当w满足A。”

但是，这个命题是错误的。可以举出一个反例来说明。设A=P(x，y)→(∀x)Q(x)，解释M下：论域M={0，1，2}，rP={(a，b)|a＜b}，rQ={a|a＞0}。显然公式A中只有一个自由变元y，而变元x不是自由变元，但在A中自由出现1次。取解释M下的两个赋值v与w，使得v(y)= w(y)=1，并且v(x)=2，w(x)=0，则显然有‖P(x，y)‖M，v=0，且‖P(x，y)‖M，w=1，而‖(∀x)Q(x)‖M，v=‖(∀x)Q(x)‖M，w=0。所以‖‖AM，v=1，但是‖‖AM，v=0。即：虽然v与w在A中每个自由变元的值都相等，但v与w并不同时满足A。

记A=B→C，B，C中的自由变元之集分别为FA，FB，FC，则显然应该有FA⊆FB∪FC。文献[1]中命题3.2.25的证明错误之处就在于，误认为FA=FB∪FC。比如，A=P(x，y)→(∀x)Q(x)，其中B=P(x，y)，C=(∀x)Q(x)，显然，FA={y}，FB={x，y}，FC=∅。所以FA⊆FB∪FC，而不是FA=FB∪FC。

具体来说，在文献[1]命题3.2.25的证明中有：“（ii）设A是B→C且已证明v满足B当且仅当w满足B，v满足C当且仅当w满足C，则仍易推出v满足A当且仅当w满足A。”这一步是不能成立的。由于只是归纳总结了：“若对公式B中的自由变元，总有v=w()，则v满足B当且仅当w满足B；若公式C中的自由变元，总有v()=w()，则v满足C当且仅当w满足C。”由于{}⊆{}∪{}，所以虽然对所有，v()=w()，但并不能保证v与w一定同时满足v()=w()与v()=w()，也就不能得出“已证v满足B当且仅当w满足B，v满足C当且仅当w满足C”的结论了。因此也就不能继续下面的归纳推理了。

实际上，只要将命题3.2.25中的“自由变元”都改为“自由出现的变元”，那么命题的证明过程就不会中断了。因为若分别记A，B，C中自由出现的变元之集为GA，GB，GC，则显然有GA=GB∪GC。那么若对所有∈GA，总有v()=w()，就可以推出对所有∈GB与∈GC，总有v()=w()与v()=w()。从而“已证v满足B当且仅当w满足B，v满足C当且仅当w满足C”。因此，正确的结论应该是：

命题3.2设L是一阶语言，M是L的一个解释，A∈F，v与w是L在M中的两个赋值。如果对A中的每个自由出现的变元xi都有v(xi)=w(xi)，则v满足A当且仅当w满足A。

因此，若公式A不是闭公式，其中自由出现的变元为xi1，xi2，…，xir(r=1，2，…)，令

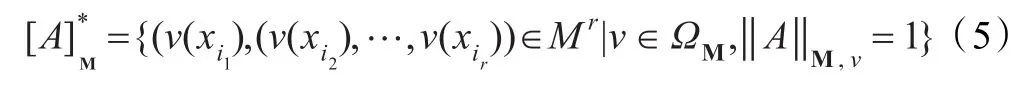
那么式（4）就变成：

例3.2设L是一阶语言，它有两个个体常元a1，a2，一个二元谓词符号P。设L的解释M为：

现有公式A为(∀x1)(P(x1，x2)→P(x2，x1))，计算τM(A)。

解：公式A中只有一个自由出现的变元x2，并且在解释M下，对任意赋值v∈ΩM，‖P(x1，x2)‖M，v=1-‖P(x2，x1)‖M，v。所以由式（5），

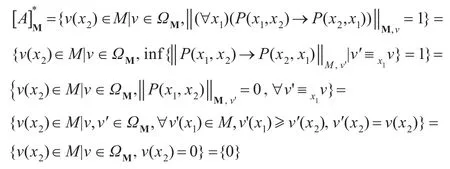
因此，由式（6）得，

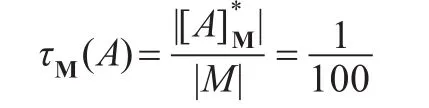
由定义3.1，可以看到公式关于有限解释的相对真度只与其中出现的变元有关。但是如果遇到研究两个或两个以上不同公式的真度的性质时，每个公式出现中的变元个数不同却成为运用相对真度计算形式的一个障碍。如果对每个公式变形，使得所有公式中出现的变元相同，但其相对真度不变，那么就可以利用相对真度的计算形式去研究相对真度的性质了。更进一步，如果对任一公式，都可以适当增加其中出现的变元，但不改变其相对真度，就可以实现所有公式出现的变元相同而各自相对真度不变的想法了。事实上，有如下定理：

定理3.1设M∈Mf，A∈F，且A中出现的变元为x1，x2，…，xk，则存在A′∈F，A′中出现的变元为x1，x2，…，xk，y1，y2，…，yl，且A′～A，从而τM(A')=τM(A)。

证明令A0=¬(P(y1，y2，…，yl)→P(y1，y2，…，yl))，A′=A∨A0，则显然A′～A，且A′中出现的变元为x1，x2，…，xk，y1，y2，…，yl。因为A′～A，由命题2.1（iii），τM(A′)=τM(A)。

注3.2通过定理3.1，可以将公式A变形为与之逻辑等价，相对真度不变，却出现更多变元的A′。更进一步，由于A′～A，所以在其他所有涉及公式A的逻辑公式（如A→B，¬A，(∀x)A等）的相对真度也不会改变。也就是说，在研究公式的相对真度的时候，可以不改变公式的相对真度而随意增加公式中出现的变元个数。因此，当研究两个或两个以上的公式的相对真度的时候，完全可以假设各自独立的公式出现的变元是相同的，从而横向研究公式间的相对真度的关系了。

由例3.1与例3.2看到，利用相对真度的计算定义形式来计算公式关于有限解释的相对真度时，其计算过程很简单。其实，计算定义形式不止在计算公式的相对真度时表现出其优越性，在证明某些关于相对真度的相关命题时，相较于其测度定义形式，更加直观简捷。

下面利用相对真度的计算形式来证明相对真度的一些简单性质，从中可以看到这种新的定义形式在证明关于相对真度的相关命题时的优越性。

命题3.3设M∈Mf，A，B∈F。

（ii）τM(A∨B)≥max{τM(A)，τM(B)}。

证明只需证明（i），（ii）同理可证。根据注3.2，假设A与B中出现的变元相同，均为x1，x2，…，xk，则A∧B中出现的变元亦为x1，x2，…，xk。由命题3.1（iv）与定义3.1，

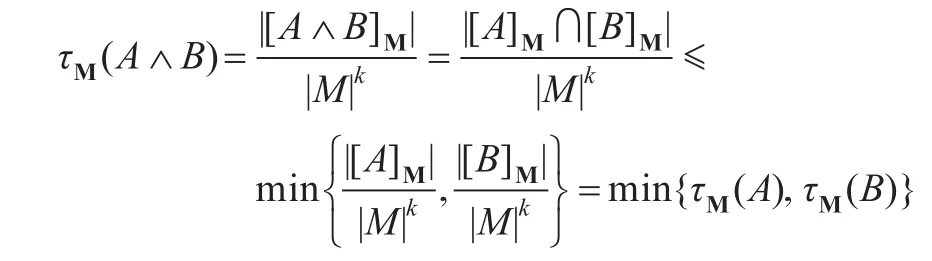
下面记F1为所有不含量词，且没有重复出现的谓词符号或变元符号的一阶公式之集。

定理3.2设A∧B∈F1，则对任一有限解释M=(M，(rP)P，(mc)c)∈Mf，总有τM(A∧B)=τM(A)τM(B)。

证明设公式A中所有出现的变元为x1，x2，…，xr，公式B中所有出现的变元为y1，y2，…，ys，其中r，s=1，2，…。那么根据定义3.1，

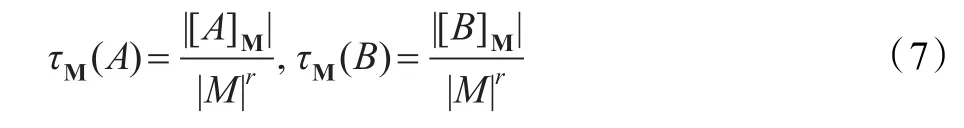
因为A∧B∈F1，所以A∧B中所有出现的变元为x1，x2，…，xr，y1，y2，…，ys，且它们互不相同。对任一解释M=(M，(rP)P，(mc)c)∈Mf，由于公式A与B中没有共同的谓词符号或变元符号，因此‖‖AM，v与‖‖BM，v的值互不影响。由式（3），

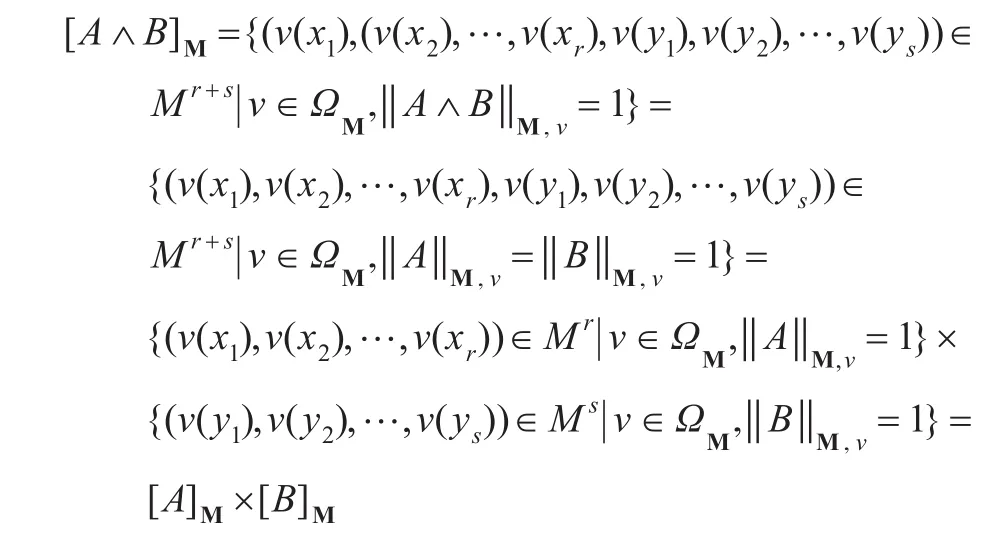
根据定义3.1与式（7），

推论3.1设A1∧A2∧…∧Am∈F1，若M=(M，(rP)P，(mc)c)∈Mf，则总有τM(A1∧A2∧…∧Am)=τM(A1)τM(A2)…τM(Am)。

定理3.3设A∨B∈F1，则对任一有限解释M= (M，(rP)P，(mc)c)∈Mf，总有τM(A∨B)=τM(A)+τM(B)-τM(A∧B)。

证明显然，如果A∨B∈F1，那么也一定有A∧B∈F1。因此，由命题2.1与定理3.1，对任一有限解释M=(M，(rP)P，(mc)c)∈Mf，

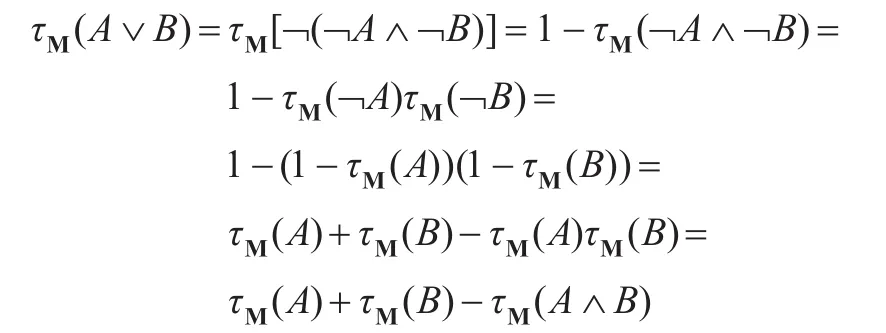
4 结束语

本文给出了一阶公式关于有限解释的相对真度的计算定义形式，举例说明这一新的定义形式在相对真度的计算和证明过程中较之测度定义形式更为直观简便；指出一阶公式的相对真度只与其中出现的变元有关，特别地，一阶非闭公式的相对真度只与其中自由出现的变元有关，而非文献[1]中指出的“与所有自由变元有关”；证明不改变公式的相对真度前提下，可以适当增加公式中自由出现的变元个数，以便横向研究公式间的真度问题。一阶公式相对真度作为计量谓词逻辑理论的奠基石，对它的计算定义形式的研究，是一件非常有意义的事情。

[1]王国俊.数理逻辑引论与归结原理[M].北京：科学出版社，2003：55-56.

[2]Wang G J，Zhou H J.Quantitative logic（I）[J].Information Sciences，2009，179：226-247.

[3]王国俊.非经典数理逻辑与近似推理[M].2版.北京：科学出版社，2008.

[4]王国俊，傅丽，宋建社.二值命题逻辑中命题的真度理论[J].中国科学：A辑，2001，31（11）：998-1008.

[5]Wang G J，Leung Yi.Integrated semantics and logic metric spaces[J].Fuzzy Sets and Systems，2003，136（1）：71-91.

[6]Hui X J，Wang G J.Randomized study on classical reasoning mode and its application[J].Science in China（Ser.E），2007，37（6）：801-812.

[7]韩邦合，李永明.计量逻辑学中的近似推理[J].模糊系统与数学，2010，24：1-7.

[8]周红军，王国俊.Borel型概率计量逻辑[J].中国科学：信息科学，2011，41（11）：1328-1342.

[9]Jun Li，Yan Zhou.A Quantitative method of n-valued Gödel propositional logic[J].Procedia Environmental Sciences，2012，12：583-589.

[10]折延宏，贺小丽.粗糙逻辑的计量化研究[J].计算机工程与应用，2012，48（14）：44-50.

[11]娄妍，冯飞，左卫兵.Lukasiewiczn值命题逻辑中公式的条件随机真度[J].计算机工程与应用，2012，48（33）：63-67.

[12]She Yanhong.On the rough consistency measures of logic theories and approximate reasoning in rough logic[J].International Journal of Approximate Reasoning，2014，55：486-499.

[13]王国俊.一类一阶逻辑公式中的公理化真度理论及其应用[J].中国科学：信息科学，2012，42（5）：648-662.

[14]王国俊，秦晓燕，周湘南.一类二值谓词逻辑中公式的准真度理论[J].陕西师范大学学报：自然科学版，2005，33（1）：1-6.

[15]Qin Xiaoyan，Liu Yi，Xu Yang.Theory of approximate reasoning in two-valued predicate logic based on the quasi-truth degrees[J].Journal of Donghua University，2012，29（1）：23-27.

[16]秦晓燕，徐扬，刘熠.二值谓词逻辑中公式的向量真度[J].模式识别与人工智能，2013，26（8）：740-744.

[17]Wang Guojun，Qin Xiaoyan，Zhou Xiangnan.An intrinsic fuzzy set on the universe of discourse of predicate formulas[J].Fuzzy Sets and Systems，2006，157：3145-3158.

[18]Hajek P.Metamathematics of fuzzy logic[M].London：Kluwer Academic Publishers，1998.

[19]Halmos P R.Measure theory[M].New York：Springer Verlag，1974.

QIN Xiaoyan1,XU Yang2

1.College of Mathematics and Computer Science,Shanxi Normal University,Linfen,Shanxi 041004,China
2.Intelligent Control Development Center,Southwest Jiaotong University,Chengdu 610031,China

The simplified computational definition of the relative satisfiability degrees of first-order formulae in a finite interpretation is proposed.It is pointed out that the relative satisfiability degree of a nonclosed first-order formula is just related to the free-occurred variables in the formula,not the free variables occurred in the formula；and it is proved that the relative satisfiability degree of a first-order formula can be unchanged although the amount of the variables occurring in the formula is increased,so that the matter of the relative satisfiablity degrees among formulae can be transversely studied according to the computational definition of the relative satisfiability degrees of first-order formulae.

relative satisfiablity degree；finite interpretation；free-occurred variables；quantitative predicate logic

A

O141

10.3778/j.issn.1002-8331.1504-0102

QIN Xiaoyan,XU Yang.Computing definition of relative satisfiability degrees of first-order formulae.Computer Engineering and Applications,2015,51（16）：6-10.

国家自然科学基金（No.61175055）；四川省科技支撑计划（No.2011FZ0051）；工业和信息化部无线电管理局（No.[2011]146）；中国通信学会（No.[2011]051）。

秦晓燕（1981—），女，博士研究生，讲师，研究领域为不确定性推理；徐扬（1956—），男，博士生导师，教授，研究领域为不确定性推理。E-mail：lisaqin1981@126.com

2015-04-12

2015-06-16

1002-8331（2015）16-0006-05