具有能量采集驱动的MIMO广播信道和多址接入信道最优传输方案

李文明

具有能量采集驱动的MIMO广播信道和多址接入信道最优传输方案

李文明

提出了一个新颖的方法来获得具有能量采集驱动的节点的最优传输方案，结合凸优化理论探索了多输入多输出（MIMO：multi-input multi-output）广播信道（BC：broadcasting channel）和MIMO多址接入信道（MAC：multi-access channel）网络结构中最优传输，设计了低复杂度的上下行对偶性嵌套优化算法、阻塞协作迭代提升算法获得信道传输中最大化的总吞吐量并研究所提出算法的实时、在线操作。其方案将对未来能量采集驱动的MIMO BC和MIMO MAC通信网络的设计和优化提供理论指导。

能量采集；广播信道；多址接入信道；功率分配；凸优化；迭代；高能效通信

0 引言

在新兴的能量采集网络中，带有可采集能量装置和可充电能量装置的无线设备可以从外界环境中采集可再生能源（如太阳能、风能等）进行通信。由于这些再生资源在本质上是间歇性的，导致收集到的能量中可供使用的能量额不均匀地改变，例如，总长为10秒的传输时段内，能量2、3、7、8焦分别在时刻0、2、5、9秒被采集，如图1所示：

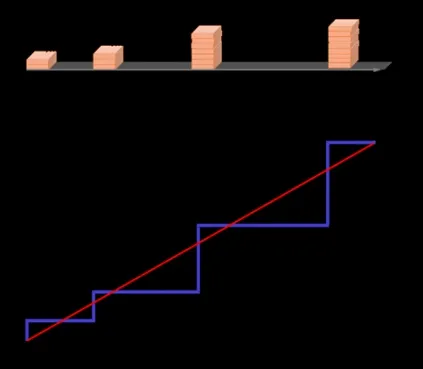
图1 能量因果性限制条件下的最优通信策略

因此，在能量采集驱动模型中需要加入能量因果性限制条件（ECC：energy causality constraint）：使用的总能量不能超过目前所采集的总能量；传统通信中的最优策略因而无法实现。若进一步考虑存储所采集能量的电池的有限容量的影响，探求EH驱动无线通信的最佳策略显然将遇到许多新问题、新难点。

在这些新型限制条件下，文献[1]-[5]研究了点对点、BC、MAC、中继及干扰信道模型中 EH节点的最优传输策略问题。其中，点对点链路中EH节点在静态（时不变）及时变衰落信道中的最佳通信策略问题已进行了大部分的研究和探讨。而对其它多点网络模型的研究却还仅局限于单天线[10][11]及时不变信道等简单场景。另外，现有方法不具有良好的可扩展性，难以应用于多天线、多用户、时变信道下的通用场景。

本文分别研究了MIMO BC和MIMO MAC系统吞吐量最大化的最优（离线）传输策略。通过结合上下行对偶性并引入“嵌套凸优化”方法，我们证明了本文的最优MIMO BC调度问题能转化为等效的“点对点”链路最优功率分配的凸问题，再通过凸优化理论得到MIMO BC系统中的原问题的最优解。

与只有一个能量采集驱动发送端的点对点广播通信情况不同，MAC中有多个发送端通过多址接入系统收集能量，而这些多个能量采集过程会对用户的传输策略产生耦合影响，因此，针对MAC系统提出了一个“阻塞协助提升迭代算法”来避开这些耦合影响，在每次迭代过程中通过固定部分用户的能量来获得某一个用户的最优功率分配值，进而将相应的问题也转化为类似BC中等效的“点对点”链路最优功率调度问题，从而可通过具有线性计算复杂度的基于注水的“绷弦算法”来获得原问题的解。连续的通过优化其他用户的功率分配，不断增加总的吞吐量，即能保证我们提出的方案收敛到一个全局最优功率分配解，从而获得全局最优MIMO MAC策略。

1 广播信道模型

考虑一个通用MIMO BC系统，在发送端有Nt根发送天线，K 个用户中每个用户都有 Nr根接收天线。表示从第发射端到第个用户的信道协方差矩阵，则用户k接收的复基带信号表达式如公式（1）：

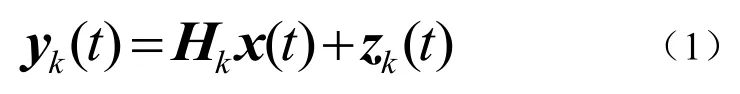
其中x(t)表示在时刻t的发送矢量信号表达式，zk(t)为附加零均值复高斯噪声信号表达式，其相应的Nr天线数量相关矩阵为I。发送的信号为信号发送到单独用户的求和，即(t 。总的发送相关矩阵则为，其中半正定为用户k的发送相关矩阵。总的发送功率为其中tr(·)为迹运算。

假定发送端为理想状态信息的信道，MIMO BC的信道容量可以通过脏纸编码（DPC ：dirty paper coding）获得，则在该编码中所有用户均可连续编码使得被编码的用户对已编码用户没有干扰影响。令则对于给定的发送功率P ，通过DPC得到的MIMO BC的容量区域为公式（2）：

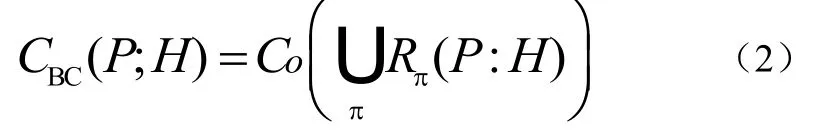
其中表示凸包，该集合包含所有用户指数集的排列，而

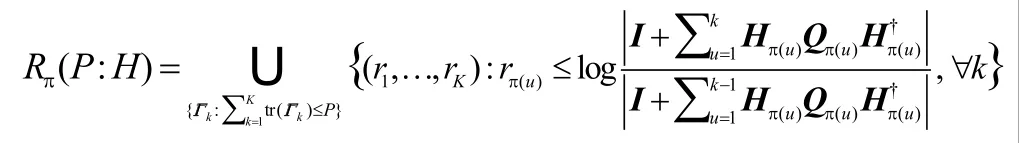
1.1 上下行链路对偶性

根据上下行对偶性，MIMO BC的加权吞吐量最大化可转化为相同总功率限制下如图2所示：

图2 MIMO广播信道与其对偶多址接入信道

其“对偶”MAC的加权吞吐量最大化问题。

在对偶MAC中，接收信号表达式如公式（3）：

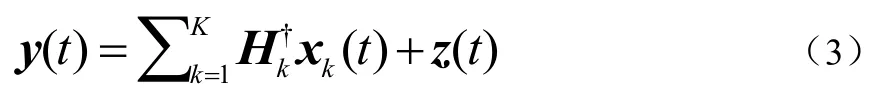
其中 xk(t)表示用户k在时刻t的发送矢量信号表达式，z(t)为附加零均值复高斯噪声信号表达式，其相应的Nr天线数量相关矩阵为I。表示用户k的发送相关矩阵，为K个用户收集的能量集。令，则对于给定的P，MAC容量区域为公式（4）：

在文章[8]中的上下行对偶性证明了公式(2)中BC容量区域等效于 MAC中满足所有功率矢量条件下容量区域的联合，即公式（5）：

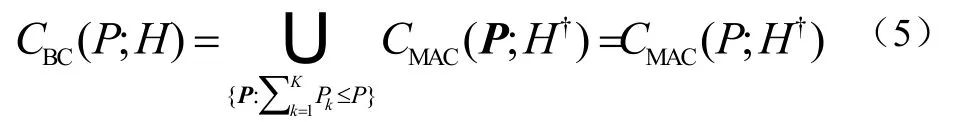
1.2 能量采集驱动过程

假定发送端没有持续的功率供应。取而代之的是通过嵌入的可收集能量装置机器和可充电电池，从而提供发送端从外界环境中收集到可再生能源并存储到电池中供后续使用。在初始时刻(t0=0)可利用能量为E0。在整个传输阶段[0, T]，假定有 N-1能量分别在时刻到达。为方便起见，表示两个连续的能量到达时刻间隔，称为时元。则第i个时元的长度为 Li=ti-t-1i， i=1,…,N 。很明显可以得到0＜ Ei≤Emax，i =0,1,…, N - 1, k=1,…, K否则超出的能量 Ei-Emax不能储存到电池里，所以可以取值到

1.3 理想情况下传播

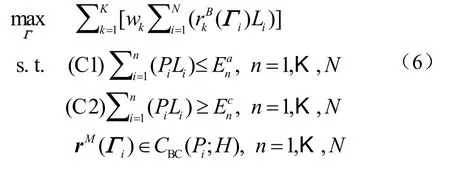
其中C1表示能量因果性限制，即目前累计消耗的能量不能超过累计采集的能量，C2表示最少能量使用限制，即目前累计消耗的能量需要达到一定的量，防止能量溢出。

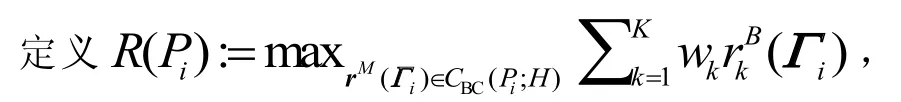
根据上下行对偶性，我们可证明：

引理1：严格凹函数 R(Pi)可通过以下凸函数问题的最优值来获得如公式（7）：

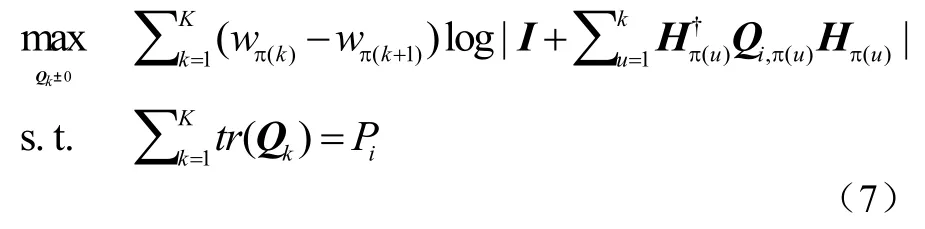
其中 π是用户 {1…,K,的指数排列：

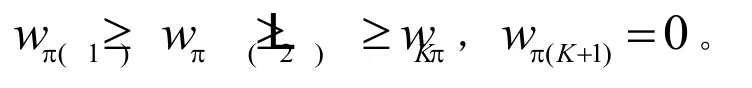
则可用 R(Pi)将最优广播问题转化为等效“点对点”链路的最优总功率分配问题如公式（8）：

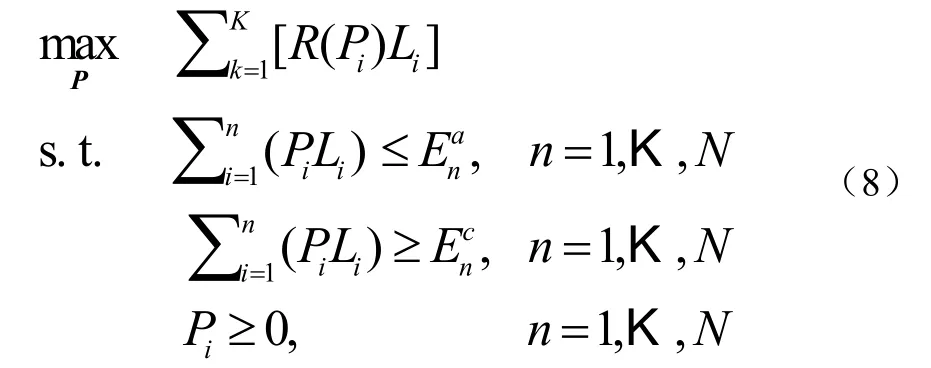
当EN=Emax时，tN时刻的最少能量使用限制条件和因果性限制条件会使得，即所有收集到的能量都必须在最后使用完。

1.4 凸优化及最优条件

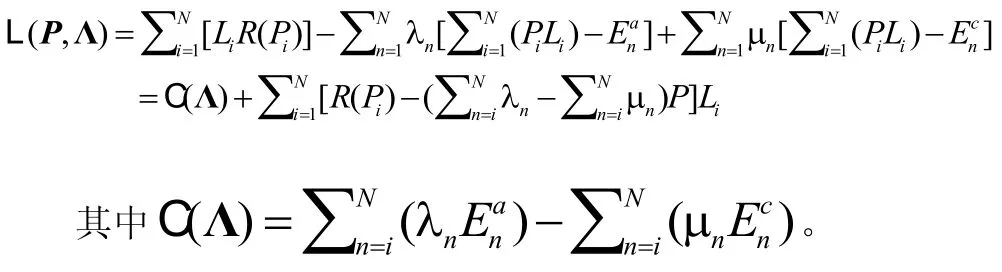
若用P*表示方程(8)的最优解，Λ*表示对应的最优拉格朗日乘子。定义。根据Karush-Kuhn-Tucker (KKT)最优条件[7]，可得：∀i，公式（9）

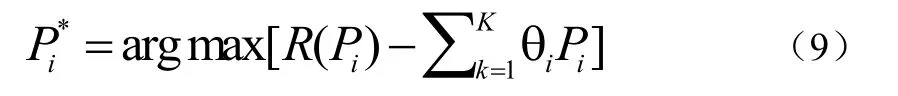
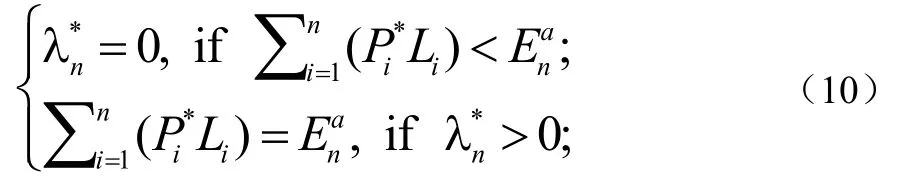
1.5 最优用户功率分配

在引理1已证明 R(Pi)为严格凹函数，令 R'(Pi)表函数 R(Pi)的偏导数，很显然， R'(Pi)是关于 Pi的严格递减函数。令 R'-1表示 R'的反函数，由方程(22)可得到考虑函数R(Pi)的严格凹性， R'-1(Pi)关于 Pi严格递减。因此，也为关于θi的递减函数，再根据方程(10)-(11)的互补松弛条件，我们能推断：

引理2：最优功率 P仅在某时刻tn（如能量因果性限制条件或最少使用限制条件收紧处）发生改变。特别地，若在时刻tn处则该时刻过后功率会增大；若在时刻tn处则该时刻过后功率会减小。

算法1基于绷弦功率算法

算法1的核心部分是FirstChangeP函数，该函数表示在系统的最优方案中，第一次功率改变时刻tτ、在该时刻之前使用的功率P，以及该时刻前消耗的总能量E。在该函数中，τ+和τ-为第一次时刻发生改变的两个候选时元指数，而P+和P-则分别表示维持在时元段和的候选功率。

1.6 在线算法探索

假定时不变信道H已知，收集能量过程通过随机泊松分布模拟，其中在时域T内到达的能量数服从均值为λe的泊松分布，而该能量数在每次到达时都是独立同分布的，均值为[9]。假定λe和已知。

为了确定算法1中t0=0时刻最优总功率的值，我们需要计算出每个 tn时刻和的值。调用，其中当初始能量 E0已知时，所有的 Ei,i = 1,… ,n-和 Li,i = 1,…,n都是未知的信息，在实际中是很难预先知道的。即表示为在时间段(0, tn)收集的总能量，其中。给定λe和，可得公式（14）：

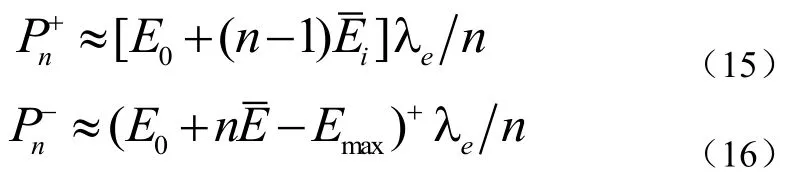
利用公式(15)-(16)中的估计值，我们将同算法1一样应用功率绷弦方法产生在t0时刻第一个发送功率值，这些功率一直使用到新的能量到达时刻t1，接着我们将把t1当做新的“t0”，并将初始能量E0更新为未消费的新收集能量E1。依据公式（15）-（16），再次执行算法来产生下一个发送功率值。该过程一直持续到所有能量用尽或到达传输时段T末端。

2 多接入信道模型

根据第2节提出的上下行对偶MIMO MAC系统。假定每个用户通过独立的能量采集过程补充功率，令用户k的电池容量为Emax,k，在初始时刻(t0=0)可利用能量为E0,k。在整个 传输阶 段 [0T, ，假定 有 N-1能量分别在时刻到达。目标方程为最大用户吞吐量权重和如公式（17）：

引理3：严格凹函数 R(Pi)可通过以下凸函数问题的最优值来获得公式（18）：

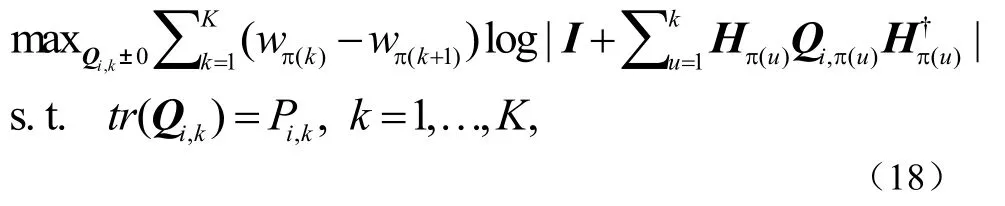
则可用 R(Pi)将公式(17)转化为以下功率分配问题如公式（19）：

同理可将方程(19)转化为一个凸问题。根据凸优化理论，最优解 Pi*和最优拉格朗日乘子 Λ*的充分必要最优条件为：

以及：∀n,∀k，如公式（21）、（22）

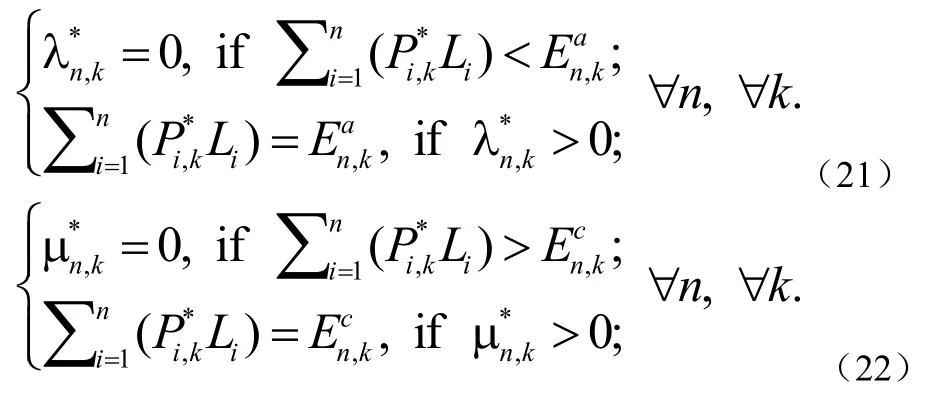
由于R(Pi)给出的不是封闭解，通过一般的解凸优化方程法很难找到满足方程（20）-（22）的关于方程（19）的全局最优解 {}。依据方程（20）-（22）的特殊结构，我们将提出一个低复杂度的阻塞协调提升算法来获得{}。

2.1 最优用户功率分配

与点对点广播传输不同的是，在MAC信道中，每个用户都有其独立的能量因果性限制和最少使用限制集，而这K组能量采集限制集在最优用户传输策略中又有着相互的耦合影响。为了绕开该耦合带来的困难，我们将采取一系列凸优化方式，如：每次迭代过程中我们通过固定用户k以外的所有用户的功率来求得单个用户k的最优功率分配值。

若用Pi,-k表示功率集 Pi中用户k以外所有用户的功率集，则可得。令q表示迭代指数，而和，分别为Pi,k和拉格朗日乘子在第q次迭代中的最优值。在功率计Pi,-k固定的条件下，可由方程（20）得到公式（23）：

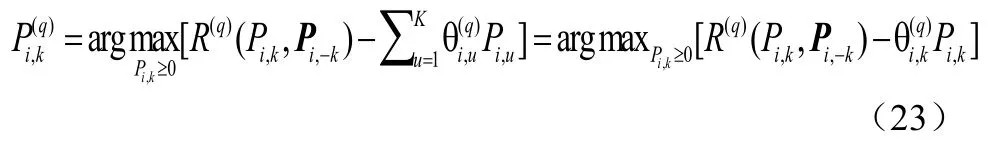
同理，由方程（21）-（22）可直接得到公式（24）、（25）：

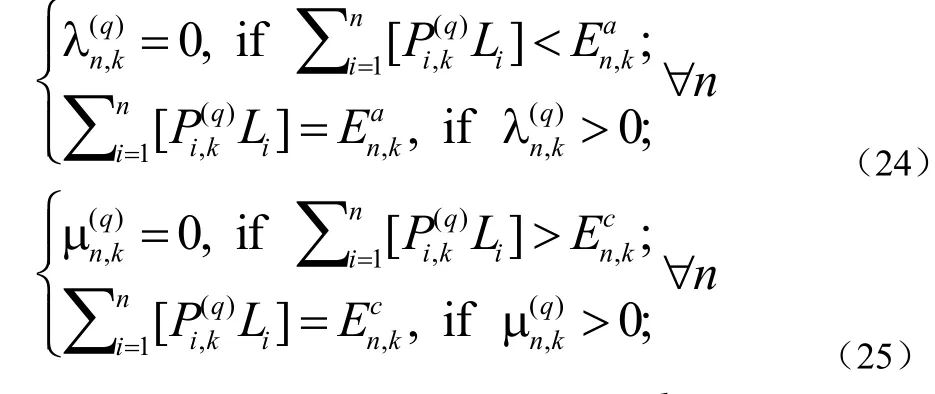
公式（23）-（25）正好对应于在用户k与接收点之间的等效“点对点”链路总吞吐量最大化问题的KKT条件。而第二节中的低复杂度“绷弦”算法可以用来获得 {}。如果考虑其他用户发送的信号，可归为在优化MIMO MAC编码中的噪声。因此，尽管本模型中MIMO MAC物理信道是时不变的，但该等效的“点对点”链路的结果是通过固定其他用户的功率值来获得的，而在每次迭代过程中，其他用户由于其不同的信号功率可能会引入不同的噪声水平，因而该信道实际上也是“时变”的。固我们应该采用一个基于“绷弦”的水柱算法来找到 {}。

引理4：1) 用户k的最优功率值{}解的形式可由注水形似给出：，其中注水因子

基于引理 4揭示的内容，我们将进一步提出一个基于“绷弦”注水算法。令和分别表示：在第q次迭代中，使得用户k在tn时刻时隙n的能量因果性限制条件和最少使用限制条件收紧的注水因子常量。给定时刻tn之前的注水因子ω，而为给定的在时隙i中用户k的功率。因此，对的值能通过以下方程解出公式（26）：

算法2基于绷弦注水算法

同理算法2中的FirstChange函数表示第一次水柱改变时刻tτ及在该时刻之前使用的注水因子（与算法1中的功率P相对应）。两个候选的注水因子将以的形式更新。

2.2 阻塞协调提升迭代算法

算法3阻塞协调提升迭代算法

算法3中的每第q次迭代，都将调用算法2中的基于绷弦的注水算法，连续的一个接一个优化用户发送功率。根据，再逐次通过引理3的方法计算出方程(18)中的 R()，进而求出总吞吐量并和上一次迭代求出的总吞吐量进行比较，直到吞吐量的增量小于容忍度时迭代终止。由于算法3实际上服从经典的阻塞协调提升思想，所以它能收敛到一个局部最优。因为公式(19)是一个凸问题，则每一个局部最优都将是全局最优，即算方法3将使公式（19）收敛到一个全局最优的 P*。一旦获得 P*，再通过公式（18）和≡,∀i ,k,我们将最终找到MIMOMAC中最优发送相关矩阵{}。

2.3 在线算法探索

用解耦“功率绷弦”方法得到近似最优结果，该思路激励我们提出一个探索式的在线方案。假定时不变信道H已知，每个用户收集到的能量通过随机泊松过程模拟，其中在时域T内到达的能量数服从均值为λe的泊松分布，而该能量数在每次到达时都是独立同分布的，均值为。假定λe和已知。当初始能量 E0,k,∀k已知时，所有的都是未知的信息，在实际中是很难预先知道的。则公式（27）、（28）：

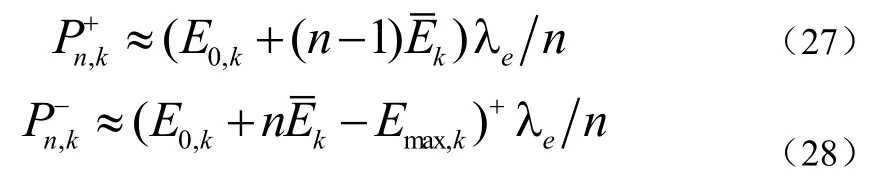
3 仿真结果

设定一个只有K=2用户的时不变MIMO BC，数据传输时长T=100s。权重矢量w=[1,1]，在信道矩阵Hk(k=1,2)中的每一个元素都是零均值复高斯随机变化的单位变量。发送端的电池容量为 Emax= 100焦耳。假定发送端随机能量采集过程的设定可通过一个均值同为λe的随机泊松过程来模拟，每次能量到达的数量服从均值为50焦耳独立同分布。

平均吞吐量与λe如图3所示：

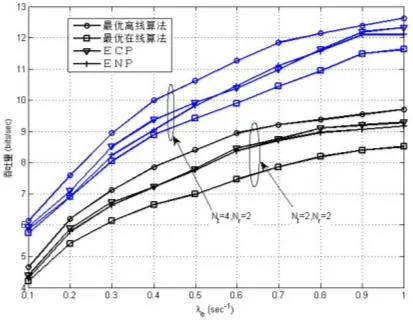
图3 BC中不同能量达到概率λe下平均吞吐量

在分别设定（Nt, Nr）为（2,2）和（4,2）时的对比情况，每一组结果都是取50次随机产生实验情况的平均值。图3中加入了离线最优功率绷弦算法和提出的在线方案，为了进行对比，我们还加入对比了两组其他可行方案：满足因果性方案（ECP：energy causality policy）和最少能量使用方案(ENP：energy non-overflow policy)，这两组方案分别是通过总是选取发送功率满足其下一组因果性和最少能量使用限制条件来获得。提出的离线最优算法在所有λe值下都能取得理想的吞吐量值，也明显优于在线最有算法。图3中也很明显看出当发送天线数量增倍时，MIMO BC的总速率也显著提升了。

在设定（Nt, Nr）为（2,2），λ=0.1,0.2,0.3,0.4时，算法2在每次迭代后的平均吞吐量如图4所示：

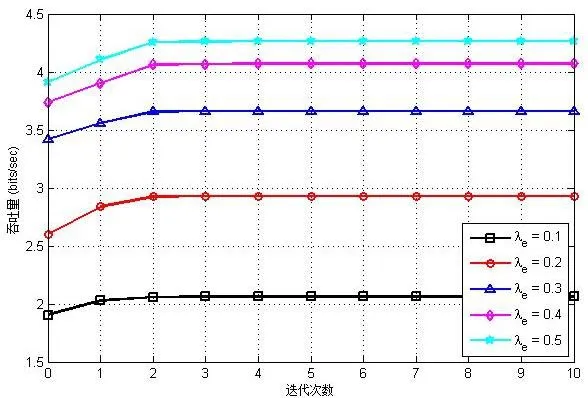
图4 吞吐量与迭代次数

则算法2的快速收敛性显而易见，经过3到4次迭代之后就能收敛到最优值。

不同方案下平均吞吐量与λe的对比情况，如图5所示：

图5 MAC中能量到达概率λe下平均吞吐量

其中每一组结果都是通过40次随机产生试验次数来获得的。我们比较了算法4和解耦的功率绷弦方案的性能，同时我们也加入对比了ECP和ENP方案。从图5中我们也能有趣的发现，对于解耦的功率绷弦方案，每个用户只需要其能量采集信息，就能获得接近最优吞吐量基准值99%的结果。另一方面，满足因果性方案和非溢出方案在已知下一组（非因果）能量到达信息条件下也能获得较优的吞吐量值，而相比最优基准值会有接近0.3比特/秒的相差量。本文提出的在线方案尽管仅知每个用户所需的因果信息，但在所有λe情况下也能获得接近最优总吞吐量85%的好结果。

4 总结

本节提出了一个新颖的算法来获得MIMO BC和MIMO MAC在有能量采集驱动的理想电路环境下最优传输方案。该方案能以低复杂度计算离线最优解，能为未来无线通信网络中带能量采集驱动的数据传输实践案例提供最优基准参考。文中也提出了基于最优策略的在线方案。

[1]Yang J. and Ulukus S., Optimal packet scheduling in an energy harvesting communication system[J].IEEE Trans. Commun., 2012,60(1):220-230.

[2]Ho C. and Zhang R.Optimal energy allocation for wireless communications with energy harvesting constraints[J]. IEEE Trans. Signal Process,2012,60(9):4808-4818.

[3]Ozel O., Jing Y., Ulukus S.Optimal broadcast scheduling for an energy harvesting rechargeable transmitter with a finite capacity battery[J]. IEEE Trans. Wireless Commun.,2012,11( 6):2193-2203.

[4]Yang J. and Ulukus S.Optimal packet scheduling in a multiple access channel with energy harvesting transmitters[J]. J. Commun. Netw,2012,14(2):140-150.

[5]Tutuncuoglu K. and Yener A.The energy harvesting multiple access channel with energy storage losses[J]. Proc. ITW, 2012.

[6]Tutuncuoglu K. and Yener A. Optimum transmission policies for battery limited energy harvesting nodes，”[J].IEEE Trans. Wireless Commun.,2012, 11(3):1180-1189.

[7]Yang J. and Ulukus S.Optimal packet scheduling in an energy harvesting communication system[J].IEEE Trans. Commun.,2012, 60(1):220-230.

[8]Vishwannath S., Jindal N., and Goldsmith A.Duality. Achievable rates, and sum rate capacity of Gaussian MIMO broadcast channels[J]. IEEE Trans. Inf. Theroy, 2003,49(10):2658-2668.

[9]Xu J. and Zhang R.Throughput optimal policies for energy harvesting wireless transmitters with non-ideal circuit power[J]. to appear in IEEE J. Sel. Areas Commun..

[10]Boyd S. and Vandenberghe L., Convex Optimizatio[M], Cambridge University Press,2004.

[11]Zafer M. and Modiano E..A calculus approach to minimum energy transmission policies with quality of service guarantees[J]. Proc. INFOCOM,2005, 1:548–559.

Optimal Transmission Policy for Energy-harvesting Powered MIMO Broadcasting and Multi-access Channels

Li Wenming
(Department of Communication Science and Engineering, Fudan University, Shanghai 200433, China)

This paper develops a novel approach to obtain optimal transmission strategy for the energy-harvesting node. With convex optimization tools, it explores optimal transmission for MIMO BC and MIMO MAC network models, and provides a low-complexity uplink-downlink duality “nested optimization” method and iterative block coordinate ascent algorithm to obtain the optimal transmission policies that maximize the weighted sum-throughput, and it researches their online implementations for practical energy harvesting communication systems. The proposed approach will provide theoretic guidelines for practical designs of the future energy-harvesting MIMO BC and MIMO MAC communication networks.

Energy Harvesting; BC; MAC; Power Control; Convex Optimization; Iteration

TN919.1

A

2014.06.05）

1007-757X(2015)05-0054-07

李文明（1989-），男，湖北，复旦大学通信科学与工程系，硕士研究生，研究方向：无线通信网络中的能量收集，上海，200433