Ramsey数和无三角的Cayley图

厉明波，李雨生

（同济大学 数学系，上海200092）

设H是一个加法群，H＊＝H＼｛0｝.一个H的子集A被说成是关于逆元封闭的，是指若x∈A，则－x∈A.对一个H＊逆元封闭的子集A，可定义一个图GH（A）如下：它的点集是H，而｛x，y｝是一条边当且仅当｜x－y｜∈A.图GH（A）被称为由A导出的Cayley图.

本文里，群H是Zn＝｛0，1，…，n｝，即模n的整数加群.对于Zn的一个逆元封闭子集A，简记由A生成的Cayley图GZn（A）为Gn（A）.因Zn中x的逆元是n－x，故｛x，y｝是Gn（A）的一条边当且仅当｜x－y｜∈A.有两个平凡的Gn（A），其一是空图，对应的生成集A＝Ø，其二是圈Cn，对应的生成集A＝｛1，n－1｝.下面的性质是熟知的，参见文献[1].

引理1 设A⊆Z＊n为逆封闭子集，则Gn（A）是点传递的，且点i的邻域是

A＋i＝ ｛a＋i：a∈A｝

特别地，Gn（A）是｜A｜－正则的；Zn的任何子集S是一个独立集当且仅当对S中任何两个相异的元x和y都有｜x－y｜∉A.

设m和q为正整数，定义Ramsey数r（m，q）为最小的正整数n使得任何阶为n，不含Km的图都有q元独立集.以α（G）记图G的独立集.当Gn（A）不含三角形且α（Gn（A））≤q，则r（3，q＋1）≥n＋1.Ramsey理论的发展，参见文献[2].

集合A⊆Zn被说成是无和的，是指（A＋A）∩A＝Ø就是说，方程x＋y＝z在A中无解，这里x，y，z不必两两互异.显然，无和集不包含零元素.计算将依据下面的结果.

定理1 设A，A′都是Z＊n中的逆元封闭子集.则有

（1）若A′⊆A，则Gn（A′）是Gn（A）的一个子图，此时α（Gn（A′））≥α（Gn（A））.

（2）Gn（A）不含三角形当且仅当A是无和集.

（3）若A是无和集，则α（Gn（A））≥｜A｜.

证明 设A′⊆A，若｛x，y｝是Gn（A′）的一条边，则｜x－y｜∈A′故｜x－y｜∈A，从而｛x，y｝是Gn（A）的一条边.即Gn（A′）是Gn（A）的一个子图，（1）得证.

为证明（2），先假定A是无和集，要证明Gn（A）不含三角形.显然，一个图不含三角形当且仅当它的任何邻域不含边.由引理1可知，Gn（A）是点传递的，点0的邻域就是A.故要证Gn（A）不含三角形，只要证明A中任何两点不相连.当A只含一点，这是平凡的.否则设A＝｛x，y，…｝，其中x≠y.若x和y相连，｜x－y｜∈A，故存在z∈A使得x－y＝z或y－x＝z，等价于x＝y＋z或y＝x＋z，与A为无和集的假设矛盾.

另一方面，假定Gn（A）不含三角形，则点0的邻域A不含任何边.证明A是无和的.若x＋y＝z在A中有解，则显然x≠z，这是由于A是的子集.同理y≠z.

情况1x＝y≠z.此时，有2x＝z，得x＝z＋（n－x），其中n－x∈A（因A对逆元封闭）.此时互异的三个元素0，z，n－x组成一个三角形，矛盾.

情况2x，y，z互异.此时，有z－x＝y∈A，得｜z－x｜＝y∈A或｜z－x｜＝－y∈A，故｛x，z｝是一条边，而互异的三个元素0，x，z组成一个三角形，矛盾.

为证（3），设A是无和集.由（2）已知，Gn（A）不含三角形，因此点0的邻域A没有边，从而A是一个独立集，故α（Gn（A））≥｜A｜.

设Φ是一个集合族.其中A0∈Φ说成是最大的，是指A0所含元素是Φ中最多的，它被说成是极大的，是指若A0不可能是Φ中任何集合的真子集.显然最大集必然是极大集，但极大集不必是最大集.可得下述推论.

推论 设Φ是的所有逆元封闭的无和集所成的集合族，且A0∈Φ使得

α（Gn（A0））＝ min｛α（Gn（A））：A∈Φ｝

则A0是极大的；且Gn（A0）不含三角形.故r（3，q＋1）≥n＋1，其中q＝α（Gn（A0））.

定理1及其推论并没有肯定有一个最大无和集A产生的Cayley图Gn（A）有最小的独立数.例如，若n≥4是一个偶数，A＝｛1，3，…，n－1｝，则A是逆元封闭的且无和的，而Gn（A）＝Kn／2，n／2是一个平衡的完全二部图，故α（Gn（A））＝n／2，其独立数很大.然而，由定理1及其推论可知，对于固定的n，在寻求由最小独立数的Gn（A）的过程中，只要考虑那些极大（不仅是最大）的逆元封闭的无和集即可，这将节约计算机运算时间.

将计算一些较小阶的不含三角形的Cayley图的独立数，在同样阶的此类图中，选择那些独立数最小的图，从而获得新的Ramsey数r（3，q）的下界，这些结果被列于表1中.改进了r（3，q）的下界，27≤q≤38.那些被改进的下界分别在文献[3－5]获得.对于Ramsey数的这些结果，可以参考文献[5].

表1 当27≤q≤38时r（3，q）新下界Tab.1 New lower bounds for r（3，q）with 27≤q≤38

算法主要步骤如下：

第一步，给定正整数n，搜索极大的逆元封闭的无和集A⊆Z＊n，计算α（Gn（A））；发现A使得α（Gn（A））达到最小.

第二步，加大n，重复第一步.

本文使用约束传播算法.由于约束的限定，大大提高了搜索的速度.其中的一个约束选取的元素是无和的，另外一个约束选取的元素的个数不能大于设定的最大值.

在确定一个生成集A之后，运算时间的主要部分是计算α（Gn（A））.其中对于n＝258，用于发现最小α（Gn（A））和相应的A，用时超过一周.本文用子图同构来计算最大独立数，可以提高计算最大独立数的速度，值得进一步研究.

计算结果见表2.在相同独立数的Cayley图Gn（A）中，本文仅列举了n最大时的计算数据.在这些表中，第一行是Gn（A）的阶数n，其为有相同的独立数的最大n；第二行是相应的生成集A，它是逆元封闭且无和的；第三行是独立数α（Gn（A））.

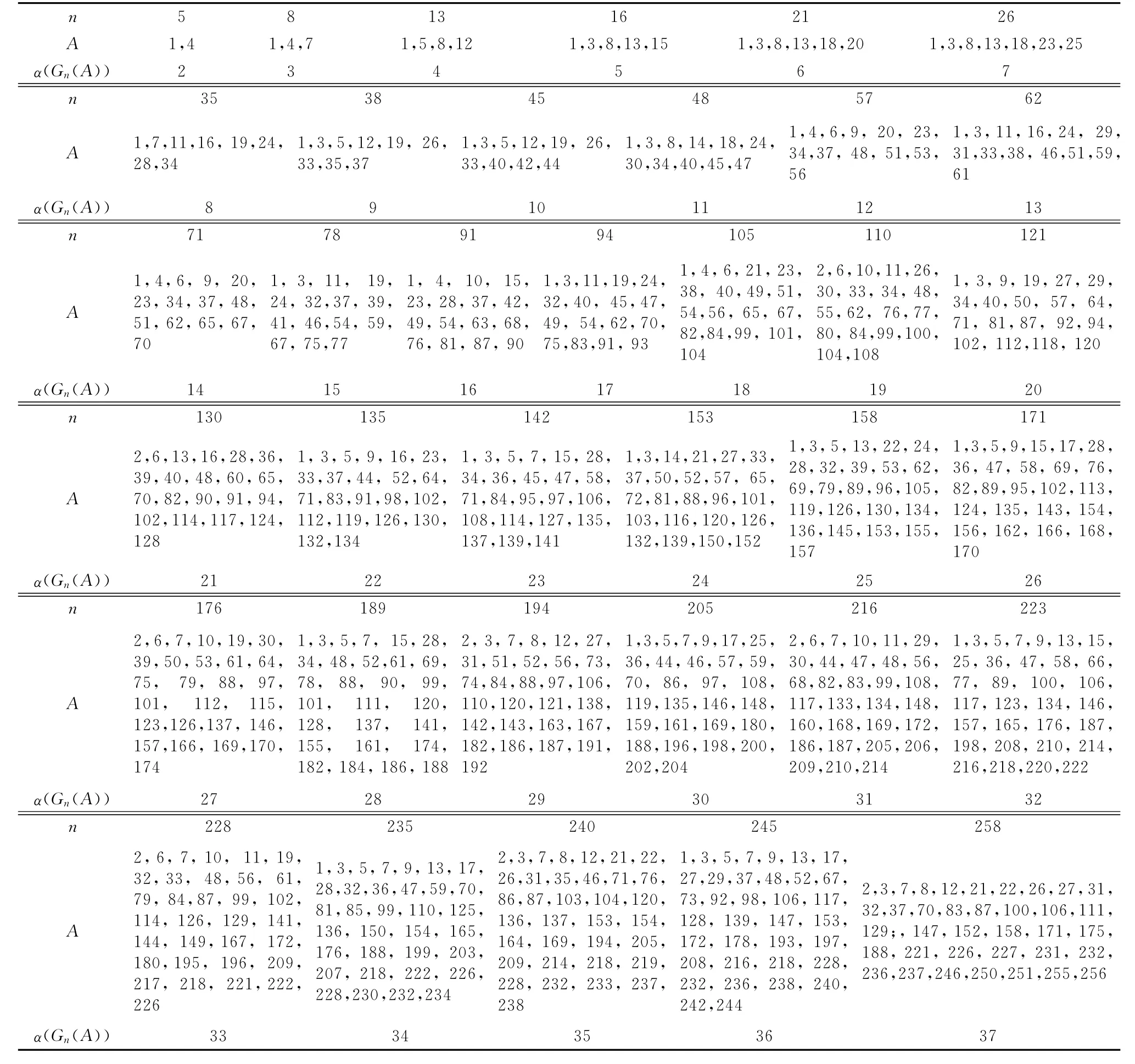
表2 集合A 和α（Gn（A）），2≤α（Gn（A））≤37Tab.2 Sets A andα（Gn（A））with 2≤α（Gn（A））≤37

[1] Godsil C，Royle G.Agebraic graph theory[M].Berlin：Springer，2001.

[2] Graham R，Rothschild B，Spencer J.Ramsey theory[M].New York：John Wiley ＆Sons，1990.

[3] Wu K，Su W，Luo H，et al.New lower bound for seven classical Ramsey numbers R（3，q）[J].Appl Math Lett，2009，22：365.

[4] Wu K，Su W，Luo H，et al.A generalization of generalized Paley graphs and new lower bounds for R（3，q）[J／CD].Electron J Combin，2010.

[5] Chen H，Wu K，Xu X，et al.New lower bound for nine classical Ramsey numbers R（3，t）[J].Journal of Mathematics，2011，31：582.