轴向柱塞泵滑靴副热平衡间隙及影响因素分析

汤何胜，李 晶，訚耀保

（同济大学 机械与能源工程学院，上海201804）

轴向柱塞泵是工程机械上的液压驱动设备之一，随着液压驱动设备需求增大，摩擦副的润滑失效问题已成为制约轴向柱塞泵性能的主要障碍.在轴向柱塞泵中，滑靴副是一对非常关键的摩擦副，该摩擦副是完成轴向柱塞泵的吸油和排油等工作过程的重要部件，也是轴向柱塞泵润滑失效的关键环节.其中，滑靴与斜盘之间的间隙油膜可避免金属之间发生接触摩擦，但在实际工况下，间隙油膜因压差和剪切流动产生黏性耗散，油膜厚度减小，促使滑靴发生黏着磨损，对滑靴副润滑特性产生显著的影响[1].柱塞泵摩擦副的研究主要集中在流体润滑机理和金属表面磨损特征领域[2－3]，而对其热力学特性的研究则相对较少.Wieczorek等[4]围绕摩擦副油膜动力学和能量耗散开展研究，对间隙油膜厚度和功率损失进行预测.Koc等[5]分析倾覆状态下滑靴的压紧力系数、偏心载荷及阻尼孔结构等参数对油膜润滑特性的影响.Johnson等[6]采用试验法对不同滑靴球窝结构下油膜微观特性展开研究，分析不同滑靴结构对油膜动力学特性的影响.Kazama[7]分析绝热和等温条件下柱塞泵滑靴副油膜厚度和温度变化特征.Bergada，Kumar等[8－9]利用计算流体力学（CFD）技术分析滑靴环形密封槽内流体的静动态特性，讨论不同工况下环形槽内流体的流动特征和涡流效应.目前国内学者对柱塞泵滑靴副油膜润滑特性进行了研究并取得一些有益的结论.文献[10－11]根据能量守恒定律建立柱塞泵的热力学模型，分析摩擦副间隙油液温升变化规律.文献[12－14]围绕轴向柱塞泵滑靴副油膜润滑特性开展研究，解释滑靴倾覆的本质以及能量耗散的原因.然而，大多数研究没有考虑流体介质与固体之间的热传导作用对滑靴副油膜润滑特性的影响.因此，本文考虑滑靴、斜盘以及油膜的热传导关系，结合能量守恒定律，建立滑靴副热平衡间隙数学模型，分析滑靴副热平衡间隙的变化特征.

1 滑靴的静压平衡原理

图1所示为轴向柱塞泵结构图.当缸体随主轴旋转时，在0～180°范围内，柱塞腔的容积不断减小，促使液压油从配流盘的排油槽流出，这是排油过程.在180～360°范围内，柱塞沿缸体向外伸出，柱塞腔的容积不断扩大，将油液从配流盘的吸油槽引入柱塞腔内，这是吸油过程.为了减小滑靴底部接触应力，滑靴的结构设计采用静压平衡方法.通过滑靴的阻尼管将柱塞腔的压力油引入滑靴的中心油腔，使其产生的液压支承力与柱塞腔的压紧力相互平衡.

图1 轴向柱塞泵结构图Fig.1 Structure of axial piston pum p

2 滑靴副热平衡间隙模型

2.1 滑靴副的热传导模型

由于间隙油膜、滑靴以及斜盘存在热交换，满足能量守恒定律，将间隙油膜等效为控制体，利用热力学第一定律建立开放式热力学模型.图2所示为滑靴副油膜控制体模型.该模型可以与外界进行热交换，同时可以输入或者输出轴功，控制边界可以移动，则间隙油膜的能量守恒方程为

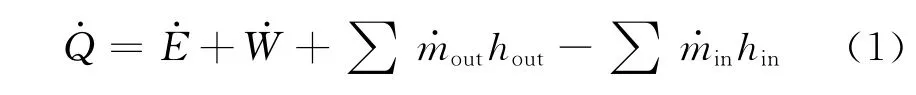
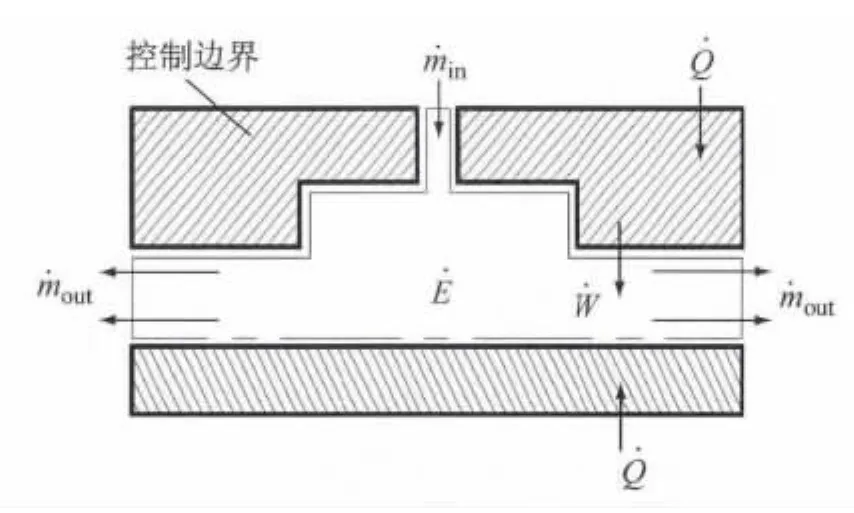
图2 滑靴副油膜控制体模型Fig.2 Control volume model of oil film in slipper pair

单位时间控制体内能量的变化率可表示为

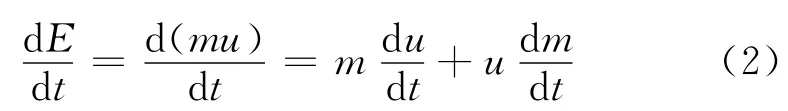
式中：u为流体的比内能.

流体的焓定义为

式中：ps为滑靴的中心油腔压力；υ为流体比容.

滑靴的中心油腔压力与柱塞腔压力以及滑靴的结构参数有关，其表达式为[15]

式中：p为柱塞腔压力；l为阻尼管长度；d为阻尼管直径；R为滑靴外径；r0为滑靴内径；δ为滑靴的热平衡间隙.

单位时间内流体焓的变化率定义为

式中：T为油膜温度；cp为流体的比定压热容；αp为流体体积膨胀系数.

将式（5）带入式（2）可得

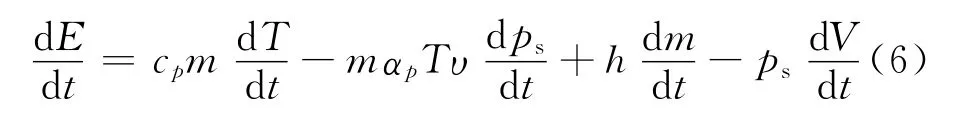
式中：V为控制体的体积.

单位时间内控制体的质量流量为

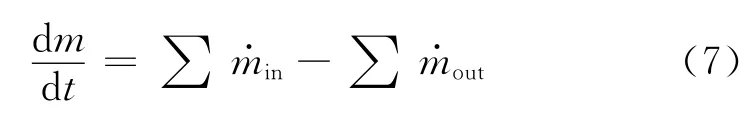
将式（6），（7）代入式（1）可得

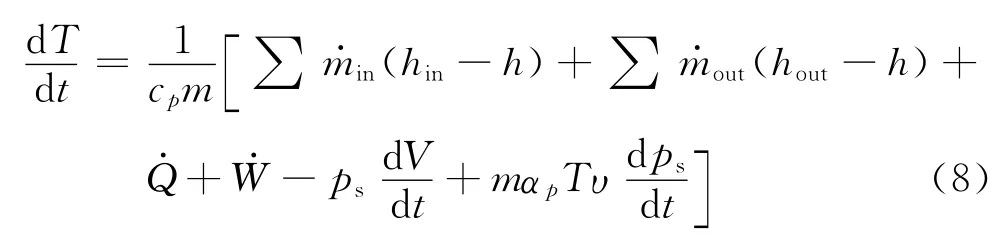
控制体做功的功率主要包括轴功和边界功.滑靴的功率损失源于泄漏流量和黏性摩擦.因此，油膜控制体做功的功率为

式中：s为轴功b为边界功.

轴功包括泄漏功率损失和黏性摩擦功率损失，

其表达式为

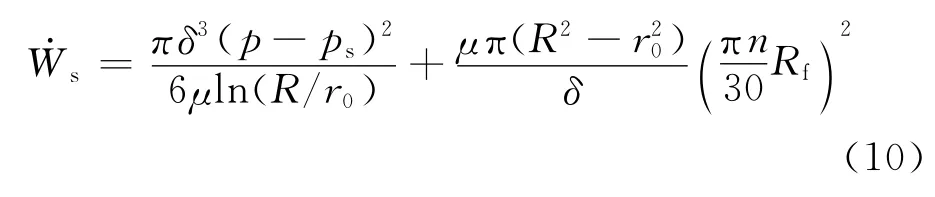
式中：μ为油液黏度；Rf为滑靴分布圆半径；n为缸体转速.

一般可以认为控制体内的流体焓值与出口的流体焓值相同[16].油膜控制体的输入能量和质量流量源于泄漏损失油液，将式（9）代入式（8）整理可得

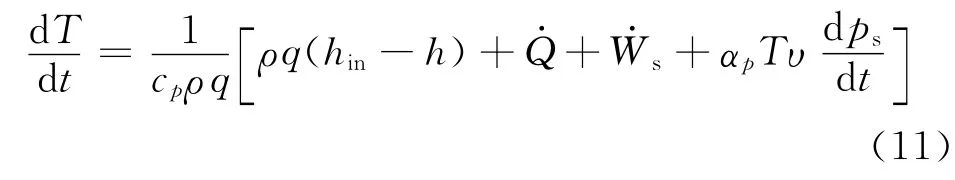
式中：ρ为油液密度；q为泄漏流量.

由式（4）可以得焓变化计算式为

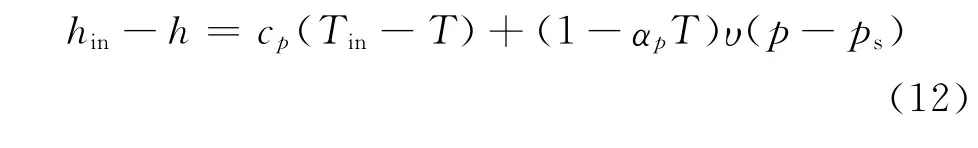
式中：Tin为进口油液温度.

将式（11）代入式（10）整理可得

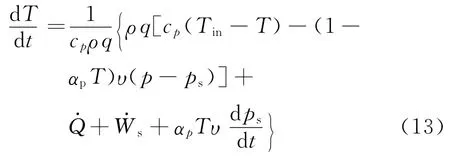
对于滑靴副而言，将油膜作为控制体，可利用式（13）对控制体内温度的动态特性进行计算.

2.2 滑靴副的热传导关系与热平衡间隙

滑靴由中心油腔和密封带所组成，为轴对称结构.图3为滑靴副的热传递过程.由于滑靴在半径方向上存在温度梯度，所以滑靴可以等效为环形圆柱模型.其次，滑靴因泄漏和黏性摩擦所产生的功率损失，全部转化为热能，引起油液温度升高，促使油膜、滑靴以及斜盘之间进行热交换.根据傅里叶定律和牛顿冷却定律，滑靴的中心油腔壁面和外缘壁面温度的关系为[17]

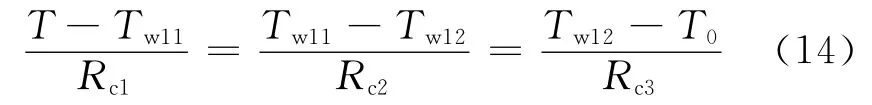
式中：T为油液温度；T0为壳体内腔油液温度；Tw11为滑靴中心油腔的壁面温度；Tw12为滑靴外缘的壁面温度；Rc1，Rc3分别为对流液阻；Rc2为传导热阻.Rc1＝（k02πr0H1）－1，Rc2＝ln（R／r0）／（k12πr0H1），Rc3＝（k02πRH1）－1，其中k0为油液的导热系数；k1为滑靴的导热系数；H1为滑靴材料的厚度.

因此，滑靴的热传导速率为

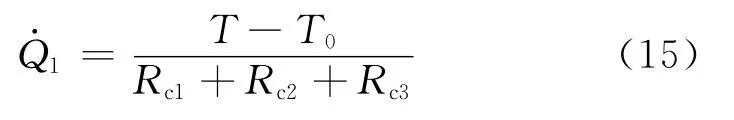
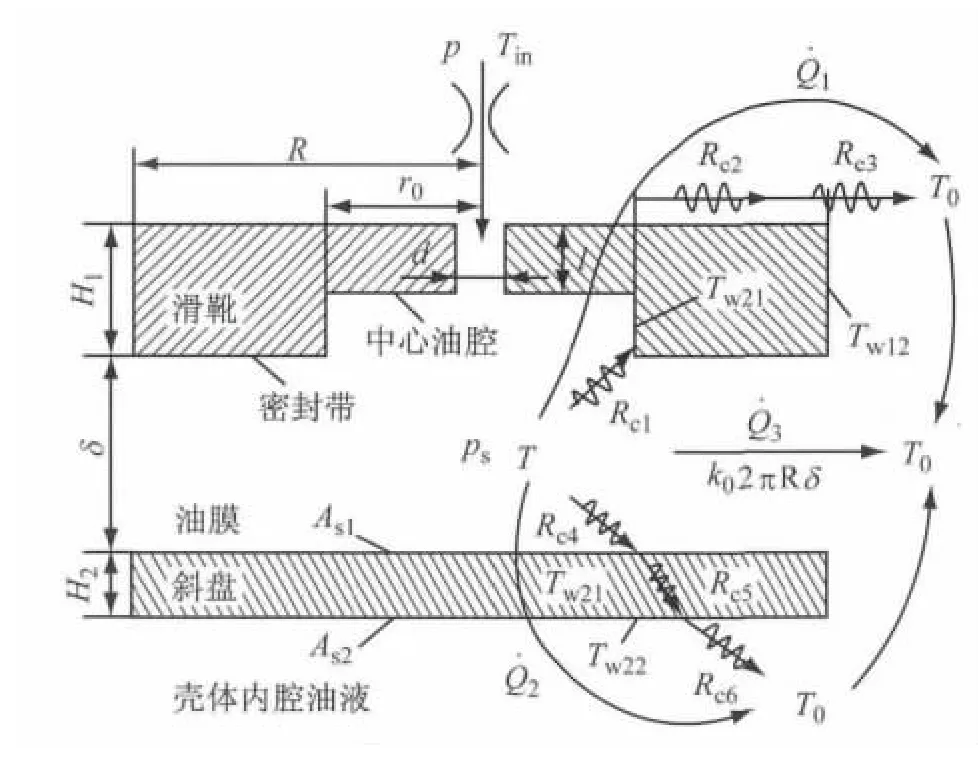
图3 滑靴副的热传递过程Fig.3 Heat conductivity process of slipper pair

斜盘等效为平行圆盘结构，斜盘的内侧和外侧壁面温度的关系为

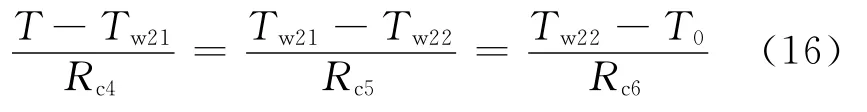
式中：Tw21为斜盘的内壁面温度；Tw22为斜盘的外壁面温度；Rc4，Rc6分别为对流液阻；Rc5为传导热阻.Rc4＝（k0As1）－1，Rc5＝H2／（k2As1），Rc6＝（k0As2）－1，其中，k2为斜盘的导热系数；H2为斜盘材料的厚度；As1为斜盘的内壁面传热面积；As2为斜盘的外壁面传热面积.

因此，斜盘的热传导速率为

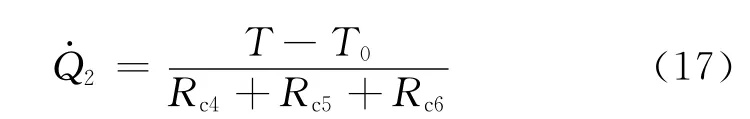
滑靴底面油液的热对流速率为

因此，油膜控制体的对流换热速率可表示为

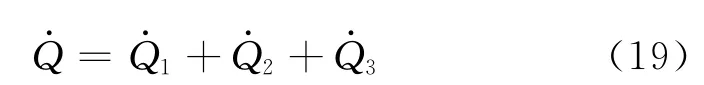
将式（19）代入式（13），计算间隙油膜的温升变化规律.根据滑靴和斜盘的热传递关系，计算滑靴与斜盘的温升.

（1）滑靴的温升表达式为

式中：ΔTw1为滑靴的温升；c1为滑靴的比热容；m1为滑靴质量.

（2）斜盘的温升表达式为

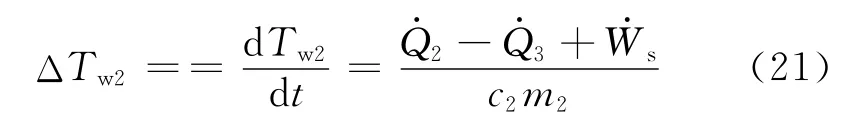
式中：ΔTw2为斜盘的温升；c2为斜盘的比热容；m2为斜盘的质量.

由于材料的线膨胀系数不同，导致滑靴副的热平衡间隙发生变化.因此，将式（20），（21）代入式（22），滑靴的热平衡间隙为

式中：h0为初始油膜厚度；α1，α2为线膨胀系数.

3 热平衡间隙影响因素分析

本节围绕滑靴副热平衡间隙进行理论计算，讨论柱塞腔压力、缸体转速以及进口油液温度对热平衡间隙的影响.本文计算所选用工况条件及参数如下：柱塞腔压力p＝21 MPa，缸体转速n＝1 500 r·min－1，滑靴外径R＝16.0 mm，中心油腔半径r0＝6.4 mm，阻尼管直径d＝1.0 mm，阻尼管长度l＝3.5 mm，分布圆半径Rf＝46.8 mm，导热系数k1＝92W·（m·°C）－1，黄铜的线膨胀系数α1＝18.8×10－6°C－1，密度ρ1＝8300 kg·m－3，材料厚度H1＝6.3 mm；斜盘材料密度ρ2＝7300 kg·m－3，导热系数k2＝54.4 W·（m·°C）－1，材料厚度H2＝26.8 mm，球墨铸铁的线膨胀系数α2＝11×10－6°C－1，油液的比定压热容cp＝1 884 J·（kg·°C）－1，导热系数k0＝0.26 W·（m·°C）－1，密度ρ＝860 kg·m－3，进口油液温度Tin＝50°C；初始油膜厚度h0＝4 μm.

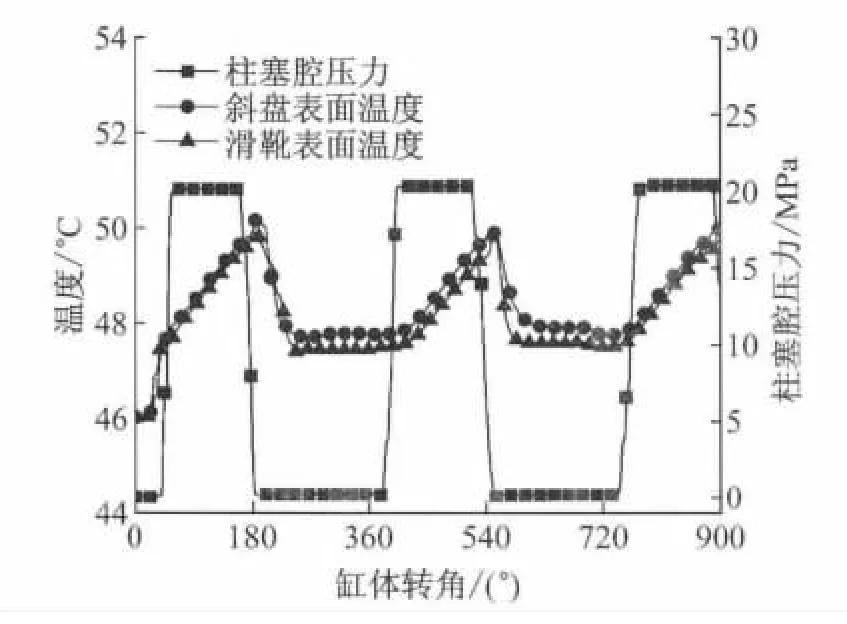
图4 柱塞腔压力对滑靴和斜盘表面温度的影响Fig.4 Effect of cylinder pressure on surface temperature of slipper and swashplate

图4为滑靴、斜盘的表面温度与柱塞腔压力之间的关系.滑靴和斜盘的表面温度随缸体转角呈周期性变化，当滑靴处于柱塞腔的排油区（0°～180°）时，滑靴和斜盘的表面温度呈线性递增关系，最高温度分别为49.5°C和50.0°C，出现在柱塞腔的吸排油过渡区，其原因是间隙油膜因压差和剪切所造成的功耗损失是油膜温度升高的主要原因，增大了滑靴和斜盘的热传导速率，引起滑靴和斜盘的表面温度升高.当滑靴处于柱塞腔的低压油区（180°～360°）时，滑靴和斜盘的表面温度呈线性递减关系，最低温度分别为47.1°C和47.4°C.滑靴和斜盘的导热速率随油膜温度降低而减小，而斜盘材料的导热系数较小，热阻较大，导致斜盘的表面温度高于滑靴的表面温度，这是滑靴与斜盘受热膨胀不均匀的主要原因，因此影响滑靴副的热平衡间隙，严重时造成滑靴表面出现磨损迹象.

图5为热平衡间隙与柱塞腔压力之间的关系.热平衡间隙随缸体转角呈周期性变化，当滑靴处于柱塞腔的排油区时，滑靴所受的压紧力增大，热平衡间隙随挤压效应增强而减小，且热平衡间隙的最小值为3.1μm，出现在柱塞腔的吸排油过渡区，其原因是间隙油膜因压差和高速剪切作用所产生的功耗损失，转化为热量，引起油膜温度升高，加剧滑靴和斜盘的受热膨胀，减小热平衡间隙.当滑靴处于柱塞腔的吸油区时，间隙油膜所受的挤压承载效应减小，导致间隙油膜所产生的功率损失显著减小，引起油膜温度降低，减小滑靴和斜盘的膨胀变形，增大滑靴和斜盘之间的热平衡间隙.

图5 热平衡间隙与柱塞腔压力之间的关系Fig.5 Ther mal clearance versus cylinder pressure

3.1 不同柱塞腔压力的影响

图6为不同柱塞腔压力对热平衡间隙的影响.当柱塞腔压力从5 MPa上升到21 MPa时，热平衡间隙随柱塞腔压力增大而减小，且热平衡间隙的最小值从3.9μm降低到3.1μm，其原因是滑靴内腔油室压力是影响油膜控制体的焓值和功率损失的主要因素，表现为油液内能增加，与柱塞腔压力成正比，且与热平衡间隙的3次方成反比.在柱塞腔压力的作用下，热平衡间隙随挤压承载效应增大而减小，引起油膜温度升高，同时滑靴与斜盘的传热速率随油液温度升高而增大，加剧滑靴与斜盘的受热变形，减小热平衡间隙，这表明柱塞腔压力与油膜温度存在耦合效应，滑靴与斜盘的热变形对热平衡间隙产生一定的影响.

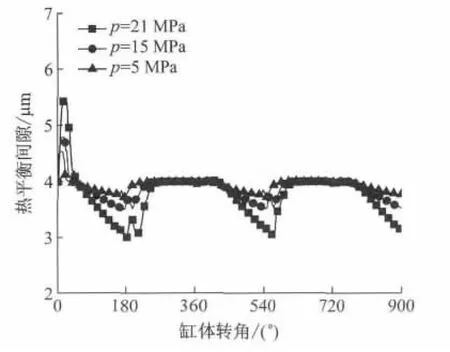
图6 不同柱塞腔压力对热平衡间隙的影响Fig.6 Effects of different cylinder pressure on thermal clearance

3.2 不同缸体转速的影响

图7为不同缸体转速对热平衡间隙的影响.当缸体转速从1000 r·min－1升高到2100 r·min－1时，滑靴副的热平衡间隙与缸体转速呈正相关，热平衡间隙的最小值从3.0μm升高到3.8μm，其原因是滑靴和斜盘的表面温升是影响热平衡间隙的主要因素，与传热速率以及油液温度相关.其中，间隙油液因剪切流所产生的黏性功率损失与缸体转速的平方成正比，而与热平衡间隙成反比，并将功率损失全部转化为热量，引起油液温度升高，造成滑靴和斜盘的受热变形，减小热平衡间隙.其次，滑靴在极薄的油膜厚度下运行时，滑靴底部油液因温度升高而发生膨胀，以至产生压力流动，而因转速升高所造成的热平衡间隙变厚，在某种程度上抑制了黏性摩擦功率损失，有利于增大热平衡间隙，避免滑靴表面发生黏着磨损.

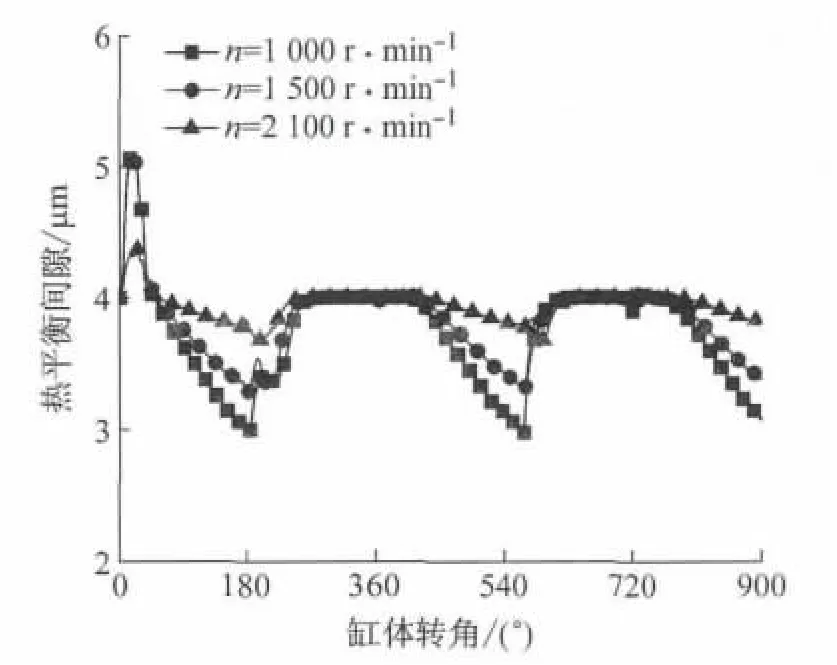
图7 不同缸体转速对热平衡间隙的影响Fig.7 Effects of different cylinder speed on thermal clearance

3.3 不同进口油液温度的影响

图8为不同进口油液温度对热平衡间隙的影响.滑靴副的热平衡间隙随进口油液温度升高而减小，当进口油液温度从35°C升高到50°C时，最小热平衡间隙从3.7μm降低到3.2μm，其原因是进口油液温度影响油膜控制体的热量积累和热传导，且油膜控制体的输入焓值与进口油液温度成正比，增加油液的内能，引起油膜温度升高，同时增强间隙油膜、滑靴和斜盘之间的对流换热，促使斜盘和滑靴因表面温度升高而产生膨胀变形，热平衡间隙减小，滑靴与斜盘之间的配合性能变差，造成滑靴运动不灵敏.因此，滑靴材料应当尽量选取线膨胀系数和热导率大的材料，对于斜盘则正好相反，有利于提高滑靴和斜盘之间的配合性能.

图8 不同进口油液温度对热平衡间隙的影响Fig.8 Effects of different inlet oil temperature on thermal clearance

4 理论结果与试验对比分析

4.1 不同工况下油膜厚度对比分析

由于轴向柱塞泵内部结构紧凑，所以在其内部安装测量装置比较困难，无法从滑靴底面测出连续变化的油膜动态特征.针对这一情况，设计了一种轴向柱塞泵滑靴副油膜厚度测量装置.采用双柱塞结构，缸体和柱塞组件（滑靴和柱塞）固定，通过电动机带动斜盘旋转来实现柱塞泵工作模拟，并利用负载泵为柱塞组件提供压力油[18].同时，在滑靴上加辅助支承环，将3个德国米铱公司所生产的耐压高达70 MPa，探头直径2.5 mm的EU型电涡流传感器成120°布置在辅助支承环上，将滑靴底面油膜波动引向辅助支承环，通过测量辅助支承环的轴向运动，从而推算出滑靴底部油膜厚度分布.本节选用文献[18]所给出的工作介质和滑靴的结构参数，对比研究不同压力、转速以及油液温度工况下油膜厚度的变化规律.

图9比较了不同压力和转速下油膜厚度的变化规律与文献[18]中试验结果.结果表明滑靴副油膜厚度随压力增大而减小，但随转速升高而增大，与文献[18]变化趋势较为一致，油膜厚度相差约1～2 μm，原因是文献[18]考虑了流体油膜动压效应的影响，对控制方程进行了修正，而本文采用静压支承原理建立数学模型.其次，文献[18]没有考虑滑靴表面变形的影响，而本文考虑了滑靴和斜盘因温度升高而产生的膨胀变形，在油膜厚度的计算公式中增加热变形项，计算方法优于前者.因此，在设计滑靴与斜盘的配合间隙尺寸时，需要考虑材料受热膨胀的影响，可利用滑靴副的热平衡间隙公式，选取适当的油膜厚度值进行校核，在热平衡间隙的基础上考虑一定的间隙余量.

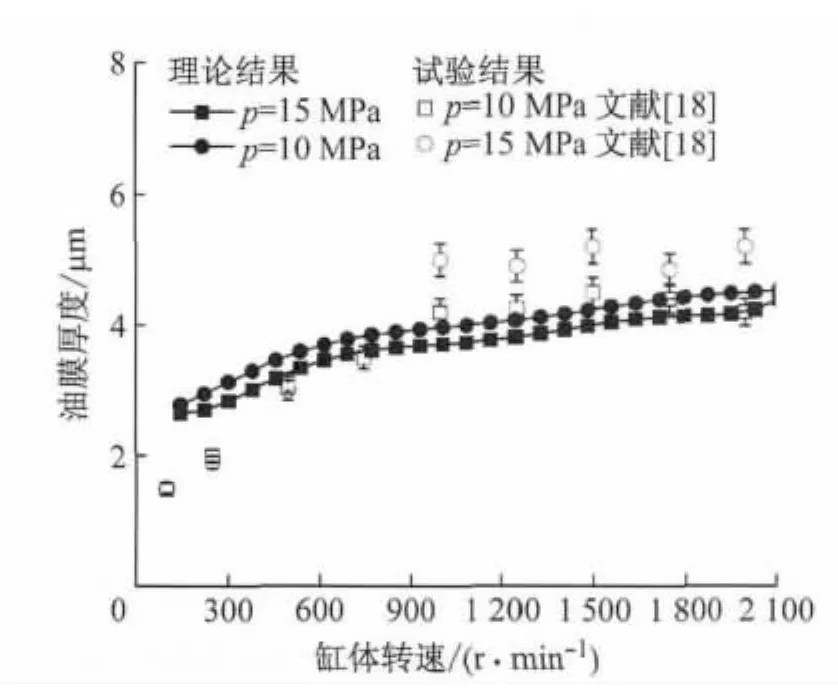
图9 不同转速和压力下油膜厚度Fig.9 Oil film thickness at different rotational speeds and pressures

图10为不同油液温度下油膜厚度的变化规律.由图10可知，不同压力等级下油液厚度随油液温度升高而减小，与文献[18]的理论和试验结果比较接近.当柱塞腔压力为15 MPa，且油液温度从43°C上升到80°C时，本文所计算的油膜厚度为3.7～4.4 μm，文献[18]所计算的油膜厚度为3.1～3.9μm，油膜厚度相差约为0.5μm，而文献[18]实际测试的油膜厚度为3.1～4.1μm，数值略有不同，其原因是文献[18]没有考虑油液黏度变化所带来的功率损失，而本文则基于能量守恒定律计算滑靴副因泄漏流量和黏性摩擦所产生的功率损失，并在油膜温度的计算公式中增加功率损失项，计算方法优于前者.这些特征说明油液黏度的变化会对滑靴副的能量损失造成影响，引起油膜温度升高，导致油膜厚度减小，加剧滑靴的黏着磨损.因此，本文采用滑靴副热平衡间隙公式，其计算结果符合实际工况下油膜厚度的变化规律，能够用来作为滑靴副间隙优化的设计方法.

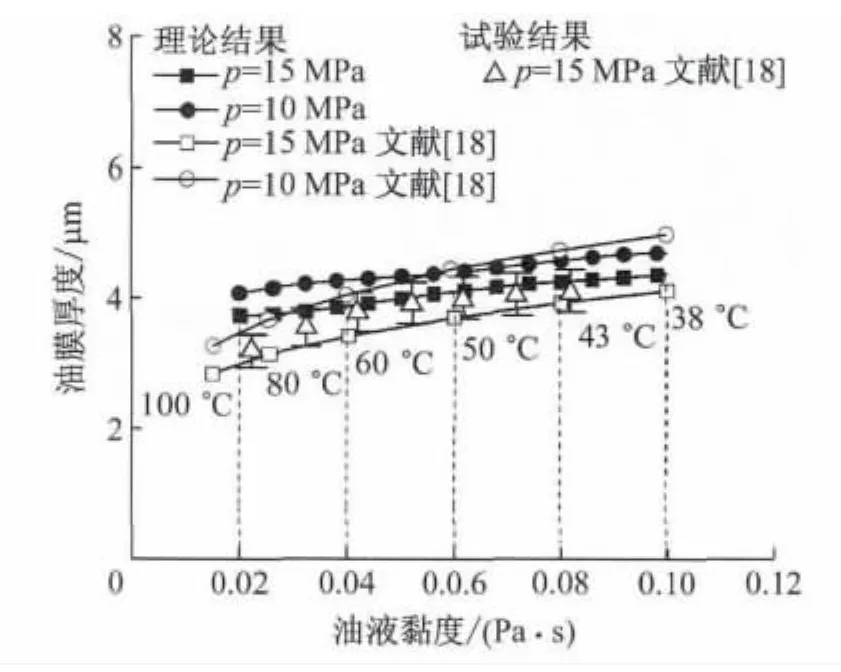
图10 不同油液温度下油膜厚度Fig.10 Oil film thickness at different oil temperatures

4.2 滑靴和斜盘的材料摩擦学试验

为了检验选配材料对滑靴和斜盘的摩擦学性能的影响，进行不同材料的摩擦磨损实验.在高速高压工况下，由于滑靴和斜盘之间相互接触而产生局部黏着磨损，所以滑靴和斜盘的配对材料应具有耐磨损性能.

4.2.1 试验材料选择

目前，滑靴采用铜合金类软材料，而斜盘则选择球铁材料，属于软／硬材料的配对方式.因此，滑靴选用ZY331608复杂黄铜、ZCuSn10Pb11Ni3铸造铜合金以及ZQSn10－2－3锡青铜，上述材料都具有良好的力学性能、耐热性和耐磨性.斜盘材料则选用QT500－7球墨铸铁，球墨铸铁具有较高的强度、塑性和韧性等优点，同时在高压工况下材料的耐磨性和减振性良好.为了验证材料配合的效果，需通过摩擦磨损实验进行论证.

4.2.2 试验方案

本次试验选用A4VTG90轴向柱塞泵作为测试对象，利用上述配对材料对滑靴和斜盘进行压力冲击环境下摩擦磨损试验.压力冲击试验条件为：环境温度为室温，进油口温度为40～60°C，进口压力为0.06～0.20 MPa，回油压力不大于0.18 MPa，转速为3500 r·min－1的工况下，额定压力为21 MPa，峰值压力为25 MPa，冲击频率为10次·min－1，冲击循环次数为10万次.通过压力冲击试验后，观察不同材料配对方案下滑靴表面的磨损程度，从而确定滑靴和斜盘材料的配对方案.

图11为试验前后滑靴表面的磨损情况.由于滑靴因离心力矩作用而产生倾覆，导致油膜的稳定性变差，局部区域发生金属接触，加剧了表面磨损.其次，使用精度为0.1 mg的分析天平测量试验前后滑靴的质量.表1为不同材料配对方案下滑靴的磨损量.滑靴的磨损量为0.013 9～0.056 3 g，其中，采用ZQSn10－2－3作为滑靴材料时，与 QT500－7进行摩擦学试验，试验后滑靴的磨损量最小，反映了滑靴材料具有良好的耐磨损性能，其原因是锡青铜的导热系数为153 W·（m·K）－1，而球墨铸铁的导热系数为80 W·（m·K）－1.因此，锡青铜具有优良的导热性能，虽然锡青铜的比热容（365 J·（kg·°C）－1）小于球墨铸铁（460 J·（kg·°C）－1），但是锡青铜的密度大于球墨铸铁，在同等体积的条件下铜温度升高1°C时所需吸收的热量与球墨铸铁相当，由于锡青铜的线膨胀系数（20.7×10－6°C－1）大于球墨铸铁（11×10－6°C－1），促使滑靴的表面形变大于斜盘，增大滑靴与斜盘之间的热平衡间隙，从而减少滑靴的磨损量.由此可见，采用ZQSn10－2－3与 QT500－7作为滑靴和斜盘的配对材料时，表现出良好的摩擦学效果.

图11 滑靴摩擦试验前后对比Fig.11 Com parison of slipper before and afterwearing test

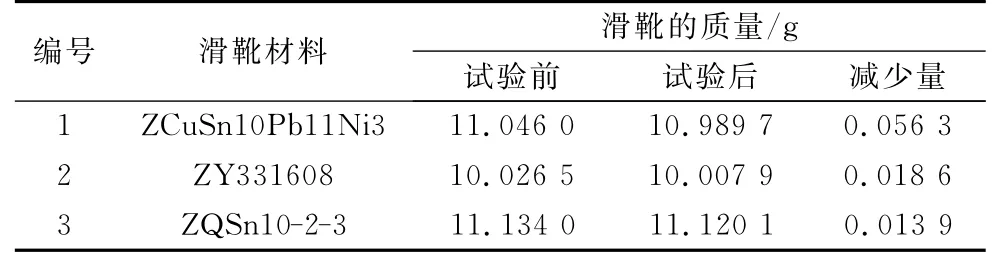
表1 不同滑靴材料的磨损量测试结果Tab.1 Wear test results of different slipper materials

5 结论

（1）文中提出了一种基于控制体能量守恒定律的滑靴副热平衡间隙公式.通过将间隙油膜、滑靴以及斜盘之间的热传递关系引入油膜厚度模型，获取滑靴副的热平衡间隙.

（2）滑靴底面间隙油液的功率损失与柱塞腔压力呈正相关，增大油液的内能，引起油液温度升高.柱塞腔压力与油液温度存在耦合效应，加剧滑靴与斜盘的受热变形，可减小热平衡间隙.缸体转速的提高促使油膜的黏性剪切作用增大，引起油膜温度升高，同时油液因温度升高而发生膨胀，产生压力流动，在某种程度上抑制了黏性摩擦功率损失，有利于增大热平衡间隙，减少滑靴表面磨损.

（3）轴向柱塞泵的进口油液温度影响油膜控制体的热量积累和热传导.油膜控制体的输入焓值与进口油液温度成正比，增加油液内能，使油膜温度升高，这是引起材料受热膨胀的主要原因.滑靴材料应当选取线膨胀系数和热导率大的材料，对于斜盘则正好相反，可增大热平衡间隙，提高滑靴与斜盘之间的配合性能，避免滑靴表面出现磨损现象.

[1] Khonsari M M，Radajivuc D J.Heat transfer in a thin－film flow in the presence of squeeze and shear thinning：application to piston rings[J].Journal of Heat Transfer，1997，119（2）：245.

[2] NIE Songlin， HUANG Guohua，ZHU Yuquan，et al.Sewhapm：development of a water hydraulic axial piston motor for underwater tool systems[J].Proceedings of the Institution of Mechanical Engineers，Part C：Journal of Mechanical Engineering Science，2005，219（7）：639.

[3] Prehn R，Haupert F，Friedrich K.Sliding wear performance of polymer composites under abrasive and water lubricated conditions for pump applications[J].Wear，2005，259（1－6）：693.

[4] Wieczorek U，Ivantysynova，M.Computer aided optimization of bearing and sealing gaps in hydrostatic machines－the simulation tool CASPAR [J].International Journal of Fluid Power，2002，3（1）：7.

[5] Koc E，Hooke C J.Investigation into the effects of orifice size，of fset and overclamp ratio on the lubrication of slipper bearings[J].Tribology International，1996，29（4）：299.

[6] Johnson R，Manring N D.Translating circular thrust bearings[J].Journal of Fluid Mechanics，2005，530（4）：197.

[7] Kazama T.Thermohydrodynamic lubrication model applicable to a slipper of swash plate type axial piston pumps and motors（effects of operating conditions）[J].Tribology Online，2010，5（5）：250.

[8] Bergada J M.Leakage and groove pressure of an axial piston pump slipper with multiple lands[J].Tribology Transactions，2008，51（4）：469.

[9] Kumar S，Bergada J M，Watton J.Axial piston pump grooved slipper analysis by CFD simulation of three－dimensional NVS equation in cylindrical coordinates[J].Computers ＆Fluids，2009，38（6）：648.

[10] LI Chenggong，JIAO Zhongxia.Thermal－hydraulic modeling and simulation of piston pump [J].Chinese Journal of Aeronautics，2006，19（4）：354.

[11] 潘景异，闻德生.CY型泵自冷却分析[J].燕山大学学报，2001，25（2）：110.PAN Jingyi，WEN Desheng.Analysis for self－coopling of CY bump[J].Journal of Yan Shan University，2001，25（2）：110.

[12] 孙毅，姜继海，刘成强.剩余压紧力条件下滑靴副的油膜特性及功耗[J].华南理工大学学报：自然科学版，2011，39（1）：111.SUN Yi， JIANG Jihai， LIU Chengqiang. Oil film characteristics and power consumption of slipper pair under redundant pressing force [J].Journal of South China University of Technology：Natural Science，2011，39（1）：111.

[13] XU Bing，ZHANG Junhui，YANG Huayong.Investigation on structural optimization of anti－overturning slipper of axial piston pump[J].Science China Technological Sciences，2012，55（11）：1.

[14] 汤何胜，訚耀保，李晶.柱塞泵滑靴副间隙泄漏及摩擦转矩特性研究[J].华南理工大学学报：自然科学版，2014，42（7）：75.TANG Hesheng，YIN Yaobao，LI Jing.Clearance leakage and friction torque of slipper pair in axial piston pump[J].Journal of South China University of Technology：Natural Science，2014，42（7）：75.

[15] 李壮云.液压元件与系统[M].北京：机械工业出版社，2011.LI Zhuangyun.Hydraulic compoments and system [M].Beijing：China Machine Press，2011.

[16] Sidders J A，Tilley D G，Chappie P J.Thermal－hydraulic performance prediction in fluid power systems[J].Proceedings of the Institution of Mechanical Engineers，Part I：Journal of Systems and Control Engineering，1996，210（14）：231.

[17] 闻德生.液压元件的创新与发展[M].北京：航空工业出版社，2009.WEN Desheng.Innoration and development of hydraulic[M].Beijing：Aviation Industry Press，2009.

[18] LIN Shuo，HU Jibin.Research on the Tribo－dynamic model of slipper bearings[J].Applied Mathematical Modelling，2015，39（2）：548.