钢筋混凝土筒仓-散料的静力相互作用分析

周长东，郭坤鹏，孟令凯，张晓阳

（北京交通大学 土木建筑工程学院，北京100044）

筒仓作为特种结构，广泛应用于储藏各类颗粒材料.筒仓与颗粒散料之间的静力相互作用十分复杂；同时，确定筒仓与散料之间的静力相互作用既是筒仓荷载与内力设计的前提，又是研究在地震作用下筒仓与散料颗粒相互作用的基础.关于散料颗粒对仓壁的压力计算，我国钢筋混凝土筒仓设计规范[1]与欧洲[2]（ISO）和美国[3]规范存在很大的不同；而且各国规范对于仓壁压力的计算都有不足[4].对于浅仓而言，我国采用Rankine理论进行仓内散料对仓壁的压力设计[1]；而欧洲等规范则采用Janssen理论进行设计[2－3].对于深仓，尽管我国与欧洲等国都采用Janssen理论进行仓内散料对仓壁的压力设计，但在设计时，各国规范所采用的侧压比系数计算方法却有很大不同[1－3].因此，为了研究各国规范筒仓仓壁静压力设计值是否具有足够的安全储备，有必要对仓壁与散料之间的静态压力作用进行研究.

目前，应用于模拟仓壁与散料之间相互作用的数值方法主要有有限元法（FEM）和离散元法（DEM）两种.有限元法发展较为成熟，其计算结果与精度为广大工程师所接受；离散元法作为一种相对较新的数值方法，基于对单个颗粒体力学行为进行研究，也可应用于模拟仓壁与散料散粒体之间的相互作用[5].但 Holst等[6－7]认为，离散元法对于模拟仓壁与散料散粒体之间相互作用有很大的离散性，有限元法则能收获较好的精度.因此，本文采用有限元方法对仓壁与散料散粒体之间静力相互作用进行数值模拟.

在采用有限元方法分析筒仓与散料之间的静力相互作用时，国内外多数学者[8－9]都假定散粒体为各向同性，并利用Drucker－Prager理论中黏性系数、内摩擦角和膨胀角三个参数来考虑散料的塑性变形阶段.然而，散料作为散粒体的集合，其应力状态往往在未达到Drucker－Prager理论中定义的屈服应力之前就出现散料内部散粒体重排列的现象[10]；同时，Drucker－Prager理论未能考虑散料初始孔隙比、颗粒硬度及颗粒间应变相对滑移幅值对仓壁压力分布的影响.因此，本文基于考虑散料初始孔隙比、颗粒硬度及颗粒间应变的亚塑性模型理论，利用大型通用有限元软件ABAQUS对钢筋混凝土筒仓仓壁与散料散粒体之间的静态压力作用进行三维有限元模拟，并将模拟结果与我国规范（GB 50077－2003）[1]、欧洲规范（EN 1991－4）[2]、美国筒仓设计规范（ACI 313－97）[3]以及既有试验数据[4]和经典筒仓压力理论进行比较.同时，文中还对仓内颗粒材料内摩擦角、摩擦系数、初始孔隙比、颗粒硬度及颗粒间应变进行参数分析，研究其对筒仓仓壁与散料散粒体之间的静态压力作用的影响.

1 数值模型

1.1 亚塑性本构理论

亚塑性本构理论以连续介质力学张量函数为工具，直接建立了应力率与应变率之间的关系，能够更好地描述颗粒材料初始塑性变形及完全发展的塑性变形，是一种较新的本构方程表征方法.

目前较为常见的亚塑性本构理论有 Wu－Bauer亚塑性模型、Gudehus－Bauer亚塑性模型、von Wolffersdorff考虑临界状态面的亚塑性本构模型[11]以及由Niemunis和Herle基于Von Wolffersdorff修正的亚塑性本构模型[12]等.

本文所采用的是由Niemunis和Herle基于von Wolffersdorff修正的亚塑性本构模型[12].该本构模型在保留von Wolffersdorff本构模型[11]能够较好模拟颗粒材料力学行为的基础上，解决了其在小应力循环下散粒体材料变形过度积累的棘轮效应问题.下面分别介绍von Wolffersdorff亚塑性本构模型[11]和 由 Niemunis和 Herle基 于 von Wolffersdorff修正的亚塑性本构模型[12].

1.1.1 von Wolffersdorff亚塑性本构模型

von Wolffersdorff亚塑性本构模型[11]的表达式为

标量因子a与临界状态极限面形状有关；φc为材料内摩擦角.

向密性函数fb的具体表达式为

式中：hs为颗粒硬度；n为按比例压缩能量法则时所对应的指数项；ei为在等向压缩时，颗粒材料在最小密度时对应的上限孔隙比；ei0为零压状态下颗粒材料可能达到的最大孔隙比；ec0为颗粒材料最大孔隙比；ed0为颗粒材料最小孔隙比.

正压性函数fe和fd的具体表达式为

式中：ec为散粒体材料临界孔隙比；ed为在等向压缩时，颗粒材料在最大密度时对应的下限孔隙比；α和β为确定三轴试验中内摩擦角峰值时所需要的指数项.

上述向密性函数fb，正压性函数fe和fd均考虑了颗粒材料密度和平均应力.其3个特征孔隙比ei，ec，ed都随着平均应力的增加而减小，并满足下述表达式：

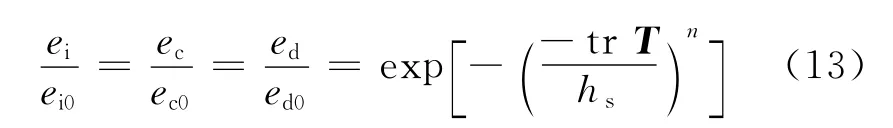
综上，von Wolffersdorff亚塑性本构模型需要8个材料参数：φc，ec0，ed0，ei0，hs，α，β和n.

1.1.2 Niemunis和Herle修正的亚塑性本构模型

Niemunis和Herle修正的亚塑性本构模型[12]表达式为

为了描述某一状态下颗粒间应变δ的状态，引入参数ρ，其表达式为：

式中：R为颗粒间最大应变；δ代表DΔt积累程度的二阶张量；‖‖为张量的欧几里得范数.

当ρ＝1时，

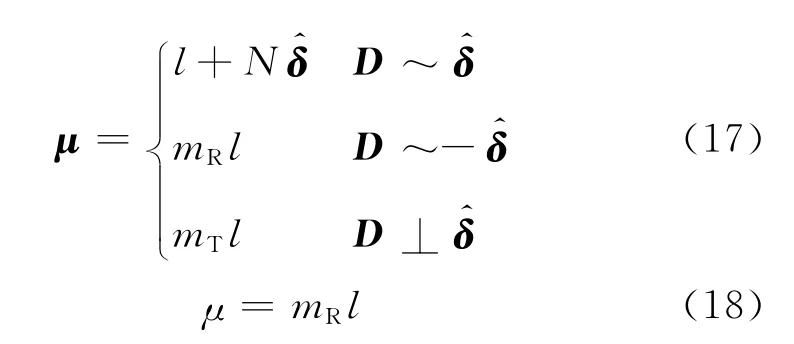
当0＞ρ＞1时，采用插值法确定颗粒材料刚度的一般表达式为

进而颗粒间应变的表达式为

综上，为了在Niemunis和Herle修正的亚塑性本构模型[12]中引入颗粒间的应变的概念，需要在上述von Wolffersdorff亚塑性本构模型[11]中8个材料参数基础上，补充5个材料参数：R，mR，mT，βr和χ.材料参数R为颗粒间应变上限值；mR和mT为在应变空间内，应变路径分别出现90°和180°负载时对应的刚度强化系数，其关系为mR＞mT＞1；材料参数βr和χ用来表示刚度变化的程度，ρβr为考虑当前颗粒间应变的加权系数.

1.2 数值模型方法及其合理性论证

本文采用ABAQUS中的UMAT子程序对钢筋混凝土仓壁－散料相互作用进行数值模拟，并将数值模拟结果与既有试验数据进行对比，从而验证本文数值模型的合理性和数值稳定性.

1.2.1 筒仓数值模型尺寸和材料本构关系模拟

在利用有限元软件ABAQUS对钢筋混凝土筒仓进行建模时，静力作用下仓顶对仓壁散料压力分布影响很小[13]，故忽略仓顶的影响.筒仓高26.0 m，内径28.0 m，壁厚0.3 m.散料顶点高度22.3 m，与仓壁相交高度21.3 m.利用ABAQUS中三维壳单元S4R模拟筒仓仓壁，利用三维实体单元C3D8模拟仓内散料.筒仓仓壁选用混凝土材料，其弹性模量E为3×1010Pa，泊松比μ为0.2，密度ρ为2 700 kg·m－3；筒仓内散料为小麦，其本构模型采用Niemunis和Herle修正的亚塑性本构模型[12]，其具体材料参数见表1和表2.

表1 定义亚塑性本构模型所需材料参数Tab.1 Material parameters of hypoplastic model

表2 基于颗粒间应变的附加材料参数Tab.2 Additional parameters of inter－granular strainconcept

1.2.2 筒仓壁－散料接触关系

本文利用有限元软件ABAQUS中主从接触面算法模拟筒仓壁与散料之间的接触关系.

筒仓壁与散料整体设定为刚柔接触；筒仓壁与散料表面采用面面接触；为了防止接触分析工程中从接触面侵入主接触面，本文对主从接触面之间的摩擦模型选用罚函数摩擦模型，并将摩擦系数按我国钢筋混凝土筒仓设计规范[1]取为0.4；由于本文重点是研究筒仓壁－散料静力相互作用，认为钢筋混凝土筒仓仓壁始终处于弹性状态，故本文中的数值模型不考虑几何非线性.

1.2.3 数值模型合理性验证

为了验证本文所采用的亚塑性本构理论及所建立数值模型边界条件的合理性，分别对筒仓实际结构和筒仓模型结构建立有限元数值模型，并将有限元数值模拟结果与陈长冰博士论文[15]中提供的筒仓实际结构试验数据进行对比分析，对比结果见图1.

图1 数值模拟结果与筒仓实际结构试验对比Fig.1 Com parison of numerical and practical results

由图1可知，采用本文所建立的有限元数值模型获得的结果与陈长冰[5]试验结果基本一致，从而验证了本文采用亚塑性本构理论模拟仓内散料的力学行为以及数值模型的合理性.

2 数值模拟结果与分析

2.1 数值模拟结果与各国规范比较

本文在进行筒仓仓内散料参数化分析时，为了更加直观地反映各个材料参数对仓壁所受侧向压力的影响，将仓内散料顶面处理为平面，高度为26.0 m，其余参数不变.

本文采用表1和表2的材料参数研究小麦对钢筋混凝土筒仓仓壁的侧向压力分布.在侧向压力分布上，杨鸿等[13]分析认为最大侧向压力分布在仓底；Juan等[14]指出底部压力为负值；杨代恒[15]分析认为最大侧压力分布在距离仓底一段距离处；我国[1]、欧洲（ISO）[2]、美国[3]筒仓设计规范则表明最大压力出现在底部.本文研究表明：最大侧向压力出现在筒仓仓底，这与文献[13]和各国规范结果保持一致，如图2所示.文献[14－15]之所以出现仓壁所受最大侧压力未分布在仓底的结果，是因为其对仓底散料节点进行位移全约束，这种约束形式与实际情况的边界条件不符.

图2 数值模拟结果与各国规范对比Fig.2 Com parison of numerical results and codes

同时，从图2可以看出，仓壁不同高度处各国规范值较数值模拟值（FEM）大8.7～23.5 kPa，这样的安全储备是各国规范综合考虑各类不确定因素的结果；其中最小储备值8.7 kPa约占仓底最大静压力值的11%左右.在筒仓静压力设计时，这样的安全储备是足够的.

2.2 数值模拟结果与经典筒仓理论比较

目前，比较经典的筒仓压力分布理论有Janssen理论、Rankine理论、修正的Coulomb理论、Airy理论等；现行的各国筒仓设计规范都以这些理论为基础进行筒仓压力设计.因此，本文将仓内散粒为小麦的数值模拟结果与这些经典的筒仓压力理论比较，对比结果见图3.

由图3可知，Janssen理论、Rankine理论及修正的Coulomb理论都将仓内散粒为小麦的数值模拟结果包络在内，这说明上述3种经典筒仓压力分布理论具有较高的安全储备；其中，利用Janssen理论所得到的筒仓压力分布值安全储备最高，这也是各国规范广泛采用Janssen理论的一个重要原因.

2.3 不同初始孔隙比对仓壁侧向压力影响

在对仓内散料进行材料参数化分析前，本文假定仓内散料初始孔隙比保持不变.之所以假定筒仓内散料初始孔隙比保持不变，是因为散料通过传送装置运至仓顶后自由落体至仓底或落入仓内既有散料的顶面，直至整个筒仓装料完毕；在整个装料过程中，大量散料颗粒碰撞，使得仓内散料在装料结束后密实程度很高，很难再进一步发生孔隙比的变化.

图3 数值模拟结果与经典筒仓压力理论对比Fig.3 Comparison of numerical results and classical theories

本文所提到的初始孔隙比指的是装料结束后，短时间内仓内散料所对应的空隙比。在随后的分析中，假定该初始孔隙比保持不变，进而讨论装料后不同情况下散料的初始孔隙比对仓壁静压力的影响。根据筒仓装料工作原理，文中假定初始孔隙比为常数，仓内散料的高度和密度不会随时间变化而变化.

基于初始孔隙比不变这一基本假定，本文在基于修正的von Wolffersdorff亚塑性本构模型进行散料－筒仓静力相互作用分析时，分别考虑颗粒材料初始孔隙比为0.40，0.45，0.50，0.55，0.60，0.65和0.70时对仓壁侧压的影响，分析结果见图4.

图4 初始孔隙比的影响Fig.4 Influence of initial void ratio

分析结果表明，颗粒材料初始孔隙比越大，其对筒仓仓壁的影响则越大.当散料初始孔隙比为0.40和0.45时，其对仓壁的压力分布较为接近；随着散料孔隙比的增加，其对筒壁侧压力值增幅明显.之所以出现仓内散料初始孔隙比越大，仓壁所受静压力越大，是因为散料初始孔隙比越大，其向仓壁周围的变形越大，筒仓仓壁对其的约束作用越强，仓壁所受静压力也越大.也就是说，同样的散料，在初始孔隙比不同的情况下，散料对仓壁的侧压力分布形式也有明显的差异.因此，在规范设计时，应当考虑仓内散料中初始孔隙比这个材料参数的影响.值得注意的是，颗粒材料并不是一直保持其初始孔隙比的大小；当颗粒材料在周围环境振动的作用下，其孔隙比会随着时间的变化而变化.图4同时也反映出仓内散料在堆积过程中受到环境扰动，孔隙比的改变对仓壁侧压力分布的影响.散料孔隙比在扰动下会有变小的趋势；正是由于这种趋势，散料对筒仓壁的压力也有减小的趋势.然而，多数文献在进行筒仓仓壁静力分析时，认为在重力作用下，仓内颗粒材料孔隙比基本保持不变.这样的假定忽略了散料对仓壁的侧压力是一个变化的过程，易高估筒仓仓壁承受散料对其侧向压力的能力.

2.4 散料与仓壁间摩擦系数对仓壁侧向压力影响

在实际工程中，散料与筒仓仓壁之间的摩擦系数一般集中在0.30～0.50范围内.本文在保持散料其他物理特性参数不变的情况下，取散料与仓壁间摩擦系数分别为0.30，0.35，0.40，0.45和0.50进行分析，结果见图5.

图5 摩擦系数的影响Fig.5 Influence of friction coefficient

从图5可以看出，仓壁在15～20 m高度范围内，对应的5条仓壁侧压力分布曲线基本重合；仓壁在0～5 m高度范围内，其对应的5条侧压力分布曲线有所差异，但相差约5 kPa.上述分析结果表明，不同摩擦系数对仓壁侧向压力影响很小.

2.5 散料内摩擦角对仓壁侧向压力的影响

实际工程中，仓内散料的内摩擦角一般在22°～40°范围内.本文在保持散料其他物理特性参数不变的情况下，分别对散料内摩擦角为22°，25°，28°，31°，34°，37°和40°进行分析，结果见图6.

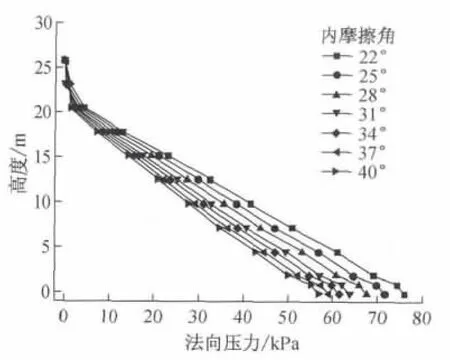
图6 散料内摩擦角的影响Fig.6 Influence of internal friction angle

从图6可以看出，仓内散料的内摩擦角对筒仓壁侧向压力分布影响很大.随着散料内摩擦角的增大，仓壁静压力在减小，这是因为仓内散料内摩擦角越大，散料颗粒间相互咬合力也越大，因此会减小散料颗粒对仓壁的法向变形，即仓壁对与其接触的散料约束作用变小，仓壁所受静压力也变小；同时，在距离仓底约0.5 m高度范围内，不同内摩擦角的散料对仓壁产生的侧向应力差异非常明显，最大时甚至相差20.3 kPa，其原因是仓内散料在重力作用下出现了较大的塑性变形.因此，进行筒仓仓壁内力设计时，应当充分考虑散料内摩擦角及塑性变形对筒仓壁静力作用的影响.

2.6 不同颗粒粒径的筒仓仓壁侧向压力分析

散料颗粒硬度是间接反映颗粒粒径大小的材料参数，其范围一般为1 000（细砂）～30 000 MPa（粗砂和砂砾）.本文在保持其他材料参数不变下，选取颗粒硬度分别为1 000，1 800，4 000，6 000，8 000，10 000和30 000 MPa进行分析，结果见图7.

图7 不同颗粒硬度的影响Fig.7 Influence of different granulate hardness

从图7可以看出，散料颗粒粒径越小，仓壁所受侧向压力越大；筒仓底部不同颗粒粒径所对应的最大与最小侧向压力相差约12 k Pa.这说明散料颗粒粒径的大小对筒仓仓壁所受侧向压力的影响较大.然而，在现行各国规范中，并未将散料的颗粒粒径考虑到筒仓仓壁侧向压力的设计之中.

3 结论

本文基于修正的von Wolffersdorff亚塑性本构理论对筒仓仓壁与散料颗粒材料之间的静态压力作用进行有限元模拟.可得出以下结论：

（1）将筒仓－散料静力相互作用的数值模拟结果与既有筒仓试验数据、中欧美筒仓设计规范及经典筒仓压力理论进行对比，结果表明采用亚塑性本构理论模拟散料能够较为准确地反映仓壁与散料相互作用的实际状况.

（2）通过对仓内散料初始孔隙比、内摩擦角、摩擦系数、颗粒硬度和颗粒间应变进行参数分析，认为散料受初始孔隙比、内摩擦角、颗粒硬度和颗粒间应变影响较大，建议规范按照材料参数分类进行筒仓仓壁静力压力设计.

（3）通过对反映粒径大小的颗粒硬度进行参数分析，分析结果表明颗粒粒径大小对筒仓仓壁压力影响较大，且颗粒粒径越大，仓壁所受压力越大；建议规范给出同类型散料颗粒粒径最大值，并借助有限元软件取最大粒径值进行筒仓静力压力设计.

[1] 中华人民共和国建设部.GB 50077－2003钢筋混凝土筒仓设计规范[S].北京：中国计划出版社，2004.China Ministry of Construction.GB 50077－2003 Code for design of reinforced concrete silos [S].Beijing：China Planning Press，2004.

[2] European Committee for Standardization.Eurocode 8 Design of structures for earthquake resistance，part 4：silos，tanks and pipelines [S]. Brussels： European Committee for Standardization，2006.

[3] American Concrete Institute（ACI）.Standard practice for design and construction of concrete silos and stacking tubes for storing granular materials[S].Detroit：American Concrete Institute，1997.

[4] Carson W.Limits of silo design codes[J].Practice Periodical on Structural Design and Construction，2014，10（10）：61.

[5] 陈长冰.筒仓内散体侧压力沿仓壁分布研究 [D].合肥：合肥工业大学，2006.CHEN Changbing.Research on distribution of lateral bulksolid pressures on silos’walls[D].Hefei：Hefei University of Technology，2006.

[6] Holst J，Ooi J，Rotter J，et al.Numerical modeling of silo filling.Ⅰ：continuum analyses[J].Journal of Engineering Mechanics，1999，125（1）：94.

[7] Holst J，Ooi J，Rotter J，et al.Numerical modeling of silo filling. Ⅱ：discrete element analyses [J].Journal of Engineering Mechanics，1999，125（1）：104.

[8] WAN Xuewen，YANG Zhaojian，SHU Xuefeng，et al.The static contact statuses between granular materials and flatbottomed steel silos[J].Powder Technology，2013，235：1053.

[9] Guaital M，Couto A，Ayuga F.Numerical simulation of wall pressure during discharge of granular material from cylindrical silos with eccentric hoppers [J].Biosystems Engineering，2003，85（1）：101.

[10] Herle I，Gudehus G.Determinations of parameters of a hypoplastic constitutive model from properties of grain assemblies[J].Mechanics of Cohesive Materials，1999，4：461.

[11] Von Wolffersdorf f. A hypoplastic relation for granular materials with a predefined limit state surface[J].Mechanics of Cohesive Materials，1996，1（3）：251.

[12] Niemunis A，Herle I.Hypoplastic model for cohesive soils with elastic strain range [J].Mechanics of Cohesive Materials，1997，2（4）：279.

[13] 杨鸿，杨代恒，赵阳.钢筒仓散料静态压力的三维有限元模拟[J].浙江大学学报：工学版，2011，45（8）：1423.YANG Hong， YANG Daiheng， ZHAO Yang. Threedimensional finite element simulation of static granular material pressure for steel silos[J].Journal of Zhejiang University：Engineering Science，2011，45（8）：1423.

[14] Juan A，Moran J M，Guerra M I，et al.Es
Tablishing stress state of cylindrical metal silos using finite element method：comparison with ENV 1993 [J].Thin Walled Structures，2006，44（11）：1192.

[15] 杨代恒.钢筒仓设计研究及散料压力的数值模拟 [D].杭州：浙江大学，2008.YANG Daiheng.Design research of steel silos and numerical simulation of bulk materials pressure[D].Hangzhou：Zhejiang University，2008.