相向/同向转子密炼机混合效率的数值模拟

刘金朋，李凡珠，杨海波，张立群

（北京化工大学 北京市新型高分子材料制备与加工重点实验室，北京 100029）

为了提高密炼机的混炼质量，缩短混炼时间，降低加工能耗，需要对密炼机的混炼过程和混炼机理进行深入研究，以便开发设计高混炼质量、高产量、低能耗的密炼机转子，并为密炼机的工业应用提供科学依据。随着计算机技术的发展，有限元数值模拟作为一种新兴的方法成为实际实验方法的有效补充。20世纪80年代，国外开始利用数值模拟方法对密炼机胶料流动进行研究，得到了一些有价值的结论[1-6]，目前国外对密炼机内胶料流动的研究已基本完善。近年来，国内对密炼机内胶料流动的分析也逐渐增多，并取得了一定的成果[7-10]。

本工作基于流体力学分析软件Fluent的UDF方法和动态网格技术分别对相向旋转和同向旋转转子密炼机混炼流场进行三维模拟，得到每一时刻流场的压力、速度、粘度、剪切应力和混合指数分布。通过对模拟结果进行后处理，比较相向和同向旋转转子密炼机的分散混合和分布混合性能。

1 流动模型的建立

针对本中心实验室的SHR-10DY型混合机的F系列四棱转子建立胶料混炼过程的几何物理模型和数学模型，运用动态网格技术，定义密炼机转子的转动，并使用有限体积法离散单元，建立胶料混炼流场的三维有限元模型。

1.1 物理模型

采用专业三维造型软件Pro/E对密炼机的转子和混合室进行三维建模，如图1所示。其中混合室内径为46 cm，轴长为76 cm，转子根径为30 cm，外径为42 cm，中心距为45 cm。

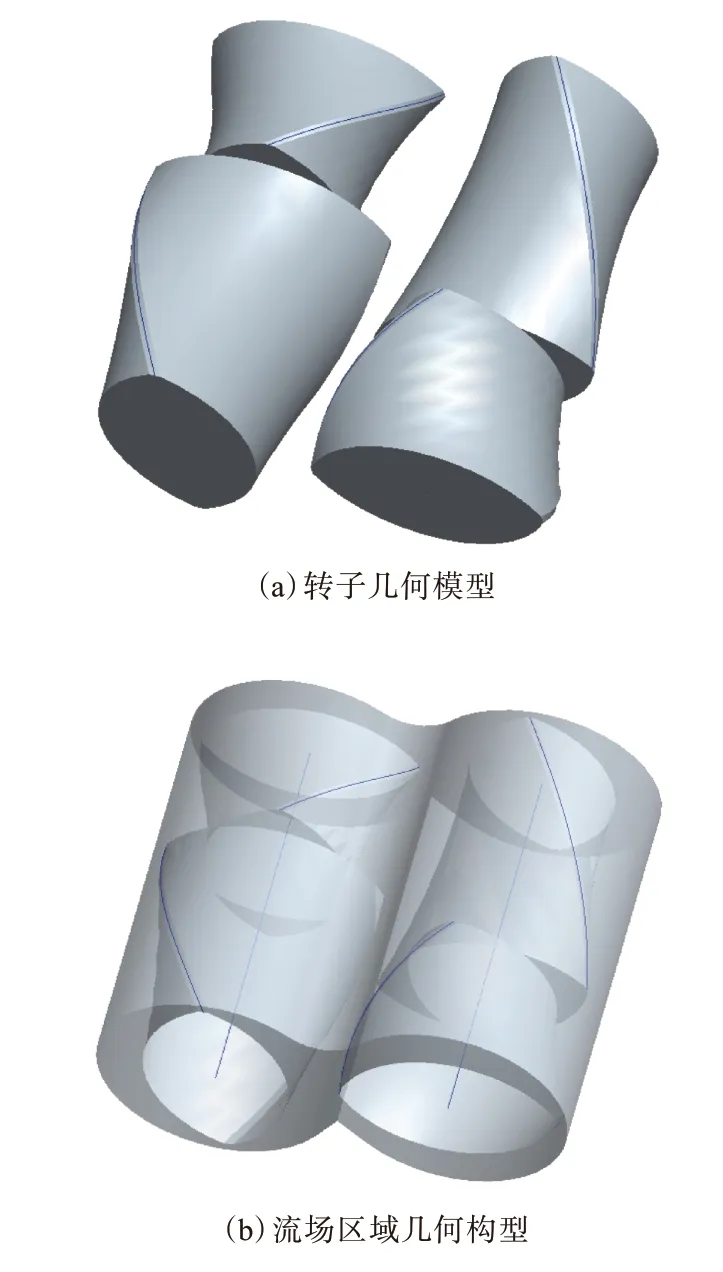
图1 密炼机转子和三维流场构型

1.2 数学模型

为便于模拟，同时能够满足工程的近似要求，对混炼流场做以下假设：流场为全充满等温流场；胶料为不可压缩非牛顿流体；胶料流动形式为层流且在壁面上无滑移。基于以上假设，描述流场的连续性方程和动量方程分别为

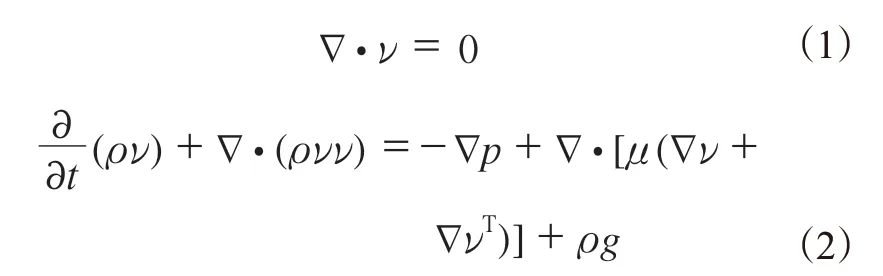
式中，t为混炼时间，ν为流体速度，p为压力，ρ为密度，μ为粘度，哈密尔顿算子∇为

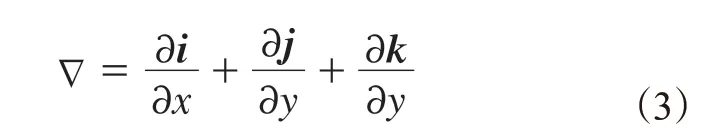
式中，i，j和k分别为x，y和z坐标轴上的单位矢量。

本文采用Bird-Carreau模型作为橡胶流体的本构方程，其表达式为

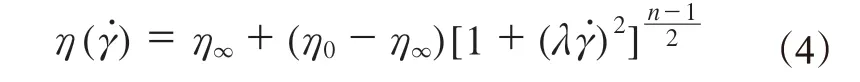
式中，η0为零剪切粘度，Pa·s；η∞为无穷剪切粘度，Pa·s；λ为粘弹性的特征时间，s；γ˙为剪切速率，s-1；n为幂律指数。

在温度为100 ℃时，测量丁苯橡胶混炼胶的物性参数如下：ρ为1 100 kg·m-3；η0为0.22×105Pa·s；η∞为0.82×10-5Pa·s；λ为0.12；n为0.086。

1.3 有限元模型

图2所示为转子三维流场的有限元网格模型，笛卡尔坐标系原点设在密炼室后壁面的中心位置。本工作通过GAMBIT对三维流场进行网格划分并指定边界类型，考虑到计算区域的复杂性，采用四面体网格划分，该有限元模型包括475 596个单元、92 797个节点和5个边界。

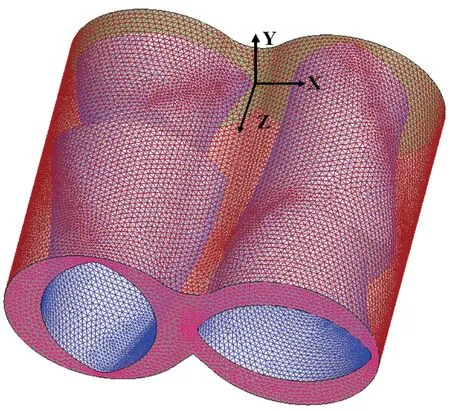
图2 转子三维流场的有限元网格

1.4 边界条件

Fluent动态网格技术用于处理计算域由于边界运动而发生变化的非稳态问题，网格的更新由Fluent根据每个迭代步中边界的变化情况自动完成。这种方法实现了转子真正意义上的转动，通过转子表面产生的节点速度来拖拽液体边界中节点的运动，从而产生具有正确方向和大小的速度条件。在使用动态网格模型时，首先定义初始网格分布、边界运动方式并指定参与运动的区域。本工作边界条件设定为：所有固体壁面为无滑移边界，通过外加UDF控制左右两转子旋转，转速为60 r·min-1。

2 模拟结果与讨论

为方便观察与描述，定义3个轴向截面如图3所示，其中Z1=0.10 m，Z2=0.38 m，Z3=0.66 m。

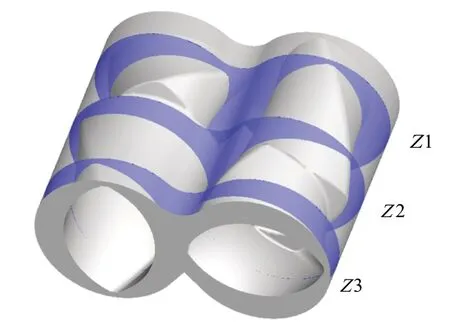
图3 定义截面示意

2.1 剪切速率场

图4为t=10 s时3个轴向截面的剪切速率分布。可以看出：转子棱顶处的剪切速率最大；其他宽间隙区域的剪切速率维持在中下等水平，其等值线围绕着转子呈近似的层状分布；从密炼室壁开始，越靠近转子根部剪切速率越小，贴近转子根部的一层胶料的剪切速率几乎为零，说明这一层胶料只是转子转动而不发生剪切变形。

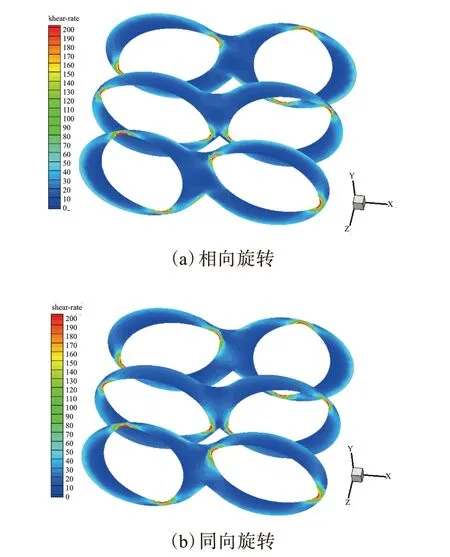
图4 Z1，Z2和Z3截面的剪切速率分布（t=10 s）

从数值上看，与转子棱顶处相比，宽间隙区域剪切速率相差较大，剪切速率基本为40 s-1以下，而转子棱顶处剪切速率基本都在100 s-1以上，最高处可达7 000 s-1。因此该剪切型密炼机在转子棱顶处具有优异的分散混合性能，但局部的高剪切作用会使胶料温度局部升高导致胶料焦烧，这也是剪切型转子的不足之处。

2.2 粘度场

粘度是剪切速率的函数，粘度场可以反映物料在流场的不同区域内受剪切的程度。由Bird-Carreau本构方程可知，剪切速率越高，粘度越低。为对比相向旋转和同向旋转流场的粘度场，对所有网格的粘度值进行体积积分，可以得到整个流场粘度的体积加权平均值：

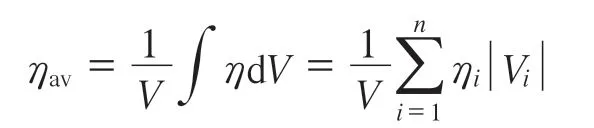
式中，ηav为体积加权平均粘度，Pa·s；V为流场体积，m3；η为橡胶粘度，Pa·s；ηi为第i个单元的橡胶粘度，Pa·s；Vi为第i个单元的体积，m3；n为单元数目。

图5所示为一个周期内两种工艺条件下平均表观粘度随流动时间的变化曲线。由于不同时刻两转子的相位关系不同，胶料受到的剪切、挤压、拉伸作用不同，致使平均表观粘度因时间而异。由图5可见：转子相向旋转时，粘度波动范围较大，说明转子间的相位关系对流场剪切速率影响较大；转子同向旋转时，粘度在较小的范围内波动，具有时间上的稳定性。除此之外，同向旋转时的流场平均表观粘度总是小于相向旋转时的平均表观粘度，说明转子同向旋转能够提供较大的剪切速率，对胶料实施更有效地剪切。

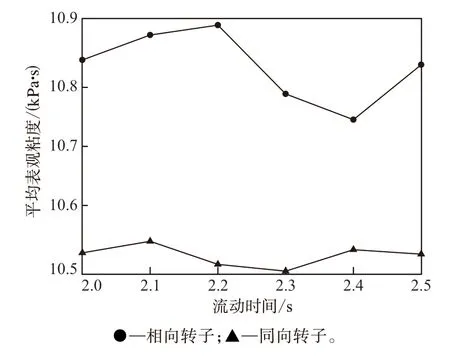
图5 平均表观粘度随流动时间的变化曲线

2.3 剪切应力

混炼过程中，决定混炼速度的关键是分散，主要取决于混炼过程的剪切应力，强烈的剪切作用产生的巨大剪切力可以打破橡胶与炭黑的聚集体，达到初步分散的效果。如果剪切应力太小，则难以达到良好的分散效果。图6所示为一个周期内两种工艺条件下平均剪切应力随时间的变化曲线。可以看出，同向旋转的平均剪切应力总是大于相向旋转时的平均剪切应力，说明转子同向旋转能够保持较大的剪切应力，达到较好的初步分散效果。

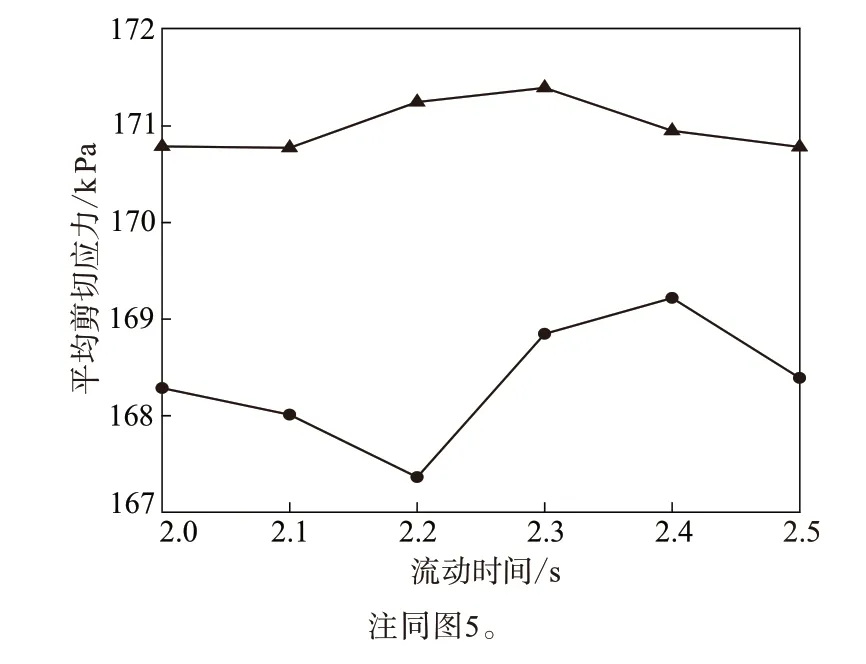
图6 平均剪切应力随流动时间的变化曲线

2.4 分散混合

本工作采用混合指数λMZ表征两种工艺条件下密炼机的分散混合性能。混合指数λMZ由I.Manas-Zloczower等[11]提出，表达式为

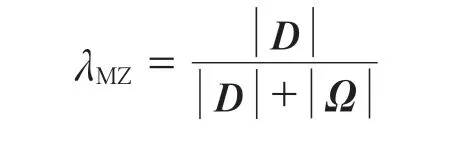
式中，|D|为形变速率张量的模，|Ω|为旋转速率张量的模。对于纯固体旋转，没有形变发生，混合指数λMZ为零。对于简单剪切流动，形变速率张量和旋转速率张量的模相等，混合指数λMZ为0.5。对于拉伸流动，没有旋转发生，其混合指数λMZ为1。由于混合指数可代表熔体流动类型，因此可以间接表征密炼机的分散混合程度。

图7所示为t=10 s时3个轴向截面的混合指数分布。从图7可以看出，旋转流动主要分布于转子棱根处。转子与密炼室壁之间的宽间隙区域为从小到大再从大到小的过程，当物料受到挤压时被迫运动到空隙较大的地方，这个挤压流动的过程也是拉伸流动的过程，聚合物伴随该过程经历了一次拉伸变形，使得物料在转子中间被反复拉伸和挤压，对于分散相的分散混合操作尤为有利。纯剪切流动（λMZ＝0.5）主要分布于转子棱顶间隙，流场其他区域的混合指数为0.4～0.6，流体流动特点主要为剪切流动。由图7（a）和（b）对比可知，相向旋转时，两转子之间的流场存在大片混合指数接近于1的区域，说明此区域存在较多的拉伸流动；同向旋转时，此处的流场明显为剪切流动场。

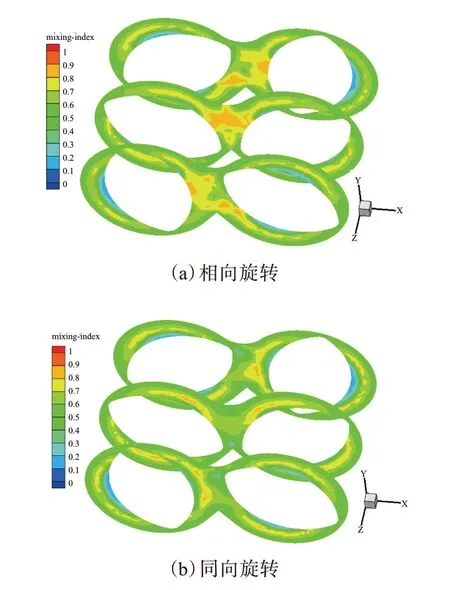
图7 Z1，Z2和Z3截面上的混合指数分布（t=10 s）

图8所示为两种流场的体积加权平均混合指数随时间变化的对比曲线。相向旋转时转子间的相位关系对流体流动特征影响较大。与同向旋转相比，转子相向旋转的平均混合指数较大，说明转子相向旋转能够对胶料实施有效的剪切和拉伸，使炭黑等填料破碎分散并阻止聚集。

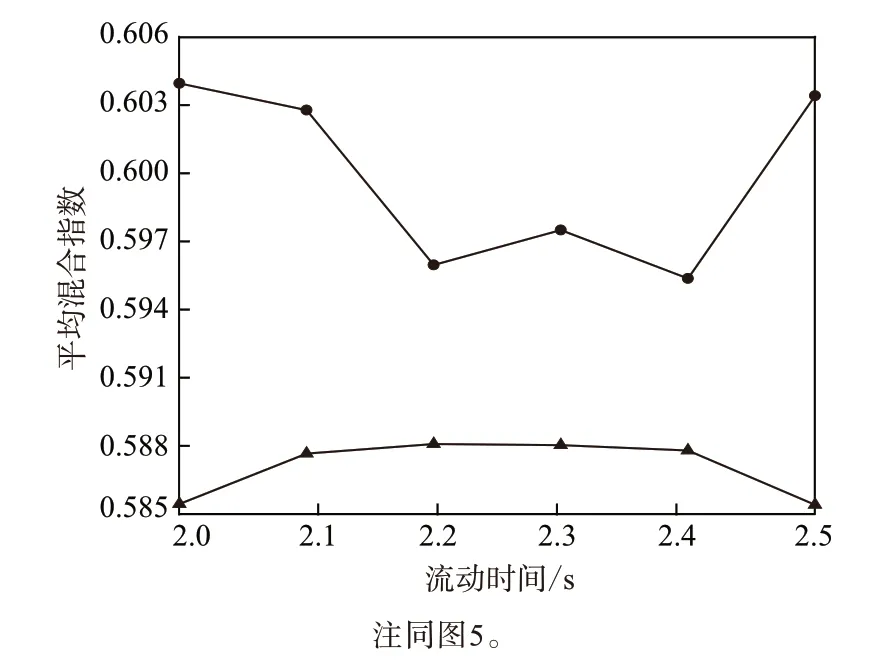
图8 平均混合指数随流动时间的变化曲线

图9所示为相向转子和同向转子在6个时刻的流场混合指数对比。由图9可以看出，两种情况下，混合指数为0.4～0.6的区域均占整个混合流场总体积的约70%，即两种混炼流场主要是以剪切为主，纯旋转流场和纯拉伸流场只占很小的部分。与相向旋转相比，同向旋转时的流场包含更多的剪切流动，因此平均剪切速率比相向旋转时大，平均粘度比相向旋转时小；而相向旋转时包含较多的拉伸流场，较多拉伸流场的存在对于分散混合非常有利。

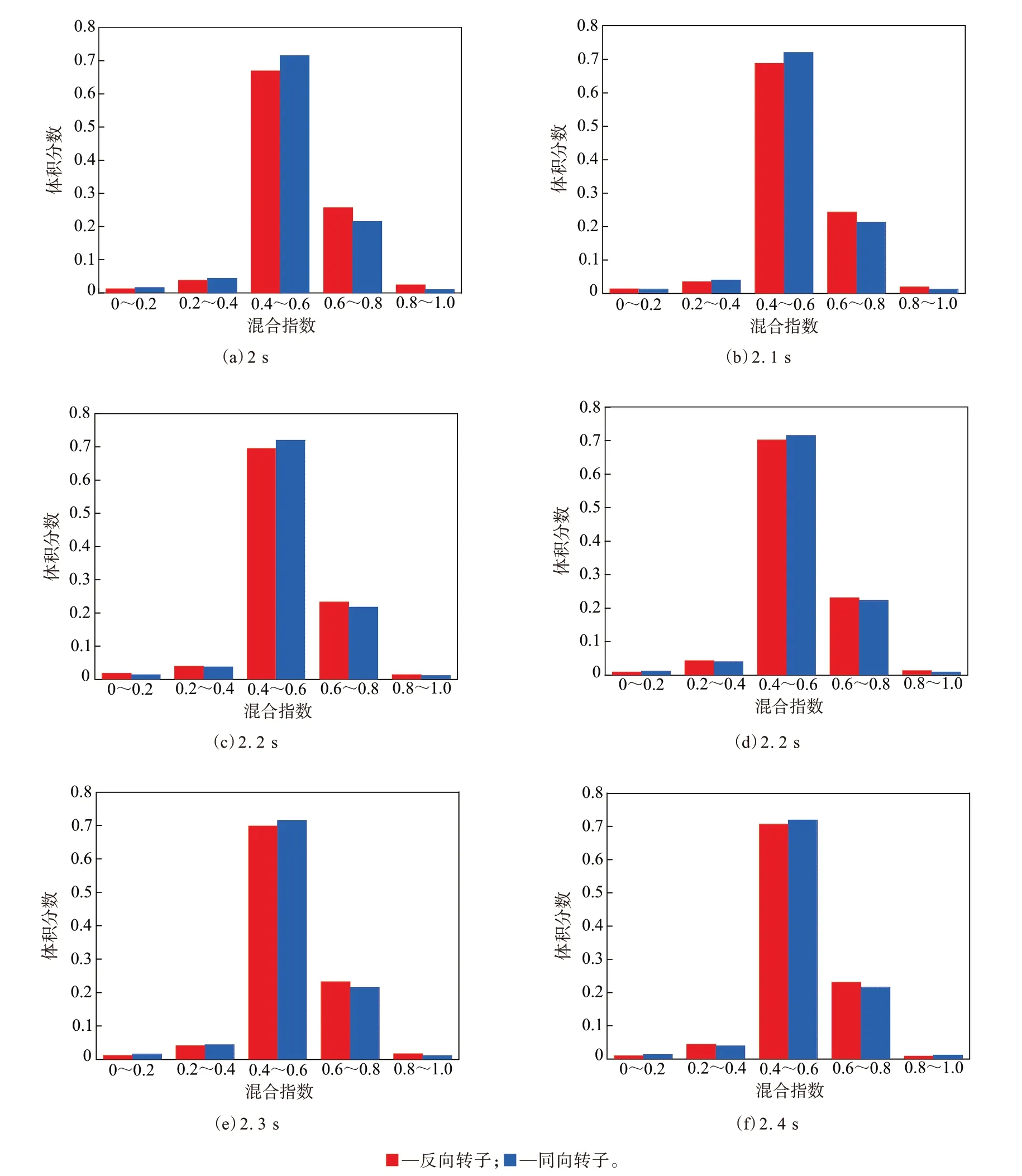
图9 不同时刻流场混合指数对比直方图

2.5 分散混合

对于瞬态模拟，加入离散相进行粒子追踪，可以得到某一时刻粒子分布情况，也可以对粒子运动轨迹进行分析。本工作利用可视化粒子追踪考察密炼过程中分散相在胶料中的分布情况，图10所示为离散相粒子初始释放位置，跟踪粒子初始时刻从3条线上释放。跟踪粒子作为离散相，计算基于如下假设：粒子所占体积分数很小，忽略颗粒相对连续相的影响，计算采用非耦合方式进行；忽略颗粒间的相互作用；颗粒与壁面的碰撞为完全弹性碰撞；示踪粒子为碳颗粒，密度为2 kg·m-3，直径为1 μm。

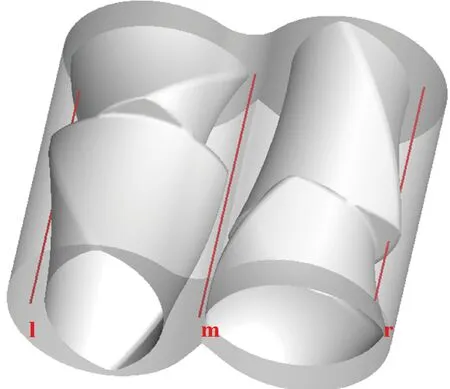
图10 粒子释放位置示意

为对比两种工艺条件下的轴向混合能力，定义轴向位移尺度δi为

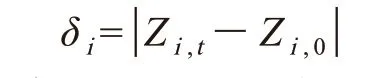
式中，Zi,0和Zi,t分别为粒子i在初始和t时刻的Z轴坐标。对N个追踪粒子可求得任意时刻的平均值，其平均值越大，表示轴向分布越好。每隔0.2 s对两种工艺条件下的粒子所在空间坐标进行统计，可以得到两种工艺条件下粒子的平均轴向位移尺度随时间变化曲线，如图11所示。由图11可见，两种工艺条件的平均轴向位移尺度基本随时间的延长而逐渐增大，在前20 s时间内，转子同向旋转密炼机的轴向位移大于相向旋转密炼机，20 s以后两者到达相同的平台。从数值上看，两者的平均值非常小，说明两种转向密炼机的轴向分布能力较差，除转子结构外，全充满这一假设因素也可能对胶料轴向移动产生影响。

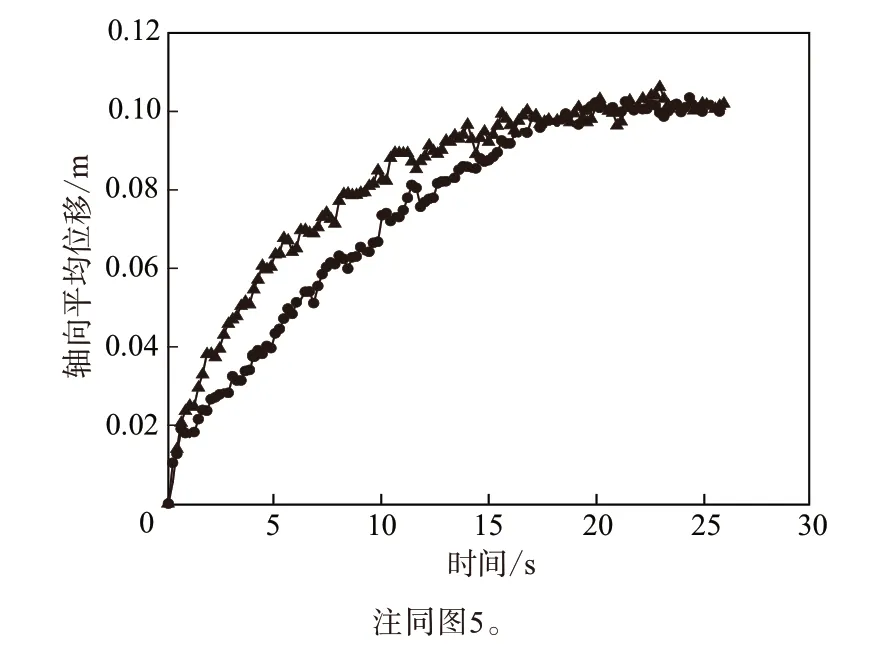
图11 轴向平均位移随时间变化曲线

引用材料拉伸参数l[11]对混合分布效率进行定量分析，拉伸参数l定义如下：

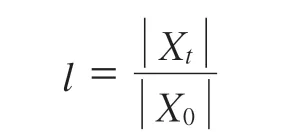
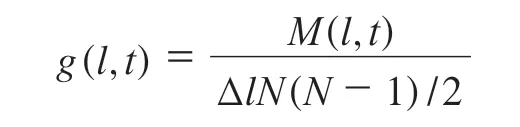
式中，M（l,t）为t时刻时拉伸长度处于（l－Δl/2）到（l＋Δl/2）之间的粒子对总数。利用拉伸长度分布g(l,t)，可利用下式求得任意时刻的拉伸长度平均值越大，代表分布效率越高。

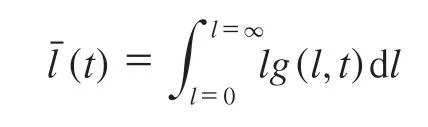
每隔0.2 s对离散相粒子所在空间位置进行统计，并求得相应的平均拉伸长度，由此可以得到两种工艺条件下粒子的平均拉伸长度随时间变化的曲线，如图12所示。起初粒子均排布在一条直线上，平均拉伸长度小，随着转子的转动，粒子逐渐分散开来，相互之间距离增大，则平均拉伸长度也相应增大。从数值上看，两种情况的平均拉伸长度相差较多，随着混炼时间继续延长，两种情况的平均拉伸长度相互接近且进入平台区，说明两种情况粒子都达到了较好的分布。

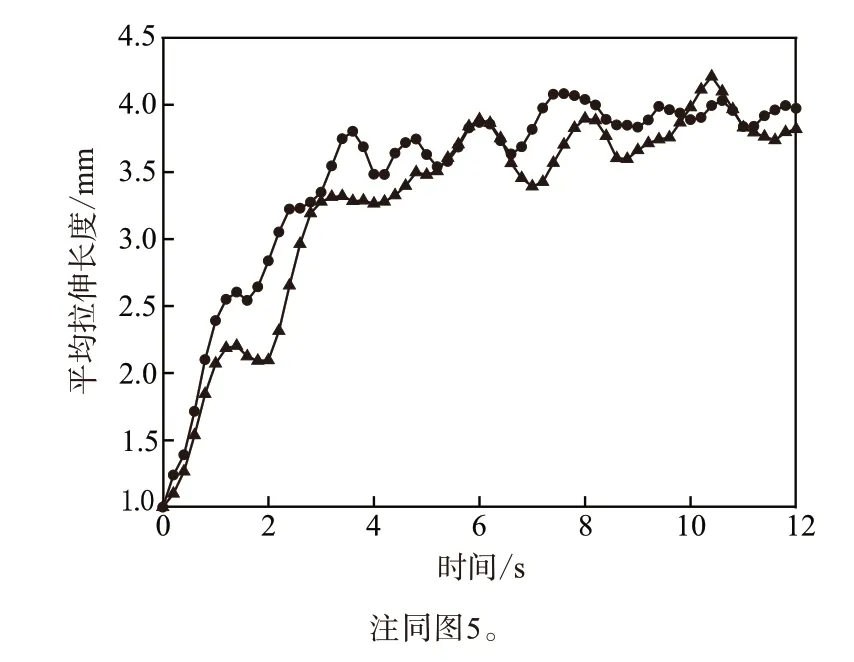
图12 平均拉伸长度随时间的变化曲线

3 结论

本工作对相向和同向转子密炼机混炼流场分别进行了数值模拟和离散相追踪，并运用统计学的观点，采用混合指数、轴向位移尺度和拉伸参数对相向和同向转子密炼机的分散混合和分布混合性能进行了对比研究，得出如下结论。

（1）与相向转子相比，同向转子密炼机存在较多的剪切流场，能够提供较高的平均剪切速率和平均剪切应力；而相向转子密炼机则包含较多的拉伸流场，分散混合性能较好。

（2）混炼前期，两者的分布混合性能有所差异，后期两者的轴向位移尺度和拉伸参数均到达相同的平台区，两者的混合分布能力相近。