农村高中数学课堂一题多解的误区
文/黄进标
课堂上进行“一题多解”的教学,不但可以训练学生的发散思维,还可以培养学生思维的灵活性和创造性。因此有些教师认为课堂教学解法越多越好,却往往没有反思一下,在高中阶段普及化的大环境下,农村高中学校学生的入学成绩参差不齐,总体水平偏中下,这种情况下课堂上过多的解法介绍有必要吗?大多数学生能理解掌握吗?所以农村高中数学课堂“一题多解”的教学应注意以下三点误区:
误区一:过多关注个体,忽视全体,课堂成为部分学生的辅导课
农村高中学生在重点校的层层筛选下,大部分学生原有知识水平结构不全面,学习方法欠缺,理解力不强。
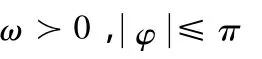
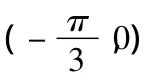
解法一利用最高点或最低点的方法应该重点讲解,要讲透,板书详细规范,让大部分学生能够理解掌握。解法二看起来很简便,但学生不易理解,只能靠死记下来。
误区二:追求多解却增加了学生的学习负担
课堂教学时为了体现多角度解题的思想方法,在已有知识不能解决的情况下,不得不补充些教学大纲不做要求的知识内容,无形中增加了学生的学习负担,进一步加深学生害怕学数学的心理因素。
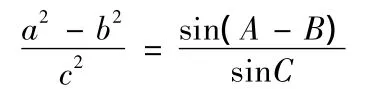
分析过程:三角恒等式证明常有三种思路:证左边=右边、证右边=左边、两边凑。
证法一:证右边=左边
证法二:证左边=右边
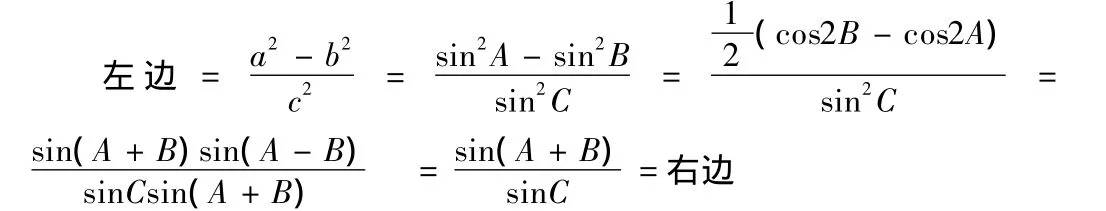
本题的证明主要是利用正余弦定理,进行边与角的互化,证法一是角化边,所用知识学生理解并能掌握,若教师为了体现思路的多角度,不考虑学生的学情,在证法二上花了大量的时间精力补充和差化积公式的有关知识,学生听得费力又消化不了。课堂成了教师的独角戏,学生无法参与教学之中,更谈不上能多角度思考问题。
误区三:眼高手低过于注重解题技巧
通性通法的解题方法能有效地检测学生对学数学知识中所蕴含的数学思想和方法掌握程度。要是课堂上过于注重解题技巧,人为地制造数学的神秘感,使学生觉得数学深不可测、捉摸不透,这样学生会慢慢的对数学失去兴趣。课堂上再多、再好的解法,最终还是竹篮打水一场空,教学效果是很低的。
解法一:利用等差数列的五个基本量a1,d,n,sn,an,根据等差数列的前n项和公式列出方程组,求出a1和d,即可求出a11的值。
解法二:s15-s6=a7+a8+… +a14+a15=9再利用等差数列的下标之和性质得。
9a11=9,求出a11=1
解法二看起来很简单,但技巧性强,学生没办法一下子想到,如果不是求a11而是求a10或其它的,就不能用此法。解法一的通性通法倒是体现数列基本量的解题方法,体现函数与方程的数学思想,能提高学生基本的解题能力,只是运算量会大些,实际上现在的学生运算能力都偏弱,更需要平时训练加强,教师不能为了避繁而设计技巧性强的题目让学生练习,淡化通性通法的熟练掌握,这样做得不偿失,也背离了数学教育的目的。
[1]陈信云.对数学教学中一题多解的选取,中学数学教学参考 [J],2006.(17)
[2]刘瑞美.是亮点还是败笔——由一题多解引出的数学思考,中小学数学 (高中版)[J],2012.(10)

