多尺度近似熵在机械故障诊断中的应用

臧怀刚，李玉奎，刘子豪

(燕山大学 电气工程学院 工业计算机控制工程河北省重点实验室，河北 秦皇岛 066004)

对于不同的机械振动信号[1-4]，由于信号的时间复杂度不同，其熵值也不同，因此可以根据熵值区分不同的信号类型。当机械设备发生故障时，不同尺度下信号的熵值也会发生较大的变化，通过熵值计算可以区分不同的机械故障。

近似熵(Approximate Entropy)是一种度量时间序列复杂性的方法[5]，具有抗干扰能力强、所需数据短等优点，但却只能衡量时间序列在单尺度上的复杂性，而多尺度熵(multi-scale entropy，MSE)可以衡量时间序列在不同尺度上的复杂性[6-7]，因此，将近似熵与多尺度熵相结合，提取不同尺度下的近似熵作为支持向量机的输入，以实现不同机械故障的诊断。

1 近似熵

已知1个包含N点的时间序列{x(1),x(2),…,x(N)},近似熵算法如下：

(1)确定模式维数m，进行相空间重构，顺序提取时间序列中的元素，构成一组维数为m的向量序列

X(i)={x(i)，x(i+1)，…，x(i+m-1)}，

i=1,2,…，N-m+1。

(1)

(2)定义向量X(i)与X(j)之间的距离d[X(i),X(j)]为两者对应元素中最大差值的绝对值，即

d[X(i),X(j)]=max|x(i+k)-x(j+k)|,

k=0,1,…，m-1；i,j=1,2,…,N-m+1。

(2)

(3)给定相似容限r的阈值，统计d[X(i),X(j)]小于r的数目n,并计算其与向量个数N-m+1的比值，记为

i,j=1,…,N-m+1,i≠j。

(3)

(4)

(5)将模式维数m加1，重复以上步骤可得Φm+1(r)。

(6)定义ApEn为时间序列的近似熵，则

ApEn(m,r)=Φm(r)-Φm+1(r)。

(5)

近似熵的值与数据长度、模式维数、相似容限有关。当m=1或2，r=(0.1～0.25)S时(S为原始数据序列的标准差)，计算得到的近似熵具有合理的统计特性[5,8]。为保证进行联合概率重构时得到更多的信息，取m=2；对于相似容限，过大会丢失很多统计信息，过小则造成统计效果不理想，因此选取r=0.2S。

2 多尺度近似熵

多尺度近似熵即不同尺度下的近似熵，计算方法如下：

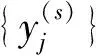
(6)

式中:s为尺度因子。经过粗粒化处理，原始数据序列变为不同尺度s下长度为N/s的粗粒序列。

(2)计算每个尺度下粗粒序列的近似熵，即可获取原始数据在不同尺度s下近似熵的变化。

近似熵反映了时间序列单尺度上的自相关性和复杂程度，熵值越大，时间序列越复杂；熵值越小，时间序列越简单。多尺度近似熵计算的是时间序列在不同时间尺度上的近似熵，反映了时间序列不同尺度下的自相关性、复杂性，以及维数变化时产生新模式的能力，通过对比不同尺度下时间序列的近似熵值区分不同的机械振动信号，非常适合处理非线性机械非平稳信号。

3 试验数据分析

试验数据来自美国西储大学轴承数据中心网站，试验平台由一个1.5 kW的电动机、转矩传感器、功率计等组成，使用电火花技术在轴承上布置单点故障，模拟轴承的4种工作状态：正常、内圈故障、外圈故障及钢球故障。试验轴承型号为6205-2RS，安装在电动机驱动端，通过轴承端的加速度传感器采集振动信号，试验时采样频率为12 kHz，采样点数为2 400。在1 797 r/min转速下,分别测得的正常、内圈故障、外圈故障、钢球故障轴承的振动加速度时域图如图1所示。

图1 振动信号时域波形

由图1可知，由于周围环境和噪声的干扰，直接在时域上不易区分故障类型，因此，选取正常、内圈故障、外圈故障、钢球故障数据各3组，计算原始信号的近似熵，结果见表1。

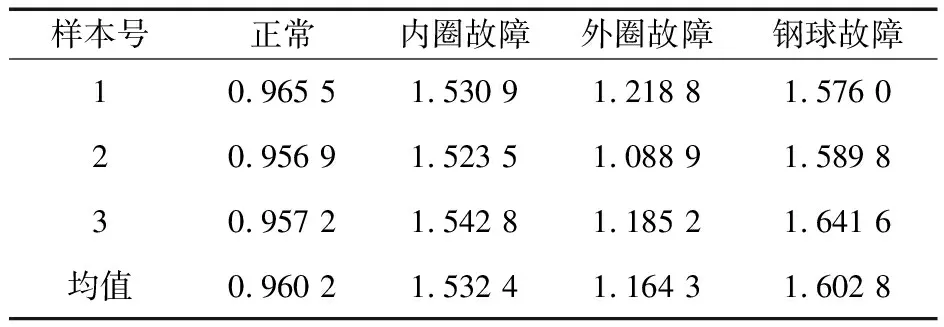
表1 不同状态下轴承振动信号的近似熵

由表可知，同种故障原始信号的近似熵在一定范围内波动，正常信号的近似熵值最小，说明其时间序列的复杂度较低，信号的无序性较低。当轴承发生故障时，信号的时域会有周期性的冲击，近似熵值比正常工况下的大。由于该试验系统采取外圈固定、内圈随轴一起转动，因此内圈的熵值比外圈大。但内圈故障与钢球故障的近似熵值相差不大，区分效果不明显。

计算4种状态下信号的多尺度近似熵，结果如图2所示。由图可知，随着尺度的增加，不同信号近似熵值的差值变大，而且4种信号不同尺度下的近似熵值逐渐稳定，更易区分不同的机械故障。其中，正常信号近似熵值随尺度增加有递增趋势，说明正常信号序列在前几个尺度包含较多信息。

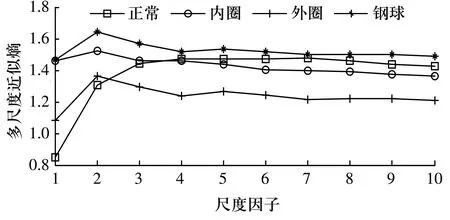
图2 不同状态下的多尺度近似熵值变化曲线

由于前几个尺度的近似熵值包含了绝大部分的故障信号，考虑到支持向量机的输入，选取前5个尺度下的近似熵值作为特征向量，进行SVM训练和测试。分别选取上述4种信号各15组数据进行训练，30组数据进行测试，测试结果见表2。

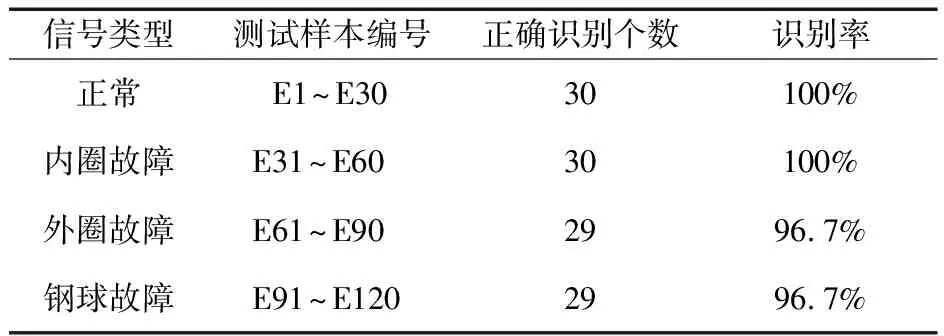
表2 测试样本的识别结果

由表2可知，外圈故障和钢球故障分别有1组数据被错误识别，但总体识别效果较好。说明提取信号的多尺度近似熵进行支持向量机训练和分量，能得到较好的分类结果。

4 实际应用

针对某风力发电机驱动端SKF6326轴承实际信号进行分析。如图3所示，通过安装在发电机前轴承垂直方向的振动加速度传感器采集振动信号，采集仪采样频率为2 500 Hz，采样点数为8 192，发电机转速1 600 r/min时,分别采集正常风机和故障风机同一部位测点的轴承振动信号，时域波形分别如图4、图5所示。

图3 传感器测点布置图

时间/s

时间/s

由于现场环境的各种噪声，直接从时域波形无法区分不同的振动信号。由于实际信号的无序性较高，近似熵值较大，而故障轴承的信号由于存在周期性的冲击，信号有一定的规律，导致其近似熵值有所降低。但2种状态下信号近似熵值相差不大，区分效果依然不明显。因此，计算正常和故障风机下轴承振动信号的多尺度近似熵，结果如图6所示。由图可知，随着尺度因子的增加，正常轴承和故障轴承信号的近似熵的差值逐渐变大，更容易区分不同的机械故障，可判断故障风机发电机前轴承存在损伤。

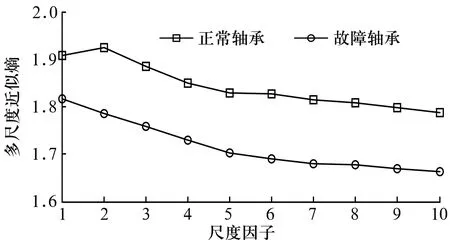
图6 振动信号的多尺度近似熵值变化曲线

由图6可知，对提取信号的多尺度近似熵进行分析，能更好地区分出正常轴承和故障轴承振动信号，可用于判断风机轴承是否存在轴承损伤类故障。但由于实际采集信号受到现场环境等外界条件的影响，不能像仿真试验一样识别不同故障类型，仍需做进一步研究。

5 结束语

用于机械振动信号的故障分析时，多尺度近似熵比近似熵具有更好的抗干扰能力，能够获取更多的故障信息，但存在计算量较大，比较耗时，不利于数据实时分析的缺点。对实际采集信号的分析，也不如仿真分析那样准确，仍需进行深入研究，使其在故障诊断和特征提取方面得到更多的应用。