推力滚针轴承垫圈厚度误差对接触应力的影响
杨晓刚,王旭永,扈文庄
(1.上海交通大学,上海 200030;2.洛阳轴研科技股份有限公司,河南 洛阳 471003;3.河南省高性能轴承技术重点实验室,河南 洛阳 471039;4.滚动轴承产业技术创新战略联盟,河南 洛阳471039)
推力滚针轴承可承受轴向载荷,且承载大,为使轴承不出现“边缘效应”,提高轴承的使用性能和寿命,滚针要经过抛窜使其具有一定的凸度,从而使轴承承载时滚针的接触应力均匀分布。滚针的凸度由窜筒抛窜而成,通过调整窜筒的抛窜方式、时间和磨料的硬度、磨粒大小、比例等因素得到不同凸度形状;推力垫圈由钢板冲压、热处理、抛窜光饰、检验后,直接配对使用[1-3]。
由于该轴承的工况是重载(15 kN)、低速(30 r/min),轴向承受较大载荷,所以滚针和垫圈受力大,对修形和厚度差要求高。文中研究使用对数曲线修形滚针的推力轴承中推力垫圈厚度误差对接触应力的影响。
1 凸度设计
滚针引用对数曲线滚子的曲线方程
(1)
Lwe=Lw-2r;-Lwe/2 式中:y为圆柱滚子的对数曲线函数;x为对数曲线函数的自变量;ν为滚子材料的泊松比;E为滚子材料的弹性模量;Qmax为对数曲线滚子承受的最大载荷;Lwe为对数曲线滚子的有效长度;r为对数曲线滚子端部的倒角半径;Lw为滚子长度。 以推力滚针轴承AXK1230+AS1230为例,其相关参数见表1。 表1 轴承参数 垫圈材料为T8A,滚针材料为GCr15(二者弹性模量和泊松比相同)。 由于推力滚针轴承的结构对称,用有限元分析软件ANSYS建模时,只需分析一个扇区。为提高计算精度,对接触区域进行网格细分,使其为接触半宽(滚针与内外圈的接触矩形)的一半。对下垫圈进行全约束,对上下垫圈、滚针的剖面施加对称约束,如图1所示。 图1 网格模型 滚针没有修形(直素线)的情况下,在15 kN载荷下所得到的接触应力曲线(沿滚针轴向方向)如图2所示。由图可知,在滚针的端部(直线与圆弧连接处)出现了较为严重的应力集中现象,最大接触应力为3 147 MPa。 图2 滚针无修形、倒角0.4 mm时沿轴向接触应力曲线 为避免滚针出现应力集中,使接触应力沿滚针轴向均匀分布,根据理论公式计算出了最佳对数曲线,在15 kN载荷下,滚针素线为对数修形时所得到的接触应力曲线和等效应力云图分别如图3和图4所示。由图可知,滚针最大接触应力为2 789 MPa,接触应力分布均匀、左右对称,且沿滚针轴向向两端缓慢降低。 图3 理想对数曲线修形滚针沿轴向接触应力曲线 图4 理想对数曲线修形滚针等效应力云图 因推力垫圈加工时存在厚度误差,从而使上下垫圈不能均匀地与滚针有效接触,造成各个滚针间的接触应力分布不均,并且随着厚度误差增大,其最大接触应力也增大。厚度误差不能消除,只能控制在一定范围内,在符合产品要求范围内,尽量保持最大公差以降低成本。通过理论分析和试验证明,公差必须控制在0.01 mm内,否则会影响产品寿命。考虑到产品精度要求和经济性,厚度误差从0.006 mm开始分析:1)厚度误差要求过高,很难甚至无法加工,成本会升高;2)厚度误差要求过低,产品无法正常使用。通过检测不同的厚度误差并建立相应有限元模型,得出垫圈与滚针之间的接触应力见表2,接触应力曲线如图5所示。 表2 不同垫圈厚度误差时的接触应力 图5 不同厚度误差时理想对数曲线滚针沿轴向接触应力曲线 由图5可知,随着垫圈厚度误差增大,最大接触应力也增大,并且沿滚针轴向方向接触应力分布极不均匀。滚针左端均出现应力峰值,但当厚度误差为0.01 mm时,滚针左端出现了较大接触应力峰值,为3 307 MPa,接触应力分布也不均匀,但在材料的允许范围之内。 根据GB/T 4662—2010《滚动轴承 额定静载荷》,推力滚针轴承在最大载荷下滚动体和滚道接触中心处所允许的最大接触应力为4 000 MPa。而在一定载荷下,厚度误差为0.01 mm时,滚针与垫圈的最大接触应力为3 307 MPa,但滚针不可能为理想的对数曲线。故综合考虑取安全系数为1.2,即为3 969.1 MPa<4 000 MPa。 在推力滚针轴承寿命试验机上对不同垫圈厚度误差的轴承进行了加载(15 kN)试验,结果见表3。 表3 推力滚针轴承试验结果 为提高推力滚针轴承的使用性能和寿命,滚针为近似对数曲线的推力轴承垫圈厚度误差应控制在0.01 mm以内,以满足实际工况。2 推力滚针轴承有限元模型

3 直素线和对数修形滚针计算结果



4 垫圈厚度误差对对数修形滚针接触应力的影响

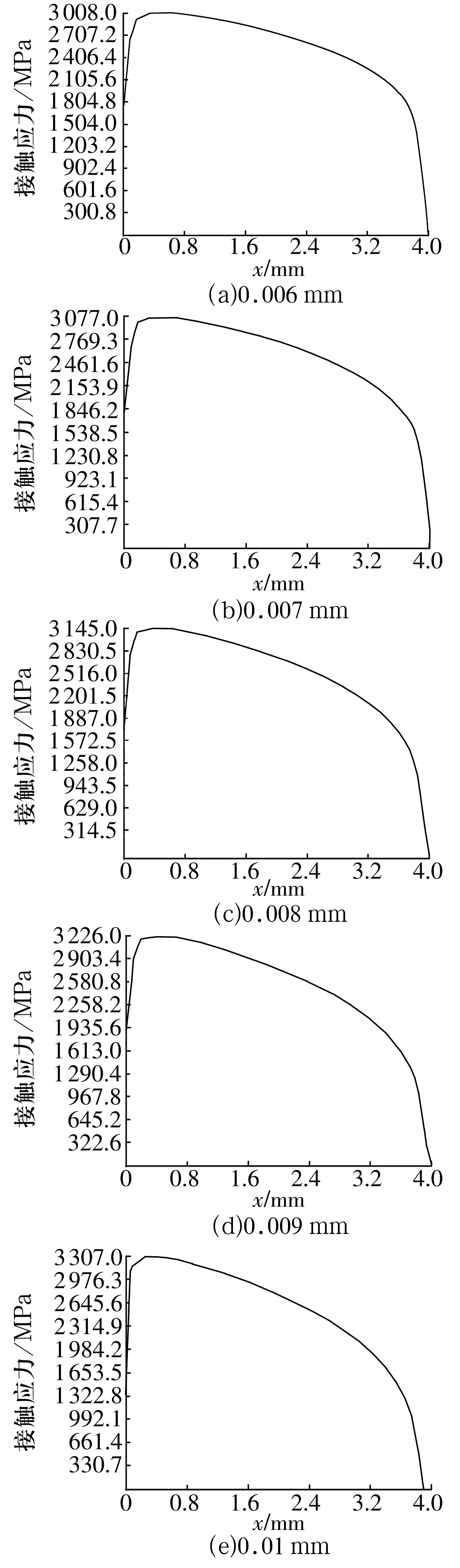
5 试验结果

6 结束语

