基于经验小波变换的轴承故障诊断研究

冯博，李辉，郑海起

(1.石家庄铁路职业技术学院 机电工程系， 石家庄 050041；2.军械工程学院 一系，石家庄 050003)

基于振动信号分析的轴承故障诊断技术的关键是从受噪声污染的振动信号中提取轴承故障特征，其中最常用、最有效的方法就是包络解调技术，而对振动信号作包络谱分析时，一般都采用Fourier变换(FFT)[1]，但FFT只能分析频率不随时间变化的线性平稳信号，且分析结果易受噪声影响，难以取得理想的效果。轴承的振动信号往往是非线性、非平稳信号，常采用Wigner-Ville分布、小波变换等[2]时频分析技术进行处理，但这些方法只能处理相对平稳的信号，当信号的振幅、频率变化剧烈时就有很大的局限性[3]。近年来，基于经验模态分解 (Empirical Mode Decomposition ，EMD)的HHT(Hilbert-Huang Transform)时频分析技术在处理非线性、非平稳信号中取得了比较满意的效果，得到了广泛的应用[3-5]，但EMD不仅缺乏理论推导基础，而且具有端点效应、模态混叠、受噪声影响大、难以分离多个能量相差较大的信号等缺陷[6-7]。为改善EMD的性能，提出了改进措施，例如为避免端点效应，可采用信号延拓方法，为了避免模态混叠，提出了总体平均经验模态分解(Ensemble Empirical Mode Decomposition， EEMD)方法[8]，但EEMD在噪声环境中提取有用信号分量时效果也不太理想，而且还增加了计算负担，延长了计算时间。最近，法国学者Gilles基于小波变换和窄带信号分析理论，提出了经验小波变换(Empirical Wavelet Transform,EWT)，并成功应用于ECG信号分离、图像降噪分析，EWT不仅避免了端点效应、模态混叠现象，而且能从噪声环境中有效提取各个固有模态函数(Intrinsic Mode Function，IMF)分量，不仅提高了信噪比和信号分离的可靠性，而且提高了计算速度，该方法目前在机电设备故障诊断领域还未应用。因此，简要介绍了该方法的基本原理和实现算法，对其不足之处进行了改进，并成功将其应用于齿轮箱轴承的故障诊断。

1 EWT的基本原理

1.1 尺度函数和小波函数

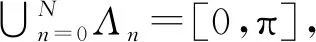
图1 频带分布

每个经验小波定义为在频带Λn内的紧支窄带带通滤波器，根据小波理论，经验小波的尺度函数φn(ω)和小波函数ψn(ω)在频域内分别定义为

,(1)

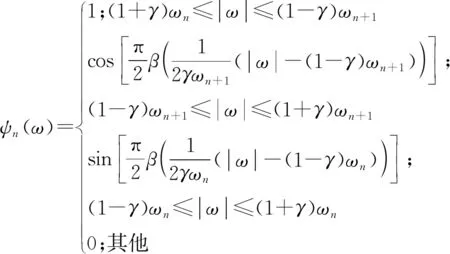
，(2)

β(x)=x4(35-84x+70x2-20x3)，

0<γ<1，τn=γωn。

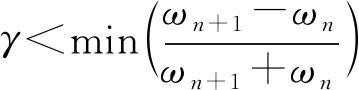
当ωn∈{0,1.5,2,2.8,π}，γ=0.05时，经验小波构成的滤波器组如图2所示。

图2 经验小波构成的滤波器组

1.2 频带边界角频率ωn的确定

设信号x(t)的Fourier变换为x(ω),ω∈[0,π]，依次求出|x(ω)|的前N个极大值，其在频域内对应的角频率记为Ωn(n=1,…,N)，则频带边界角频率为

(3)

这样在频域ω∈[0,π]内，就将信号x(ω)的频带划分为N个带宽不等的区域，每个频带内各包含信号x(ω)的一个极大值，根据图1的频带分布，在ω∈[0,π]内，构成N个窄带带通滤波器Λn，每个窄带滤波器的下截止频率为ωn，上截止频率为ωn+1(ω0=0，ωN=π)。

由于带通滤波器组根据信号x(t)的频率特征计算，因而基于EWT的信号分解具有自适应的特点。

1.3 经验小波变换

根据小波理论和 (1)，(2) 式定义的尺度函数φn(ω)和小波函数ψn(ω)，信号x(t)小波变换的细节系数Wx(n,t)和逼近系数Wx(0,t)可分别定义为信号x(t)与经验小波函数和尺度函数的内积，即

(4)

(5)

则信号x(t)的重构公式为

(6)

式中：〈·〉为内积计算；*为卷积计算。

1.4 基于经验小波变换的信号分解

根据经验小波变换重构公式，信号x(t)可分解为以下固有模态分量

(7)

对于一个时间序列x(t)，经过经验小波分解后可以得到

(8)

即原始数据x(t)可表示为一系列固有模态函数的和。

通过以上分析可知，EWT与EMD相比具有以下不同点：

1)EMD使用循环方式，每次循环只分解出1个固有模态分量，直到最后的残量为单调函数时，筛选结束。而EWT不采用循环方式，而是一次分解出所有的固有模态分量，因而计算速度快。

2)EMD每次循环需确定出x(t)上的所有极大值点和极小值点，并将所有极大值点和所有极小值点分别用三次样条曲线连接起来，将这2条曲线分别作为x(t)的上下包络线，然后筛选出一个固有模态函数，因而受噪声影响大。EWT利用了大多数时域信号在时域内不具有稀疏性，而在频域内具有稀疏性的特点，在频域内寻找函数x(ω)的前N个最大值，并据此划分信号x(t)的各模态分量的频带边界，并充分利用信号的前验知识，可根据需要缩短频带宽度，保证了分解出的各固有模态分量为窄带信号，因而受噪声影响小，既提高了信号分解的可靠性，又保证了能量(幅值)小的信号分量不被能量(幅值)大的信号分量淹没，能保证一次分解出所有的固有模态分量。

2 基于EWT的信号仿真

为验证EWT的有效性，下面用一个仿真信号进行分析，仿真信号解析表达式为

(9)

式中：n(t)为均值为零的白噪声。

由上式可知，仿真信号由3 Hz的余弦信号、调频信号(基频为48 Hz、调制频率为20 Hz)和频率为188 Hz的调幅信号叠加构成，可模拟频率、能量各异的信号分量，以验证EWT的信号分解能力和抗噪性能。

仿真信号各分量的时域图如图3所示，采样点数为1 000，采样频率fs=1 000 Hz，采样时间为1 s。染噪合成信号如图4所示，信号的信噪比为5.488，峰值信噪比为15.109 9。

图3 仿真信号分量

图4 噪声合成信号

为了完成对染噪合成信号分量的分离，对Gilles的频带边界频率的确定方法进行了改进，一是将角频率改为频率，二是通过计算信号的FFT，在频域内自适应地估算出有用信号分量的频率范围，再充分利用原信号的前验知识，对染噪合成信号分量的频率进行有效估计，确定信号滤波器组的边界频率为[6,26,70,186,190](单位为Hz)。在[0，fs/2]内划分为6个频带，构成6个带通滤波器(图5)，为进行信号的EWT奠定基础。

图5 频带划分

仿真信号的EWT处理结果如图6所示，由于图5给定了6个频带，因此EWT将信号分解为6个信号分量c1～c6，其中c1对应仿真信号中3 Hz的余弦分量x1(t)，c3对应仿真信号中基频为48 Hz的调频信号分量x2(t)，c5对应仿真信号中的188 Hz的调幅信号分量x3(t)，而c2，c4和c6为噪声信号分量。则重构信号由c1，c3和c5合成，结果如图7所示。

图6 EWT处理结果

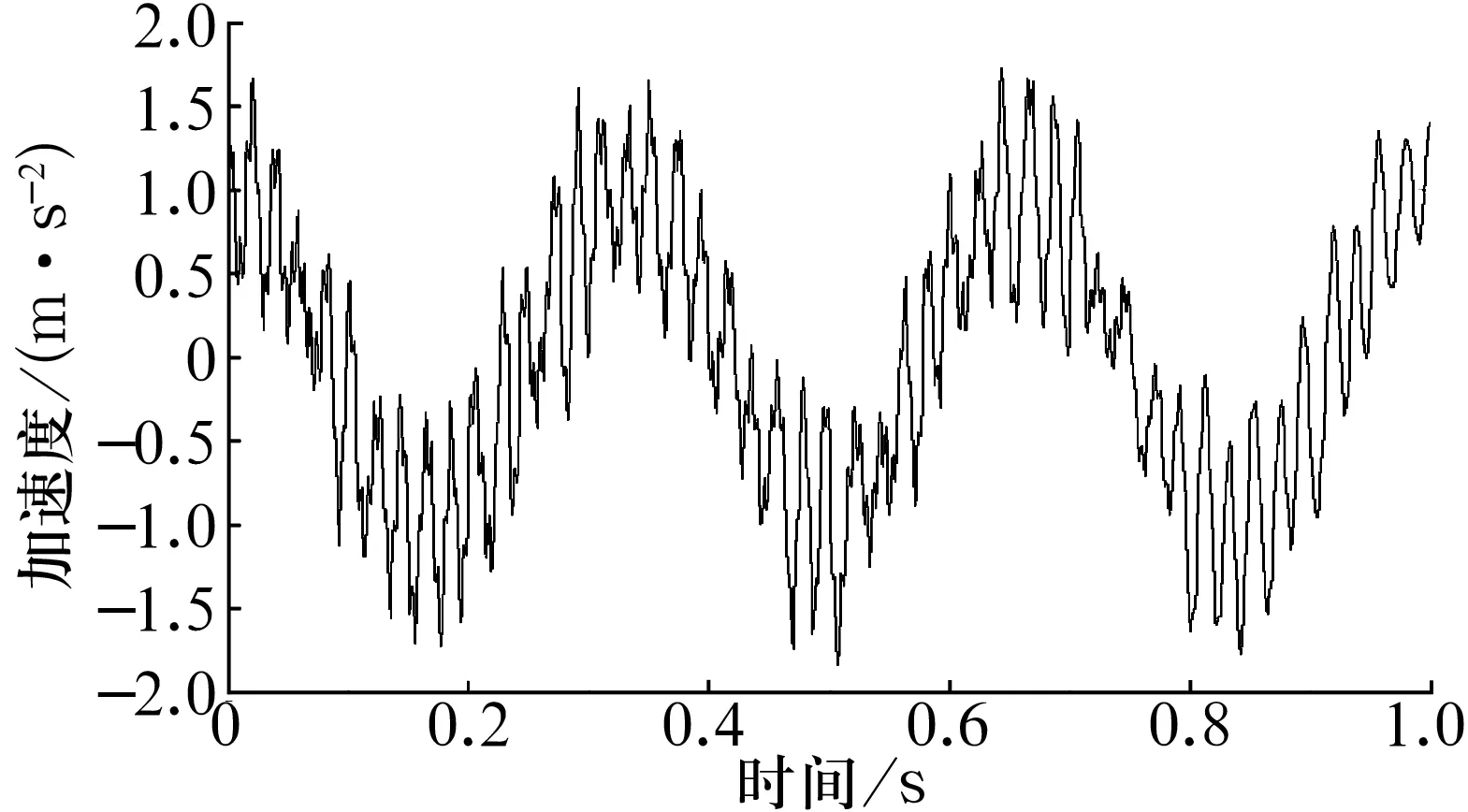
图7 重构信号

从图5～图7可以看出：由于EWT根据信号的前验知识，合理确定了信号分解滤波器组的边界频率，不仅将染噪合成信号中的有用信号分量有效分离，而且去除了信号中的噪声，重构信号的信噪比为13.202 8，峰值信噪比为19.619 2，均方根误差为0.030 5，提高了信号的信噪比。而且能将信号中蕴含的各个固有特征信号分量分解出来，并能有效消除模态混叠的影响，分解出的IMF具有确定的物理意义。

为了验证EWT的有效性，将仿真信号分别进行EMD和EEMD处理，结果如图8和图9所示。由图可知，EMD中的c6及EEMD中的c7和c8分量对应了仿真信号中3 Hz的余弦分量x1(t)，而仿真信号中的调频信号分量x2(t)和188 Hz的调幅信号分量x3(t)由于幅值较小，被完全淹没在噪声信号中，这2种方法均不能有效分离。

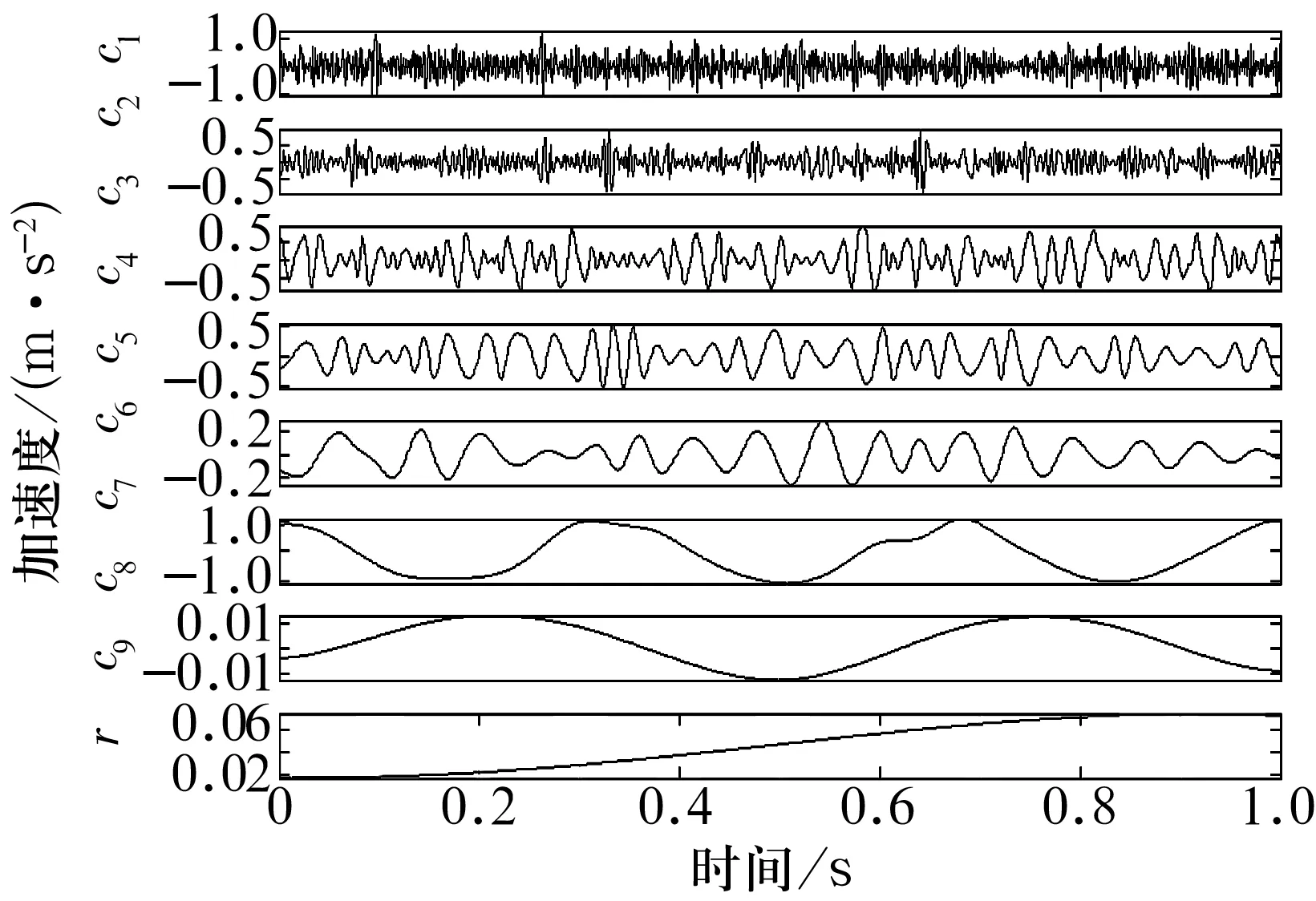
图8 EMD处理结果

图9 EEMD处理结果

另外，3种信号处理方法的计算时间见表1，由表及图可知， EWT从染噪信号中提取有用信号分量的性能优于EMD和EEMD，且受噪声的影响较小。

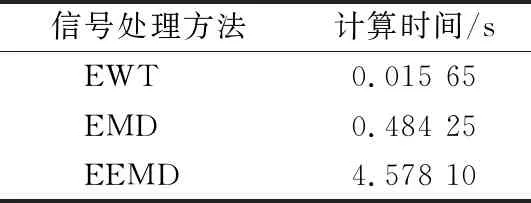
表1 不同信号处理方法的计算时间

3 基于EWT的轴承故障诊断

轴承故障试验数据来源于某型号齿轮箱输入轴轴承，轴承型号为6208(外径80 mm、内径40 mm、宽度18 mm)，在保证使用性能前提下，用线切割技术分别在轴承外圈和内圈各加工深1 mm、宽0.5 mm、长18 mm的小槽，以模拟轴承外圈、内圈局部故障。

齿轮箱振动测试系统采用B&K 3560分析仪，振动传感器为B&K 4508，采样频率为32 768 Hz，采样时间0.25 s。齿轮箱输入轴的转速为1 500 r/min。计算可得输入轴的旋转频率fr、内圈故障特征频率fi、外圈故障特征频率fe分别为25，148.5和101.5 Hz。

轴承内圈存在局部故障时振动信号的时域波形如图10所示。从图中可以看出，在轴承的旋转过程中，内圈故障表面撞击轴承其他零部件的表面，产生幅值较大的高频振动序列，但由于噪声的影响，周期性脉冲序列的故障特征不是十分明显，因此还不能准确确定齿轮箱中局部故障轴承的位置和故障模式。

图10 轴承内圈故障的时域波形

该振动信号经高通滤波后计算的包络谱如图11所示。虽然在图中能够辨别轴承内圈故障特征频率及其二倍频，但由于噪声的影响，不仅分辨率较低，而且fi及其二倍频处不存在以fr为间隔的边频带，轴承内圈局部故障的边带信息模糊，故障特征不是特别明显。

图11 轴承内圈故障的包络谱

轴承内圈故障振动信号的EWT处理结果及各模态分量信号的FFT分别如图12和图13所示。从图中可以看出：c1为低频噪声信号，c3为高频噪声信号，c2中周期性的瞬态冲击比较明显，为轴承内圈的局部故障引起的高频冲击序列。

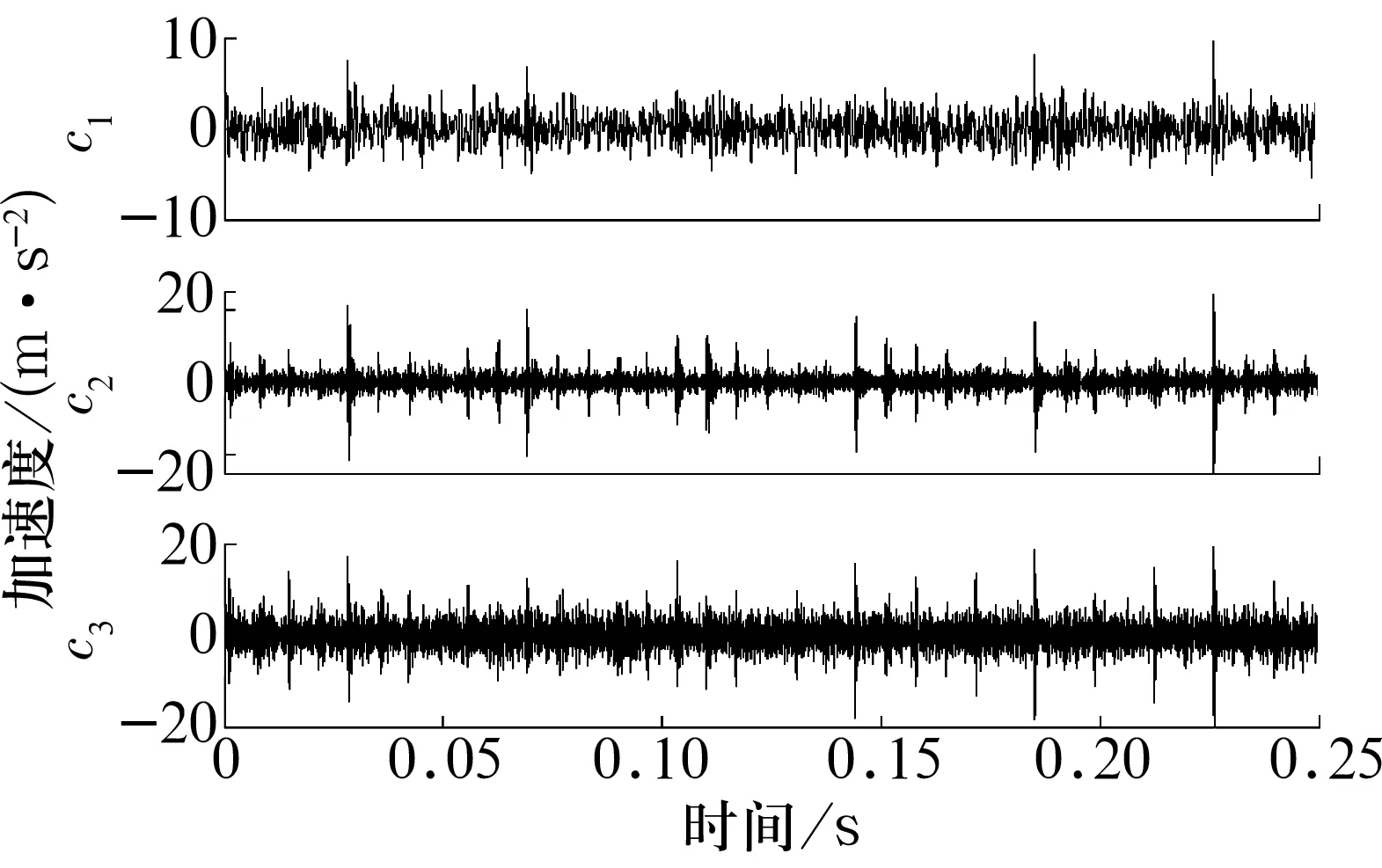
图12 内圈故障振动信号的EWT处理结果

图13 EWT信号分量的FFT

c2分量的包络谱如图14所示。从图中可以看出：具有较大幅值的谱线位于fr及其倍频，以及fi及其倍频处，即在fi及其倍频处存在以fr为间隔的边频带簇，而且fi及其倍频谱线的幅值按指数规律衰减，与理论分析的轴承内圈故障特征相吻合，因此，该频谱结构充分反映了轴承内圈局部故障的频域特征，可以判定为轴承内圈故障。

图14 c2的包络谱

EWT处理后计算的时频谱如图15所示。从图中可以看出，时频谱图很好地表示了因轴承内圈局部故障引起的周期性的瞬态脉冲冲击，瞬态冲击的频率大概分布在3 500～6 500 Hz范围内，瞬态冲击产生的谱线明显且有规律，周期为内圈故障特征周期Ti=0.015 4 s，因此根据EWT时频谱能确定故障轴承的位置和故障模式。图14和图15的试验结果与理论分析相符，从而在频域和时频域内都验证了所提出方法的正确性和有效性，有效提高了轴承局部故障识别的可靠性和准确性。

图15 c2信号分量的时频谱

同理，应用该方法分别对轴承外圈故障、滚动体故障振动信号进行了分析，结果表明：基于EWT的轴承故障振动信号分析方法，能有效从噪声环境中提取轴承外圈及滚动体故障特征，正确识别轴承故障类型。

4 结束语

介绍了基于EWT的轴承故障诊断方法。通过对仿真信号和齿轮箱输入轴轴承内圈局部故障、外圈局部故障试验信号的分析结果表明：基于EWT的时域分析，可获得一系列单分量的固有模态函数，因而能获得各个固有模态函数的幅值、频率等信息, 能有效消除模态混叠的影响，并能有效分离淹没在强噪声信号中的微弱信号分量，提高信噪比，其性能优于传统的EMD和EEMD方法，为从噪声干扰信号中提取轴承故障特征的一种有效方法，能够有效识别轴承故障类型和位置。