塔基移位下架空导线的应力与弧垂研究
孟遂民 周 翔 徐文洋 秦 坤 丁志敏
(三峡大学 电气与新能源学院,湖北 宜昌 443002)
作为电能传输的载体,架空输电线路得到了广泛的应用.但架空输电线路容易受到外界影响(地质环境或人为)致使其发生杆塔塔基移位(倾斜或沉陷),从而导致线路的档距和高差发生变化.线路参数的变化会导致架空导线的应力与弧垂发生变化.过大的应力可能会造成断线倒塔的事故,过大的弧垂会造成导线对地或跨越物的安全距离减小而产生闪络跳闸事故.文献[1-7]对架空导线由于运行工况发生变化与施工过程中的连续档应力与弧垂计算进行了相关研究,但其理论不完全适用于线路参数变化的情况.
本文研究了现有架空导线的力学计算理论,提出了塔基移位下连续档应力的精确求解算法,并编制了相应的计算机软件,能准确地得到线路参数发生变化时架空导线的应力与弧垂,为线路的安全运行与检修提供了理论依据.
1 塔基移位的分类及影响
由于地质环境的变化(如地震、地下水位下降等)或人为因素(爆破、采矿等),造成塔基位置移动或倾斜的现象称为塔基移位.根据塔基位置移动方向的不同,可将塔基移位分为高差移位、纵向移位(线路方向)、横向移位(横担方向)与多向移位(塔基同时在两个以上方向位移)等4种类型,如图1所示.其中纵向移位和多向移位对线路参数有很大影响,高差移位与横向移位对线路的影响较小,本文研究塔基移位中的纵向移位问题.
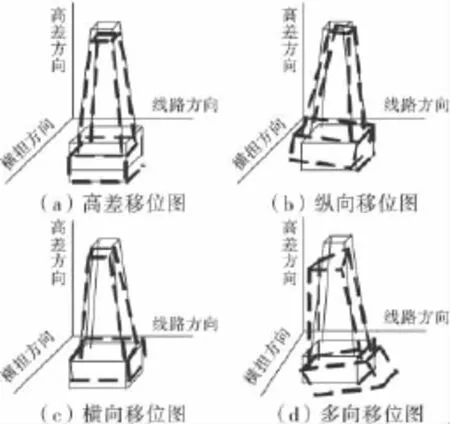
图1 塔基移位示意图
2 塔基移位下导线应力的精确求解
2.1 各档距变化量与导线应力的关系
由于塔基移位,输电线路的一档或多档的档距与高差发生变化,从而使各档导线的应力随之发生改变,如图2所示,其中实线和虚线分别表示线路参数未变化与变化的情况.

图2 塔基偏斜示意图
塔基移位后,假设各档架空导线对线夹未发生相对滑移,档内原始线长不变,由此可以建立档距变化量与架空导线应力的关系.将竣工状态(悬垂串处于铅垂状态)作为第Ⅰ状态,塔基移位后的状态作为第Ⅱ状态,根据两种状态下导线的原始线长相等,可以得到第Ⅱ状态下第i档的档距变化量与导线应力的关系为:
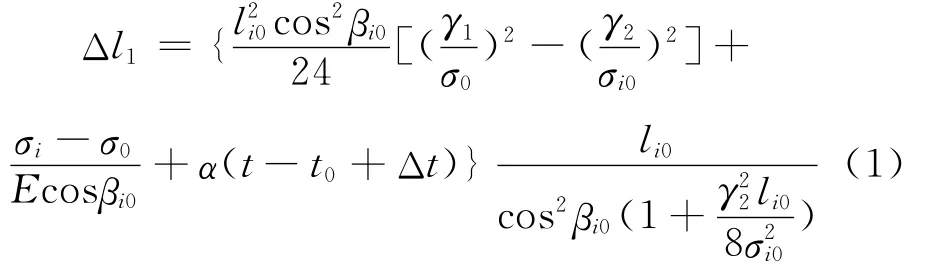
式中,li0、βi0分别为第Ⅰ状态下第i档的档距和高差角;γ1、γ2分别为第Ⅰ、Ⅱ状态下第i档导线的比载;σ0、σi0为第Ⅰ、Ⅱ状态下第i档导线的水平应力;E为导线的弹性系数;E为导线的线膨胀系数;t0、t分别为第Ⅰ、Ⅱ状态下的气温;Δt为补偿导线初伸长降低的温度.
2.2 绝缘子串偏斜引起的线夹偏移量与导线应力的关系
塔基移位后,由于架空导线各档间的应力不等,使悬垂绝缘子串发生偏斜,造成线夹在线路方向上产生偏移.耐张绝缘子串本身近似水平,可认为耐张绝缘子串形变引起的线夹偏移量为0.因此设悬垂绝缘子串为均布荷载的刚性直棒,则第i基杆塔的悬垂绝缘子串受力如图1~3所示.
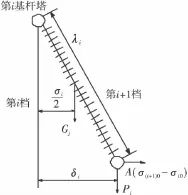
图3 悬垂串受力图
图中λi为悬垂绝缘子串的长度;Gj为悬垂绝缘子串的垂向荷载;Pi为导线作用于悬垂绝缘子串下端线夹上的垂直荷载,可由垂直档距的求得;A(σ(i+1)0-σi0)为左右两档导线的不平衡张力.在不平衡张力作用力下悬垂绝缘子串下端线夹产生偏移量δi.对悬垂绝缘子串上端挂点列力矩平衡方程,有

上式整理可得到悬垂绝缘子串偏移引起的线夹偏移量与导线应力关系为
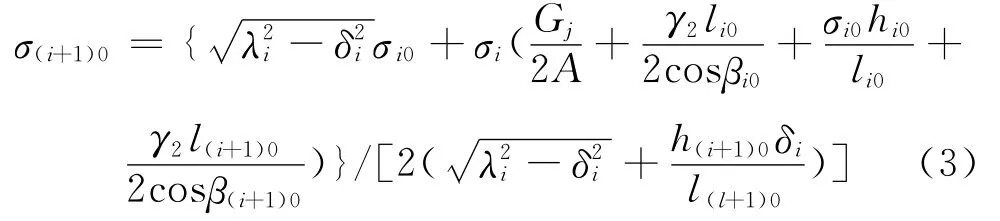
式中,A为导线截面积;hi0、h(i+1)0为第i、i+1档悬点的高差.
2.3 档距变化量、绝缘子串偏斜引起的线夹偏移量及杆塔挂点偏移量的关系
含有n档的连续档以耐张塔为起始杆塔,从0号开始到n号命名,且规定从小号侧往大号侧(顺线路方向)为正方向.设第i基杆塔上绝缘子偏斜引起的线夹偏移量为δi,由于连续档两端均为耐张杆塔,则δ0=0、δn=0.设由于塔基移位,第i基杆塔绝缘子串上挂点产生线路方向偏移量Δxi,则各档档距变化量与δi和Δxi有如下关系:

3 塔基移位下的架空导线弧垂计算
架空导线上任意一点弧垂是指该点距两悬点连线的垂向距离.在塔基移位情况下,计算架空导线上任意一点的弧垂需要考虑绝缘子串与杆塔挂点偏移造成的影响.塔基移位后第i档的导线任意一点的弧垂为
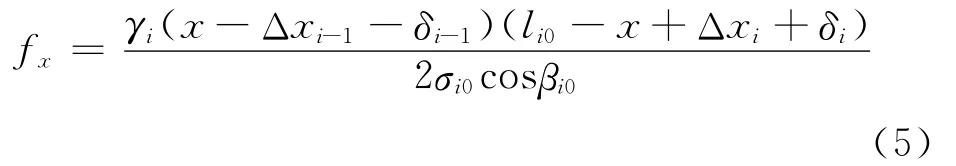
式中,x为导线上任一点到小号侧悬点(塔基移位前)的水平距离.
4 导线应力计算机求解
若一个连续档耐张段内共有n档,则有n-1基直线塔,可列出形如式(3)、式(4)共2n-2个方程,按式(1)可列出n个方程式,总共可列出3n-2方程,已知δ0=0,因此可以迭代求解出σi0、Δli、δi共3n-1个未知量,结合文献[8-10]关于线路力学求解程序可作出导线应力求解流程,如图4所示.求解步骤如下:
(1)假定一个水平应力σ10;(2)由式(1)计算Δl1Δ(li);(3)由式(4)计算δ1(δi);(4)由式(5)计算σ20(σ(i+1)0);(5)按照步骤(2)~(4)可计算出全部σi0、Δli、δi;(6)若求得δn接近于零,则满足要求,上述各结果即可作为计算结果;否则需重新假定σ10,由步骤(1)开始计算直到满足条件为止.

图4 应力求解流程图
5 算 例
某220kV架空输电线路中一耐张段含有10档,位于全国Ⅲ典型气象区,该耐张段的线路参数见表1.导线型号为LGJ-300/40,考虑初伸长降温25℃.架线竣工温度15℃,应力为57.75MPa.悬垂串长为3.115m,自重1 350.68N.假定发生出两种塔基情况,见表2.表2中δl为塔基移位造成绝缘子串上挂点在线路方向的偏移量.现计算塔基移位后年均温气象条件下的各档应力与弧垂.

表1 线路参数
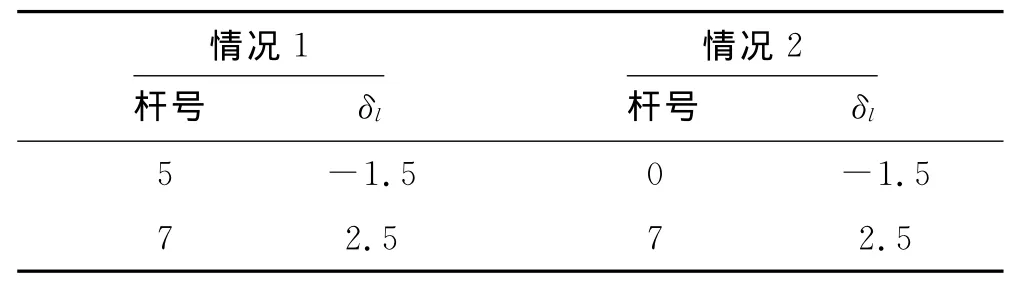
表2 倾斜杆塔参数 (单位:m)
编程计算,界面如图5所示.为便于进行对比分析,对年均温气象条件下的塔基未移位、移位后的情况1、情况2的3种情况分别进行了计算,结果见表3~4.

图5 程序界面图

表3 计算结果(应力)表 (单位:MPa)

表4 计算结果(弧垂)表 (单位:m)
对比塔基移位后的情况1、2与未移位情况,可以看出,塔基移位后应力的最大改变量分别达到7.8 MPa、13.25MPa,弧垂最大变化量分别达到2.19m、3.08m.最大应力分别达到61.725MPa、67.377 MPa,最大不平衡应力差分别为13MPa、6.72MPa,其中情况1中产生的最大不平衡张力达到4 407N.计算得到的最大弧垂变化量(用于判断导线净空距离是否符合运行规范)、最大应力(用于判断运行应力是否在设计安全极限内)和最大应力差(用于判断不平衡张力是否在杆塔和杆塔基础安全运行的极限内),可以与线路设计及运行规范要求进行比较,以此判断塔基移位产生的最大弧垂、最大应力和最大应力差是否满足运行条件,为运行检修提供数据支持.
计算结果表明,同等塔基移位偏移量情况下,耐张杆塔发生偏斜比直线杆塔对连续档的影响更大.这是由于直线杆塔塔基移位,悬垂串能相对补偿档距的变化量,从而减小塔基移位对线路的影响,而耐张杆塔塔基移位时,耐张绝缘子串对线路档距的补偿作用极小,继而造成同等塔基移位情况下耐张杆塔比直线杆塔的影响要大.
计算结果还表明,塔基移位对其相邻5档内的架空导线应力与弧垂影响较大,且对距偏斜杆塔越远档的架空导线的应力与弧垂影响越小.这是由于悬垂串偏斜的补偿引起的.因此,在日常的线路运行维护中应该注重倾斜杆塔杆塔及相邻档的监测,确保线路能安全有效长久地运行.
6 结 论
1)塔基移位的发生位置对连续档的应力和弧垂影响明显,耐张杆发生偏斜比直线杆偏斜对连续档的影响更大.
2)塔基移位对各档的影响随距其档数的增加而减弱,5档之外的影响可以忽略.
3)本文提出的塔基移位下架空导线应力与弧垂的计算方法比较简单,易于编程实现,可用于判定由于塔基移位引起的最大弧垂、最大应力和最大应力差是否满足运行要求.
[1] 邵天晓.架空送电线路的电线力学计算[M].2版.北京:中国电力出版社,2003.
[2] 孟遂民,孔 伟.架空输电线路设计[M].北京:中国电力出版社,2007.
[3] 李博之.高压架空输电线路架线施工计算原理[M].2版.北京:中国电力出版社,2008.
[4] 黄维维.独立挂点双联悬垂绝缘子串在连续上下山时的受力分析及串长调整[J].企业科技与发展,2010,286(16):192-194.
[5] 杨振谷.输电线路连续档导线力学计算方法[J].电力技术,1983(12):17-19.
[6] 张子引,刘学军.架空输电线路连续档不平衡张力计算[J].电力建设,2009,30(5):32-34.
[7] 张 健,秦志清.架空输电线路覆冰不平衡张力的计算与分析[J].机电信息,2013,360(6):146-147.
[8] 聂世明,徐 军.架空输电线路连续上下山以及多耐张段连续紧线的计算机算法[J].内蒙古科技与经济,2010,204(2):122-123.
[9] 黄明琮.连续倾斜档架线的计算程序[J].电力建设,1985(8):20-26.
[10]宋辉梅,刘新闯,马银戌.基于VC++.net的高压架空输电线路的电线力学计算[J].电力科学与工程,2006(3):53-55.

