深海压力补偿电机旋转轴密封性能分析

邓少华 吴正佳 段方立 周玉琼

（三峡大学 机械与动力学院，湖北 宜昌 443002）

水下作业时，潜水电机的密封性和耐压性、水密接头的密封性及绝缘程度，很大程度上决定了该动力源的水下作业深度［1］.据相关资料显示，水下电机的故障发生率很大程度上取决于其密封性能的好坏.

对于水下驱动电机的密封不外乎静密封和动密封两种形式.电机进行压力补偿后，静密封比较容易解决，而电机伸出轴的动密封则是整个电机系统最关键也是最难解决的密封问题.深海电机在工作时，由于电极旋转轴与机壳间存在间隙，会发生泄漏，而且介质压力越高、轴的转速越高，越容易产生泄漏.因此，压力补偿式深海电机轴动密封最关键的问题在于确定深海环境压力对密封件使用的影响.常用的电机转轴的动密封主要有橡胶圈密封、机械密封和磁密封几种形式，鉴于深海复杂的应用环境，深海压力补偿电机试制阶段需尽量减小系统的体积、重量，降低设计成本，而O型密封圈由于结构简单、成本低、工艺性能好等特点，是深海电机旋转轴等工程机械的常采用的密封方式［2］.近些年来，国内外学者采用不同方法对O型密封圈进行了有限元分析，得出了不同条件下的应力分布情况及密封性能的影响因素.关文锦、蒋国璋等［3－5］采用 ABAQUS软件建立 O形密封圈的二维模型，分析预压缩率、介质压力以及结构参数对O形密封圈的密封性能的影响.陈国定、王杰等［6－7］采用有限元法，分析了不同油压作用下O型圈应力分布以及最大接触应力和油压、初始压缩率的关系.但是这些研究大多针对用于液压系统密封的O型密封圈，对于深海电机旋转轴动密封的O型密封圈的相关研究较少.由于深海电机特殊的工作环境，用于其旋转轴动密封的O型圈比液压系统的工况及受力更为复杂，性能要求也更高，因而本文以深海电机旋转轴用O形密封圈作为研究对象，利用ANSYS软件对其进行有限元仿真分析，探究深海高压环境对密封件密封性能的影响是一项有意义的工作.

1 密封圈有限元分析理论基础

O型密封圈是一种截面为圆形的挤压型橡胶密封圈，依靠弹性变形在接触面上产生接触压力从而达到密封的效果.在对深海电机旋转轴进行动密封时，O型圈与密封槽、电极旋转轴之间存在挤压作用，由于其复杂的边界条件，对O型密封圈进行有限元计算时必须将O型圈及密封结构的轴、密封槽作为整体进行分析［8］.而电机轴、密封槽为不锈钢材料，O型圈是橡胶材料，故针对O型圈的有限元分析是橡胶与金属这两类材料的接触问题.

1.1 超弹性体非线性本构理论

橡胶材料被称为超弹性材料或称为Green弹性材料，其特性是各向同性、高度变形和体积近似不可压缩.由于橡胶材料具有非常复杂的特性，在对橡胶材料进行相关力学研究计算时，一般选用应变能密度函数这一标量函数来表征橡胶的力学特性.

为了得到表征橡胶材料一般性质的精确表达式，国内外学者针对橡胶材料提出了许多不同的本构关系，如 Mooney－Revlin模型、Ishihara－Zahorski模型、Klosne－Segal模型、Biderman模型.其中广泛应用的是Mooney－Rivlin模型.

根据其材料参数设定的不同，在有限元分析软件ANSYS程序中，表征不可压缩橡胶类材料的超弹性特性的Mooney－Rivlin模型，可分为2个、5个和9个材料参数的3种模型.本论文采用的2个材料参数的Mooney－Rivlin模型与拉伸实验数据在150%范围内的应变具有较好的相关性，完全能满足橡胶材料实际应用的性能计算需要.其应变能函数如下［7］：

式中，I1、I2为应变张量的2个主不变量；C10、C01为材料常数，依据橡胶材料的弹性模量实验计算得出.

1.2 接触问题的有限元分析方法

接触问题是工程领域中复杂的非线性问题之一，其复杂性表现在接触区域的范围、接触物体的相互位置以及接触的具体状态都是未知的.由于非线性问题的复杂性，除少数简单的问题外，严格的数学、力学求解是非常困难的，实践证明采用有限元法处理非线性问题非常有效［9］.

刚体－柔体的接触，柔体－柔体的接触是一般的接触问题的两种基本类型.传统的ANSYS隐式求解器支持点－点接触、点－面接触、面－面接触这3种接触方式.文中O形橡胶密封圈与电机旋转轴是高度非线性行为的接触，属于橡胶柔体与金属刚体的面－面接触.采用有限元法分析接触问题时，如图1所示，通常将相接触的两个物体A、B分别称为接触体和目标体.

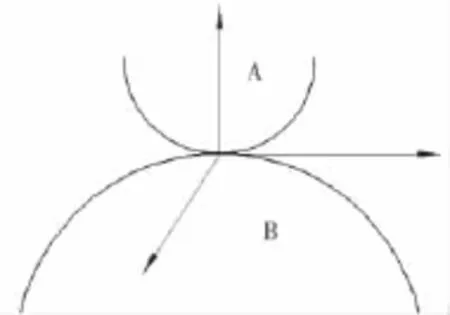
图1 接触物体示意图

本文中O型密封圈作为接触体A，电机旋转轴作为目标体B，其接触抽象为轴对称问题处理.求解接触问题时，需要满足接触物体之间不可相互侵入、接触界面间的法向作用只能为压力以及切向接触的摩擦这三项条件，而且它们都是不等式单边约束［10］.

目前对于接触问题常用的求解方法有直接约束法、罚函数法以及Lagrange乘子法等.本文采用罚函数法与Lagrange乘子法相结合的增强拉格朗日算法来求解O型密封圈与电机旋转轴的接触问题.

2 O型密封圈有限元模型的建立

由于橡胶材料的超弹性，为了使分析能够顺利进行并取得较为精确的结果，在模拟计算过程中做出以下几点假设：1）假设密封结构的重量可以忽略，则在建模时对密封结构采用二维轴对称模型；2）假设密封圈具有确定的泊松比和弹性模量；3）密封圈橡胶材料是不可压缩且连续均匀的；4）由于轴及密封槽壁的刚度远远高于橡胶材料，所以不需要考虑其变形情况.

2.1 单元类型和材料参数的设置

本文深海电机旋转轴用O型密封圈材料为丁腈橡胶（nitrile butadiene rubber，NBR），截面直径为3.55mm，内径为23mm，弹性模量为E＝2.82×106N／m2，泊松比μ＝0.499 9.在有限元软件 ANSYS中O形圈橡胶选用HYPER56超弹性单元和二参数Mooney－Rivlin模型来模拟，材料常数C10、C01分别取值1.87MPa和0.47MPa［11］.电机旋转轴及密封槽这些刚体材料均选用线性实体单元PLANE82，弹性模量E＝2.1×1011N／m2，泊松比μ＝0.3.模型中的接触对为面－面接触，ANSYS建立接触对时自动生成目标单元TARGE169和接触单元CONTACT172.

2.2 几何模型的建立及网格划分

电机旋转轴O型密封圈安装在轴与密封槽之间，边界受力条件具有圆周对称性，根据O型密封圈的结构和ANSYS软件的功能特点，将O型密封圈简化为平面轴对称模型.通过ANSYS中的扩展命令可将平面对称模型的分析结果进行扩展，达到对三维模型进行分析的效果，这样计算结果较好，而且还节约了计算机资源，提高了计算速度.此外，由于轴的刚度是密封圈刚度的几万倍，二者接触时密封圈会发生大变形，轴几乎不发生变形，所以，在建模过程中，轴的截面尺寸大小并不重要，甚至可以用一条线来代替轴面.

采用ANSYS直接建模的方式，构建唇形密封圈与电机轴表面接触的二维平面几何模型.在几何模型建立的过程中，本着尽量忠于结构原始尺寸的原则，取轴的一小部分与密封圈做接触分析.此外，为方便分析，将轴与密封圈的位置调整到刚好接触时的位置上.在对密封结构进行网格划分时，选用适合变形要求的四边形单元，首先采用了自由划分的方式，再对O型密封圈进行网格细化.模型网格划分单元数为7 272个，划分网格后的有限元模型如图2所示.

2.3 接触对的建立及约束和载荷的施加

该模型存在3个接触对，一个是O型密封圈与轴表面的接触，另外两个是密封圈与密封槽的侧面和底面的接触.在这3个接触中，轴和密封沟槽为刚体，密封圈为柔体，故以轴和密封沟槽为目标面，分别以O型密封圈与电机旋转轴、密封槽相接触的外表面为接触面，利用ANSYS中的接触向导直接进行接触对的建立.

图2 O形密封圈有限元模型

根据旋转轴密封圈的实际工况，本文首先通过轴面位移的控制来模拟O型密封圈的安装过程，使O型圈处于初始压缩状态，即对密封沟槽表面进行全约束，约束轴面的纵向位移，同时给轴面一个X正方向的位移，大小为密封圈安装时的过盈量，该值通过其初始压缩率计算得到.然后在此基础上，在O型密封圈的上半部施加内部油液的压力，模拟密封圈在陆地上使用时的加载情况.完成相应计算后，在密封圈上下部分别施加不同海深的海水压力和油压，完成密封圈在深海环境下的受力分析.其中海水压力随海水深度增加而增大，电机采取压力补偿后密封圈两端的压差约为0.2MPa［12］.

3 计算结果及分析

本文根据深海压力补偿电机的工作环境，分别在不同初始压缩率、不同介质压差的情况下对O型密封圈密封性能进行了分析.

图3～4分别是O形密封圈施加位移载荷之后的Von Mises应力云图和接触压力云图.从图中可以看出，密封圈在压缩安装之后，应力集中在密封圈中部靠近轴和密封沟槽的地方；最大接触压力位于O型密封圈与电机旋转轴及密封沟槽相接触发生挤压的部位，这与实际情况相符.

图3 压缩率6%，O形密封圈的Von Mises应力云图

图4 压缩率6%，O形密封圈的接触压力云图

图5是密封圈仅受内部油液压力，即单侧受压状态时的接触压力云图，压力大小为0.2MPa，此时最大接触压力大小为2.372 39MPa，大于密封圈刚安装时的2.216 93MPa，这说明在一定工作压力下，密封圈具有一定的自密封作用，符合实际情况.

图5 单侧压力0.2MPa，O形密封圈接触压力云图

图6是密封圈初始压缩率为6%，环境压力10 MPa、20MPa、40MPa和6 0MPa，并保持内外介质压差为0.2MPa时的接触压力云图.

图6 密封圈初始压缩率为6%，内外介质压差为0.2MPa时，在不同环境压力下的接触压力云图

从接触压力云图可以看出，O型密封圈在受力情况下，其接触压力呈抛物线分布，与理论上的结果基本一致，并且在相同压差情况下，环境压力对O型密封圈的接触压力分布基本没有影响，最大接触压力大小受到的影响也不大.在0.1～60MPa范围内，最大接触压力随环境压力的增大而减小，大小变化分别约为13.14%，可以认为在不考虑其它因素以及误差的情况下，这是高压环境下O型密封圈体积减小造成的.实际应用中，静水压力每增加21MPa，O型密封圈的体积减小约1%，可以通过增大预接触压力（过盈量）、使用硬度更大的橡胶材料来解决这一问题［3］.

为了直观清楚地观察O型密封圈接触压力随深海环境压力的变化，本文利用统计法得到了O型密封圈的最大接触压力与深海环境压力的关系曲线，如图7所示.

图7 压缩率6%，O形圈最大接触压力随环境压力的变化

图8为相应的接触压力与深海环境压力的关系曲线.从图中可以看出，O形密封圈的最大接触压力大小与其初始压缩率及密封压差有关，初始压缩率越大，最大接触压力越大；密封压差越大，最大接触压力越大，这与常压下O形密封圈的使用情况基本一致.

图8 不同条件下最大接触压力随环境压力的变化图

由于采取压力补偿后，密封圈两端的介质压差很小，即工作压力很小，不存在普通环境下工作压力较大时出现的密封圈挤出现象，因此，可以采用目前普遍采用的O形密封圈失效判据式来判断密封情况.

其中，Pmax为最大接触压力；ΔP为密封件两端介质压差.

根据图8不同条件下最大接触压力随环境压力的变化图可以看出，在不同的环境压力下，O形密封圈的最大接触压力值虽然不同，但始终大于其工作压力（介质压差），保证了密封性能.这说明深海环境压力对压力补偿后的O形密封圈密封性能影响不大.

4 结 论

本文利用ANSYS软件对深海环境下压力补偿电机旋转轴使用的O型密封圈进行了有限元分析，更直观地了解了密封圈在高压环境下的密封性能.分析结果表明，采用对O形密封圈施加压力来模拟深海环境的计算方法是合理的，相关结论如下：

1）利用ANSYS软件采用非线性方法模拟计算深海环境下O形密封圈的变形及接触压力情况，为深海压力补偿电机旋转轴的动密封性能研究提供了一条更直观的途径.

2）通过有限元计算结果可以看出，外界环境压力对深海环境中使用的O形密封圈接触压力影响不大，与普通常压下的使用情况基本一致，但与密封圈压缩率及两端介质压差的大小有关，可以用于压力补偿后的动密封场合.

3）接触压力在O形密封圈接触宽度上呈抛物线分布，在接触面中部达到最大，向两侧呈逐渐减小的趋势.这为深海环境下O型密封圈的设计与使用提供了参考.

［1］ 刘子俊，崔皆凡.海洋机器人用水下电机的深水密封研究［J］.机器人，1997，19（1）：61－64.

［2］ Heing K.Maller，Bemand S.Nau.Fluid Sealing Technology Principlesand Applications［M］.Cheng Chuanqing translation.Mechanical Engineering，2002.

［3］ 关文锦，杜群贵，刘丕群.橡胶O形圈密封性能的有限元分析［J］.润滑与密封，2012，37（6）：60－64.

［4］ 蒋国璋，陈少华，谢良喜，等.O形旋转密封圈的密封性能有限元分析［J］.机械设计与制造，2014（6）：178－181.

［5］ Hu Congfang，Tan Yuanqiang.Finite Element Analysis of Tandem Rubber O－ring Sealing Structure at the End of Shaft［J］.Advanced Materials Research，2013：25－29.

［6］ 王 杰，谢禹钧.关于橡胶O形密封圈的ANSYS分析［J］.辽宁石油化工大学学报，2008，12（4）：48－50.

［7］ 尚付成，饶建华，沈钦凤，等.超高液压下O形橡胶密封圈的有限元分析［J］.液压与气动，2010（1）：67－70.

［8］ 周志鸿，张康雷，李 静，等.O形橡胶圈应力与接触压力的有限元分析［J］.润滑与密封，2006，176：86－89.

［9］ 尚晓江.ANSYS结构有限元高级分析方法与范例应用［M］.2版.北京：中国水利水电出版社，2008.

［10］孟永奇，宋 宏.浅谈潜水电动机动密封技术［J］.机械管理开发，2009，24（2）：19－20.

［11］王 伟，邓 涛，赵树高.橡胶 Mooney－Rivlin模型中材料常数的确定［J］.特种橡胶制品，2004，25（4）：8－10.

［12］严 亮，王子荣，金九大，等.低粘度、柔性环氧树脂灌封料在微、轻、薄力矩电机中的应用［J］.微特电机，2005（9）：44－45.