双喷嘴水平对置撞击流混合器内湍流流动及混沌特性

张建伟，董鑫，马红越，冯颖

（沈阳化工大学能源与动力工程学院，辽宁 沈阳 110142）

撞击流（impinging streams，简称IS）概念于1961 年由白俄罗斯的科学家Elperin 首先提出[1]，其特点是可显著强化气固、气液、气气以及液液系统的热、质传递过程。撞击流技术具有促进微观混合和强化相间传递的特点，并且还在制取超细粉体方面的性能优于普通搅拌槽混合器[2]，在燃烧、干燥、粉碎、研磨和吸收方面也产生良好的效果[3]。撞 击流混合器是一种新型高效的反应、混合设备， 其内部流场的运动行为与上述现象有着紧密的 关系。

混合设备内强化动量传递过程往往与其流场特性密切相关，只有掌握了设备内的流动规律才能有效地分析流体微团之间的混合和传递特性。因此，撞击流混合器内流场特性研究备受关注。考虑到撞击流混合器具有优良传质与传热行为的关键是两股流体高速撞击形成径向流动强化流体微团湍动和混合，通过对撞击流混合器内压力波动信号和浓度值的瞬态特性进行研究，发现混合器内的瞬态流动具有明显的非线性特征[4-7]。本文作者前期研究表 明[8-10]，基于混合器内各种波动信号的小波分析和分形理论认识到反应器中流体动力学行为的自相似分形特征和复杂性特征。由于撞击流混合器内流域的非线性很大程度体现在混合器内瞬时速度场的波动，因此研究撞击流混合器内湍流流动及混沌特性具有重要的实际意义。本工作根据激光多普勒测速仪测得的速度场，利用湍流理论计算得到湍流特性参数，并且利用重构相空间理论恢复速度信号的吸引子，进而得到混沌特征参数，研究了撞击流混合器结构参数以及进口处雷诺数对湍流流动及混沌特性的影响。

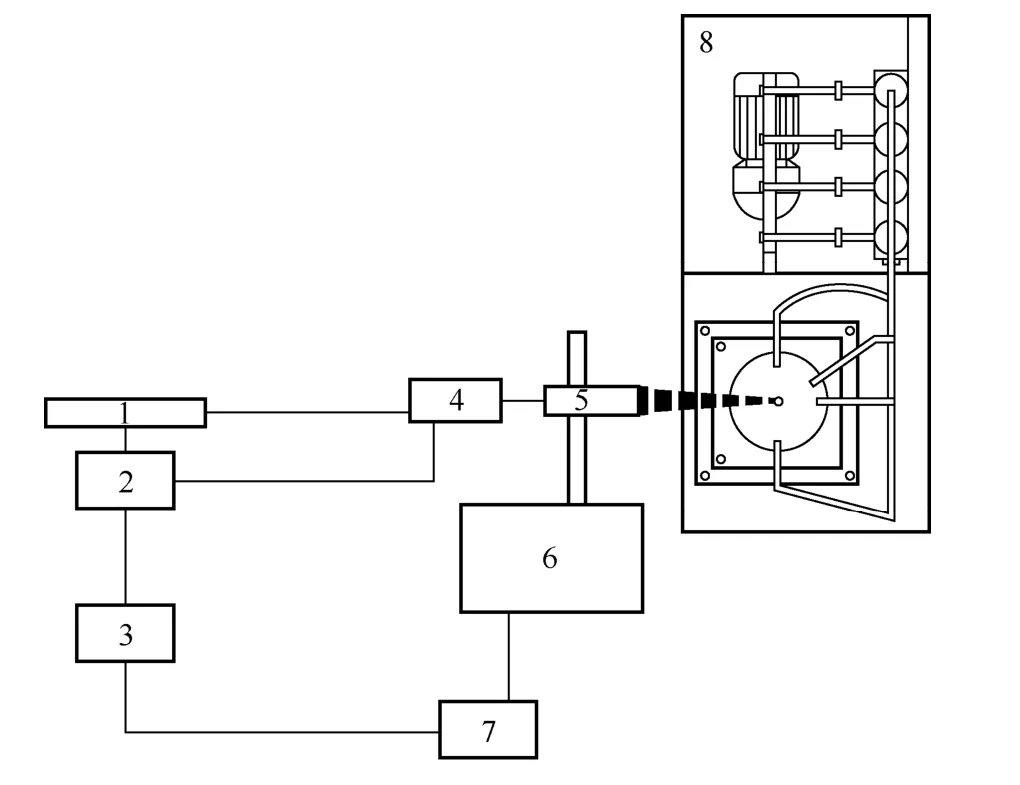
图1 实验测量系统示意图

1 实验装置与测量

1.1 流场测量系统

采用激光多普勒测速仪测量了有机玻璃筒和喷嘴组成的双喷嘴对置撞击流混合器内的流场，实验系统流程如图1所示，有机玻璃圆筒直径为140mm，壁厚为5mm，高为500mm，喷嘴固定在有机玻璃筒两侧中间位置。实验装置是由泵、蓄水箱、转子流量计、阀门、双喷嘴水平对置撞击流混合器以及其连接管线组成的介质循环系统，采用由丹麦DANTEC 公司生产的三维五光束多普勒测速仪对瞬时速度场进行测量，此测速仪则由2017 型水冷氩离子激光器、多色激光束分离器、三维五光束光学发射接收探头、光电接收器、三维信号处理器、三维移动坐标系统和主控计算机组成。在混合器外部设置有方型夹套，在夹套内注入水以补偿折射的影响，可以减小因为折射引起的测量误差[11]。实验所用介质选取蒸馏水，配有示踪粒子，示踪粒子为空心玻璃球，其密度为1.05～1.15g/cm3，直径为10～15μm。

1.2 实验装置介绍

为便于实验测量，坐标系选取直角坐标系。以两对置喷嘴轴线中点为原点，两对置喷嘴轴线方向为x 轴，两对置喷嘴水平径向为y 轴，有机玻璃筒体轴线方向为z 轴，如图2 所示。通过撞击流体入口b1,2不断注入流体，液体排净口c 处于关闭状态，待流体液面位于对置喷嘴上方并保持浸没状态开始进行实验。文中实验的喷嘴间距设定为1d、3d 和5d，进口处雷诺数Re 分别为6050、7260 和8470。其中d、L 和分别表示喷嘴直径和喷嘴间距。

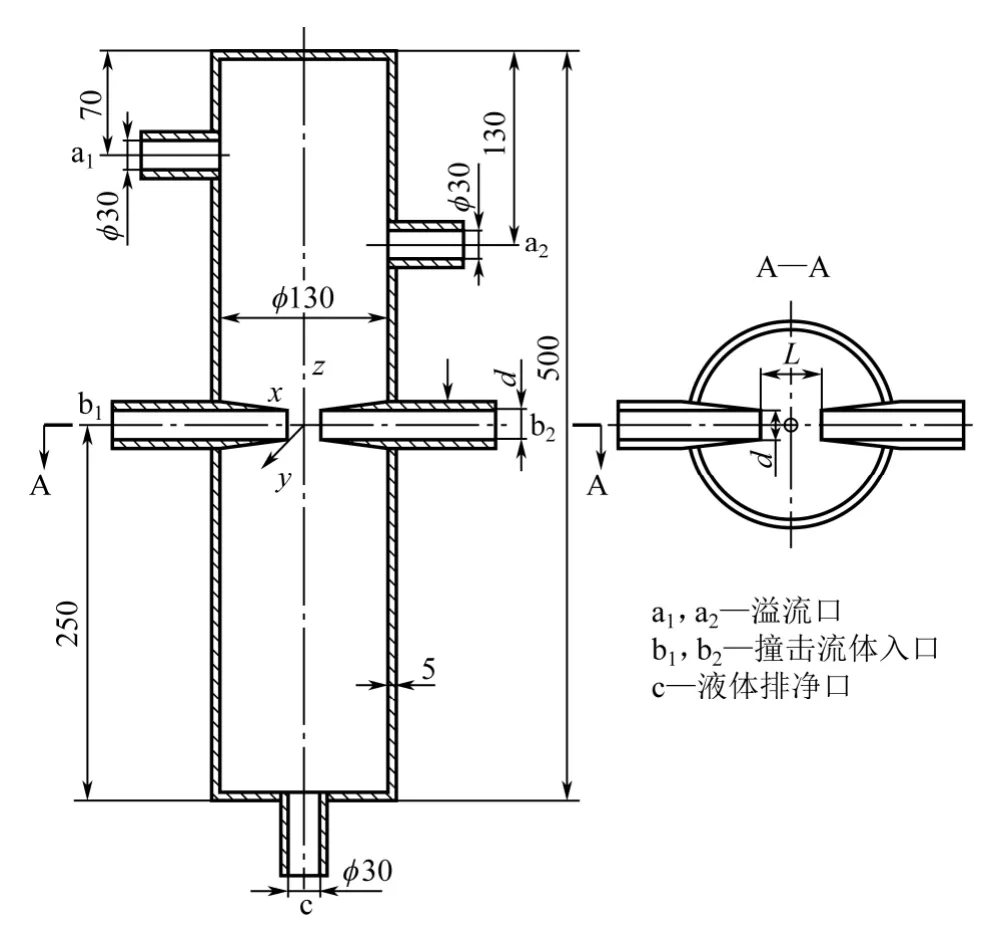
图2 实验装置示意图（单位：mm）

2 撞击流混合器内的流动特性分析

2.1 混合器内速度场的分析

实验采用激光多普勒测速仪测量了进口处雷诺数Re 为6050 时喷嘴间距L 分别为1d、3d 和5d 的撞击流混合器内瞬时速度场。比较坐标系下量纲为1 的径向速度在撞击面中心线上的分布，如图3 所示。由于两股流体碰撞后，流体的运动形式转变成径向射流，即沿着z 轴两侧方向分布，其速度分布趋势关于直线z=0 近似反对称。点z=0 附近区域速度近似为零，形成驻点，可视为撞击中心区。由于喷嘴间距较小时，两股流体撞击不完全，能量传递不明显，而喷嘴间距较大时，两股流体撞击前产生能量损失，碰撞时速度变化较大，但是产生的径向速度不大。所以随着喷嘴间距的增加，径向速度先增加后减小。L=3d 为较适宜的喷嘴间距。

实验测量了喷嘴间距L 为3d、雷诺数Re 分别为6050、7260 和8470 的撞击流混合器内速度场。对比坐标系下量纲为1 的径向速度在撞击面中心线上的分布如图4 所示。与图3 的径向分布相同，由于两股流体碰撞后形成沿z 轴两侧方向径向射流， 其速度分布趋势关于直线z=0 近似反对称。而且在点z=0 附近区域速度近似为零，随着雷诺数的增加，量纲为1 的径向速度呈递增趋势。这是因为雷诺数较大时，两流体射流速度较大，在碰撞时产生的较大的能量传递，从而使径向速度逐渐增加。

图3 不同喷嘴间距下的径向速度

图4 不同雷诺数下的径向速度

图5、图6 分别为量纲为1 的轴向速度在截面中心线上各点不同喷嘴间距和不同雷诺数下的对比结果。其分布规律基本相似，都近似关于直线z=0对称，在点z=0 附近达到各自的极小值，此处为驻点。如图5 所示，由于喷嘴间距较小时，两股流体撞击不完全，能量传递不明显，而喷嘴间距较大时，两股流体撞击前产生能量损失，碰撞时速度变化较大，但是产生的轴向速度不大。所以随着喷嘴间距的增加，轴向速度先增加后减小。L=3d 为较适宜的喷嘴间距。图6 中，随着雷诺数的增加，量纲为1轴向速度呈递增趋势。随着雷诺数的增加，轴向速度逐渐增大。

从图3～图6 可以看出，截面内无因次化轴向速度和量纲为1 化径向速度的分布形式有明显的区别。而不同喷嘴间距和不同雷诺数下轴向速度的分布形式相同，径向速度亦是如此。

图5 不同喷嘴间距下的轴向速度

图6 不同雷诺数下的轴向速度

2.2 混合器内流体的湍流流动特性

2.2.1 湍流特性描述参数

在湍流状态下，流场中任意一点的速度是脉动的。描述湍流流场中某点速度时，通常用时均速度来表示这一点的运动速度，而描述流场湍流特性时，一般用与脉动速度相关的参数来表示，常用的有速度脉动均方根（RSM）、湍流强度、湍动能等。这些参数的表达式分别为式（1）～式（4）。

图7 不同喷嘴间距下的湍流特性参数

2.2.2 不同喷嘴间距对湍流参数的影响

为了具体说明喷嘴间距的变化对撞击流混合器内径向速度场的影响，现对撞击面上沿z 轴方向x=0处的湍流特性参数进行研究。径向速度脉动均方根、湍流强度、湍动能随喷嘴间距变化的趋势图如图7所示（其中，喷嘴间距L 分别为1d、3d 和5d）。

图7(a)是不同喷嘴间距下径向速度脉动均方根沿z 轴的分布曲线，其分布规律基本相似；分布曲线都关于直线z=0 近似对称，在点z=0 附近达到各自的极小值。速度脉动均方根随着喷嘴间距的增加，呈先增加后减小的趋势。这是因为喷嘴间距较大时，撞击速度较小，撞击较不剧烈，间距过小，撞击不完全，可以得到利于混合的合适的喷嘴间距。

在图7(b)中，各个喷嘴间距下的湍流强度分布规律相似，即关于z=0 反对称，都在径向z=-10～25mm 之间的湍流强度有明显的变化。随着喷嘴间距的增加，其值亦先增加后降低。

由图7(c)可知，湍动能的分布规律与径向速度脉动均方根的分布相近。其分布规律基本相似：分 布曲线都关于直线z=0 近似对称，在点z=0 附近达到各自的极小值，并且湍动能随着喷嘴间距的增加，其值亦先增加后降低。分析主要是喷嘴间距增加使径向速度脉动被弱化所致。

2.2.3 不同雷诺数对湍流参数的影响

为了具体说明雷诺数的变化对撞击流混合器内速度场的影响，现对撞击面上沿z 轴方向x=0 处的湍流特性参数进行研究。径向速度脉动均方根、湍流强度、湍动能随雷诺数变化的趋势图如图8 所示（其中，雷诺数Re 分别为6050、7260 和8470）。

图8(a)是不同雷诺数下径向速度脉动均方根沿z 轴的分布曲线，其分布规律基本相似；分布曲线都关于直线z=0 近似对称，在点z=0 附近达到各自的极小值。而速度脉动均方根随着雷诺数的增加，峰值分别为0.14m/s，0.15m/s 和0.22m/s，峰值分别为0.14m/s，0.15m/s 和0.22m/s，其速度脉动呈增大趋势，尤其雷诺数Re=8470 对应的径向速度脉动均方根较其他两种情况下的脉动均方根有明显变化。这是因为雷诺数较大时，撞击速度较大，撞击剧烈。

图8 不同雷诺数下的湍流特性参数

在图8(b)中，不同雷诺数下的湍流强度分布规律相似，即关于z=0 反对称，都在径向z=-10～30mm之间的湍流强度有明显的变化，其余位置对应的湍流强度变化幅度不大。随着雷诺数增大，湍流强度也随之增大；表明此时雷诺数增加对湍流的强化作用增强，分析主要是由于雷诺数增加使速度脉动被大大强化所致。

由图8(c)可知，湍动能的分布规律与径向速度脉动均方根的分布相近。其分布规律基本相似；分布曲线都关于直线z=0 近似对称，在点z=0 附近达到各自的极小值。湍动能随着雷诺数的增加，其增加的幅度比脉动速度增加的幅度更大。分析主要是雷诺数增加使径向速度脉动被强化所致。增加雷诺数可增加高湍动能分布区域，该区域更有利于物料混合。

2.3 混合器内流体的混沌特性

2.3.1 混沌理论

混沌理论在径流预报[12]、经济预测[13]、通信信号调制识别[14]等领域中得到广泛应用，并显示出独特优点，并且近年来应用于内部流场的分析。分析混沌时间序列，首先需要进行混沌特性识别，其主要方法是通过计算混沌信号奇异吸引子的特征参数来辨别，关联维是吸引子维数及其几何结构复杂程度的表征，Kolmogorov 熵则是关于混沌系统的初始信息损失速率的度量，对动力学复杂性的度量描述，最大Lyapunov 指数刻画混沌轨道的局域不稳定性和对初始条件敏感依赖性的定量判据。

首先采用由Packard 等[15]提出的相空间理论重构出瞬时速度信号的吸引子，利用适用于实验观测数据且计算方法简洁的G-P 算法[16-17]对分数维的值进行计算。然后，选用Grassberger 和Procaccia[18]根据q 阶Renyi 熵[19]提出的关联熵K 的算法来估计K 熵。最后，选用Wolf 方法[20]对最大Lyapunov 指数进行估值计算。

2.3.2 重构相空间的参数选取

延迟时间τ 是平衡重构相空间各点间独立性与相关性的重要参数，若延迟时间τ 过大，则各向量之间无相关性，而若延迟时间τ 过小，重构相空间中的各点不能作为独立向量应用于计算。互信息法既评价信号的独立性，也考虑了线性相关与非线性相关对信号的影响[21]，并且互信息法的有效性得到众多相关研究的证实[22]，所以应用互信息法计算延迟时间。

为了令重构吸引子等价于原吸引子拓扑，应该确定最佳嵌入维数。若嵌入维数过小，吸引子则不能容纳系统的吸引子，导致系统的动力特性不能全面展示；若嵌入维数太大，可能将噪声引入到额外的维数上，从而增加额外的计算量和计算难度。因此需要确定恰当的嵌入维数。为确定最佳嵌入维数和线性区间，现选择流场内（0，27，-38）位置处的瞬时速度，根据嵌入维数从1递增到12进行计算，得到关联积分分布曲线图9(a)所示。

图9 不同嵌入维下关联积分曲线和关联

图9(a)中所示的曲线分别为嵌入维数m 由1 至12（从上至下）对应的关联积分曲线，随着关联维数增加，图中的关联积分曲线均收敛于同一斜率，可初步确定此非线性系统的混沌吸引子的收敛性。在图中ln r ∈[ - 2.5, - 1.8]区间内的大多数关联积分曲线，均具有相对一致的斜率，则可以认定该区间为线性区间，并且其中存在关联维。在线性区间内，拟合各点对应不同嵌入维数的关联积分曲线的斜率，然后获得不同嵌入维下的关联维值。利用该方法即可计算撞击面上不同位置处的5 个点的关联维，从而得到各点对应各阶嵌入维下的关联维值如图9(b)所示。嵌入维m≤8 下各点关联维值随m 的增加呈线性增大，显示出一致性，而嵌入维m≥9时，由于嵌入维过大，导致关联维值在撞击区气泡的干扰下出现不稳定的波动。因此，本文均按嵌入维m=8 计算混沌特征参数。

2.3.3 不同喷嘴间距对混沌特性的影响

进口处雷诺数Re 为6050、喷嘴直径为12mm时，分别在两喷嘴间距L 为1d、3d、5d 时，对撞击面进行PDA 测量，计算所有测量点轴向瞬时速度的混沌特征参数：关联维、Kolmogorov 熵和最大Lyapunov 指数，结果如图10 所示。为确定不同的 喷嘴间距对流场混沌特征参数大小的影响，本文作者取不同喷嘴间距下同一直线处各点的混沌特征参数进行对比，如图11 所示（测量点的轴向和垂直径向坐标分别为x =0mm、z =-22mm）。

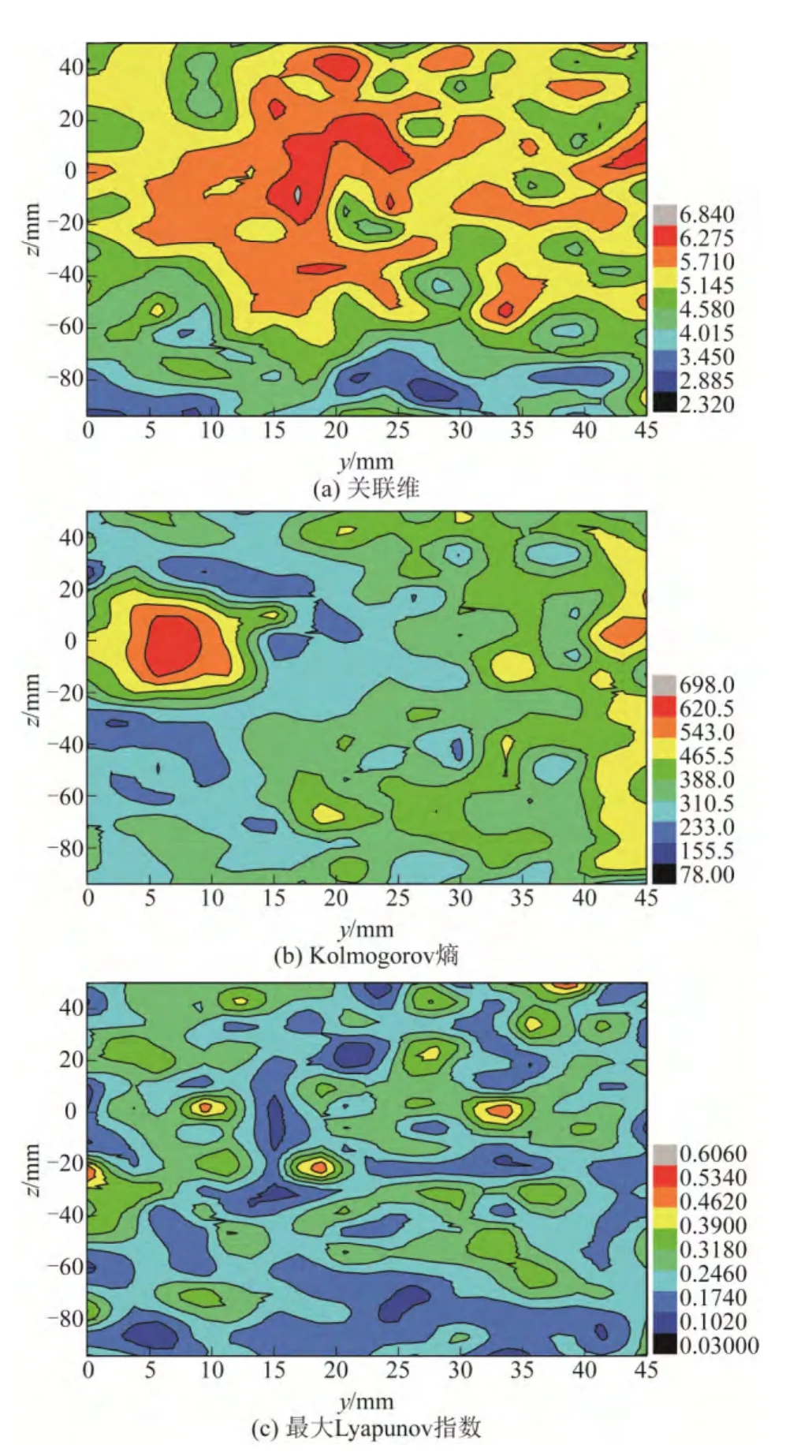
图10 喷嘴间距L=1d 时撞击面的混沌特征参数

在图10(a)中，关联维值在2.32～6.84，同样可以得出此工况下流场具有自相似结构且存在分形。同时在撞击面上从z =30mm 到z =-60mm 区域内的关联维值普遍高于z <-60mm 的区域，说明此区域各点流体的运动行为比较复杂，因为当两股流体相向高速流动撞击时，反复做减幅振荡运动，同时由于撞击过程是在浸没状态下进行，因此两股流体的震荡运动会改变其周围流体的流动状态，从而导致此区域内大部分流体的运动行为比较复杂，关联维值偏大。可以判断该区域为撞击流混合器的撞击区。

图10(b)中，在z =10mm 至z =-10mm、y=5mm至y=10mm 区域内（红色环形区域）Kolmogorov熵最大，此区域流体的初始能量以较大的速率耗散，可认为该区域是两股流体在浸没状态下的撞击中心面。因为两股高速湍动流体剧烈撞击后，改变原有的运动趋势，由轴向运动转化为径向运动并向四周扩散，因此原有的流动状态减弱变为其他形式的流动状态，促使两股流体达到彼此干扰、混合的状态。在撞击面上从y=40mm 至y=45mm 区域内（黄色区域），其Kolmogorov 熵明显略大于除撞击中心面的其他区域，此处是由轴向流动转为径向流动的流体经扩散后碰撞混合器壁面，随后做反向运动并与向壁面方向扩散的流体发生二次碰撞而消耗能量所引起的，此时也起到了二次混合的效果。因此，通过观察整个撞击面上Kolmogorov 值分布状况，可以得到混合器内流场速度信息耗散率较大的区域，同时验证了撞击流混合器内流体的流动趋势。

图10(c)中，整个撞击面上各点的Lyapunov 指数值都大于零，证明该撞击流混合器的流场具有混沌特性。纵观整个撞击面上的Lyapunov 指数值，其数值分布比较均匀，说明整个撞击面内测量点的速度对初始条件均比较敏感，依赖性较大。

图11 结果显示，混沌特征参数（关联维、Kolmogorov 熵和最大Lyapunov 指数）的3 个数值均随喷嘴间距的增大，呈现出相同的变化规律。当喷嘴间距L 由1d 增加到3d 时，3 个数值均明显增大，这是因为随着喷嘴间距的增大两股流体撞击的接触面积增大，从而两股流体的初始信息损失速率增大，这有利于微观混合。当喷嘴间距再次增加到5d 时，3 个数值却明显减小，这是因为当喷嘴间距增加到一定距离，两股流体相撞的剧烈程度减小，产生的震荡程度削弱，不利于微观混合的进行。因此，当喷嘴间距L 为3d 时，此撞击流混合器的微观混合效果最好。

2.3.4 不同雷诺数对混沌特性的影响

喷嘴间距L 为3d，喷嘴直径为12mm 时，进口雷诺数Re 分别为6050、7260 和8470，对撞击面进行PDA 测量，计算所有测量点轴向瞬时速度的混沌特征参数：关联维、Kolmogorov 熵和最大Lyapunov 指数，结果如图12 所示。为确定不同的喷嘴间距对流场混沌特征参数大小的影响，本文作者取不同雷诺数下同一直线处各点的混沌特征参数进行对比，如图13 所示（直线上各测量点的轴向和垂直径向坐标分别为x = 0mm、z =10mm）。

图11 不同喷嘴间距下撞击面的混沌特征参数

图 12 中关联维、Kolmogorov 熵和最大Lyapunov 指数三者的数值云图与图10 具有大致相同的分布规律，此工况下流场具有自相似结构且存在分形，证明该撞击流混合器的流场具有混沌特性，因此可以得出不同操作条件下撞击流混合器具有相同的流场特性和运动趋势，验证了改变单一操作条件进行对比实验的合理性。

在图13(a)关联维随喷嘴进口雷诺数变化的3条曲线中，位于最上方的曲线对应的操作工况为Re=8470，其次为Re=7260，最下方的曲线对应为Re=6050。

再观察图13(b)和图13(c)可发现，Kolmogorov 熵和最大 Lyapunov 指数中3 条曲线的排列位置与关联维中的排列位置基本一致，除了个别点的值有所跳跃，这是由于撞击区流体的复杂性和不稳定性造成的，但并不影响3 条曲线的整体排列趋势。

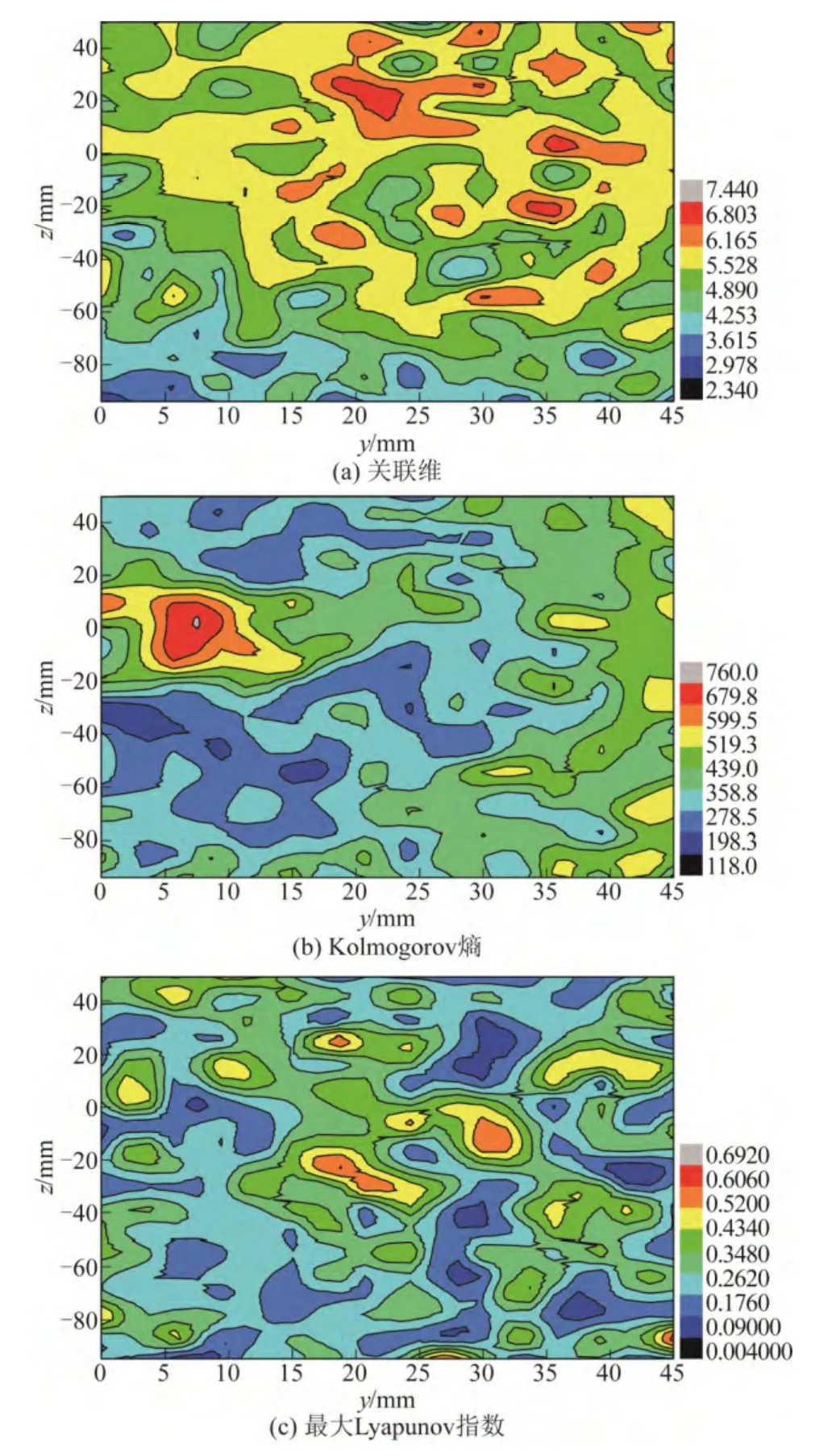
图12 雷诺数Re=6050 时撞击面的混沌特征参数

通过上述现象可以得出，在喷嘴直径和喷嘴间距保持不变的工况下，3 个混沌特征参数（关联维、Kolmogorov 熵和最大 Lyapunov 指数）随着单一变量喷嘴进口处雷诺数的增加，其数值具有相同的变化规律，均逐渐增大，撞击流混合器的微观混合效果逐步增强。这是因为流体初始速度的增大提高了流场的复杂程度和湍流动能，导致两股流体在进行撞击混合时，初始信息损失速率增大，彼此达到更好的碰撞、扰动，进行信息互换至最终混合。

3 结 论

图13 不同雷诺数下混沌特征参数的变化趋势

（1）采用湍流理论和混沌理论对浸没撞击流混 合器内速度信号进行分析，得到流场的关联维值均在2.32～7.52，流场具有自相似结构且存在分形。并且其Kolmogorov 熵和最大Lyapunov 指数均大于零，因此得出该双喷对置撞击流混合器速度场具有混沌特性。

（2）喷嘴间距较大时，撞击速度较小，撞击较不剧烈，而喷嘴间距较小时撞击不够完全，喷嘴进口处雷诺数和喷嘴直径保持不变时，湍流特性参数和混沌特性参数均随着的喷嘴间距增大现增加后减小，可以得到利于混合的喷嘴间距L=3d。

（3）由于进口处雷诺数的增加，流体初始速度的增大提高了流场的复杂程度和湍流动能，喷嘴间距和喷嘴直径保持不变时，湍流特性参数和混沌特性参数均随着喷嘴进口处雷诺数的增加而成递增趋势，雷诺准数有助于提高撞击流混合器的微观混合效果。

符 号 说 明

D—— 分形维数

不久，竹韵悠悠醒来了，脸色惨白地对龙斌笑了笑，站起来走到电脑前，在百度搜索键上打下了杂志文章的标题，一搜索又令她气愤难当，不但这篇文章上了网，而且点击率，跟贴率极高。许多不明真相的网友大骂竹韵是骚货，是祸水，要将她拉出去斩立决，什么难听的话都有。竹韵突然觉得自己掉进了一个污水池里，淹得快要窒息了……

d—— 喷嘴直径，mm

Ia—— a 方向湍流强度

k—— 湍动能，m2/s2

L—— 喷嘴间距，mm

m—— 嵌入维

N—— 测量次数

Re—— 雷诺数

u—— 时均总速度，m/s

uai—— 第i 次的该点a 方向瞬时速度，m/s

λ—— 最大 Lyapunov 指数

τ—— 延迟时间，s

[1] Elprein I T. Heat and mass transfer in opposing currents[J]. Engng. Physics，1961，6：62-68.

[2] 伍沅，陈煜. 撞击流反应制取“超细”白炭黑[J]. 化工学报，2003，54（10）：1381-1386.

[3] 伍沅. 撞击流——原理.性质.应用[M]. 北京：化学工业出版社，2006.

[4] 张建伟，伍沅，舒安庆，等. 浸没循环撞击流反应器的压力脉动特性[J]. 化工学报，2005，56（2）：266-269.

[5] 张建伟，焦丽. 撞击流反应器压力波动的多尺度多分形特征分析[J]. 化工学报，2006，57（7）：1558-1564.

[6] 林柯利，毕荣山，谭心舜. 利用面激光诱导荧光技术研究喷射器内液-液湍流混合特性[J]. 高校化学工程学报，2009，23（1）：28-33.

[7] 张建伟，殷婉君，孙熙同，等. 基于希尔伯特-黄变换的撞击流混合器浓度场特性分析[J]. 高校化学工程学报，2014，28（5）：971-978.

[8] Zhang Jianwei，Wang Xiangwang，Wang Chunyu. Multi-scale and multi-fractal characteristics of instantaneous velocity signals in impinging stream mixer[J]. The Canadian Journal of Chemical Engineering，2010，88（2）：172-178.

[9] 张建伟，宋艳芳. 撞击流反应器流场速度时间序列的结构复杂性分析[J]. 机械工程学报，2011，47（22）：174-180.

[10] 张建伟，马彦东，王显旺，等. 撞击流混合器内速度脉动的间歇性分析[J]. 实验流体力学，2012，26（2）：6-11.

[11] 毛德明，冯连芳，许国军，等. 用LDA研究搅拌釜内的流场[J]. 高校化学工程学报，1996，10（3）：258-263.

[12] 赵永龙，丁晶，邓育任. 混沌分析在水文预测中的应用与展望[J].水科学进展，1998，9（2）：181-186.

[13] 马军海，贾湖，盛昭瀚. 非线性经济时序的预测方法及其应用研究[J]. 管理科学学报，2001（4）：49-54.

[14] 何建华，杨宗凯，王殊. 基于混沌和神经网络的弱信号探测[J].电子学报，1998，26（10）：33-37.

[15] Packard N H ，Crutchfield J R，Farmer J D，et al. Geometry from a time series[J]. Rev. Letters，1980，45：712- 716.

[16] Grebogi C，Ott E，Yorke J A. Final state sensitivity：An obstruction to predictability[J]. Pys. Lett. A.，1983，99：415-419.

[17] Grassberger P，Procaccia I. Characterization of strange attracors[J]. Phys. Rev. Lett.，1983，50：346-349.

[18] Grassberger P，Procaccia I. Estimation of the Kolmogorov entropy from a chaotic signal[J]. Phys. Rev. A，1983，28：2591-2593.

[19] Renyi A. Probability Theory[M]. Appendix. Amsterdam ：North Holl and Press，1970.

[20] Wolf A，Swift J B，Swinney H L，et al. Determining Lyapunov exponents from a series[J]. Physical D，1985，16：285-317.

[21] Fraser A M，Swinney H L. Independent coordinates for strange attractors form mutual information[J]. Phys. Rev. A，1986，33（2）：1134-1140. 赵贵兵，石炎福，段文锋，等. 从混沌时间序列同时计算关联维和Kolmogorov熵[J].计算物理，1999，16（3）：309-315.