基于向量线性组合的并行矩阵乘法研究

郑建华，沈玉利，朱蓉

基于向量线性组合的并行矩阵乘法研究

郑建华，沈玉利，朱蓉

为了解决MapReduce框架下现有矩阵乘法算法性能不高的问题，提出了一种基于向量线性组合（Vector Linear Combination：VLC）的矩阵乘法处理模式，介绍了采用MapReduce框架实现基于VLC模式的矩阵乘法算法的过程，其中Map函数负责实现数据预处理，Reduce函数完成数乘操作和向量线性叠加。随后，讨论了影响算法执行时间的因素，并从理论方面比较了两种算法性能。实验结果显示，新算法所需执行时间更少，效率更高，与理论分析相吻合。

并行矩阵乘法；MapReduce；线性组合

0 引言

矩阵乘法应用广泛，传统串行矩阵乘法算法需要占用较多工作单元和较大存储空间，其时间复杂度一般为随着n值的增大，计算效率将受到很大的影响[1]。随着科学技术的发展，并行计算机的出现使大规模地提高矩阵运算速度成为可能，为了实现并行计算，需要将矩阵进行预划分，然后指派给不同的处理器。常用的矩阵分块乘法运算都是将矩阵分块再用递归算法进行计算，比较著名的分块矩阵乘法算法有Cannon[2]算法，Fox[3]算法，DNS算法，但是采用这些算法实现较为复杂，它们要求处理器个数P和矩阵的规模n之间存在关系而且单台计算机价格较为昂贵。

在大数据时代，随着MapReduce[4]成为最广泛用于处理数据密集计算的并行计算框架，许多研究者开始将MapReduce用于矩阵乘法[5-9]。其中文献[10]关注多个矩阵乘法，并提出一种将乘法转换为表连接的计算模式。其他文献[11,12]重点关注两个矩阵的乘法，但是他们主要是采用块级乘法模式（Block-level Multiplication：BLM）（注：本文命名的BLM与传统的分块矩阵乘法不是同一个概念），即用左矩阵A的一个行向量乘以右矩阵B的一个列向量得到目标矩阵C的一个元素。对于这种模式，在采用MapReduce计算框架计算时，存在两点不足，第一点当矩阵规模变大时，计算性能急剧下降，所耗费的计算时间急剧上升。其次，如果A为稀疏矩阵，采用BLM模式会导致大量无意义乘法运算。

在MapReduce计算框架中，每个MapReduce计算任务过程被分为两个阶段：Map阶段和Reduce阶段，每个阶段都是用键值对（key/value）作为输入（Input）和输出（Output）。其中Map阶段输出的键值对经过分区、排序和融合后作为Reduce阶段的输入。当采用BLM模式在MapReduce框架中实现矩阵乘法时，为得到矩阵C的一个元素，Map阶段为矩阵A和矩阵B的每个元素都产生一个键值对，然后在Reduce阶段先组合成一个行向量和一个列向量，再执行两个向量乘法计算，从而得到矩阵C的一个元素。这种模式的设计过程使得Map阶段产生太多的键值对，并存入Hadoop分布式文件系统HDFS[4]中，由于Reduce阶段需要从HDFS上读取Map的输出，导致系统I/O时间增加[13]，从而影响整个计算性能。

为解决BLM模式在MapReduce框架中出现的问题，本文提出采用向量线性组合的模式实现矩阵乘法，拟主要通过减少Map阶段输出的中间键值对来提高计算性能。

1 向量线性组合的矩阵乘法原理

图 1所示：

图 1 VLC计算模式原理示意图

本文称这种计算模式为VLC（Vector Linear Combination）模式。

则在VLC模式中，矩阵C的计算过程表述如下：

最终得到矩阵C公式（3）：

用MapReduce框架实现基于VLC的矩阵乘法时，Map函数主要负责矩阵A和矩阵B数据预处理工作，即将矩阵A拆分成单个元素，而矩阵B拆分成k个行向量，这种拆分方式将减少临时中间输出键值对。而Reduce函数主要通过数乘到中间权重向量，并对中间权重向量进行线性组合叠加得到矩阵C，当矩阵A为稀疏矩阵的时候，即如果aip为零，则Vijw也是一个零向量，不需要进行乘法计算，从而节省了计算时间，因此VLC模式也同样适合稀疏矩阵的乘法，故采用VLC模式可以有效的避免BLM模式中两大不足。

2 MapReduce框架下基于VLC模式的算法设计

根据MapReduce计算框架要求，编写基于MapReduce计算框架的算法关键是要实现Map阶段函数和Reduce阶段函数，为此本小节主要阐述这两个函数的实现过程。

本研究中将采用一个MapReduce工作任务（Job）完成整个基于VLC的矩阵并行乘法计算，Map函数负责接收矩阵输入，并根据VLC模式要求产生相应的中间输出键值对，而Reduce函数则对Map函数产生的中间键值对执行数乘操作，然后进行向量线性组合叠加，最后输出结果矩阵C。Map和Reduce函数的输入输出如

所示：

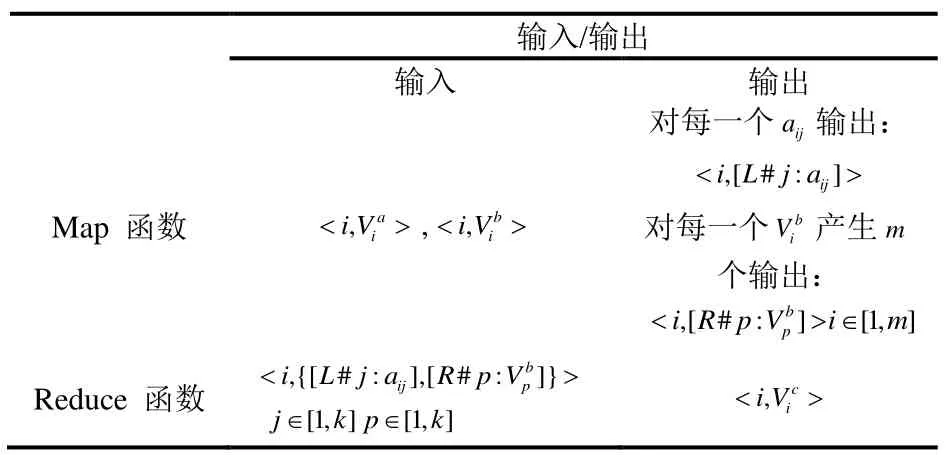
表1 Map和Reduce函数的输入输出

在MapReduce框架中，MapReduce框架会收集Map函数抛出的结果，并且把具有相同的键的键值对分组、排序，而Reduce函数接受MapReduce库分过组的(key,value[]),然后对具有相同键的中间结果集进行规约及相关处理，最后结果返回给MapReduce库。

因此在本文中，Reduce函数将接受矩阵行下标相同的键值对，这些数据即为计算矩阵C行向量的全部数据。Reduce函数将根据将复合数据中的区分矩阵A和B，并对满足条件复合数据中值进行数乘操作，即这个数乘结果即为中间权重向量，最后对同一个结点的Reduce函数的所有中间权重向量进行向量线性组合叠加即得到矩阵C的行向量这也是Reduce函数的输出。

基于以上分析Map函数实现过程伪代码描述如下：

Algorithm of Map Function：

Output：输出两种类型键-值序列对：○1 左矩阵输出其中键为i，是元素的行号，值为○2右矩阵输出：其中键为p,值为对。矩阵B的输出则与矩阵A不同，将针对矩阵B的每一

Procedure:

Begin

1: IF 输入矩阵是左矩阵

5: ELSE

6: 不输出任何键值对

7: END IF

8: END FOR

9: ELSE IF 输入矩阵是右矩阵

10: FOR p=1 to m DO BEGIN

12: END FOR

13: END IF

End

类似的Reduce函数实现过程伪代码描述如下：

Algorithm of Reduce Function：

Input：每个node得到输入数据是具有相同键值的一系列键值序列对：

3 算法分析

3.1 理论分析

计算时间是衡量矩阵乘法算法是否优越性的一个重要指标，特别是随着矩阵的增大，一般计算时间会快速地增加。对MapReduce计算框架而言，时间开销包括I/O耗时和CPU耗时，其中I/O开销包括从HDFS和本地硬盘读/写时间，而CPU开销包括执行 Mapper/Reducer/Combiner的时间和进行中间数据的分区、排序和融合所耗费的时间[13]。故减少中间键值对的数量将有助于提高整个算法计算性能。

文献[7]描述了一个典型的基于BLM模式的矩阵乘法，本文称该算法为BLMA算法。另外命名本文提出的基于VLC的矩阵并行乘法为VLCA算法，为了比较方便，假定A和B矩阵均为N阶方阵。

本文主要考虑两个影响计算性能的因素，第一个是Map函数所产生的中间键值对，第二个因素是元素被转移的次数。

在BLMA中，为计算矩阵C中的一个元素，需要左矩阵A的一个行向量和右矩阵B的一个列向量，因此对矩阵A和矩阵B的每个元素，Map函数要输出个中间键值，因此一共产生了键值对。而在VLCA中，Map函数产生的中间键值对为?个，而右矩阵输出个（参考第2小节）。如表2所示：

表2 两种影响因素比较

基于以上分析，我们定义理论计算性能如公式（4）、（5）：

基于以上分析，我们得到的理论性能对比曲线如图2所示：

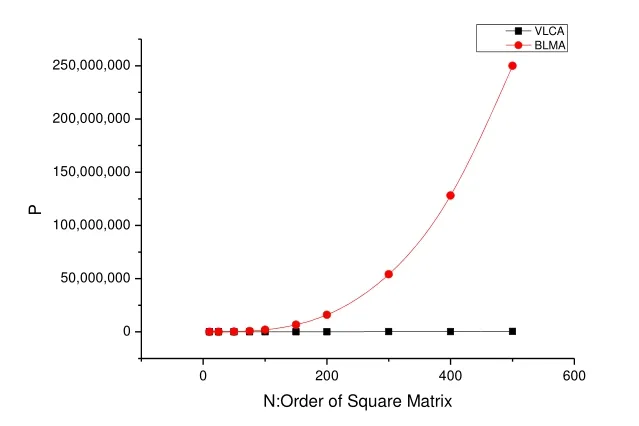
图2 理论性能比较曲线

图中显示当n逐渐增加的时候，两种算法的差距越来越大，表明了VLCA算法的优越性。

3.2 实验结果

不同的矩阵存储格式会产生不同的预处理开销，为了得到准确的实验比较结果，本次实验中对两种算法采用相同的输入格式，如图3所示：

图3 矩阵格式

实验中采用随机的方式生成不同大小的矩阵。

本次实验采用3台计算机构成的Hadoop集群，每台机CPU为2.13GHz，操作系统采用Ubuntu，Hadoop版本为1.0.4。为了获取最原始的计算性能数据，本集群并未做任何的配置优化。

不同类型矩阵的VLCA计算时间如图4所示：

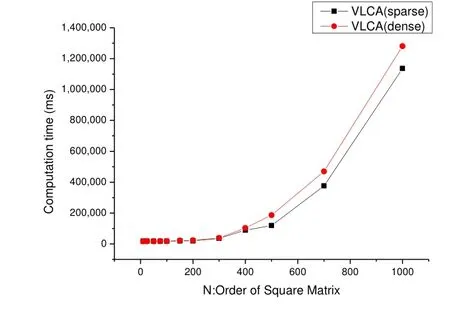
图4 不同类型的矩阵的VLCA计算时间

dense表示稠密矩阵，sparse表示稀疏矩阵，当n从0增加到1000，用于稠密矩阵的计算时间一直大于用于计算稀疏矩阵的计算时间，并且呈扩大趋势，这表明了该算法在计算稀疏矩阵时能节省计算时间。

BLMA算法和VLCA算法的计算时间比较如图5所示：

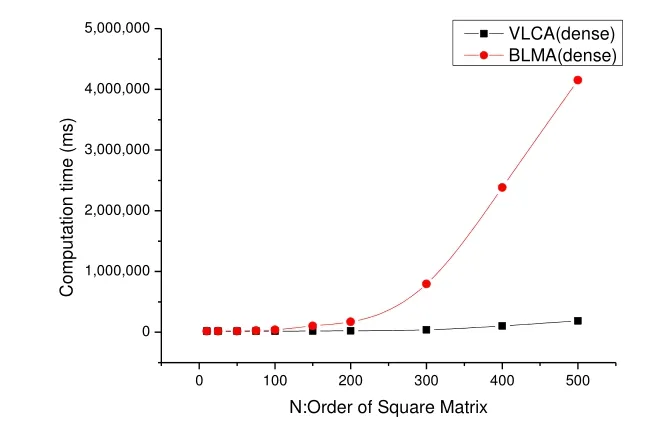
图5 两种算法的计算时间比较

当n <200的局部视图如图6所示：

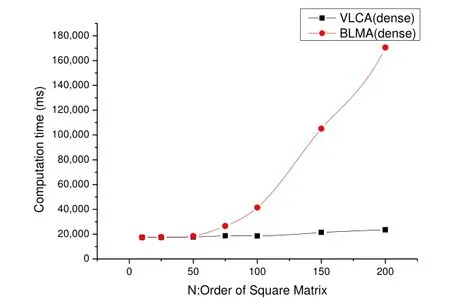
图6 两种算法的计算时间比较(n<=200)

图6中清晰表明两种算法的执行时间差距随着n的增加而增加，VLCA算法显示了较为优越的性能。而当n小于50，二者的执行时间基本相等，这是因为此时的计算量不饱和，整个任务的执行时间主要是启动MapReduce工作任务的时间。

3.3 分析结果通过对比理论分析和实验结果，可以得到3个结论：1）当矩阵比较小时，BLMA与VLCA性能相当，而当矩阵比较大时，VLCA显示出较优越的性能。

2）对比图2和图5发现，当n 为500，实验结果的时间耗比倍数（VLCA算法时间/BLMA算法时间）比理论分析的时间耗比倍数要小，这说明a不应该是0.5，应该是更大，可达0.9。说明基于MapReduce框架的并行算法中Map函数输出的中间键值多少是影响算法性能的最重要z因素。

3）VLCA用于稀疏矩阵并没有体现较大的性能优势，这进一步证明了第二个结论的正确性，即MapReduce框架处理中间键值对的时间要远比执行乘法运算耗费的时间多。

4 总结

面对越来越大规模的数据集，传统的矩阵并行算法并不适用，而MapReduce框架显示出了较好性能优势。当传统的基于MapReduce的BLMA矩阵乘法由于产生的中间键值对过多导致算法性能较低，为此本文提出了基于向量线性组合叠加的方式实现MapReduce框架下矩阵乘法，该方法极大地减少了中间数据的产生，实验结果表明算法性能得到提高。在后续的研究中将进一步优化算法，以提升对稀疏矩阵的算法性能。

[1] 雷澜. 矩阵乘法的并行计算及可扩展性分析 [J]. 重庆工商大学学报(自然科学版), 2004, 21(02): 121-123.

[2] Cannon L E. A cellular computer implement the Kalman filter algorithm [D]. Bozeman US: Montana State University, 1969.

[3] Fox G C, Otto S W, HEY A J G. Matrix algorithm on a hypercube I:matrix multiplication [J]. Parallel computing, 1987, 4(1): 17-31.

[4] Dean J, Ghemawat S. MapReduce: a flexible data processing tool [J]. Communications of the ACM, 2010, 53(1): 72-77.

[5] Huang B, Wu Y. Matrix multiplication in MapReduce [EB/OL].https://www.cs.duke.edu/courses/cps216/current/ Project/Project/projects/Matrix_Multiply/proj_report.pdf,2 013,02.

[6] Norstad John. A MapReduce algorithm for matrix multiplication [EB/OL].http://www.norstad.org/matrixmultiply/,2013,02.

[7] Rajaraman A, Ullman J D. Mining of massive datasets [M]. Cambridge: Cambridge University Press, 2011.

[8] Seo S, Yoon E J, Kim J, et al. HAMA: an efficient matrix computation with the MapReduce framework[C]// Proceedings of the 2010 IEEE Second International Conference on Cloud Computing Technology and Science.Washington:IEEE Computer Society, 2010:721-726;

[9] Zhang J. Implementation for large scale matrix multiplication on mapreduce parallel framework [J]. Computer Applications and Software, 2012, 29(6):267-71.

[10] J. Myung,S. G. Lee.Matrix chain multiplication via multi-way join algorithms in MapReduce [C]//Proceedings of the 6th International Conference on Ubiquitous Information and Communication. 2012:53-58.

[11] Zeng D J. Large matrix multiplication processing program design of cloud platform [J]. Science Mosaic, 2012, 24(5): 42-45.

[12] Z. G. Sun, T. Li,N. Rishe. Large-scale matrix factorization using MapReduce[C]//Proceedings of the IEEE International Conference on Data Mining Workshops. Washington:IEEE Computer Society, 2010:1242-1248

[13] Dawei Jiang, Beng Chin, Ooi Lei, et al.The Performance of MapReduce: An In-depth Study[J].Proceedings of the VLDB Endowment 2010,3(1):472-483.

TP312

A

2015.04.16）

1007-757X (2015)07-0005-03

广东省科技计划项目（2012B040500040）；广东省科技计划高新技术产业化项目（2012B010100048）；广州市海珠区科技计划项目（2014-cg-31）

郑建华（1977-），男，汉族，湖南嘉禾，仲恺农业工程学院，讲师，博士，研究方向：系统架构设计，云计算，大数据处理与挖掘，广州，510225

沈玉利（1955-），男，汉族，山东费县，仲恺农业工程学院，教授，博士，研究方向：模式识别与智能处理，大数据处理与挖掘，广州，510225

朱蓉（1976.9-），女，汉族，江西吉安，仲恺农业工程学院，讲师，硕士，研究方向：系统架构设计，云计算，大数据处理与挖掘，广州，510225