XML数据公交信息查询优化算法及实现

刘明珠++丁亦楠++郑云非

摘要：针对公交线路规划的问题，必须提供一个准确快捷的公交查询系统以满足人们日常出行的需求.研究了基于XML数据的公交查询系统，该系统采用B/S模式，利用ASP.NET框架和C#语言，实现了公交运行查询功能.在换乘查询算法部分及在Dijkstra算法的基础上，分析了路径寻优的原理，实现了路径距离计算的具体方法.并通过减少临时节点排序及数量的方式，改进了Dijk-stra算法，最终减少了寻找路径的时间并简化了路径计算，最后，以天津市公交数据为例.用改进的Dijkstra算法对公交查询系统进行了分析验证，结果表明，利用改进的Dijkstra算法可以实现高效的公交信息查询，节约查询时间，节省内存资源.

关键词：公交查询；Dijkstra算法；XML数据；路径寻优；最短路径

DOI： 10.15938/j.jhust.2015.02.016

中图分类号：TP319

文献标志码：A

文章编号：1007-2683（2015）02-0085-06

0 引 言

随着现代城市规模发展，城市的公交线路也越来越复杂，准确又方便地查阅公交线路，已经成为与人们生活息息相关的问题.传统的公交查询系统大多使用Sybase SQL Server、Oracle等传统数据库系统保存公交信息数据，并运用（structured querylanguage SQL）语言实现对这些数据库的操作.SQL语法简单，语言语句可嵌套，这使它具有极大的灵活性，但是，对于管理者的要求较高.目前，利用XML文件的结构化标记数据和可移植性的特点，构建公交查询系统后台数据结构，以减轻系统管理者负担，并提供准确、快捷的公交线路查询系统成为智能公交系统的研究热点之一.XML即可扩展标记语言，它使用表示起始和结束标签的语法来描述和交换独立于应用程序的结构化数据.使用XML存储数据使得管理者不再需要使用传统的soL语言来更新管理数据，减轻了管理人员的负担.本文首先对Dijkstra算法进行改进，并在Visual Studio开发环境下，利用ASP.net框架，采用B/S模式，构建XML数据，并将线路与站点数据相结合，同时融合拐点数据，使得线路查询算法更加简单，为公交查询系统的数据管理提供了一种新方法.

1 系统需求描述

1.1 性能需求

一个好的公交查询系统应具有准确性，快速性，易扩展性和易使用性.它保证系统输出结果的准确性，避免出现重复或者错误的查询结果给用户造成误导，并且在数据的导入、导出和查询过程中数据的处理时间响应上不超过ls.系统利用的XML数据非常便于管理者在后台随时进行更新和修改，即可直接打开XML数据文件进行手动修改.同时查询者无需进行登录即可进行公交查询，系统配备合理的人机交互界面，方便用户查询和使用，节约了用户查询时间.

1.2 功能需求

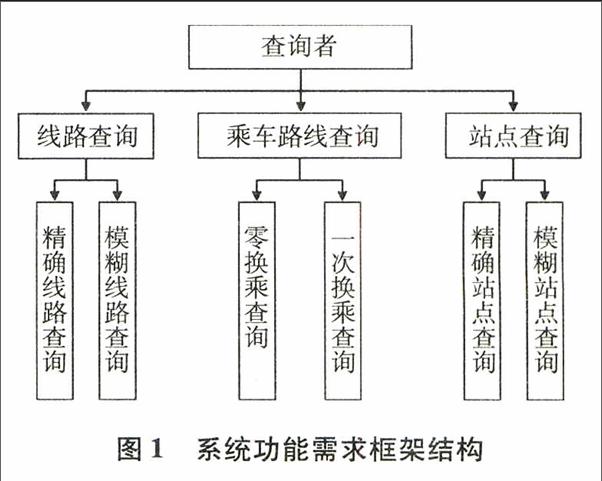
公交查询系统功能需求结构如图1所示.

1）线路查询：包含了线路的上、下行信息，并涵盖了线路经过的所有站点信息.当用户输入的信息不明确或不详细时，系统自动进行模糊查询，为用户匹配需要的线路信息.

2）站点查询：此功能在用户进行查询时，将包含此站点的所有公交线路反馈给用户，若用户输入的站名不明确时，系统自动进行模糊查询，为用户反馈合适的公交线路信息.

3）乘车路线查询：本系统以较少换乘次数作为设计依据设计了零换乘站点查询和一次换乘查询.首先输出零换乘的查询结果，其次输出一次换乘的查询结果，给查询者带来方便.

2 Dijkstra换乘算法描述及其优化

Dijkstra算法以广度优先算法为基础，主要解决从固定的单个点源，经过若干点后，到其他固定顶点的最短路径问题.本系统换乘查询部分采用了改进的Dijkstra换乘算法.

2. 1 基于传统Dijkstra算法的换乘查询算法

在本文设计的公交查询系统中，一次换乘查询采用了Dijkstra算法，具体过程如下：

Stepl.设起点为站点A，设终点为站点C，其它的站点为站点B.设从站点A到站点B的集合为U（A，B）距离为AA，若站点B为中转站，则设AA=0；若站点B非中转站则AA=∞.

Step2.计算出AA的具体数值，对AA的值排序，并从AA最小值开始暂定其为AA的值，暂定该AA下的站点B为最佳中转站点.

Step3.设从站点B到站点C的集合为U（B，C），距离为AB，则从站点A到站点C的距离为AC=AA+AB.对AC的值和对应的换乘数据进行保存.

Step4.重复step2和step3直到所有AA为最大值.

Step5.对所有已保存的AC的值进行排序找到从站点A到站点C的最短距离和相对应的换乘数据，

该过程基于传统Dijkstra算法可以实现一次换乘查询，提供准确结果.但由于遍历计算节点较多，并产生大量中问数据，导致其效率不高，算法时问得不到优化.

2.2传统Dijkstra换乘算法优化原理

基于传统的Dijkstra换乘算法，对于一个公交查询系统，一般来说有以下两种常规优化方案：

1）传统优化方案一：该Dijkstra算法优化方案根据在查询中转站时，对中转站设置一定的权值来实现，这样做的好处是可以对换乘的次数进行排序，优先选择少换乘的路线，之后再对换乘路线的距离进行计算并排序.但是，这种方案当换乘次数增多时，会产生大量的查询线路无用结果，并且由于权值的加入，最终导致运算结点的增加，使得运算次数增多，不具备一定的实用性，虽然针对于传统的Dijk-stra算法进行工一定优化，但并不是最佳优化方案.

2）传统优化方案二：该Dijkstra算法优化方案在计算起点A到中转站B的距离AA时只计算站点B为中转站的距离，然后直接计算站点B到站点C的距离AB，最后依据AC=AA+AB直接计算全程线路的距离AC的值后再对AC排序.这样做减少了中途排序的过程，节约了大量计算机内存.但是这种方案在查找同一组线路下的中转站会出现中转站重复的情况，进而增加中途结点，没有实现算法完全优化.

2.3 本系统Dijkstra换乘算法优化原理

在本系统中，传统的Dijkstra算法在计算过程中产生大量的0元素，∞元素以及中间数据，这样做会占用较多计算资源，且该算法的时间复杂度为O（n2），当数据量过大时，中途的结点数据量会占据大量的计算机内存单元，算法运行的时间将会不可接受，因此，需要对传统的Dijkstra换乘算法进行优化，使之减少资源占用，减轻计算复杂度，优化实现的具体过程为：

Stcpl.设起点为站点A，终点为站点C.找出包含A的线路L（A）和包含站点C的线路/（C）.

Step2.分别求出线路/（A）和线路L（C）的所有站点，找出L（A）与L（C）线路站点中包含的相同站点，即为中转站点1.若查找出的相同站点包含重复的，L（A）与L（C）线路，则停止重复查找，直接查询下一条线路的相同站点.

Step3.直接计算站点B到站点C的距离AB.

Stcp4.依据AC=AA+△B直接计算AC的值，再对AC排序.

这样做与传统的Dijkstra算法过程相比，避免了巾途积累大量的结点数据，并减少了中途排序的过程，当算法在运算过程中产生n个结点数时，优化算法的时间复杂度减少为0（n）这样节约了大量计算机内存并节省了大量运算时间，并提高了查询速度.

2.4 Dijkstra换乘算法优化实验验证结果

为了验证本系统的Dijkstra换乘算法优化的搜索效率，正确性以及优化效率，本文对传统Dijkstra算法，传统Dijkstra算法优化方案一，优化方案二和本系统的Dijkstra优化算法分别进行了实验，并进行了算法的对比验证.

在进行实验验证时，首先选取10组不同的起点和终点数据，然后使用这10组数据进行线路查询，在换乘线路查找过程中，分别记录使用这4种算法方案所产生的平均节点数及算法的搜索效率，并验证输出结果的正确性，最终分析说明优化Dijkstra换乘算法相比其它3种算法方案的提升效率，各项比较结果如表1所示，

从表l中可以看出，使用优化后的Dijkstra换乘算法过程中产生的节点数明显减少，并且优化提升明显，相比其他3种算法方案，本系统使用的Dijk-stra优化换乘算法很好的节省了内存占用单元和查询时间，满足了用户需求.

3 基于XML数据的公交信息查询优化算法的实现

3.1 XML数据模块设计说明及程序实现

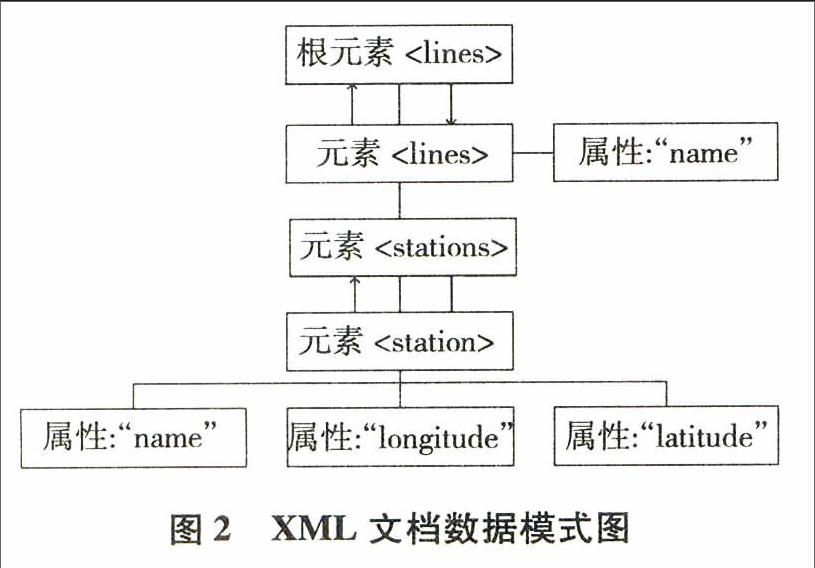
XML数据设计直接影响系统的性能以及管理员的维护.XML数据将线路与站点数据相结合，并且融合了线路拐点数据，所谓拐点即公交按其线路行走时需要拐弯的点，融合拐点数据后，使站点距离计算更加精确，本系统的XMI。数据模块如下所示：

由于XML文档可以被表示为标签在节点上的树，则通过图2表示出该XML文档的数据模式图.通过这些数据可以查询乘车线路，并计算出两站点之间的距离，并且非常便于管理员在后台随时更新和维护该XML数据.

在此模块中：

主要包含3个元素，分别为：station元素、line元素及lines元素.

1）标签中存储了该条线路的所有站点和拐点.其中，元素name表示站点名称，若该点为拐点，则name为空，元素longitude表示该站点（拐点）的经度，元素latitude表示该站点（拐点）的纬度，用C#进行数据传人时，首先建立XS-pot类，类中定义了用来存储线路名称的字符串变量和用来存储坐标的坐标变量，用XSpot类定一个spot自定义类型，将每条线路的站点数据分别存人其中.

2）标签中存储了一条线路和该线路所包含的所有站点和拐点，其中，元素name表示线路名称.

3）标签中存储着所有线路，在用C#进行数据传人时，首先建立XLine类，类中定义了用来存储线路名称的字符串变量和用来存储线路包含的站名名称及站点信息的XSpot变量.用XSpot类定义一个spots自定义类型，将spot内的每条线路站点信息全部存人其中，整合为全部线路的全部站点名称，并用XLine类定义一个line自定义类型，将标签内的数据全部存人line中，其中包含每条线路名称name和对应的站点及站点坐标spots.

3.2计算站点距离的数学模型描述

1）当用户从站点A1到站点AM时，中途要经过m-2个站点及拐点，分别设站点为A2，A3，…，Am-2，A—1·

2）设站点A1的经度为x1，，站点A1纬度为y1；站点A2经度为X2，站点A2纬度为Y2，则站点A1与站点A2的经度差为

X1= X2 -Xl，

（1）

它们的纬度差为

3）由于地面上经度或纬度相差1度以内对应的地表弧长大约是S =lllkm，且站点与站点间的距离都小于1经度或l纬度.因此，站点A.与站点A2之间的距离为

同理，站点A2与站点A3之间的距离为

站点Am一，与站点Am之间的距离为

4）由此可知，从站点A1到站点Am，即用户的乘车所经过的距离为

3.3基于优化Dijkstra乘车查询算法的实现

本系统乘车查询实现分为零换乘与一次换乘两部分.

3. 3.1零换乘

首先应用C#的List容器类以及System.Xml控件将XML后台数据中的线路信息与站点拐点的信息传人程序中，并使用List类构建linesl和lines2两个新容器，设用户查询的起点站为stationl，终点站为station2，查找包含stationl的所有线路并将其存入容器linesl中，同时将包含station2的所有线路存入lines2中.之后，使用List类构建line容器来保存共同包含stationl与station2的线路，此线路即为用户零换乘所需要的乘车线路，之后利用站点距离数学模型及C#语言实现可计算出stationl到sta-tion2的距离.在C#中，求两个List的交集，可以通过调用List类中的Intersect方法”line=linesl.Inter-sect（lines2）. ToList（）”；利用C#容器类的这个特点可简单有效的求出用户所需的乘车线路，再通过索引找出stationl及station2分别在line中的位置，即可求出用户乘坐该线路所要经过的站点及距离.最后，利用C#语言提供的接口IComparer，建立内部继承类，并利用该接口中提供的CompareTo（）函数对类中的成员进行比较，通过这个方法，对line中的线路路径长度进行比较后排序并将结果存人新容器lines中，可得出零换乘从路径最短到路径最长的查询结果（流程图如图3左边所示）.

3.3.2 一次换乘

用C#语言实现时，首先设起点站为stationl，终点站为station2，利用Find（）函数，找出所有包含stationl的线路liriel中以及所有包含station2的线路line2，并用索引标记出stationl，station2分别在lineI和line2中的位置.其次，利用判断中转站的方法”Linel.spots[i].GetName（）==line2.spots[j].GetName（）”来找出line1和line2中的共同站点，即换乘站点，其中，spots代表线路的站点，GetName（）用来获取站点中的线路名称.由于在相同linel与line2问一般会有多个换乘站点，因此，先通过对sta-tionl与station2到换乘站点距离分别进行计算，求出station1到station2的距离，再取出stationl到sta-Lion2存相同line1与line2下的最短距离，最终只保留相同linel，line2下stationl到station2的最短路径结果，并保存在List容器path中，再进行下一组line1，line2的判断.最终，将保留的换乘查询结果排序并利用lines.Add（path）；全部保存在List容器liries中，即为一次换乘的乘车线路（流程如图3右边所示）.

3.4查询结果的输出

本系统通过使用天津市公交信息数据，最终实现了线路查询、站点查询、乘车线路查询三大功能.

1）线路查询：在该方面本系统以“101路”线路作为实验数据，在进行线路查询时，输入“101”，通过模糊查询来找到101路公交的上下行线路所有信息，查询结果如图4所示.

2）站点查询：在站点查询的方面，本系统以“天津站”为例，查询了经过天津火车站的所有公交线路，查询结果如图5所示.

3）乘车路线查询：在乘车路线查询结果输出方面，系统根据人们出行时的乘车心理，首先选择了输出零换乘的查询结果，当零换乘的查询结果较少或没有零换乘的乘车路线时，系统将继续自动进行一次换乘查询，并将结果输出.同时，为了保证系统结果简明扼要，在进行线路查找时，添加了限制语句，令输出的乘车线路结果保持在5条以内，既当容器lines中存储的线路个数达到5条时，系统自动停止线路查询，这样既减少了搜索乘车线路所花费的时间，又给用户提供了快捷方便的结果.系统以起点为“天津站”，终点为“天津西站”作为实验依据，对该系统进行了实验验证，乘车线路的查询结果如图6所示.

4 结 语

本系统首先通过使用XML数据，进而实现对传统Dijkstra换乘算法的改进，并将结果与传统Dijk-stra换乘算法和传统Dijkstra换乘优化方案进行比较，验证了本系统算法的优越性，最终构建了一个对于用户方便使用，对于管理员方便管理的简便实用的公交查询系统，实验表明了利用改进的Dijkstra算法可以实现高效的公交信息查询，节约了查询时间，节省了内存资源.该系统对于传统Dijkstra换乘算法的优化为公交查询系统提供了一种新的解决思路.