求所有最小点成本最短路径算法

何建军　王丽芳

摘要摘要：对点带成本的最短路径问题进行了研究。根据点带成本最短路径问题特点，对Dijkstra算法进行修改后给出一个时间复杂度为O（|V|2+|E|）、空间复杂度为O（|V|+|E|）的算法，并在此基础上充分利用问题的特点，给出一个时间复杂度为O（w|V|）、空间复杂度为O（|V|+|E|）、构造所有点带成本最短路径的算法。

关键词关键词：最短路径；点带成本；带权图；最小点成本最短路径

DOIDOI：10.11907/rjdk.1431088

中图分类号：TP312

文献标识码：A文章编号文章编号：16727800（2015）004007803

0引言

最短路径（SP）问题一直是运筹学、计算机科学、交通运输等领域的研究热点。很多实际问题都可以转化为网络中的最短路径问题，如道路交通网络中的出行路线选取问题、计算机网络中的路由选择问题等。针对网络的最短路径问题研究具有重要的理论和现实意义。早期专家学者研究的算法有Dijkstra算法[1]、Bellman算法[2]、Floyd算法等，现阶段对最短路径算法的研究呈现以下几个特点：①并行化，如文献[4][6]等；②将遗传算法、神经网络、启发式算法等引入最短路径算法设计中，如文献[7][9]等；③对各种约束条件下的最短路径算法进行研究，如文献[10][13]等；④研究最短路径算法的各种优化实现，如文献[14]。

早期文献[10]对点带成本约束的最短路径算法进行了研究，文献[10]首先证明了点带约束成本SP问题是一个NP完全问题，然后用动态规划法给出一个时间复杂度为O（Cmn）的伪多项式时间算法。对最小点成本最短路径问题，文献[10]把主要目标（路径长度最短）的最优解作为次要目标（点成本最小）的约束条件进行求解，需要两次调用Dijkstra算法求最短路径，并且需要构造网络G′=（V，A′，L′），造成一些不必要的时间和空间开销。本文对Dijkstra算法进行了改进，使其适合于求解最小点成本最短路问题，然后只调用一次修改后的Dijkstra算法，完成对最小点成本最短路问题的求解，在求解过程中不需要构造新的网络，本质上是一个贪心算法。

1问题描述

定义1：图G=（V，A，L）称为点带成本带权图，给它的每条边（vi、vj）∈A赋一个非负参数li，j，称作长度；给它的每一vi∈V赋一个正参数ci，称作点成本。点带成本带权图G中一个特殊点s称为源点。

定义2：设P是点带成本带权图中一条路径，记P=v1v2…vrvr+1，定义P的长度为L（P）=l1，2+l2，3+…+lr，r+1。定义P上的点成本为C（P）=a1+a2+…+ar。

定义3：点带约束成本的SP问题：求点带成本带权图中给定的两顶点间一条路径P，使得P在满足C（P）≤C的前提下，路径长度最短.这里C是一个正有理数。

定义4：最小点成本最短路径（MCSP）问题是从源点到其余各个顶点的所有最短路中求点成本最小的最短路径，即求：min{C（P）：P是v1→vn的最短路径}。定义5：设G=（V，A，L）是点带成本带权图，SV且源点s∈S，任意vi∈V-S，从s到vi除了vi以外其它顶点都属于S的路径，称为从s到vi的受S限制路径。把从s到vi的受S限制的所有路径中长度最短且在满足长度最短的条件下，点成本最小的路径称为s到vi的受S限制最小点成本最短路径。记s到vi的受S限制点成本最小最短路径的长度和点成本构成的二元组为（Li，Ci）i，简称LC二元组，其中Li为路径长度，Ci为点成本。

定义6：（Li，Ci）i<（Lj，Cj）j，当且仅当Li

显然集合{（Li，Ci）i|vi∈V-S}上的“≤”关系具有自反性、反对称性和传递性。又由于任意两个实数都可以比较大小，所以集合{（Li，Ci）i|vi∈V-S}和它上面的关系“≤”构成一个全序关系，总有最小元存在。

2算法基本思想

设P=sv2，…，vk，…，vL是图G的一条最小点成本最短路径，则P′=v1v2，…，vk是图G中从s到顶点vk的最小点成本最短路径，否则设P''=sv′2v′3…vk是从s到vk的最小点成本最短路。把路径P中顶点vk前面的部分用P''替换会得到一条可能比P更短或者与P长度相同、但点成本更小的路径，这些都与P是从v1到vL的最小点成本最短路径矛盾。这说明最小点成本最短路问题具有最优子结构性质，可以使用动态规划法或贪心法进行求解。

又由于{（Li，Ci）i|vi∈V-S}是有限全序集，最小元总是存在的，所以可以采用如下贪心策略：设置一个集合S，初始时S中仅含有源s，然后每次找到V-S中最小的（Li，Ci）i，将vi添加到S中，同时对数组（Lj，Cj）j按如下方式修改：（Lj，Cj）j=min{（Lj，Cj）j，（Lj，Cj）j+（li，j，aj）}，如果（vi，vj）∈E，这一过程直至S中包含所有V中顶点为止。同时若有（Lj，Cj）j=（Lj，Cj）j+（li，j，aj），其中（vi，vj）∈E，则vi 一定会出现在从s到vj的最小点成本最短路径上。可以利用LC数组的这一特性构造出所有点成本最小最短路径，这是文献[10]未给出的。

3算法描述

算法1：功能：计算LC数组。输入：图G的邻接表和各个边和点的权，源点s，图G顶点数n。输出：LC数组。

S={s}，（Ls，Cs）s=（0，as）；

for i：= 2 to n do（Li，Ci）i=（Ls，Cs）s+（ls，i，ai）；

for（i=1；i<=n-1；i++）；{从V-S中选取一个顶点vj，使其（Lj，Cj）j最小；将vj加入到S中；for vk∈（V-S）∩N（vk） do （Lk，Ck）k=min{（Lk，Ck）k，（lj，k，ak）} }算法2：功能：构造出所有的最小点成本最短路径。输入：LC数组，图G的邻接表，源点s， 图G顶点数n。输出：所有最小点成本最短路径。for（i=1；i<=n；i++）{对顶点vi 的所有邻接点vj计算：if（（Li，Ci）i=（Lj，Cj）j+（li，j，aj））{把vi放入栈Q中；Depth（Q，G，LC，vj）；把vi弹出栈Q中；}}Depth（Q，G，LC，vh）{if（vh==s）{输出s；自定向下输出Q中顶点，但不弹栈}else{对顶点vh的所有邻接点vj计算：if（（Lh，Ch）h=（Lj，Cj）j+（lh，j，aj）） {把vh放入栈Q中；Depth（Q，G，LC， vj）；把vh弹出栈Q中；}}}算法正确性证明：定理1：每次选择一个顶点放入S中并执行完更新操作后，得到新的、正确的LC二元组。证明：在算法初始化时，得到的LC数组显然是正确的。放入S的顶点vi，除了vi的邻接点外，其余顶点不会经过vi。vi的邻接点可能会经过vi，但已经对其LC进行了更新。所以，每次选择一个顶点放入S中并且执行完更新操作后，会得到新的、正确的LC二元组。

定理2：算法1能正确求出从源点到各个顶点的LC二元组。

证明：对放入S中的定点次序k进行归纳：

当k=1时，首先放入S的源点s，（Ls，Cs）s的Ls是从s到s最短路径长度，Cs是从s到s的长度最短的最小点权。

设当k≤h时，前h个放入S中的顶点，其相应的LC二元组分别是从s到该顶点的最短路径长度，及从s到该顶点的所有最短路径中的最小点权。

现在证明第h+1个放入S中的顶点vi，（Li，Ci）i的Li是从s到vi最短路径长度，Ci是从s到vi的长度最短的最小点权。设P是从s到vi长度最短、且在长度最短的前提下点权最小的路径。根据贪心选择策略，P必经过S外至少一个顶点才能到达vi，不妨将P从s出发，第一个经过S外的顶点为vx 。结合定理1，这时必然有（Lx，Cx）x<（Li，Ci）i。这与贪心选择策略矛盾。

算法1的正确性可以保障算法2是正确的。

4算法性能分析和实例

算法1：有一个二重循环，每重循环最多循环|V|次，在整个算法运行过程中最多访问每条边一次，所以其时间复杂度为O（|V|2+|E|）。设最小点成本最短路径的数目为w，则算法2的时间复杂度为O（w|V|）。算法1的空间消耗主要在邻接表存储和LC数组存储，其空间复杂度为O（|V|+|E|）。算法2的空间消耗主要在邻接表、LC数组、栈的存储和递归调用栈上，递归调用栈的深度最多为|V|，所以其空间复杂度为O（|V|+|E|）。

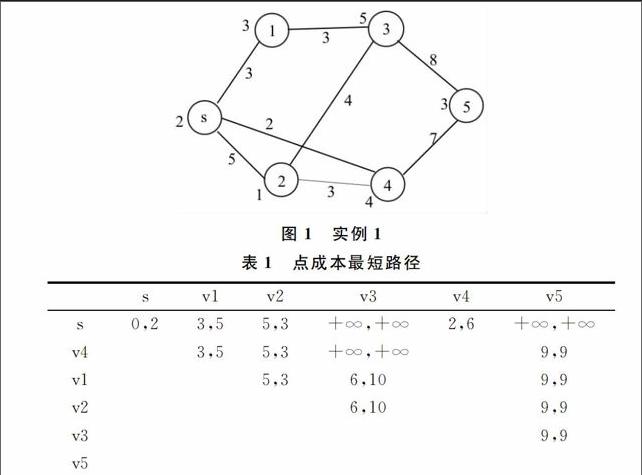
图1为一个点带成本带权图，用算法1和算法2求出从源点s到其余各个顶点的点成本最短路径，如表1。

5结语

本文在文献[10]的基础上对点带成本问题进行了研究，结合问题的特点给出了求所有点带成本最短路径算法。在点带成本最短路径问题中，把所有点的成本都设为1，则点带成本路径问题就变成了顶点数最少的路径问题。虽然本文给出了一个求解点带成本问题的多项式时间算法，但如果图中定点数过多，其二阶的时间消耗仍然是难以接受的。所以，下一步的研究方向是点带权最短路径问题的并行化算法和线性近似算法。

参考文献参考文献：

[1]DIJKSTRA E W.A note on two problems in connexion with graphs[J].Numerical Mathematics， 1959（1）：269271.

[2]BELLMAN R.On a routing problem[J].In Quarterly of Applied M athematics， 1958， 16（1）： 8790.

[3]DEON ，PANGCY.Shortest path algorithms：taxo no my and annotation[J].Networks，1984（14）： 275323.

[4]周益民，孙世新，田 玲.一种实用的所有点对之间最短路径并行算法[J].计算机应用，2005，25（12）：29212922.

[5]黄跃峰，钟耳顺.多核平台并行单源最短路径算法[J].计算机工程，2012，38（3）：13.

[6]卢照，师军.并行最短路径搜索算法的设计与实现[J].计算机工程与应用，2010，46（3）：6971.

[7]邹亮，徐建闽.基于遗传算法的动态网络中最短路径问题算法[J].计算机应用， 2005， 25（4）：742744.

[8]洪斌， 张红岭，王剑雄，等.求解多约束最短路径的改进ACNN算法[J].河北建筑工程学院学报，2013，31（3）：109112.

[9]戴树贵，潘荫荣，胡幼华，等.求带多个限制条件的单源多权最短路径算法[J].计算机应用与软件，2004，21（12）：7881.

[10]李帮义，何 勇，姚恩瑜.点带约束成本的最短路问题[J].高校应用数学学报，2000，15（1）：9396.

[11]郝光，张殿业，冯勋省.多目标最短路径模型及算法，2007，42（5）：641646.

[12]周经伦，吴唤群.受顶点数限制的最短路问题及其算法[J].系统工程，1996，14（5）：3744.

[13]FREDMAN M L， TARJAN R E.Fibonacci heaps and their uses in improved network optimization algorithms[J].ACM， 1987， 34（3）： 596615.

[14]CHERKASSKY B V， GOLDBERG A V， RADZIK T.Shortest path algorithms： theory and experimental evaluation[J].Mathematical Programming， 1996（73）：129174.

责任编辑（责任编辑：杜能钢）