星球车车轮的滑转率估计方法
尤+波++时+洋


摘 要:未来的勘探任务要求星球车自主运行于复杂的星球表面,车轮滑转率的有效估计是星球车高性能移动控制的关键,基于车辆地面力学理论,建立了基于滑转率的车轮一土壤相互作用力学积分模型,推导了积分模型中集中力的解析表达式.针对模型方程组的高度耦合性和复杂非线性,分析了模型参数间的耦合关系;结合被动滑转原理和参数关系分析结果,系统研究了星球车车轮的滑转率估计方法.通过开展轮壤相互作用试验,将车轮滑转率的模型计算值与试验所得值进行比较,验证了积分模型滑转率估计方法的正确性,
关键词:滑转率;地面力学;被动滑转;耦合关系
DOI: 10.15938/j.jhust.2015.02.005
中图分类号:V476.4
文献标志码:A
文章编号:1007-2683(2015)02-0023-05
0 引 言
同探索海洋、陆地和近地空间一样,人类对外部星球的探索本身就是对地球生命进化研究的重要一步.星球表而环境的复杂性与不确定性,使星球车在运行过程中极易发生滑转现象,对星球车移动系统方面研究提出了许多挑战.滑转率估计方法研究可以使人们更好了解车轮滑转状态,对星球车控制策略设计、路径规划研究以及驱动力驱动力学特性分析具有重要意义.
文提出利用根据星球车车辙痕迹检测车轮滑转率的方法,但该方法中车轮痕迹必须人工测量,无法实现自动检测;文通过视觉方法检测车辙的形状,经过数据转换实现滑转率的检测,但对于无轮刺的星球探测车车轮,该方法并不适用;应用地面力学解决星球车运动控制问题一直是该领域研究的热点与难点,文在忽略离去角的基础上,基于Wong-Reece的正应力分布模型和Janosi的塑性剪切特性模型推导了车轮集中力的封闭解析表达式,但对于星球车车轮滑转率的估计方法系统研究很少.
本文基于地面力学理论,建立车轮在被动滑转状态下的车轮一土壤相互作用力学积分模型,推导车轮挂钩牵引力和支持力的解析表达式,在分析模型参数耦合关系的基础上,提出星球车车轮滑转率估计方法,最后结合试验数据验证该方法的正确性.
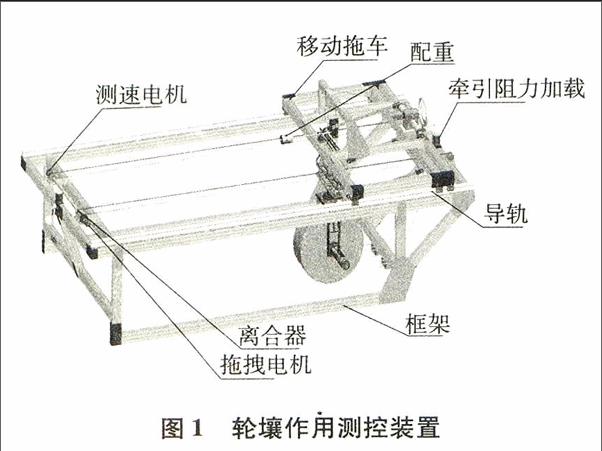
1 轮壤相互作用测控装置
车轮与土壤相互作用测控装置如图1所示,该装置包括前进电机、拖拽电机和转向电机3个伺服电机,具有离合器、配重、轮压加载机构、牵引阻力加载机构以及导轨等机械装置,安装了六维力/力矩传感器以及测速电机等感知器件.
在离合器断开的情况下,单独驱动车轮前进电机带动移动拖车在导轨上运动,可以开展车轮被动滑转试验.基于配重和轮压加载机构,可以设定稳定的车轮正压力;通过牵引阻力加载,可以设定恒定的车轮挂钩牵引阻力,车轮正压力和挂钩牵引阻力由六维力/力矩传感器进行测量,移动拖车的速度由测速电机转换获得,车轮滑转率通过拖车速度和车轮滚动角速度转换得到.图2为测试车轮模型.
2 基于滑转率的星球车轮壤相互作用建模
2.1滑转率定义
滑转率反映了车轮实际前进线速度和滚动速度之间的偏差程度,用式(1)进行定义:式中:r为车轮半径;ω为车轮滚动角速度;v为车轮前进线速度.
在该定义中,滑转率s的范围为[-1,l].当车轮滚动速度大于实际前进速度,车轮处于滑转状态,此时s>0;当车轮滚动速度等于实际前进速度,车轮处于纯滚动状态,此时s=0;当车轮滚动速度小于实际前进速度,车轮处于滑移状态,此时s<0;在普遍情况下,平地运动或爬坡时,车轮滑转率s≥0;车轮下坡时,滑转率s<0.
2.2轮壤相互作用力学模型
当车轮处于被动滑转状态时,轮壤相互作用力学模型如图3所示,星球车车轮在星球表面运动类似于车轮与松软地面相互作用的情形.图3中:ω为星球车车轮转动角速度;T为车轮转动力矩;?DP为挂钩牵引阻力;形为车轮正压力;υ为车轮实际前进线速度;r为车轮半径;从车轮竖直位置到接人土壤位置所对应的轮心角为接近角角θ1;从车轮竖直位置到离开土壤位置所对应轮心角为离去角θ2∶σ(θ)为车轮径向应力分布函数;τ(θ)为车轮剪切应力分布函数;θM为车轮最大径向应力所对应的轮心角,松软土壤对驱动车轮的作用力可以表现为连续的应力形式,即径向应力σ(θ)和剪切应力τ(θ),应力在车轮上的连续作用平衡于挂钩牵引阻力和车轮压力,
基于Wong-Reece的研究成果[16],可以得到车轮径向应力分布函数:式中:κc为土壤粘聚模量,κ为土壤摩擦模量,n为变形指数,6为车轮宽度,C1和c2为土壤最大应力角系数,c3为土壤离去角系数,结合Janosi的塑性剪切特性模型[17]和式(l)可以得到车轮剪切应力分布函数:式中∶c为土壤内聚力;γ为土壤内摩擦角;j(θ)为驱动车轮剪切位移;jo为剪切应力一位移曲线模量.
当车轮处于稳定状态时,挂钩牵引力F〈sub〉DP〈/sub〉、法向支持力Fn与车轮受到的挂钩牵引力阻力fDP、车轮正压力W相互平衡,对车轮径向应力和剪切应力进行积分,可以得到式(7).
3 滑转率估计方法研究
3.1 轮壤作用模型参数关系分析
基于以上对轮壤相互作用模型的分析,式(7)是非线性与高度耦合的积分方程组,挂钩牵引力和法向支持力是关于滑转率、轮壤作用接触角、车轮参数及土壤参数的函数,轮壤相互作用模型参数关系如图4所示,径向应力分布函数σ(θ)描述了在轮壤接触范围内驱动轮受到沿半径方向的应力分布,体现了土壤的承压特性[18],由土壤粘聚模量κ、摩擦模量k。、变形指数n、车轮半径r、车轮宽度6和接触角θ1、θ2、θm所决定,θ2是关于最大离去角系数c3,与θ1的函数,θM是关于最大应力角系数c1、c2、θ1与滑转率s的函数.剪切应力分布函数τ(θ)描述了土壤对驱动轮沿切向的应力分布,体现了土壤的剪切特性[19],由内聚力c、土壤内摩擦角γ、径向应力函数σ(θ)、车轮剪切位移j(θ)和剪切应力一位移曲线模量j0决定,j(θ)是关于车轮半径r、接触角θ1,以及滑转率s的函数.
车轮的正压力W决定了土壤对车轮的径向应力,同时剪切应力的在垂直方向上的分量对车轮有一定支撑作用.挂钩牵引力阻力fDP决定了车轮受到的剪切应力,并且径向应力的水平分量对车轮也有一定牵引作用.
3.2估计方法研究
通过轮壤相互作用模型参数关系解析,在车轮参数、土壤参数已知以及车轮正压力、挂钩牵引力阻力恒定的情况下,车轮被动滑转时基于式(7)”r以求解滑转率s和接触角θ1、θ2,具体求解流程如图5所示.当不考虑土壤回弹部分对车轮的影响时,离去角θ2,忽略为0,即离去角系数c3为0;当考虑土壤回弹部分对车轮的影响时,通常采用经验公式θ2=-0.125θ1,,离去角系数c3为-0.125,本文中对滑转率进行估计采用后者.因此,在车轮稳定运行状态下,利用式(7)可以求解滑转率s和接近角θ1.由于该方程组无解析解,需要经过多次迭代来求得方程组解,因此利用Matlab编写程序,采用fsolve函数进行求解.
针对驱动轮性能参数进行求解方式,基于被动滑转原理和基于主动滑转原理在已知参数和求解参数上有较大不同,基于被动滑转原理求解是将挂钩牵引力阻力fDP和车轮正压力W作为已知参数,利用方程组求解滑转率s和接近角θ1;基于主动滑转原理求解是将滑转率s和车轮正压力W作为已知条件,结合方程对车轮发生沉陷时的接近角θ1进行求解.相较于基于主动滑转原理对车轮性能参数进行求解的方式,基于被动滑转原理的求解更加复杂,但星球车在运行过程中滑转率往往处于未知状态,因此该方法更加贴近实际运行状态,求解出的滑转率在星球车控制应用中具有重要意义.
4 试验验证及结果分析
试验采用松软干沙模拟星球土壤,通过设置稳定的挂钩牵引力和车轮轮压进行车轮被动滑转试验.干沙力学参数如表l所示.
通过车轮一土壤相互作用试验,测得车轮稳定运行时的数据作为试验结果,针对同样的挂钩牵引力和车轮轮压的试验重复3次,并求取平均值作为最终试验数据,以确保试验数据的准确性,
被测轮半径400mm,宽度125mm,通过对车轮一土壤相互作用试验数据统计,可以得到在挂钩牵引阻力分别为40N、60N和80N下滑转率随车轮压力变化的曲线,如图6所示.
从试验结果可以看出,当挂钩牵引阻力一定时,无论是通过模型计算的滑转率还是经过试验得到的滑转率都随着车轮压力增大而减小,并且减小的速度逐渐变缓;在一定车轮压力下,车轮挂钩牵引阻力越小,引起的滑转率越小,
图6(a)中试验滑转率与理论滑转率两者之间卡H对误差为0.6%-8%;图6(b)中两者之间相对误差为1%-9.2%;图6(c)中两者之间相对误差为1.3%-9.6%.以上结果表明滑转率的相对误差能够维持在10%以下,验证了积分模型和滑转率估计方法的合理性与正确性.
4 结 论
在地面力学和被动滑转原理研究的基础上,建立了星球车车轮一土壤相互作用力学积分模型,推导了基于滑转率的车轮挂钩牵引力和支持力的解析表达式.基于对模型参数之间耦合关系的分析,系统研究了车轮滑转率的估计方法.结合轮壤相互作用试验及试验数据,通过比较模型计算的滑转率和车轮实际的滑转率,验证了积分模型和滑转率估计方法的合理性与正确性.

