基于带宽最大化的城市干线子区划分技术研究
唐小军,赵胜川,章立辉
(1.大连理工大学交通运输学院,辽宁,大连116024;2.浙江大学交通工程研究所,杭州310058)
基于带宽最大化的城市干线子区划分技术研究
唐小军1,赵胜川1,章立辉*2
(1.大连理工大学交通运输学院,辽宁,大连116024;2.浙江大学交通工程研究所,杭州310058)
针对以直行车流为主要流向,实行两相位控制的城市干线,基于经典的MAXBAND模型,建立了干线分子区协调控制模型.该模型自动将干线分为若干具有3–6个交叉口的控制子区,每个子区追求最大化绿波带宽,不同子区协调方向的直行车辆享有尽可能均等的绿波通行时间.采用遗传算法求解模型,求解结果显示,分段点一般为周期相对较大或间距较大的交叉口.通过与Synchro优化方案相比,本文模型优化的方案可以使子区的平均带宽有效率提高27.8%.利用CORSIM对分别采用本文模型和Synchro划分的6种配时方案进行仿真,结果表明,与后者优化的方案相比,本文模型优化的方案具有更优的干线平均延误、平均车速、停车率等性能指标.
交通工程;子区划分;超长干线;协调控制;遗传算法
1 引言
干线协调控制是避免或缓解干线交通拥堵有效且广泛使用的方法之一.一般来说,采用两类标准进行协调配时设计:最大化绿波带宽和最小化性能指标,如延误、排队长度等.Yang[1]将两种方法分别运用于一条具有9个信号控制交叉口的干线,发现前者的控制效果一般优于后者的控制效果.同时,由于前者能够满足驾驶员希望以更少的停车次数通过干线的期望,因此也被大多数的交通工程师和驾驶员所喜好.本文采用前一种方法建立相应的干线分子区协调控制模型.
绿波带宽具有这样一种本质[2]:随着干线交叉口数量的增加,带宽宽度会逐渐减小.马楠等[3]通过研究发现,当信号灯数量增加至16个时,很难获得全局带宽.表明将具有超过16个交叉口的干线作为整体实施协调控制并不是明智的做法.克服这一问题行之有效的方法之一是实行分子区协调控制.
进行子区划分的常用指标有3种,即关联度、吸引强度、协调因子[4].上述3种指标主要是考虑相邻交叉口的车流量、路段距离、路段车速、周期长度等因素,来决定是否对相邻交叉口实行协调控制.然而,不论上述指标计算过程简单或是复杂,其决定分段点的阈值是基于经验判断的,具有较强的主观性.当上述方法应用于多条连续路段具有相似指标值的干线时,会导致划分出较庞大的子区,这显然是缺乏一定合理性的.
此外,陈宁宁[5]提出了以协调控制目标为辅的路网控制子区划分方法,在符合距离、流量、周期三原则的基础上,要求信号控制子区必须有足够大的绿波宽度;Tian等[6]提出了一种启发式方法,根据交叉口之间的距离、车流量和排队情况及交叉口的饱和度将长干道划分为具有3–5个交叉口的子区,对每个子区实行绿波最大化控制,然后调节子区间相位差对整个系统实行单向绿波最大化控制;Zhang等[7]提出首先利用K均值法对干线进行子区划分,然后利用PASSER-Ⅱ对分区进行协调配时参数优化的干线分子区协调控制方法.由上述分析可知,对子区进行划分主要是依据相邻交叉口间距、路段交通量、排队长度及交叉口配时等参数,未见直接以绿波带宽度为优化目标的干线分子区协调控制研究.
本文基于经典的MAXBAND模型,以绿波带宽度为优化目标,建立干线分子区协调控制模型.该模型避免了传统方法分段点判断阈值具有主观性的缺点,同时可以保证每个子区最优的协调控制效果.
2 干线控制子区划分方法
2.1 MAXBAND模型简介
MAXBAND模型是由Little于1966年提出的[8].图1描述了相邻交叉口间绿波带的几何关系,图中水平横线表示红灯时间,空白线表示绿灯时间.令Sh、Si为任意一对相邻信号灯,且Si在Sh的出口方向.其中ri为路段上信号灯i的红灯时间;b、分别为信号灯i出口、进口方向通过带带宽;分别为从信号灯h(i)到i(h)沿出口、进口方向的行程时间;分别为从Sh、Si的红灯中心到Si、Sh的红灯中心的时间;wi、分别为从Si红灯时间的右侧、左侧到绿波带宽的时间;m(h,i)必须为整数.
MAXBAND模型的混合整数规划如下:
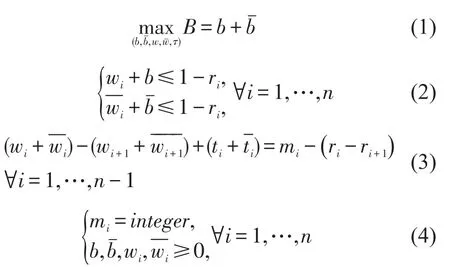

图1 绿波带的几何关系Fig.1 Geometry ofgreen bandwidth
2.2干线子区划分模型
上述模型适用于交叉口数量较少的干线.本文在经典MAXBAND模型的基础上,建立了适用于长干线的分子区协调控制模型.
2.2.1 目标函数
为了保证子区的协调控制效果,子区的优化目标为最大化双向绿波带宽,即

式中Bm为第m个子区的双向绿波带宽之和;bm为第m个子区出口方向绿波带宽;为第m个子区进口方向绿波带宽.
在实际道路上,交通流量在干线上的分布是不均匀的.对于流量较大的子区,我们希望提供其更大的总绿波带宽时间;流量相对较小的子区,提供其相对较小的总绿波带宽时间.为了保证各子区干线直行车辆享有更公平的绿波通行机会,定义Em,表示单位小时内第m个子区协调方向直行车辆的平均绿波通行时间,s/pcu/h;为各子区Em均值.显然,最理想的状况为即干线所有直行车辆在各子区享有相同的绿波带宽时间.因此,模型总目标为使各子区Em变化最小,则有

2.2.2 子区约束条件
将n个信号灯编号为1,2,…,n-1,n,路段编号为1,2,…,n-1.引入二进制变量其含义为

(1)子区信号周期约束.
对于具有不同分区的干线来说,由于各子区流量等因素的差异,各子区可能采用不同的周期.本文设置子区信号周期约束条件为:周期上/下限为子区内最大周期加/减10 s.zm为第m个子区的公共周期.

(2)子区信号灯数量约束条件.
显然,一个信号灯只能划分在一个子区中.同时,为了保证子区的协调控制效果,设置每个子区内信号灯数量为3–6个.

(3)子区信号灯连续性约束条件.
对于划分在同一子区内的信号灯而言,其编号必定是连续的.分析同一子区内信号灯和路段的关系.
(a)对于同一子区而言,信号灯数量比路段数量多1.

(b)如果一条路段在某子区内,则必有与其连接的两个信号灯也属于该子区;如果一条路段不在某子区内,则至少有一个与其连接的信号灯不属于该子区.即有

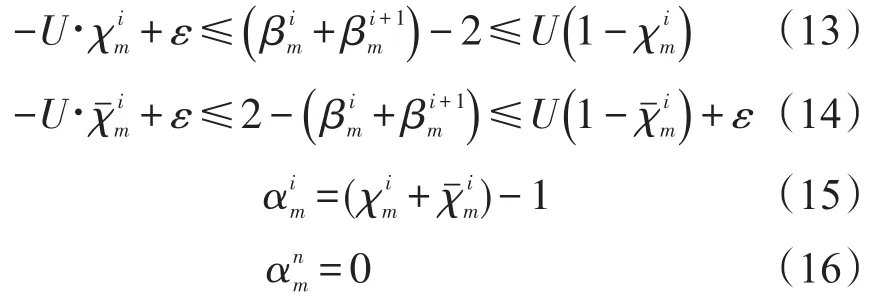
式中U为一足够大的正数,如9 999;ε为一任意小的正数,如0.001.
2.2.3 子区划分模型
为了进行模型的求解,我们将MAXBAND模型的约束条件乘以相应的二进制变量.则本文建立的基于带宽的分子区协调控制模型可表示为


2.2.4 子区间相位差计算
由于各子区信号周期可能不同,难以在分段点间获得稳定的行进带宽.为了简化研究,本文采用文献[9]提出的公式计算分段点间的相位差,然后再进行以交叉口1为起始参考点的相位差相对化处理.
3 Synchro信号配时软件简介
Synchro软件是著名的交通信号配时设计/通行能力分析及仿真商业软件[10].该软件以最小化性能指标为优化目标,能够同时优化信号交叉口周期、绿灯时长、相位相序、相位差等参数.其通过考虑路段行程时间、排队、流量等参数计算协调因子,以判断是否对相邻交叉口实行协调控制.但协调因子的计算是具有高度经验性的,因此从某种程度上来说,该方法缺乏一定合理性.但作为划分方案的比较评价,仍具有一定的参考意义.
4 模型求解
本文采用遗传算法求解模型.其好处在于可将模型转化为求解多个小型线性规划问题.另一方面,由于本文的研究范围为具有20个信号灯的主干线,因此求解规模是较小的,可以确保得到全局最优解.模型求解步骤如下.
Step 1染色体配置.
确定子区分段数后(4段、5段或6段),对初始解进行编码,每四位基因代表一个子区末端分段点.但需保证首四位基因的实值大于或等于3且小于或等于6,末四位基因的实值大于或等于15且小于或等于17.同时,前后串实值也需满足子区信号灯数量约束条件.如染色体000001101101表示划分方案为1-3,4-9,10-15,16-20.
Step 2适应度计算.
采用目标函数作为适应度计算公式.
Step 3产生父代.
首先用最好的个体替换最坏的个体,将其设为父代第一个个体,然后采用随机联赛机制产生其余父代.
Step 4交叉.
为了提高种群多样性,本文采用多点交叉.因为在进行交叉操作后,必须判断前后串实值关系.如果子区约束条件仍满足,则产生新个体;否则,重新进行交叉操作.交叉率取0.9.
Step 5变异.
同交叉操作一样,变异操作后同样需进行前后串实值关系判断.变异率取0.001.
Step 6循环迭代.
重复Step 2–Step 6,至最大迭代次数,取10.
5 数值算例分析
5.1 算例路网
利用模型对一条具有20个信号灯的双向六车道干线实行分子区协调控制,该干线不存在明显的地理分割特征.考虑到经典MAXBAND模型主要适用于干线直行车流为主且支路转入干线车流小的交通条件,本文将Synchro中的左转交通流设为允许左转,交叉口为定时两相位控制,各交叉口初始周期由Synchro优化所得.路网数据如表1所示.

表1 路网数据Table 1 Data ofnumericalexam p le
5.2 分段及配时方案比较
保持交叉口间距不变,利用表1的原始数据(后文称为demand 1)产生另外两组数据(demand 2和demand 3).其中demand 2是将demand 1的数据进行倒序排列,demand 3是将demand 1的后十组与前十组数据互换.利用本文模型对上述3种交通场景进行子区划分及配时方案计算.分区结果如表2所示.
由表2可知,对于每种流量组合而言,尽管分段数不同,但是分段点大致相同,且流量相对较大或距离相隔较远的交叉口在3种分段方案中一般都成为分段点.如demand 1中的5、8、14;demand 2中的7、16及demand 3中的8、9.
利用Synchro生成9种对比方案.为了保证方案的公平性,我们使Synchro 9种方案中的路段设计速度与模型优化的9种方案的设计速度对应保持一致.其分段结果如表3所示.

表2 模型分段结果Table 2 Partitioning results generated byModel

表3 Syn ch ro分段结果Table 3 Partitioning results generated by Synchro
由表3可知,Synchro划分在同一子区内的交叉口数量是没有限制的.由于其在划分时没有考虑最终的协调控制效率,可能会导致子区的绿波带宽很小,甚至无法得到子区带宽.而本文模型考虑了子区内信号灯数量对带宽的影响,可保证每个子区具有足够的带宽.由表2和表3计算可知,Synchro为各子区提供的平均带宽有效率为36%(不计单个交叉口),而本文模型能够提供高达46%的平均带宽有效率,提高率为27.8%.带宽有效率由式(17)计算.

式中Ba为出口方向带宽(s);Bb为进口方向带宽(s);C为公共周期(s).
平均带宽有效率即为每种划分方法下的9种分段方案所有子区带宽有效率的均值.值得注意的是,不同于由模型优化所得平均带宽有效率(46%),Synchro显示的带宽包含了黄灯时间(本文设为3 s),因此计算的平均带宽有效率(36%)实际上会偏大.
5.3 CORSIM微观仿真评价
各子区更大的绿波带宽,意味着干线直行车辆能够以更少的停车次数通过干线.但是基于带宽的协调配时方法存在一定的局限性,即在优化时没有考虑交通流和交叉口的通行能力,因此并不一定能优化其他与延误有关的性能指标[11].另外,由于协调车流在分段点处容易被信号灯打断,可能引起额外的延误.而Synchro则以最小化路网性能指标,包括控制延误、排队延误和停车数为优化目标.为了评价模型的控制效果,采用demand 1下的6种配时方案进行CORSIM仿真.每种方案采用不同的随机种子数仿真10次,仿真均值如表4所示.其中延误为干线双向平均车均延误,停车率为总的停车数除以总的通过车辆数.

表4 微观仿真结果Table 4 Results of simulation
由表4可看出,本文提出的方法在干线3项评价指标中均具有一定程度的优势.对于本算例而言,本文模型优化的3种分段方案具有相似的控制效果.就干线延误及停车率而言,分为5段的控制方案最优,其主要原因是该方案提供的干线绿波带宽时间最大.分为6段的方案具有最大的平均速度,因为其路段设计速度最大.由此分析可知,分段数增加时,协调控制效果不一定会变得更好.
6 研究结论
本文建立的干线分子区协调配时模型是可行的.本文针对传统干线子区划分方法存在分段点判断阈值具有主观性的缺点,基于经典的MAXBAND模型提出了干线分子区协调配时模型.该模型计算的分段点一般为周期相对较大或间距较大的交叉口.与Synchro优化的配时方案相比,本文模型使得平均带宽有效率提高了27.8%,且具有更优的控制效果.
本文模型并未考虑左转相位的优化问题,但对于考虑左转的模型也可以通过本文提出的类似方法进行建模和求解.
[1]Yang X K.Comparison among computer packages in providing timing plans for Iowa Arterial in Lawrence,Kansas[J].Journal of Transportation Engineering,2001,127(4):314–318.
[2]Lin L T,Tung L W,Ku H C.Synchronized signal control model for maximizing progression along an arterial[J].Journal of Transportation Engineering,2009,136(8):727-735.
[3]马楠,邵春福,赵熠.干道信号交叉口群协调控制系统中的影响因素[J].哈尔滨工业大学学报,2011,43(6):112-117.[MA N,SHAO C F,ZHAO Y. Influence factors of coordination control system in signalized intersections[J].Journal of Harbin Institute of Technology,2011,43(6):112-117.][4]Hook D,Albers A.Comparison of alternative methodologies to determine breakpoints in signal progression[C]//In Compendium of Technical Papers for the69th AnnualMeetingof the ITE,1999.
[5]陈宁宁.信号控制子区动态划分及区域自适应协调控制研究[D].广东:中山大学,2010.[CHEN N N. Research on sub-area dynamic division and adaptive coordinated signal control[D].Guang dong:Sun Yat-Sen University,2010.
[6]Tian Z,Urbanik T.System partition technique to improve signal coordination and traffic progression[J]. Journal of Transportation Engineering,2009,133(2):119-128.
[7]Zhang T,Zhang Y.System partition method to improve arterial signal coordination[C]//Transportation Research Board 93rd AnnualMeeting,2014.
[8]Little J D C.The synchronization of traffic signals by mixed-integer linear programming[J].Operations Research,1966,14(4):568-594.
[9]罗斯罗格,普拉萨丝艾琳娜,米山尼威廉姆.交通工程(应用)[M].北京:机械工业出版社,2008.[Roger P R,Elena S P,William R M.Traffic engineering (Application)[M].Beijing:ChinaMachine Press,2008.
[10]Husch D,Albeck J.Synchro 6:Traffic signal softwareuserguide[M].Trafficware Limited,2003.
[11]Zhang L,Yin Y.Robust synchronization of actuated signals on arterials[J].Transportation Research Record: Journal of The Transportation.Research Board,2008,2080(1):111-119.
System Partition of Urban A rterials Based on Bandw id th Maximization
TANG Xiao-jun1,ZHAO Sheng-chuan1,ZHANG Li-hui2
(1.Schoolof Transportation and Logistics,Dalian University of Technology,Dalian 116024,Liaoning,China;2.Institute of Transportation Engineering,Zhejiang University,Hangzhou 310058,China)
A system partitionmodel for urban arterials is proposed based on classical MAXBAND model. Themodel divides thewhole arterial into several subsystems,each with three to six signalized intersections. Each subsystem is optimized individually to achieve maximum two-way bandw idth.The through traffic in different subsystems is provided average green bandw idth as equalas possible.Genetic A lgorithm is applied to solve themodel,the optimal results implies that intersectionswith critical cycle length or large spacing is the partitioning point.Compared to the plan generated by Synchro,the one produced by the proposedmodel increases the average progression efficiency by 27.8%.CORSIM simulation is conducted to compare the performance of signal timing plans generated by the proposed model and Synchro respectively,and results analysis indicates that compared to the plan generated by latter one,the one produces by former one resulted in better performance indexes,such asaverage delay,average speed and stops.
traffic engineering;system partition;super-long arterial;coordination control;genetic algorithm
1009-6744(2015)03-0100-07
U491.54
A
2014-12-08
2015-03-29录用日期:2015-04-14
国家自然科学基金项目(51278087,71401025).
唐小军(1989-),男,四川德阳人,硕士生.*通信作者:lihuizhang@zju.edu.cn

