正交试验设计在散热器结构优化中的应用
金阳 赵树兴 任销锋 马江辉
天津城建大学能源与安全工程学院
正交试验设计在散热器结构优化中的应用
金阳 赵树兴 任销锋 马江辉
天津城建大学能源与安全工程学院
本文将纯铝散热器散热量设为目标函数,以正交试验设计思想为理论基础,利用Matlab软件模拟某一结构散热器,用试算法对不同结构尺寸纯铝散热器散热量进行计算,求出影响纯铝散热器散热量的主要结构因素,为以后实验提供简单、快捷的方法,具有实际意义。
散热器 Matlab 正交试验 试算法
随着国内经济快速发展,建筑总面积逐日上升,散热器需求也逐日增高,散热器散热量是衡量散热器的重要指标,由于散热器型号及种类繁多,若都采用实验方法来测定其散热量必将带来繁琐的工作。数值计算是一种有效、简便、快捷计算散热量的方法,通过建立合理的数学模型,运用计算机语言对数学模型进行编程,能有效提高散热器散热量的计算速度[1],本文重点研究改变纯铝散热器的结构尺寸,运用正交试验方法思想,算出不同结构尺寸散热器的散热量,分析影响纯铝散热器散热量的主要结构因素,为以后实验提供简单、快捷的方法。
1 正交试验设计与建模
1.1 正交试验设计及数据处理方法
正交试验设计[2],是利用规格化的正交表,恰当地设计出试验方案和有效地分析试验结果,提出最佳配方和工艺条件,并进而设计出可能更优秀的试验方案的一种科学方法。
极差法又叫直观分析法。极差是指某因素在不同水平下的指标值的最大值Kn与最小值Km(n、m=1、2、3、4……)之间的差值R,极差的大小反映了试验中各个因素影响的大小,极差大表明该因素对试验结果的影响大,是主要因素;反之,极差小表明该因素对试验结果的影响小,是次要因素或不重要因素。根据极差的大小,分析各个因素对试验指标值的影响程度,确定主次因素,从而找到主要因素的最好水平。
1.2 试验方案设计
正交试验最重要的就是“挑因素”“选水平”,鉴于对研究时间及试验次数的考虑,选定了4个考察因素。表1所列的是本文研究选定的因素和水平。根据因素和水平数,选择了L9(34)正交表,由该正交表可以确定出9种试验方案。

表1 正交试验考察因素及其水平
1.3 散热器几何模型
本文以单柱双通道纯铝散热器为研究对象,其模型平面图如图1。该散热器模型高510mm,长为100mm,热水通道壁厚1.8mm,肋片宽1.2mm。热水进口温度95℃,出口温度70℃,室内设计温度18℃[3]。

图1 模型平面图
1.4 散热器数学模型
1.4.1 热水通道数学模型对于散热器,有[4~5]:

经过计算Re<2300,流体为层流,所以[6]

式中:Q为假设热水通道换热量,W;cs为热水的比热容,J/(kg℃);ρs为热水密度,kg/m3;vs为热水流速,m/s;Ah为热水通道横截面积,m2;fs为热水通道内水平均温度为82.5℃时粘度系数;Re为热水状态参数,当小于2300为层流;Pr为热水平均温度为82.5℃无因次数;l为热水通道的高,m。λs为热水平均温度为82.5℃的导热系数;twn为热水通道内壁温度,℃;tww为热水通道外壁温度,℃;δs为热水通道壁的厚度,m;λ为铝的导热系数,W/(m·K)。As为热水与热水通道热交换面积,m2。
1.4.2 空气对流数学模型
对于散热器空气对流换热,有:


式中:m1为肋片换热系数,1/m;h1为假设空气对流换热系数,W/(m·K);δ为肋片厚度,m;tw1为肋端温度,℃;l为肋片长度,m;g为重力加速度,m2/s;a1为温度系数,1/K;H为肋片高度,m;v1为空气运动粘度系数;Pr1为普朗特数;Q1为空气对流换热量,W;h11为计算出空气对流换热系数,W/(m·K);A1为空气对流换热面积,m2。
1.4.3 表面辐射数学模型
对于散热器表面辐射,有:

式中:Q2为辐射换热量,W;σ为黑体辐射常数,5.67× 10-8W/(m2K4);ε为散热器表面发射率;T为壁面温度,K;Tf为环境当量温度,K。
1.4.4 散热器总热量
散热器总热量为:

式中:Q'为求解散热器换热量,W。
1.5 编程设计框图
本文使用试算法,首先假设目标散热量Q,假设自然对流换热系数h1,然后逐个验证,直到假设和验证相同,进而得出计算结果,如图2。
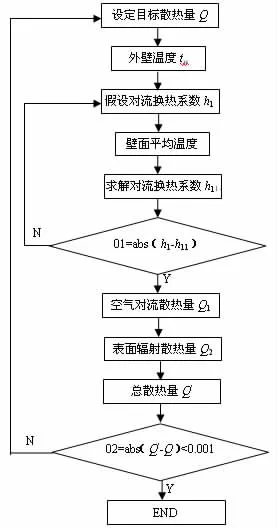
图2 设计框图
2 计算结果及分析
本文用Matlab计算,得到9种不同的方案的散热量,如表2。

表2 试算方案一览表
根据表2,算出极差值R,如表3。

表3 影响因素分析表
从表3中可以看出对散热器散热量影响因素主次顺序分别是:发射率、肋片数、肋长、热水通道宽度。最优组合为A1B3C3D3。
3 结论
本文运用正交试验设计思想与Matlab软件模拟得出影响纯铝散热器散热量的主要结构因素。经过计算得到最优方案,即散热器肋长为20mm,肋片为9,发射率为0.9,热水通道宽度为14mm,其散热量为180W。对纯铝散热器结构进行优化,其发射率对其散热量影响较大,热水通道宽度影响相对较小。考虑到是单柱散热器,在实际应用过程还要进行组合,通常为3~4柱,所以在计算过程忽略散热器两侧的散热量,且并未考虑上下母管计算,其数值比实际值偏小。
本文运用正交试验设计方法思想,通过优化纯铝散热器的结构尺寸,算出其不同结构尺寸散热器的散热量,分析影响在某一结构形式下的纯铝散热器量的主要结构因素,为以后实验提供简单、快捷的方法,从而在以后实验过程更省事、省时、省料。
[1]刘硕,郭铁明.运用matlab计算散热器的散热量[J].暖通空调, 2010,40(8):131-134
[2]邱轶兵.试验设计与数据处理[M].合肥:中国科学技术大学出版社,2008
[3]中华人民共和国国家技术监督局.采暖散热器铝制柱翼型散热器(GB/T 143-2002)[S].北京:中华人民共和国建设部,2002
[4]翁运飞.铜管铝翅片对流散热器结构型式优化的研究[D].哈尔滨:哈尔滨工业大学,2008
[5]陈建芳,张双喜.散热器肋片的数值计算和结构优化[J].建筑热能通风空调,2004,23(2):77-80
[6]章熙民,任泽霈,梅飞鸣.传热学[M].北京:中国建筑工业出版社,1993
Orthogona l De s ign in Pure Ra dia tor Struc ture Optim iza tion
JIN Yang,ZHAO Shu-xing,REN Xiao-feng,MA Jiang-hui
School of Energy and Safety Engineering,Tianjin Chengjian University
This article will set the amount of aluminum radiator heat objective function,orthogonal design ideas based on the theory of a structure using Matlab software simulation radiator test algorithm with different structural dimensions to calculate the amount of aluminum radiator cooling,seeking aluminum radiator heat that affect the amount of the main structural factors for future experiments to provide a simple,quick method has practical significance.
radiator,Matlab,orthogonal test,test algorithm
1003-0344(2015)01-072-3
2013-10-30
金阳(1988~),男,硕士研究生;天津市西青区津静公路26号天津城建大学能源与安全工程学院(300384);E-mail:jinyangyouxiang@163.com

