一种新型风口边界条件设置方法的研究

董素君王嫚鸽

北京航空航天大学航空科学与工程学院

一种新型风口边界条件设置方法的研究

董素君王嫚鸽

北京航空航天大学航空科学与工程学院

采用CFD方法对圆形喷口单股等温自由射流进行数值模拟研究，提出了一种新的用于风口模拟的盒子分区计算模型。先将计算结果与Elsaadawy（1998）、Hussein（1994）实验数据和经典射流公式进行对比，选定合适的湍流模型，后通过对盒子分区计算模型的结果分析对比，说明该模型的可行性，为复杂风口大空间流场计算提供了一种新的思路。

圆形射流 CFD模拟 风口模型

0 引言

在对室内气流组织的探索研究中，风口模型的简化问题一直是众多学者研究的对象。尽管人们已经对气体流动的CFD模拟进行了大量的研究[1～3]，但是在实际应用中，结构复杂的送风口的模型构建仍然是一个难题[4]。

复杂的送风口结构使得对气流开始端的边界条件的描述变得尤其困难，对于边界条件不精确的简化进而会导致在随后的气流模拟和预测中出现偏差[5]。20世纪90年代以来，工程中常用的风口结构模型有动量模型、盒子模型、N点动量模型和主流区法[6]。动量方法是用一个与原风口或散流器外形尺寸一样的矩形开口来代替，假定风口上动量分布均匀，并将入口动量置为实际空气的入口动量。动量方法不易操作，难以在通用软件上实现。盒子方法是将边界条件设置在距离风口有一定距离的盒子表面，平行于风口入流面上的各个参数通过测试或由风口射流特性公式得到，而其他面上的参数当作平行流[7]。但是盒子方法无法应用于以一定角度射流的情况。N点动量模型是用N个简单的开口替代实际送风口，对任一个简单开口，入流动量流量按照动量方法来计算[8]。该模型的优势在于能够处理多喷嘴送风口问题，对送风方向和送风口的规则性没有限制，但是对于边界条件的确定仍然需要借助样本或测量数据。1996年，Yan Huo等人提出了“主流区法”(Main region specification method)来描述风口边界条件[9]。王志刚[10]等人在2008年针对四种风口模型的简化方法对办公室内的空气流动进行数值模拟，分析认为“主流区法”优于基本模型、盒子模型和N点模型。

在以上所述的众多风口简化方法中，盒子模型思想较为突出，如指定速度法和主流区法都是在盒子方法的基础上，对边界条件的设置进行改进，使计算得到了优化。其中盒子模型和指定速度法的入口速度是利用实验测量得到的，不仅准确性不高，而且成本和难度都较大。主流区法速度入口值则是根据工程公式计算得到的，对经验公式依赖性高且有一定的局限性。

本文根据盒子模型的基本思想，针对实际工程计算中遇到的大空间多设备的复杂流场计算问题，对盒子模型边界条件的设置进行改进，用数值计算的结果作为入口的边界条件，以提高流场计算的准确性。

1 射流理论与射流公式

射流是指从各种排泄口射出或靠机械推动流入周围另一流体域的一股运动流体，它是工程实际中广泛存在的一种流动现象[11]。射流在形成稳定的流动形态后，一般可以分为起始段、过渡段和主体段，研究表明：主体段所有断面的无量纲流速或浓度分布曲线是相同的，这种现象被叫做自模性。对射流的研究主要集中于射流主体段。

射流按其断面形状可以分为平面射流（二维射流）、圆形射流（轴对称射流）、矩形射流等。下面本文将针对圆形射流进行具体的计算分析。

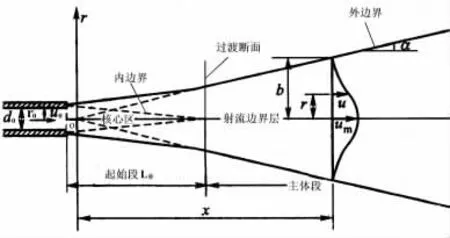
图1 自由射流示意图

根据射流理论[13]，射流分为起始端和主体段，在环境控制中主要是应用主体段，主体段的轴心速度分布情况如下式：

式中：vx为距离喷口x处的射流轴心速度，m/s；v0为喷口的射流速度，m/s；x为射流截面至喷口的距离，m；d0为喷口直径，m；β为喷嘴紊流系数。

其中，射流的紊流系数β反应射流截面上速度不均匀程度的影响，其值取决于射流喷嘴的结构类型。另外，β值的大小直接影响到射流扩散情况，β值小，即气流横向脉动小，扩散角也就小；当β值一定时，射流按一定的扩散角扩展，即射流几何形状也就一定。查表得到圆形截面射流紊流系数的值β=0.076[12]。

Elsaadawy[13]和Hussein[14]分别于1998和1994年对圆截面射流进行了相关实验。其中Elsaadawy的实验中分别取雷诺数为7200和13000，为了便于研究对比，本文取Re=7200的圆截面射流进行数值计算。图2是在雷诺数为7200时，工程经验公式和Elsaadawy实验数据的比对曲线。

图2 射流公式与实验结果进行对比

由于射流经验公式的适用范围是主体段，其数据是从主体段开始的。从上图可以看出，射流公式的计算与实验测得的数据基本上是吻合的，从而也证明了经验公式对圆形射流的适用性。

2 CFD模拟

本文针对简单圆截面射流进行仿真计算，基本模型是指直接对圆截面射流的计算，盒子模型是指将射流入口罩在选定的盒子中，在盒子各个面上赋予相应的边界条件，通过计算对比，证明盒子分区计算模型的可行性。

2.1 基本模型的数值计算

基本模型的计算是为了与盒子分区计算模型的计算结果作对比分析，以验证盒子分区模型计算的准确性。为了保证计算结果的可比性，基本模型和盒子模型的网格划分是一致的。

2.1.1 基本模型的建立

本文考虑到射流出口为圆断面，出流空间为高大空间，建立如下圆管形空间网格如图3，射流入口直径D为8mm，计算模型的计算区域设定为底面直径20D，长度L为50D。本文仅考虑单股等温湍流自由射流情况，流动为标准密度和粘度下的不可压缩湍流流动，选取连续相为25℃的空气的圆射流进行数值模拟计算。利用ICEM网格划分软件对计算模型进行网格划分，保证圆湍射流计算模型网格全部为六面体网格以减少网格质量差造成的伪扩散。

图3 圆射流几何模型和计算网格示意图

图4 圆射流沿X和Y方向的网格分布

2.1.2 边界条件的设置

本文选取了k-ε二方程模型以封闭N-S方程组，使用SIMPLE算法[11]对离散方程进行迭代求解计算。

1）进口：采用速度入口，入口给定湍流强度取值为，水力直径D。

2）出口：采用压力出口，考虑到圆射流数值模拟计算所需空间较大，需保证大空间射流，故而选择Pressure outlet。

2.1.3 数值计算与结果分析

通过对气相圆射流数值仿真结果，并根据上节射流理论将其与经验公式计算结果进行分析对比，以期对圆射流进行深入的了解。数值仿真分别采用Realizable k-ε、RNG k-ε和RSM三种不同的湍流模型，并与Elsaadawy（1998）[13]、Hussein（1994）[14]实验数据比较，探讨计算圆湍射流的最佳模型。

图5 不同湍流模型与实验测量数据中心轴线上平均速度分布

Realizable k-ε、RNG k-ε和RSM模型的数据分析与实验对比后，可知由Elsaadawy（1998）的实验数据可知Re=7200圆射流的射流核心区长度应为4.7D，而这个实验值也符合Ko&Davies[15]的研究结果相符合。从图5不同湍流模型与实验数据中心轴线平均速度分布图可以看出，RSM、realizable k-ε和RNG k-ε在射流初始段的模拟结果与Elsaadawy（1998）的射流核心区实验值长度都较为符合，射流核心区长度基本上都在5D左右。但是在后面的计算中Realizable k-ε模型的数据更接近实验结果，故选择Realizable k-ε作为圆射流的数值计算模型。下面将对Realizable k-ε模型的各切面速度进行进一步的研究分析，以证明该模型的适用性。

图6～9描述了Realizable k-ε模型计算与实验数据平均轴向速度在自相似区（X/D=0.25、X/D=3、X/D= 10、X/D=20）的径向分布，其中r为径向上距离轴心的坐标值，X是轴向上距离射流入口的坐标值。可以看出Realizable k-ε模型在轴向速度沿径向分布的计算结果与Elsaadawy（1998）的实验结果相符。只有X=3D处Elsaadawy（1998）的实验结果射流宽度略大于LES的模拟结果。从而也证明了Realizable k-ε模型对圆射流的适用性。

图6 Realizable k-ε模型与实验测量平均速度沿（X/D=0.25）径向分布

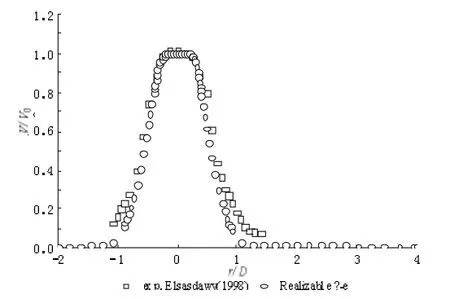
图7 Realizable k-ε计算与实验测量平均速度沿（X/D=3）径向分布

图8 Realizable k-ε计算与实验测量平均速度沿（X/D=10）径向分布

图9 Realizable k-ε计算与实验测量平均速度沿（X/D=20）径向分布

2.2 盒子分区计算模型的数值计算

本文为了解决更真实的模拟复杂出风口断面的速度分布问题，以大空间圆形射流为例，根据盒子模型的分区思想，假设出流空间为高大空间，先对风口进行数值计算，在合适的位置取截面计算结果作为下一步整个流场计算的入口条件。即对风口模型进行盒子划分后，前边风口数值计算结果作为盒子入口边界条件，复杂风口完全被盒子包括在里面，这样既能够给出较为准确可靠的入口边界数据，又避免了大空间流场的数值计算时对风口模型的细节描述，使风口模型的简化更加可靠准确、容易实现。

2.2.1 盒子分区计算模型的建立

结合当前风口描述方法的发展，和CFD计算条件的进步，提出了一种盒子分区计算方法，以解决复杂风口的简化问题。

根据射流轴心衰减公式（1），计算出该圆射流模型的初始段长为35mm，即在射流在轴心距离35mm处进入射流主体段。本文选择射流起始端与主体段交界处作为盒子入口面，盒子形状同外流场为圆柱形。对于圆截面自由射流，实验得出紊流系数β和扩散角α间的关系为式（2）。根据公式（2）确定盒子面半径为9.1mm。具体模型和网格如图所示：

式中：α为射流扩散角；紊流系数β取值如上文所述。

根据圆射流特性公式（1），计算出该圆射流模型的初始段长为35mm，此处取盒子面为R=9.1mm的圆柱体，几何和网格模型如下：

图10 盒子模型与轴向切面网格示意图

2.2.2 边界条件的设置

盒子分区计算模型入口边界条件的给定，需要在给定的盒子入口面加载Prof数据文件实现，即利用入口单独计算时得到的数据，导入盒子模型中相应的面作为入口边界条件：

1）盒子面入口：采用速度入口，加载数据文件，对应的湍动能k和湍流耗散率ε同样采用数据文件加载方式。

2）出口：和基本模型一致，采用压力出口边界条件。

2.2.3 盒子模型的数值计算与结果分析

经计算收敛，将盒子分区计算模型和基本模型的相关数据进行对比分析，得到以下结果具体分析如图11～12所示。

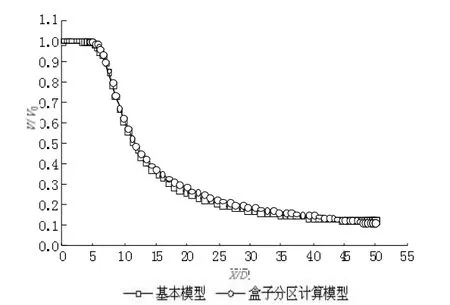
图11 盒子分区计算模型与基本模型中心轴线速度分布

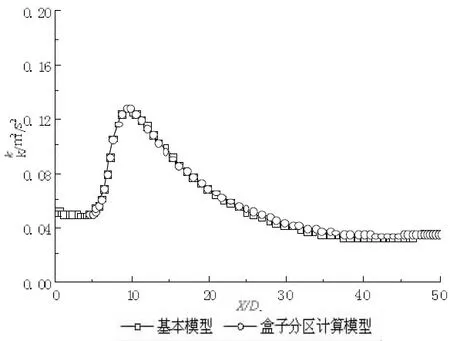
图12 盒子分区模型与基本模型中心轴线湍动能分布

从上图可以看到，基本模型和盒子分区计算模型，无论是轴心平均速度，还是轴心湍动能值都非常接近，证明了该方法的可行性。下面将进一步对两个模型的计算结果进行分析对比，以对两种方法的描述做更一个深入的了解。

图13～16描述了Realizable k-ε基本模型计算与盒子分区计算模型在自相似区（X/D=6、X/D=8、X/D= 10、X/D=20）的径向分布。可以看到，两个模型的平均轴向速度沿径向分布在X/D=6、X/D=8和X/D=10吻合度较高，而X/D=20时稍有偏离，说明速度场在模型的后段出现了一些不同，但其最高偏差为8%左右，对于工程计算来说是可以接受的。

图13 基本模型和盒子分区计算模型平均速度沿（X/D=6）径向分布

图14 基本模型和盒子分区计算模型平均速度沿（X/D=8）径向分布

图15 基本模型和盒子分区计算模型平均速度沿（X/D=10）径向分布

图16 基本模型和盒子分区计算模型平均速度沿（X/D=20）径向分布

为了能够更直观地比较两个模型的计算结果，从对称面各截取模型的一半，将其放在一起进行比较（图17～18）。可以看到，两个模型的速度流线和湍动能流线在射流的初期阶段吻合比较好，随着射流的深入，速度和湍动能都出现了一些差别，两者湍动能偏差最高达7%左右，这是由于射流边界条件的不同造成。从总体上看，整个流场的流线较为接近，再一次证明了盒子分区计算模型的可行性。

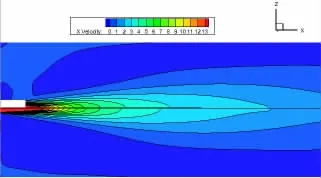
图17 基本模型和盒子分区计算模型的速度分布比对图

图18 基本模型和盒子分区计算模型的湍动能分布比对图

3 结论

本文首先分别应用Realizable k-ε模型、雷诺应力RSM模型以及RNG k-ε模型对Re为7200的圆射流流场进行数值计算，并与Elsaadawy（1998）的实验数据进行比较。通过对比分析，发现Realizable k-ε模型在计算圆射流总体上与实验数据最为吻合，且对于圆射流的实际流场计算最好。然后借鉴盒子的思想，建立了盒子分区计算模型，通过对盒子分区计算模型和基本模型的计算对比分析，发现其各方面数据吻合度都较高，证明了该模型的准确性和可行性，为大空间流场中复杂风口的简化计算问题提供了一个新的思路。

[1]杭寅,刘东,黄艳,等.某高层建筑空调室外机的气流模拟及优化[J].建筑热能通风空调,2006,25(3):12-16

[2]Kong Qiongxiang,Yu Bingfeng,Pan Zhen.Numerical simulation on airflow in plenum of underfloor air supply and experiment on characteristics of plenum's outlet[J].Journal of Xi’an Jiaotong University,2005,39(5):531-535

[3]Srebric Jelena,Vukovic Vladirnir,He Guoqing,et al.CFD boundary conditions for contaminant dispersion,heat transfer and airflow simulations around human occupants in indoor environments [J].Building and Environment,2008,43(3):294-303

[4]Chen Qingyan.Computational fluid dynamics for HVAC:Successes and failures[J].ASHRAE Transactions,1997,103(1):178-187

[5]杜国付,端木琳,舒海文.工位空调送风气流数值模拟风口模型的比较[J].热科学与技术,2003,2(2):162-167

[6]Nielsen P V.Description of supply opening in numerical models for room air distribution[J].ASHRAE Transactions,1992,98(1):963-971

[7]Nielsen P V,Restivo A,Whitelaw J H.Velocity tics of characteris ventilated rooms[J].Transactions ASME,Journal of Fluids Engineering,1978,100(3):291-298

[8]Chen Q Y,Moser A.Simulation of a multiple nozzle diffuser[A]. In:Proceedings of the 12th AIVC Conference[C].Ottawa,1991: 24-27

[9]Yan Huo,Jianshun Zhang,Chiayu Shaw,et al.A new method to describe the diffuser boundary conditions in CFD simulation[J]. ROOMVENT,1996:1-8

[10]王志刚,张于峰,苗哲生,等.主流区风口模型在CFD模拟中的应用[J].天津大学学报,2008,41(10):1252-1257

[11]赵清华,全学军.轴对称射流研究进展[J].重庆工学院学报, 2003,17(4):38-41

[12]寿荣中,何慧珊.飞行器环境控制[M].北京:北京航空航天大学出版社,2004

[13]H Warda,S Z Kassab,K Elshorbagy,E A Elsaadawy.An experim -ental investigation of the near-field region of free turbulent round central and annular jets[J].Flow Measurement and Instrumenta -tion,1999,10:1-14

[14]Hussein J,Steven P,CAPP.Velocity measurements in a high-Rey -nolds-number,momentum-conserving axisym metric turbulent jet[J].J.Fluid Mech,1994,258:31-75

[15]N W M KO,P O A L Davies.The near field within the potential cone of subsonic cold jets[J].J.Fluid Mech,1971,50:49-78

A Ne w Me thod for Bounda ry Condition Se tting of Air Supply Ope ning Mode l

DONG Su-jun,WANG Man-ge
School of Aeronautic Science and Technology,Beihang University

Using CFD method to study the isothermal round jet,a new partitioned box method for simplified air supply opening model was proposed.Firstly,Compare the results with Elsaadawy(1998)&Hussein(1994)experimental data, and then compare with the classic jet formula,select the appropriate turbulence model.Secondly,through contrast the result of partitioned box method with basic model,certifying the reliable and feasible of this model,provided a new way to forecast the complex air flow in a large space field.

round jet,CFD simulation,air supply opening model

1003-0344（2015）01-032-6

2013-10-13

董素君（1972～），女，博士，教授；北京市海淀区学院路37号北京航空航天大学新主楼c503（100191）；E-mail:winterstill@163.com