变精度粗糙集模型研究
黄卫华,杨国增,陆亚哲,周 平
(1.文山学院数学学院,云南 文山 663000;2.郑州师范学院数学与统计学院,河南 郑州 450044)
变精度粗糙集模型研究
黄卫华1,杨国增2,陆亚哲1,周 平1
(1.文山学院数学学院,云南 文山 663000;2.郑州师范学院数学与统计学院,河南 郑州 450044)
在经典粗糙集模型的基础上引入了参数β(0≤β<0.5),得到变精度粗糙集模型。讨论变精度粗糙集模型上、下近似算子的一些性质,即随着分类误差β的增大,X的正域与负域均扩大,边界缩小。同时通过经典的例子,说明变精度粗糙集模型相对于经典粗糙集模型其精确性提高了。
粗糙集;变精度粗糙集;近似算子
0 引 言
粗糙集[1]理论的核心问题是分类分析。经典粗糙集模型的一个不足是处理的分类必须是完全正确的或是肯定的,因为它是严格按照等价关系来分类的,因而分类是精确的;且所处理的对象是已知的,故从模型中得到的结论仅适合于这些对象集。但在实际应用中,往往需要将从小规模的对象集中得到的结论应用到较大规模的对象集中。Pawlak粗糙集模型的这些缺点限制了它的广泛应用。为了弥补该不足,许多学者从不同角度推广了经典粗糙集模型,如程度粗糙集模型[2-5]、变精度粗糙集模型等[6-11]、概率粗糙集模型[12]、模糊粗糙集模型[13-15]等。本文在经典粗糙集模型的基础上引入了参数β(0≤β<0.5),得到变精度粗糙集模型。
1 预备知识
定义1[11]设(U,R)为近似空间,其中U为非空有限论域,R为U上的等价关系,对于X⊆U,分别定义X的上、下近似,边界和负域为:
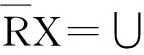
定义2[11]设X,Y表示有限论域U的两个非空子集,令

定义3[11]设X,Y表示有限论域U的2个非空子集,令0≤β<0.5,定义多数包含关系:

显然,Y⊇X当且仅当C(X,Y)=0。
下面举例说明多数包含关系。
例1 令X1={x1,x2,x3,x4},X2={x1,x2,x6},X3={x4,x6,x8},Y={x1,x2,x3,x7}。
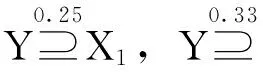

定义4[11]设(U,R)为近似空间,其中U为非空有限论域,R为U上的等价关系,U/R={E1,E2,…En}为R的等价类。对于X⊆U,分别定义X的β上、下近似,边界和负域为:
bnrβ(X)=∪{E∈U/R|β X的β下近似也成为β正域,记为posrβ(X)。 定理3 ∀X⊆U,下列关系成立:(1)posrβ(X)=negrβ(X),(2)若bnrβ(X)=∅,则posrβ(X)∪negrβ(X)=U。 (2)由(1)知,posrβ(X)=negrβ(X)并且bnrβ(X)=∅,则posrβ(X)∪negrβ(X)=posrβ(X)∪posrβ(X)=U。 设(U,R)为近似空间,其中U={x1,x2,…,x20,等价关系的等价类如下:E1={x4,x5},E2={x6,x7,x8},E3={x9,x10,x11,x12},E4={x1,x2,x3,x13,x14,E5={x15,x16,x17,x18},E6={x19,x20} 对于两度水平:β1=0和β2=0.25,计算X={x4,x5,x8,x14,x16,x17,x18,x19,x20}的近似。 如果β1=0,由定义4知,集合X的β近似集等于标准近似集。因此 bnr0X=bnRX=E2∪E4∪E5,negr0X=negRX=E3。 如果β2=0.25,则有 本文研究的变精度粗糙集模型是Pawlak粗糙集模型的推广,它是在经典粗糙集模型的基础上引入了参数β(0≤β<0.5),即允许一定程度的错误分类率存在。这一推广不仅丰富了近似空间中粗糙集的概念,也有利于粗糙集理论从不相关的数据中发现相关数据。变精度粗糙集的主要任务是解决属性间无严格意义上的函数关系或存在不确定关系的数据分类问题。当β=0时,变精度粗糙集模型退化为Pawlak粗糙集模型。最后同时通过一个实例,说明变精度粗糙集模型相对于经典粗糙集模型其精确性提高了。 [1]PawlakZ.Roughsets[J].InternJCompInformSci,1982,11(05):341-356. [2]张贤勇,谢寿才,莫智文.程度粗糙集[J].四川师范大学学报,2010,33(01):12-16. [3]ZiarkoW.Variableprecisionroughsetmodle[J].JCompSystemSci,1993,46:39-59. [4]吴志远,钟培华,胡建根.程度多粒度粗糙集[J].模糊系统与数学,2014,28(03):165-172. [5]顾力平,杨习贝.基于一般二元关系的多粒度粗糙集模型[J].南京航空航天大学学报,2013,45(01):124-129. [6]张贤勇,莫智文.变精度粗糙集[J].模式识别与人工智能,2004,17(02):151-155. [7]ZhangXY,MoZW,ShuL.Productapproximationofgradeandprecision[J].JElectrSciTechChina,2005,3(03):276-279. [8]申锦标,吕跃进.变精度与程度粗糙集的一种推广[J].计算机工程与应用,2008,44(36):45-47. [9]闫敏伦.新型变精度多粒化粗糙集模型[J].南京理工大学学报,2014,38(04):496-500. [10]许韦,吴陈,杨习贝.基于相似关系的变精度多粒度粗糙集模型[J].科学技术与工程,2013,13(09):2517-2522. [11]石梦婷,刘文奇,余高峰.变精度软粗糙集[J].计算机工程与应用,2014,50(01):101-104. [12]郭智莲,杨海龙,王珏.双论域上的直觉模糊概率粗糙集模型及其应用[J].系统工程理论与实践,2014,34(07):1828-1834. [13]翟俊海,张垚,王熙照.相容粗糙模糊集模型[J].山东大学学报,2014,49(08):73-79. [14]易涛,耿志强,徐圆,等.模糊粗糙集测度的分析分层建模及应急演练控制应用[J].控制理论与应用,2014,31(10):1368-1376. [15]赵明清.模糊粗糙集的三个数字特征[J].模糊系统与数学,2014,28(02):175-182. [责任编辑:郑秀亮 英文编辑:刘彦哲] Model of Variable Precision Rough Set HUANG Wei-hua1,YANG Guo-zeng2,LU Ya-zhe1,ZHOU Ping1 (1.School of Mathematics,Wenshan University,Wenshan,Yunnan 663000,China; 2.School of Mathematics and Statistics,Zhengzhou Normal University,Zhengzhou,Henan 450044,China) The parameterβ(0≤β<0.5)isintroducedbasedontheclassicalroughsetmodelinthispaper.obtainingthevariableprecisionroughsetmodel.Andthepaperdiscussessomepropertiesofupperandlowerapproximationoperatorsinvariableprecisionroughsetmodel.Withtheincreaseofclassificationerror,positivefieldandnegativefieldareexpanded,butboundaryshrinking.Atthesametimethroughaclassicexample,itillustratesthevariableprecisioncomparedwiththeclassicalroughsetmodelandit’simprovedaccuracyofroughsetmodel. rough set;variable precision rough sets;approximate operator 国家自然科学基金资助项目(11361074);云南省科技厅应用基础研究青年项目(2013FD052);文山学院科研基金项目:“曲率和挠率相关问题的研究”(14WSY01);文山学院重点学科数学建设项目(12WSXK01);文山学院高等代数精品课程 黄卫华(1979-),女,河南中牟人,文山学院数学学院教师,硕士。 TP A 10.3969/j.issn.1673-1492.2015.04.002 来稿日期:2015-05-142 结 果
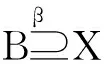

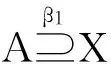


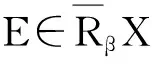

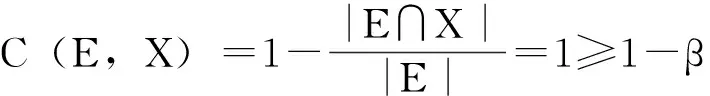
3 实例分析
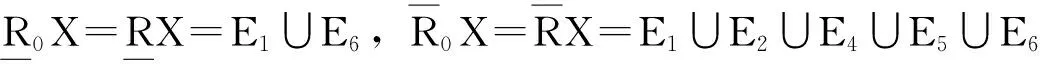
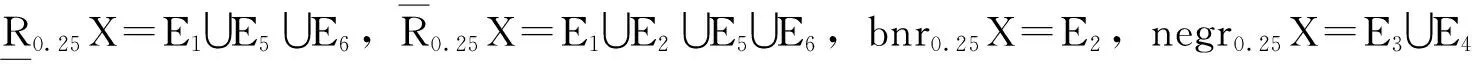
4 结 论

