电力系统无功补偿点的确定及其容量优化

张志强，苗友忠，李笑蓉，赵炜炜，唐晓骏，袁荣湘（.中国电力科学研究院，北京009；.国网冀北电力有限公司经济技术研究院，北京00045；.武汉大学电气工程学院，武汉4007）

电力系统无功补偿点的确定及其容量优化

张志强1，苗友忠2，李笑蓉2，赵炜炜2，唐晓骏1，袁荣湘3
（1.中国电力科学研究院，北京100192；2.国网冀北电力有限公司经济技术研究院，北京100045；3.武汉大学电气工程学院，武汉430072）

电力系统无功优化是一个复杂的非线性组合优化问题，针对该问题提出一种基于奇异值分解理论和改进的粒子群优化算法的无功优化方法。首先对系统潮流计算中雅可比矩阵进行奇异值分解，由奇异值分解理论可以得出矩阵的右奇异向量指标，依据该指标判断电压稳定弱节点，以此作为候选的无功补偿点；然后以有功网损最小为目标函数，构建无功优化数学模型，并提出改进的粒子群优化算法，在算法中引入二次插值算子，增强了算法的局部搜索能力，避免早熟，提高其寻优能力和收敛速度。最后，对IEEE30节点系统进行仿真计算，验证了该方法的有效性。

奇异值分解；二次插值；粒子群算法；无功优化

电力负荷和电网容量的增加使电网的安全经济问题越来越突出，降低网损、提高供电质量成为目前电力部门越来越重视的问题。无功优化作为保证电能质量的重要手段，一直受到研究人员的广泛关注。

电力系统的无功优化包括2个子优化问题，即无功补偿点的确定和无功补偿容量的确定，大多研究一般只针对其中一个方面进行优化，得到的优化结果往往并非最优值。文献[1]利用无功二次精确矩作为指标来确定无功补偿点；文献[2]提出无功裕度的概念，利用节点的无功裕度的值大小候选无功补偿点；文献[3]计算各节点静态能量，以能量信息作为选择无功补偿点依据。以上对无功补偿点优化的同时往往缺少对补偿容量的优化考虑。无功容量的优化方法目前由非线性规划和线性规划等经典优化算法发展到近年的智能优化算法，如模拟退火法、遗传算法和粒子群优化算法等[4-6]。传统的优化方法存在速度慢，收敛性差和求解精度低的缺点，智能优化算法的出现弥补了这些缺点。遗传算法模拟生命进化机制，以模拟自然选择和遗传进化中的繁殖、交配和突变现象为基础发展起来的一种随机搜索技术，有效克服了传统方法在解决复杂问题时的障碍和困难[7]。具有计算时间少、收敛性优良和鲁棒性高的优点。但是遗传算法在求解大规模计算量的问题时容易出现“早熟”现象。粒子群优化算法利用粒子在群体中的合作与竞争的关系，采用“速度-位移”的模型，实现种群在搜索空间内的全局搜索，由于其模型的简单性，因此更加容易实现。每代种群中的个体均具有“自我”学习和向“他人”学习的双重提高优点，故其收敛速度更快，具有更好的精度[8-10]。但是常规的粒子群优化算法容易陷入局部最优，因此本文将二次插值算子引入标准粒子群算法中，提出改进的优化算法。

本文采用先确定无功补偿点再确定无功补偿容量的方法，将潮流计算中雅可比矩阵进行奇异值分解，根据最小奇异值对应的右奇异向量指标候选无功补偿点。建立有功网损最小的目标函数，根据改进的粒子群优化算法，在第个粒子的个体历史最优位置中，任意选择2个作为二次插值的2个值，并结合全局最优位置，产生一个新的个体，若新的个体优于其对应的个体历史最优位置，则进行替换，否则保持不变。采用分段调整加速因子的方法，改变搜索算法不同阶段跟随“自身经验”和“群体经验”的权重。通过IEEE30节点系统进行仿真，验证了该方法的有效性。

1 基于奇异值分解候选无功补偿点

奇异值分解法是在电力系统潮流计算时，将其对应的潮流雅可比矩阵进行奇异值分解，以其最小奇异值δmin以及左右奇异值向量来衡量静态电压稳定性。潮流计算修正方程为

式中，J为雅可比矩阵，是非奇异矩阵，故可将其进行奇异值分解，分解后可得

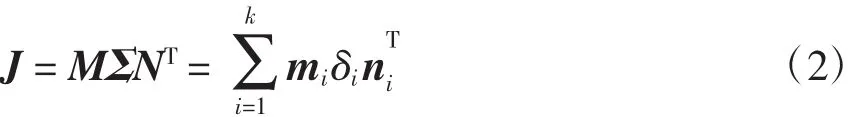
式中：M和N为n维的正交矩阵；k为矩阵J的维数；mi和ni分别为左、右奇异值向量，分别对应矩阵M和N的第i列；δi为奇异值（δ1≥δ2≥…≥δk≥0）；Σ为δi的对角矩阵。根据修正方程可得有功功率和无功功率注入的微小变化引起的矢量（ΔδΔU）的变化，即

如果奇异值δi充分小，则其对应状态变量会变化很大。因此雅克比矩阵的最小奇异值及其左右奇异矢量决定了系统的响应，即

式中：mk为M的最后列，提供了节点功率注入变化的典型模式，根据正交矢量的性质，mTkmk=1；nk为N的最后列，nk中的最大元素对应最灵敏的节点电压幅值，所以可以通过右奇异矢量来判断系统的电压弱节点[11-12]。当系统功率摄动和最小奇异值相关的左奇异矢量相等时，（ΔP，ΔQ）T=mk，故有

本文以雅可比矩阵最小奇异值对应的右奇异矢量中的几个最大值的节点作为无功补偿候选点。

2 基于改进粒子群算法的无功优化

2.1 无功优化数学模型

本文以交流系统网损值最小作为目标函数，其函数表达式为

式中，Ploss为系统有功网损。

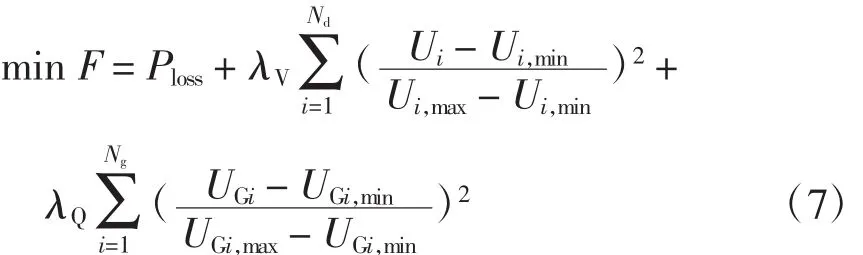
由于负荷节点电压和发电机无功功率为状态变量，可将其通过罚函数的形式引入目标函数，即式中：Ui、Ui，min和Ui，max分别为节点i的电压幅值及其对应的下限值和上限值；UGi、UGi，min和UGi，max分别为发电机i的无功出力及其对应的下限值和上限值；λV、λQ分别为惩罚系数。

2.1.1 等式约束

有功和无功潮流的等式约束方程为

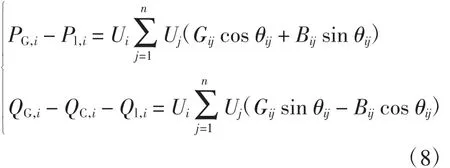
式中：PG，i和QG，i为发电机的有功和无功功率；Pl，i和Ql，i为节点负荷的有功和无功功率；QC，i为补偿节点的无功补偿量；Gij、Bij和θij分别为节点i、j之间的电导、电纳和节点电压相角差。

2.1.2 系统不等式约束

控制变量约束为

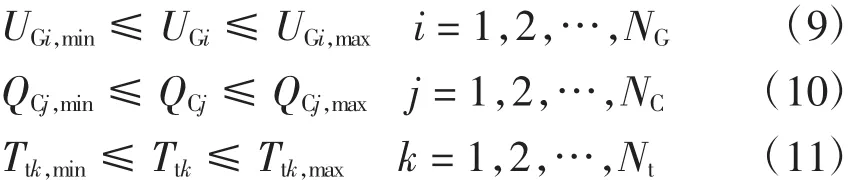
式中：NG、NC和Nt分别为发电机的节点数、无功补偿点数和可调变压器数；QCj为系统补偿节点的无功补偿量，QCj，max和QCj，min为其补偿容量上下限；Ttk、Ttk，max和Ttk，min分别为可调变压器分接头档位及其上下限。

状态变量约束为

式中：Nd为PQ节点数；QGo、QGo，max和QGo，min分别为发电机的无功功率及其上下限；Ulp、Ulp，max和Ulp，min分别为PQ节点电压幅值及其上下限。

2.2 算法研究

2.2.1 标准粒子群优化算法

粒子群优化算法从鸟群觅食的过程中得到启示，并成功发展为一种有效的全局寻优算法，其搜索空间中每个优化问题的解看作为一个“粒子”。若粒子群在D维搜索空间中搜索，种群规模为N，第t代粒子i所处的空间位置为=（i2，…，，i=1，2，…，N，速度为=，…），其个体历史最优位置为（，…，第t代的全局最优位置为P=（，…），则粒子i的速度和位置更新为

式中：c1和c2为学习因子；r1和r2为[0，1]范围内的随机数；ω为惯性权重值，其大小将随迭代的不断进行而改变，由最大值ωmax线性减小到最小值ωmin，即

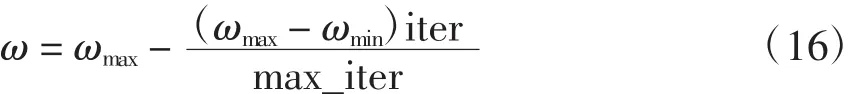
式中：iter为当前迭代数；max_iter为种群最大迭代数。

2.2.2 改进的粒子群优化算法

粒子群优化算法前期的全局搜索能力强，缺点是后期算法的收敛速度将会变慢，影响算法的求解精度，降低了其寻优能力。针对标准粒子群算法的改进，目前已经有诸多研究。文献[13]将混沌优化引入粒子群算法中，并建立黄金分割评判标准，使得算法更有效地搜索到全局最优解；文献[14]将禁忌搜索思想融入粒子群算法中形成混合算法；文献[15]将初始种群随机划分N为个子群，在子群中各自进行寻优计算并共享信息。本文在标准粒子群算法中增加局部搜索策略，在粒子的个体历史最优位置附近进行局部探索，加强PSO算法的局部搜索能力，提高算法的收敛速度。故本文提出一种改进的粒子群优化算法。在D维搜索空间中，其所产生的点为由Pl、Pj和Pg3个点所形成的二次曲面的极小值点，使其具有局部探索能力的功能。本文将二次插值算子引入到粒子群算法中，为了引导个体历史最优位置的局部探索，始终选择群体中的全局最优位置。

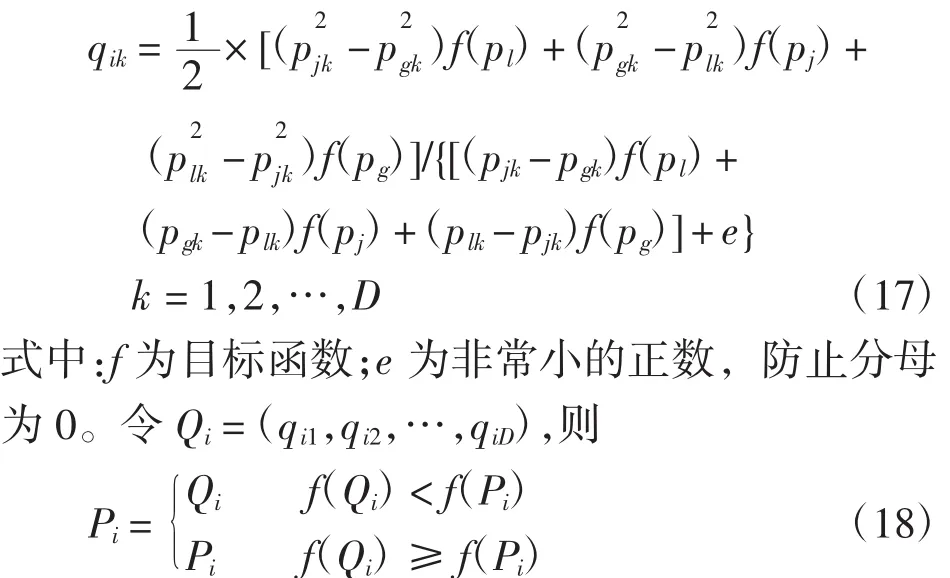
学习因子c1和c2用于协调粒子群中粒子在迭代过程中粒子跟随“自身经验”和“群体经验”的倾向。在基本PSO算法中，一般认为，粒子跟随个体极值和全局极值的权重相同，忽略了粒子在各个搜索阶段的重点的不同。粒子在搜索前期应主要跟随个体历史极值的运动，在自己的周围空间内进行充分探索，保持自身的快速开发能力，并维持群体的多样性和良好的全局搜索能力。在搜索后期应主要跟随种群历史极值，集中搜索，加快收敛速度，保持全局的搜索精度。故本文采用分段调整加速因子的方法，当t＜Genmax/2时，c1=2，c2=1，粒子主要跟随“自身经验”；当t≥Genmax/2时，c1=1，c2=2，粒子主要跟随“群体经验”。其中，t为当前迭代次数，Genmax为最大迭代次数。c1、c2的具体取值以及分界代数Genmax/2均为定性确定的，在迭代前期，粒子跟随个体极值的权重比较大；在迭代后期，粒子跟随全局极值的权重比较大。

2.3 改进粒子群算法无功优化步骤

改进粒子群算法无功优化步骤如下。

步骤2根据式（17）和式（18）对粒子的个体历史最优位置Pi进行更新，并确定全局最优位置Pg。

步骤3由迭代次数确定加速因子的值，根据式（13）和式（14）更新粒子的速度和位置。

步骤4根据更新后的粒子位置计算粒子的适应度值，确定每个粒子的个体历史最优位置Pi以及种群的当前全局最优位置Pg。

步骤5如果算法达到终止条件，则停止；否则，令t=t+1，转至步骤2。

3 算例仿真

本文选择IEEE30节点系统进行仿真分析，该系统共有6个发电机节点、22个负荷节点和41条支路。系统中发电机节点的编号为1、2、5、8、11、13；可调变压器支路为6-9、6-10、4-12、27-28；发电机节点参数见表1；各节点电压和变压器变比上下限值见表2。由于可调变压器变比为离散变量，粒子群算法是在连续的向量空间中求解，故在进行适应度计算之前要将可调变压器变比向量进行离散化，本文选择其对应距离最近的值。

表1 发电机节点参数Tab.1 Parameters of generator

表2 节点电压和变压器变比上下限Tab.2 Limitations ofbus voltages and transformer taps

将系统潮流雅可比矩阵进行奇异值分解，分解后可得最小奇异值对应的右奇异向量指标从大到小的排序如表3所示。

表3 系统节点右奇异指标排序Tab.3 Ranking ofthe rightsingular vector index

由表3可知，节点26和节点30的右奇异指标值最大，应选为无功补偿点。为验证方法的正确性，分别选择系统原有补偿节点10、节点24和节点26、节点30作为补偿点，进行仿真验证。仿真均采用本文所提出的算法。计算结果如表4所示。

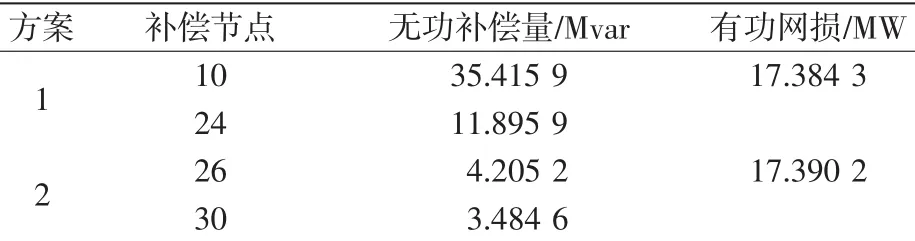
表4 系统无功优化对比结果Tab.4 Comparison ofreactive power optimization

由表4可以看出，方案2的有功网损比方案1的有功网损略高了0.005 9 MW，但其节点的无功补偿量大大低于方案1中的节点无功补偿量。说明本文方法候选的无功补偿弱节点更有效。

为进一步证明改进的粒子群算法的有效性，本文就方案2选择标准粒子群算法和本文算法进行比较；同时为说明改变学习因子的有效性，对c1、c2改进前后进行比较。分别进行20次仿真，结果如表5、表6所示，不同算法的系统网损收敛曲线如图1、图2所示。

表5 算法对比结果Tab.5 Comparison of different algorithms performan M c W e

表6 学习因子调整前后结果对比Tab.6 Comparision of different acceleration coefficient MW

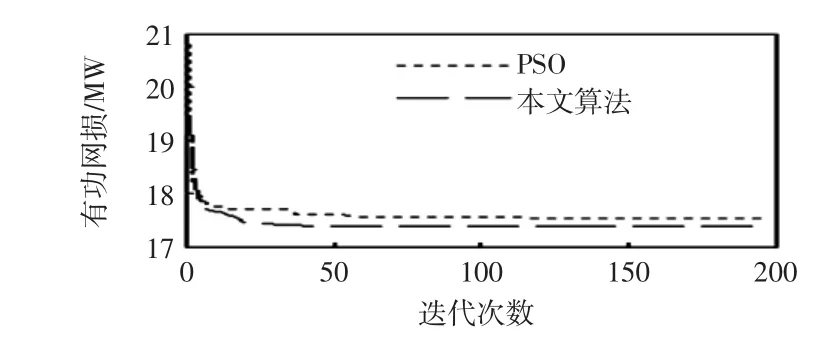
图1 不同算法系统网损收敛曲线Fig.1 Network losses convergence curves via different algorithms

图2 改进学习因子前后系统网损收敛曲线Fig.2 Network losses convergence curves ofdifferentacceleration coefficient

由表5和图1中可以看出，本文改进的粒子群优化算法可以有效减少系统网损，并且具有更好的寻优能力和快速收敛性；表6和图2显示了改进的学习因子对算法性能的提高。

传统的无功优化通常只针对无功优化的2个子问题之一（无功补偿点的选择或者无功容量的确定）进行。无功补偿点确定以后，缺乏对无功容量的优化；或者对无功容量进行了优化，却没有考虑无功补偿点的影响，得到的优化结果往往并非最优。本文同时考虑无功补偿点和无功补偿容量两个方面。从仿真结果可以看出，节点26和节点30为系统弱节点，以此为补偿点可以大大减少节点的无功补偿容量，而对系统网损的增加很小；同时引入二次插值的粒子群优化算法比标准粒子群优化算法收敛速度更快，寻优能力更强。

4 结语

本文首先进行无功补偿点的优化，然后进行无功补偿容量的优化。基于奇异值分解理论，以最小奇异值右向量指标作为选择标准，建立以有功网损最小为目标函数的无功优化模型，改进粒子群优化算法，并将二次插值算子引入优化算法当中，随机选取2个个体历史最优解与全局最优解一起产生新的个体，增强了算法的局部收敛能力。在搜索前期和后期分别选择不同的学习因子，提高了算法的搜索性能。算例仿真结果表明，该方法能够有效减少无功补偿量，改进的粒子群优化算法提高了算法的寻优能力和收敛速度，有效减少了系统的有功网损，提高了电压质量。

[1]矫志宏，蔡中琴，郭志忠（Jiao Zhihong，Cai Zhongqin，Guo Zhizhong）.辐射型配电网无功补偿的精确矩法（Accurate moment method for optimization of capacitors in radial distribution systems）[J].继电器（Relay），2002，30（9）：11-14.

[2]刘传铨，张焰（Liu Chuanquan，Zhang Yan）.电力系统无功补偿点及其补偿容量的确定（Confirmation ofreactive power compensation node and its optimal compensation capacity）[J].电网技术（Power System Technology），2007，31（12）：78-81.

[3]郑武，李华强，陈静，等（Zheng Wu，Li Huaqiang，Chen Jing，etal）.基于静态能量函数法确定交直流系统最优无功补偿点（Optimum reactive compensation position determination based on static energy function for AC/DC power system）[J].电力自动化设备（Electric Power Automation Equipment），2010，30（8）：45-49.

[4]赵昆，耿光飞（Zhao Kun，Geng Guangfei）.基于改进遗传算法的配电网无功优化（Reactive poweroptimization of distribution network based on improved genetic algorithm）[J].电力系统保护与控制（Power System Protection and Control），2011，39（5）：57-62，68.

[5]蔡昌春，丁晓群，王斌（Cai Changchun，Ding Xiaoqun，Wang Bin）.混沌模拟退火算法在无功优化中的应用（Application of chaos simulation annealing in power system reactive optimization）[J].高电压技术（High Voltage Engineering），2008，34（3）：578-582.

[6]李鑫滨，朱庆军（Li Xinbin，Zhu Qingjun）.一种改进粒子群优化算法在多目标无功优化中的应用（Application ofimproved particle swarm optimization algorithm to multiobjective reactive power optimization）[J].电工技术学报（Transactions of China Electrotechnical Society），2010，25（7）：137-143.

[7]杨建军，战红，鲁成杰（Yang Jianjun，Zhan Hong，Lu Chengjie）.配电线路集中无功补偿优化的改进遗传算法（Improved genetic algorithm for centralized reactive power compensation optimization of distribution line）[J].电力系统保护与控制（PowerSystem Protection and Control），2010，38（1）：47-50.

[8]陈前宇，陈维荣，戴朝华，等（Chen Qianyu，Chen Weirong，Dai Chaohua，etal）.基于改进PSO算法的电力系统无功优化（Reactive power optimization based on modified particle swarm optimization algorithm for power system）[J].电力系统及其自动化学报（Proceedings ofthe CSUEPSA），2014，26（2）：8-13，43.

[9]Jarboui B，Damak N，Siarry P，etal.A combinatorialparticle swarm optimization for solving multi-mode resourceconstrained projectscheduling problems[J].Applied Mathematics and Computation，2008，195（1）：299-308.

[10]刘丽军，李捷，蔡金锭（Liu Lijun，Li Jie，Cai Jinding）.基于强引导粒子群与混沌优化的电力系统无功优化（Reactive power optimization based on induction-enhanced particle swarm optimization and chaos search）[J].电力自动化设备（Electric Power Automation Equipment），2010，30（4）：71-75.

[11]向洁，蔡静谊，刘小林，等（Xiang Jie，CaiJingyi，Liu Xiaolin，etal）.基于改进奇异值分解法的电力系统弱节点研究（Research on weak node ofpowersystem based on modified singularvalue decomposition）[J].电气技术（ElectricalEngineering），2012，（8）：55-58.

[12]王林川，于奉振，孙继莆，等（Wang Linchuan，Yu Fengzhen，Sun Jipu，etal）.基于奇异值分解和内点法的交直流电力系统电压稳定裕度研究（Research of AC/DC power system voltage stability margin based on singular value decomposition and interior-point method）[J].电力系统保护与控制（PowerSystem Protection and Control），2011，39（20）：89-92.

[13]汪超，王昕，姚钢，等（Wang Chao，Wang Xin，Yao Gang，etal）.基于黄金分割的混沌粒子群优化算法在配电网无功规划中的应用（Application ofgolden section based chaos particle swarm optimization algorithm in distribution network reactive poweroptimization）[J].电力系统保护与控制（Power System Protection and Control），2012，40（7）：31-36.

[14]曾令全，罗富宝，丁金嫚（Zeng Lingquan，Luo Fubao，Ding Jinman）.禁忌搜索-粒子群算法在无功优化中的应用（Application of particle swarm optimization algorithm integrated with tabu search in reactive power optimization）[J].电网技术（Power System Technology），2011，35（7）：129-133.

[15]刘世成，张建华，刘宗岐（Liu Shicheng，Zhang Jianhua，Liu Zongqi）.并行自适应粒子群算法在电力系统无功优化中的应用（Application of parallel adaptive particle swarm optimization algorithm in reactive power optimization ofpower system）[J].电网技术（Power System Technology），2012，36（1）：108-112.

Location Selection of Reactive Power Compensation and Compensation Capacity Optimization

ZHANG Zhiqiang1，MIAO Youzhong2，LIXiaorong2，ZHAO Weiwei2，TANG Xiaojun1，YUAN Rongxiang3
（1.China Electric Power Research Institute，Beijing 100192，China；2.State Grid JibeiElectric Research Institute，Beijing 100045，China；3.SchoolofElectricalEngineering，Wuhan University，Wuhan 430072，China）

Reactive power optimization is a complicated nonlinear combinatorialoptimization problem in power system. Based on singular value decomposition and improved particle swarm optimization，a novelmethod is proposed to optimizing reactive powerofthe powersystem.Initially，singularvalue decomposition is applied to the Jacobimatrix in the power flow calculation.The rightsingular vector index obtained by singular value decomposition is utilized to identify weak bus as candidate nodes for reactive power compensation.Then，taking minimum active power loss as objective function，a mathematicalmodelfor reactive power optimization is built up，and an improved particle swarm optimization thatintegrates quadratic interpolation is proposed to solve the builtmodel.The new algorithm overcomes the problems of premature convergence frequently in particle swarm optimization，and greatly boosts the searching efficiency and the convergence rate of PSO.Atlast，the simulation resulton IEEE30-bus system indicates thatthe method is feasible and effective.

singular value decomposition；quadratic interpolation；particle swarm optimization；reactive power optimization

TM744

A

1003-8930（2015）03-0092-06

10.3969/j.issn.1003-8930.2015.03.17

张志强（1978—），男，硕士，高级工程师，研究方向为电力系统分析与仿真。Email：zhangzhq@epri.sgcc.com.cn

2014-08-05；

2014-10-20

苗友忠（1976—），男，博士，高级工程师，研究方向为电力系统规划技术。Email：miaoyouzhong@139.com

李笑蓉（1977—），女，硕士，高级工程师，研究方向为电力系统规划技术。Email：lxr_xr@163.com