采用多Agent混沌粒子群算法的配电网重构

唐贤伦，程祥，汪斌全（重庆邮电大学自动化学院，重庆400065）

采用多Agent混沌粒子群算法的配电网重构

唐贤伦，程祥，汪斌全
（重庆邮电大学自动化学院，重庆400065）

针对配电网的辐射状约束条件研究了配电网重构的优化问题，引入破圈法筛选可行解，利用基于多Agent的混沌粒子群算法对筛选后的可行解进行搜索；然后该算法将粒子的群搜索特征与多Agent的智能搜索特征相结合提升算法的搜索效率，并融合混沌局部搜索算法以跳出局部解。以网损为优化目标，分别对33节点和69节点配电网系统进行计算分析，结果表明该算法具有很快的收敛速度，并且对于复杂配电网系统有较好的稳定性与鲁棒性。

配电网重构；破圈法；二进制粒子群；多智能体系统；混沌局部搜索

配电网重构是提高配电网运行效率的一种重要手段，是配电网管理系统的重要组成部分。配电网重构主要是通过控制联络开关和分段开关的闭合状态改变其拓扑结构，影响电网中的潮流分布，起到降低网损、均衡负荷和提高供电电压的作用。

近年来，诸多智能算法如启发式算法[1]、粒子群优化算法[2]、神经网络算法[3]、遗传算法[4]、模拟退火算法[5]以及基于Agent系统的改进算法[6]，应用于电网重构中，都在一定程度上克服了经典数学方法的缺陷，取得了不错的优化效果。其中遗传算法具有良好的全局收敛性，但存在收敛速度较慢及产生不可行解的问题；模拟退火法虽也可以找到全局最优解，但仍存在收敛速度慢的问题；粒子群优化算法由于原理简单易理解，流程清晰易实现，参数简洁易调整以及其在连续优化问题和离散优化问题中都表现良好等特点，已被成功应用于电力系统等复杂优化问题中。但传统的二进制粒子群算法对于需满足辐射状以及无“孤岛”、“环流”拓扑结构特点的配电网还是无法进行深入的局部搜索。

针对上述问题，本文提出了一种新的基于多Agent系统环境结构并通过破圈法筛选可行解的混沌二进制粒子群优化算法。在多MAS环境中，每个Agent均能和邻域的Agent相互竞争合作，而破圈法又能保证电网的拓扑结构特点，二者的结合能够很好地解决收敛速度慢和不可行解的问题，加上混沌局部搜索，使其有更好的全局寻优能力。最后，对IEEE33节点和IEEE69节点系统进行了仿真，仿真结果表明，改进后的算法具有更高的收敛精度、收敛速度和更好的稳定性、鲁棒性。

1 配电网络重构的数学模型

配电网重构是在满足配电系统稳定运行的约束条件下，通过控制开关闭合状态组合使配电网的某个或某几个目标值达到最佳。本文是以降低网损为目标，其数学模型为

式中：F为重构优化目标函数；i为支路序号；ki为对应支路的闭合状态；Ri为对应支路的电阻；Pi和Qi分别为支路末端的有功功率和无功功率；Vi为支路的末端电压。

在重构过程中，配电网还需同时满足如下的一系列约束条件。

（1）潮流约束为

式中：A为节点-支路关联矩阵；i为所有支路的复电流矢量；I为所有节点的复电流注入矢量。

（2）支路容量约束为

式中：Ib为对应支路允许流经的电流；|Ib|max为对应支路允许流经电流幅值的最大值。

（3）配电网节点电压约束为

式中，Vi、Vi，max、Vi，min分别为节点i的电压及其电压上下限。

（4）供电约束为重构后的配电网应该无孤岛、无环流现象。

（5）网络拓扑约束为重构后的配电网必须呈辐射状。

对于适应度函数的计算，采用前推回代潮流计算法计算网络损耗[7]，但由于在网络重构过程中，配电网的拓扑结构不断地变化，而传统的潮流算法只能针对已知拓扑结构进行计算，所以本文在计算适应值时结合了广度搜索[8]的方法，较好地处理了电网拓扑结构变化带来的潮流计算问题。

2 二进制粒子群算法

普通的粒子群算法是人们对鸟类捕食行为的模拟，广泛应用于连续空间的优化问题。为了解决离散空间的优化问题，Kennedy等[9]提出了二进制PSO算法。

在该算法中，粒子位置的每一维分量被限制为0和1，分别对应着配电网中支路开关的断开和闭合。假设在一个D维的搜索空间中，第i粒子的位置为Xid，飞行速度为vid，各粒子经过的最好位置记为Pbest，群体所有粒子经过最好位置记为Gbest。其中，速度应理解为概率，即位置分量取0或1的概率。通过Sigmoid函数将粒子的速度转换到区间[0，1]上，速度和位置更新公式为

3 破圈法搜索可行解

配电网重构不同于单纯的离散问题，重构的配电网必须满足电力系统运行的基本要求，如无孤岛、无环流、电网拓扑结构呈辐射状等。单纯的二进制粒子群算法不能够使其满足这些条件，从而会带来大量的不可行解，使得算法收敛过慢，易陷入局部最优解等。

依据图论可知，如果保证辐射状，那么网络中闭合的支路数=有效节点数-1，因此，对于含有环网的电网，在进行重构时打开的支路数等于基本回路数。

IEEE33节点配电网系统示意如图1所示。将依次从回路中删边得到其生成树的方法称为破圈法。33节点破圈法的计算过程如下。

首先确定基本回路：

R1=[2，19，20，21，8，7，6，5，4，3]；

R2=[21，22，12，11，10，9，8]；

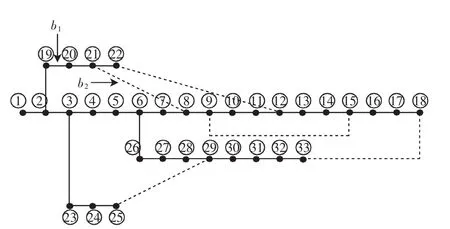
图1 IEEE33节点配电网系统Fig.1 IEEE 33-bus system

R3=[9，10，11，12，13，14，15]；

R4=[6，7，8，9，15，16，17，18，33，32，31，30，29，28，27，26]；

R5=[3，4，5，6，26，27，28，29，25，24，23]。

然后计算各支路对应速度的Sigmoid值，选择Sigmoid值最小的支路打开，会出现2种情况，如图2所示。

（1）选中的支路只属于一个回路，如图1的支路b1，该支路仅属于回路R1，打开它对其他回路没有影响。所以对回路组G的更新为

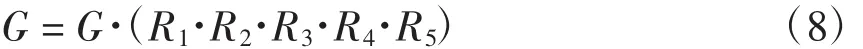
2）选中的支路同属2个基本回路，如图1的支路b2同属回路R1和R2，打开支路后将同时破坏了支路R1和R2，并生成了新的回路Rnew，对新的回路组G的更新为

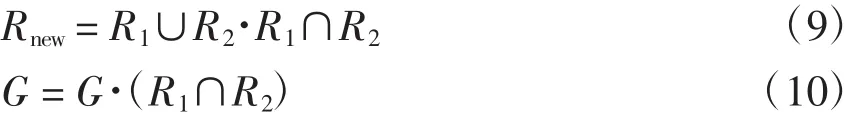
重复上述操作，直至打开的支路数等于网络基本回路数。该方法得到满足辐射状的支路，这样就很好地解决了配电网中的不可行解问题。

4 Agent与多Agent系统

4.1 Agent与多Agent系统

Agent是一种具有感知能力和问题求解能力，又能和系统中其他Agent交互通信，从而完成一个或多个功能目标的软件实体，同时也是一种能够产生推断和决策动作功能的具有智能思维与智能行为的实体，其自身具有自治性、反应性、自发性、社会性和进化性5个基本特征。

多Agent系统是由多个松散耦合的、粗粒度的Agent组成的网络结构。这些Agent在物理上是分散的，其行为是自治的，通过协商、协调和协作，完成复杂的控制任务或者解决复杂的问题。

4.2 Agent所在环境

MAS-PSO设计有一个这样的格子结构环境，它是Agent赖以生存的环境，每个Agent“居住”在该环境中，且被固定在其中的一个格子里，如图2所示。图中每个圆圈表示一个Agent，其坐标表示Agent在环境中的位置，每个Agent有2个参数，也就是DPSO中粒子的位置与速度。

定义环境大小为Lsize×Lsize，即为格子数，相当于DPSO算法中的种群数目。假设Li，j是Agent的格子坐标，其8个邻居被分别定义为

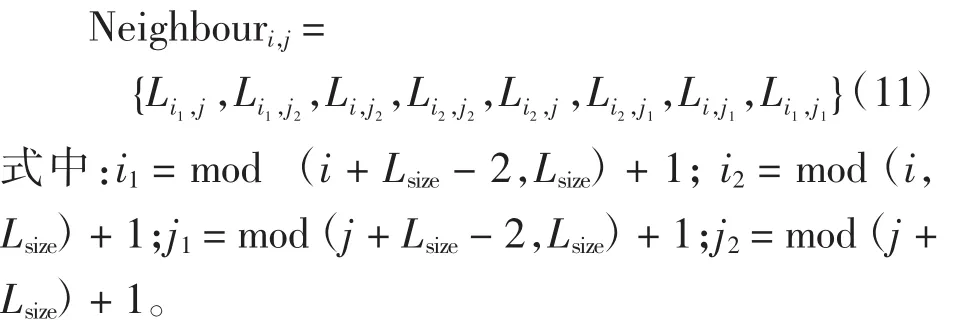
根据定义可知，每个Agent在格子环境中有8个邻居，它们组成该Agent的局部环境。

图2 多智能体拓扑环境Fig.2 Topologicalenvironmentof MAS

4.3 Agent适应值

假设任一粒子即任一个Agent为α，则在多Agent系统中它有一个被优化问题决定的适应值，在网损优化问题中其值由式（1）计算可得。Agentα的目的就是在满足运行条件的情况下，根据自己所处环境做出相应动作，尽可能减小适应值。

4.4 Agent行动策略

各Agent需要感知局部环境的信息以迅速准确地完成任务，通常都有自身的行动策略。各Agent首先与其邻居竞争合作，实现Agent间信息交互的目的。假设对于Agentα，=（，…）；Agentβ为其邻居拥有最小适应值的Agent=（，2，…，）。若Agentα满足

则Agentα为赢家；否则就是输家。

对于赢家Agent，将保持速度和解空间上的位置不变；而对于输家Agent，将被淘汰，并进行速度的更新，产生vnew，k。Agent在解空间上的位置Newi，j由破圈法得到。

新产生的速度更新公式为

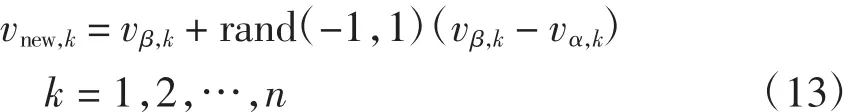
式中，rand（-1，1）为（-1，1）区间内的随机数。若vnew，k＜vk，min，则vnew，k=vk，min；若vnew，k＞vk，max，则vnew，k= vk，max。vk，min是（v1min，v2min，…，vnmin）的下限值，vk，max是（v1max，v2max，…，vnmax）的上限值。从式（13）可知，即便Agentα是劣质粒子，它仍然在保留了自己原本有用信息的基础上充分吸收了最优邻居粒子Agentβ的有益信息，进一步减小了自身的适应值。该策略强调的是对已有信息的进一步挖掘，适合于探索局部空间，可弥补DPSO的缺陷。

5 混沌局部搜索

混沌优化方法利用混沌系统具有的随机性、遍历性和对初值的极端敏感性等特点来实现优化搜索，而且它不要求目标函数具有连续性和可微性的性质，基于混沌的搜索技术无疑会比其他搜索更具优越性。

本文将混沌局部搜索融入到优化算法中，对部分经过破圈法筛选的可行解粒子在其周围进行混沌搜索。在算法中，为保持种群多样性，加强搜索的分散性，保留一定数量优秀粒子，将混沌系统融入其中，在粒子的周围进行搜索，更新当前粒子的最优解，以此帮助惰性粒子逃离局部极小点，提高Agent群体的学习能力以及算法的收敛精度。

本文采用典型的混沌系统，其模型为

式中，u为控制参量，u=4。其中，P′best应当转化至0～1之间，则系统处于完全混沌状态，这样可迭代出一个确定的时间序列进行搜索优化。

6 基于破圈的MAS-CPSO算法

6.1 算法概述

PSO（particle swarm optimization）算法和MAS从本质上讲都是松散耦合的“智能群”结构，这种群所体现出来的智能性来源于两方面：一是群内部精巧的信息流反馈结构带来的群规模效应；二是群中的粒子自身的智能性通过群体凸显出来。PSO算法的智能性主要来自第1个方面，众多的粒子群改进算法也主要集中在此方面；MAS则注重单个智能体智能结构的确立，因此多数MAS结构的改进主要体现在第2方面。传统的DPSO算法在整个搜索过程中处于一种无规则的发散状态，粒子发散性较强，尤其到达进化后期粒子种群局部搜索能力较弱[10]，MAS并发协作式结构需借助其他算法才能更好体现。

本文提出的基于破圈法的MAS-CPSO（particle swarm optimization ofthe chaos-local-search based on multi-agentsystem）结合了MAS的主要结构功能、粒子群的快速迭代特征、混沌系统的遍历性和随机性以及破圈法保证电网的辐射状，有针对性地解决了电网重构的迭代速度慢和不可行解的问题。

6.2 算法步骤

步骤1构造MAS格子环境，在该多Agent环境中初始化设置粒子群的规模、最大允许迭代次数或适应度误差限、惯性权值、学习因子等参数；并初始化粒子在解空间中的速度；

步骤2根据速度利用破圈法得到粒子的可行解，并计算各自的适应值；

步骤3根据行动策略式（12）、式（13），各Agent与8个邻居进行竞争与合作，并更新各自适应值；

步骤4根据PSO迭代式（5）、式（6）更新各Agent粒子在解空间中的速度和位置；

步骤5计算各个粒子的适应值，选取20%优秀的粒子进行混沌局部搜索并更新各粒子的个体极值和群体的全局极值；

步骤6若算法未满足优化结束条件，转向步骤3，否则转向步骤7；

步骤7输出最优解。

7 仿真结果分析

设定粒子群规模为49，惯性因子初始值为0.8，学习因子c1、c2均为2.0，速度上下限vmax、vmin分别为4.0、-4.0；最大迭代次数为50。

1）算例1

本算例采用33节点配电网系统，该系统是一个额定电压为12.66 kV的配电系统，包含37个支路，5个联络开关，其基准容量为10 MVA，总负荷为3 715 kW+j2 300 kvar。

为比较算法的优劣性，分别对算法PSO、MASPSO和MAS-CPSO进行实验仿真，结果如图3所示，表1为33节点配电网重构前后本文算法与其他文献的对比结果，表2为不同算法50次实验的寻优性能比较结果。

由图4可见，在33节点配电网系统中PSO算法虽然收敛迅速，但PSO算法的搜索过程是处于无规则状态，粒子发散性较强，搜索后期粒子的局部搜索能力较弱容易陷入局部最优，这也导致表2中显示的寻优成功率较低的情况发生；MAS-CPSO和MAS-PSO的优势较为明显，均能够以较快的速度收敛并且脱离局部最优，找到全局最优解，从表2可知两者平均迭代次数较PSO高，这主要是因为加入的多Agent系统使粒子还需与邻居竞争合作，加大了粒子的发散性，减缓迭代进程，但却避免了粒子陷入局部最优解。表2中这两种算法在50次实验中寻优成功率高达100%就表明了这两种算法的优越性。MAS-CPSO相对MAS-PSO迭代次数较少，但优势不明显，这主要是由于33节点配电网系统较为简单，混沌搜索的遍历性优点未得到体现。

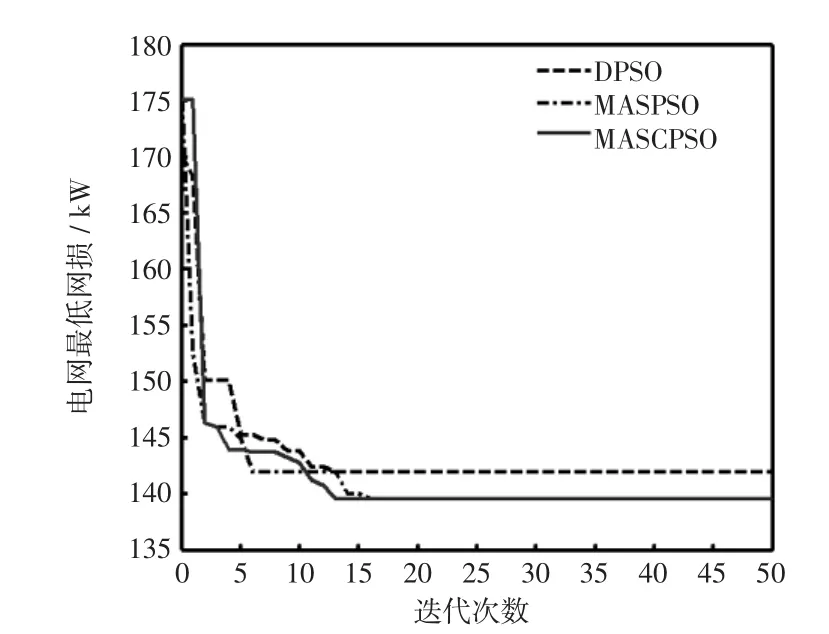
图3 IEEE33节点的收敛比较Fig.3 Convergence comparison of IEEE 33 bus

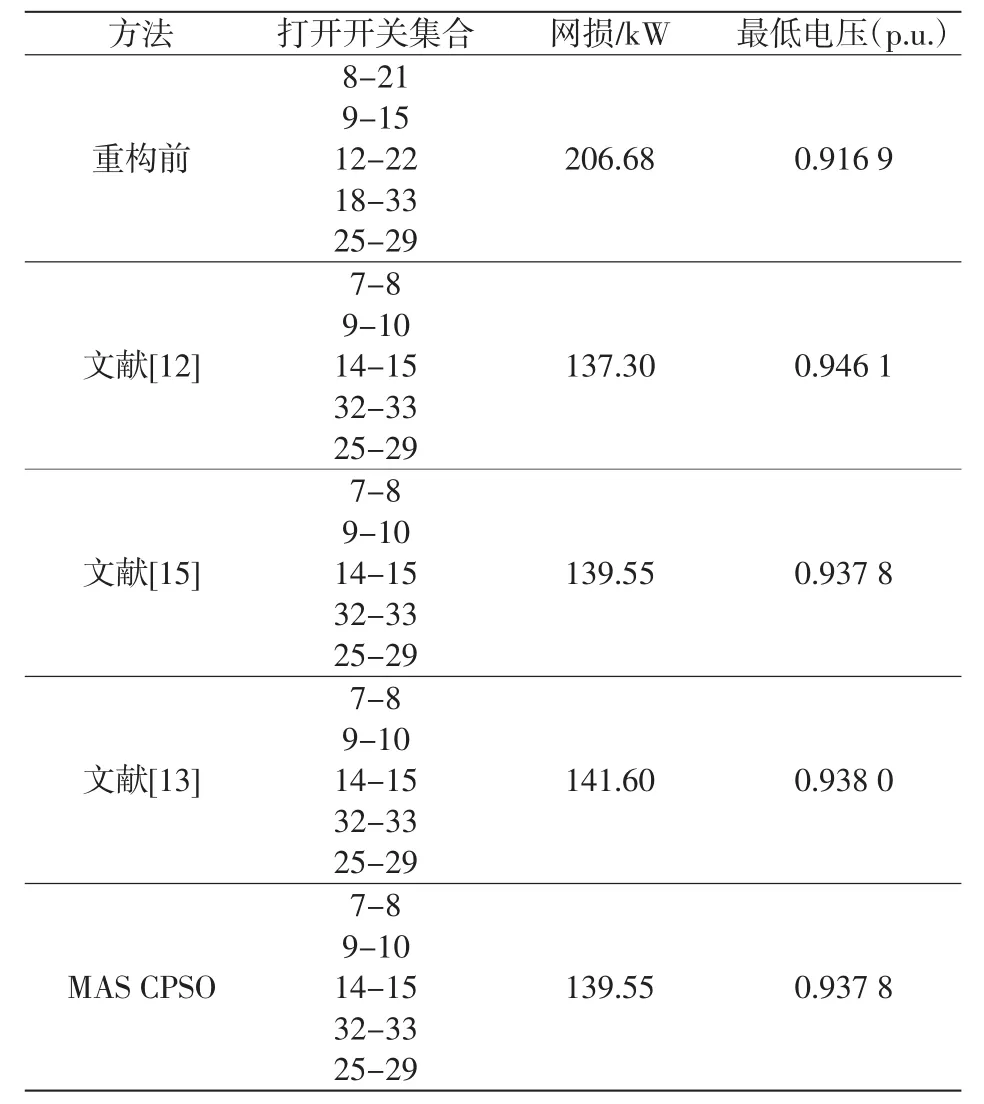
表1 配电网络重构前后比较（33节点）Tab.1 Comparison of distribution network before and after reconfiguration（33-bus）

表2 33节点寻优性能比较Tab.2 Optima searching performance comparisons for 33-bus

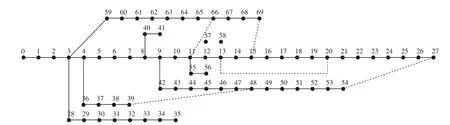
图4 PG&E 69节点配电网系统Fig.4 PG&E 69-bus distribution network

2）算例2

本算例采用美国PG&E 69节点配电网系统，如图4所示。该系统有74条支路，5个联络开关，基准电压为12.66 kV，基准容量为10 MV·A，总负荷为3 802.2 kW+j2 694.6 kvar。

同样分别用DPSO、MAS-PSO和MAS-CPSO算法对69节点系统进行仿真，结果如图5所示，表3是69节点配电网重构前后本文算法与其他文献的结果对比，表4为50次实验中不同算法的寻优性能比较。

从69节点系统的仿真结果可看出，MAS-CPSO比MAS-PSO更加稳定，MAS-PSO出现了局部最优值，而MAS-CPSO的寻优成功率仍然为100%，其原因在于混沌局部搜索在粒子的周围进行搜索，加强了粒子搜索的分散性，以此帮助惰性粒子逃离局部极小点，使该算法与MAS-PSO相比寻优能力进一步提升。由图5可以看出，该算法具有很好的收敛性，脱离局部最优解的能力也很强，由表4的统计结果可知，随着系统的复杂度增加，MASPSO已经出现了2个局部最优解，寻优率为96%。由此，加入混沌局部搜索的MAS-CPSO对于复杂的配电网系统都具有很好的稳定性和收敛效果。

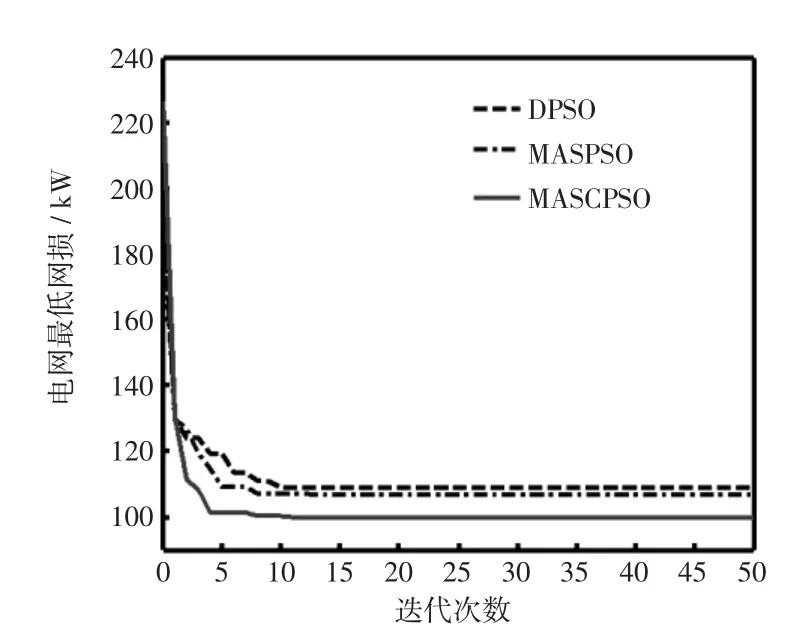
图5 69节点的算法收敛比较Fig.5 Convergence comparison of69-bus

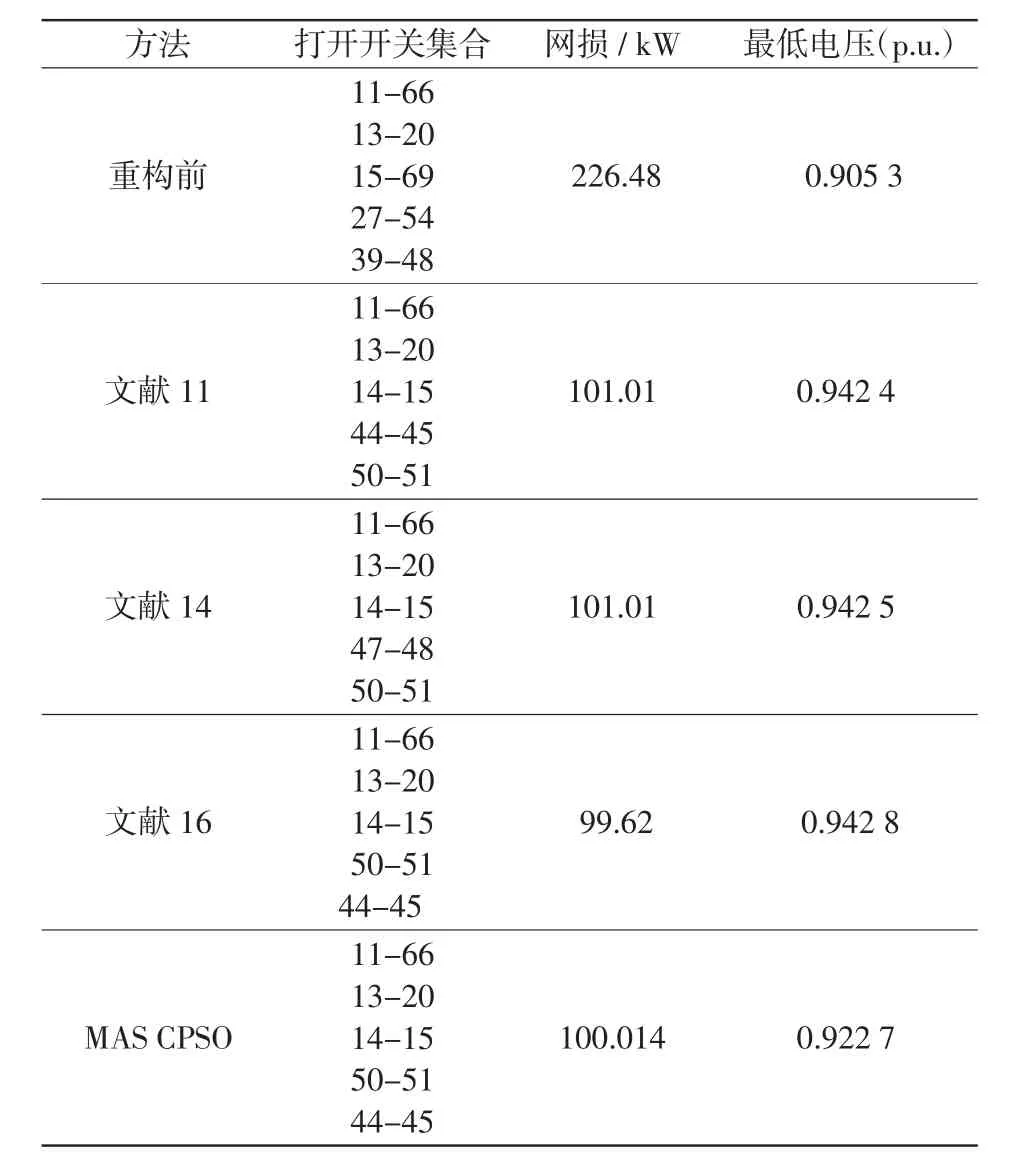
表3 配电网络重构前后比较（69节点）Tab.3 Comparison ofdistribution before and after reconfiguration（69-bus）

表4 69节点系统不同算法寻优性能比较Tab.4 Optima searching performance comparison of different algorithms for 69-bus system

8 结语

本文针对配电网重构问题，提出了基于多Agent系统结构的混沌粒子群优化算法。首先利用破圈法筛选可行解，保证满足配电网的辐射状及其他结构特点；其次利用多智能体的信息交互性将二进制粒子群与多智能体结合，大大地提高了算法的收敛性和优越性。同时考虑到对于复杂的配电网系统，算法必须具有一定的稳定性，所以融入混沌局部搜索提高算法的稳定性，并利用该算法对33节点和69节点配电网进行仿真，其结果表明，基于破圈法的MAS-CPSO是一种解决配电网重构的有效方法，同时对于类似的离散优化或多目标的工程问题，该算法提供了很好的解决手段。

[1]Kargar A，Maleki V.Reconfiguration of distribution systems with distributed generators based on imperialistcompetitive algorithm[C]//17th Conference on Electrical Power Distribution Networks.Tehran，Iran：2012.

[2]Sawa T.Radial network reconfiguration method in distribution system using mutation particle swarm optimization [C]//IEEE Power Tech.Bucharest，Romania：2009.

[3]Salazar H，Gallego R，Romero R.Artificialneuralnetworks and clustering techniques applied in the reconfiguration of distribution systems[J].IEEE Trans on Power Delivery，2006，21（3）：1735-1742.

[4]梁勇，张焰，候志俭（Liang Yong，Zhang Yan，Hou Zhijian）．遗传算法在配电网重构中的应用（Application of the genetic algorithm in the distribution reconfiguration for loss reduction）[J].电力系统及其自动化学报（Proceedings ofthe CSU-EPSA），1998，10（4）：29-34.

[5]陈曦，程浩忠，戴岭，等（Chen Xi，Cheng Haozhong，Dai Ling，etal）．邻域退火粒子群算法在配电网重构中的应用（Application ofsimulated annealing particle swarm optimization algorithm in reconfiguration ofdistribution networks）[J].高电压技术（High Voltage Engineering），2008，34（1）：148-153.

[6]李传健，刘前进（Li Chuanjian，Liu Qianjin）．基于Multiagent和粒子群引导最小生成树的配电网重构算法（A distribution network reconfiguration algorithm based on multi-agent system and minimum spanning tree led by particle swarm optimization）[J].电力系统保护与控制（Power System Protection and Control），2011，39（6）：24-28，33.

[7]王成山，孙充勃，彭克，等（Wang Chengshan，Sun Chongbo，Peng Ke，etal）．微电网交直流混合潮流算法研究（Study on AC-DC hybrid power flow algorithm for microgrid）[J].中国电机工程学报（Proceedings ofthe CSEE），2013，33（4）：8-15.

[8]罗绮，吕林（Luo Qi，LüLin）．一种新的混合优化算法求解配电网重构（A new hybrid optimalalgorithm to solve distribution network reconfiguration）[J].电力系统及其自动化学报（Proceedings ofthe CSU-EPSA），2009，21（1）：89-92.

[9]Kennedy J，Eberhart R.Particle swarm optimization[C]// IEEE InternationalConference on NeuralNetworks.Perth，Australia：1995.

[10]方芹，杨建华，马龙，等（Fang Qin，Yang Jianhua，Ma Long，etal）．基于N-1准则的配电网重构分区评估分析（N-1 security criterion-based analysis and evaluation of partitions on distribution network reconfiguration）[J].电网技术（Power System Technology），2013，37（4）：1091-1094.

[11]卢志刚，杨国良，张晓辉，等（Lu Zhigang，Yang Guoliang，Zhang Xiaohui，etal）．改进二进制粒子群优化算法在配电网络重构中的应用（Reconfiguration of distribution network based on improved particle swarm optimization）[J].电力系统保护与控制（Power System Protection and Control），2009，37（7）：30-34.

[12]周湶，张冠军，李剑，等（Zhou Quan，Zhang Guanjun，Li Jian，etal）．基于化整为零策略和改进二进制差分进化算法的配电网重构（Distribution network reconfiguration based on strategy of breaking up the whole into parts and improved binary differential evolution algorithm）[J].电网技术（Power System Technology），2012，36（3）：197-203.

[13]刘自发，葛少云，余贻鑫，等（Liu Zifa，Ge Shaoyun，Yu Yixin，etal）．一种混合智能算法在配电网络重构中的应用（A hybrid intelligentalgorithm for loss minimum reconfiguration in distribution networks）[J].中国电机工程学报（Proceedings ofthe CSEE），2005，25（15）：73-78.

[14]欧帝宏，陈皓勇，何瑞辉，等（Ou Dihong，Chen Haoyong，He Ruihui，etal）．一种基于解空间划分的配电网最优重构算法（An optimaldistribution network reconfiguration algorithm based on division of solution space）[J].电网技术（Power System Technology），2012，36（3）：140-145.

[15]任怀溥，盛四清，王晓蔚，等（Ren Huaifu，Sheng Siqing，Wang Xiaowei，etal）．基于改进二进制粒子群优化算法的网络重构研究（Research on network reconfiguration based on improved binary particle swarm optimization）[J].电网与清洁能源（PowerSystem and Clean Energy），2011，27（8）：40-43，49.

[16]余健明，张凡（Yu Jianming，Zhang Fan）．基于改进免疫遗传算法的配电网重构（Distribution network reconfiguration based on improved immune genetic algorithm）[J].电网技术（Power System Technology），2009，33（19）：100-105.

Distribution Network Reconfiguration Adopting Chaos Particle Swarm Algorithm of Multi-Agent System

TANG Xianlun，CHENG Xiang，WANG Binquan
（College ofAutomation，Chongqing University ofPosts and Telecommunications，Chongqing 400065，China）

To study the optimization of distribution network reconfiguration，the method of breaking loops is firstly introduced to screen the feasible solutions in consideration ofspoke wise constrained condition，then the particle swarm optimization（PSO）integrated with chaos-local-search（CLS）based on multi-agent system（MAS）is used to conduct further searching.The new algorithm combines the swarm searching feature ofPSO with the intelligentsearching feature of the agent to improve the efficiency of searching.CLS method is involved to leap out the local solutions.Finally，comparative calculation and analysis are conducted on IEEE 33 bus and PG&E 69 bus sample systems.The simulation results show that the MAS-CPSO promises prominent performance not only in the convergence speed but also in the stability and robustness in complex distribution network.

distribution network reconfiguration；breaking loop method；discrete particle swarm optimization（DPSO）；multi-agentsystem（MAS）；chaotic partialsearching

TM726

A

1003-8930（2015）03-0017-07

10.3969/j.issn.1003-8930.2015.03.04

唐贤伦（1977—），男，博士，教授，研究方向为电力系统优化、智能系统。Email：tangxlun@hotmail.com

2013-09-23；

2013-11-22

国家自然科学基金项目（60905066）；重庆市自然科学基金项目（cstc2011jjA1313）

程祥（1991—），男，本科生，研究方向为群体智能、电力系统优化。Email：1148563635@qq.com

汪斌全（1992—），男，本科生，研究方向为智能系统、多Agent系统。Email：1229255894@qq.com