计及用户需求响应的分时电价优化模型

李春燕，许中，马智远（.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400030；.广州供电局，广州44000）

计及用户需求响应的分时电价优化模型

李春燕1，许中2，马智远2
（1.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400030；2.广州供电局，广州440100）

峰谷分时电价是一种有效的价格型需求响应策略，合理的峰谷电价能为用户提供充足有效的价格信号，从而达到削峰填谷的目的。采用需求价格弹性分析用户的用电量随电价的变化情况，从而建立用户的分时电价响应模型。以峰谷差最小为目标，考虑保证用户利益且峰谷电价比在一定范围内等约束条件，建立峰谷分时电价的有约束非线性规划模型。设计分时电价的十进制编码方案，根据生存概率以轮盘赌方式对染色体进行选择复制，以随机概率的方式进行染色体的交叉变异，从而构造相应的遗传算法求解思路。分析该优化分时电价下的需求响应效果，并讨论需求弹性和峰谷时段的改变对优化结果以及需求响应的影响。算例分析表明该模型能有效改善负荷曲线，达到较好的需求响应效果。

需求响应；峰谷分时电价；需求价格弹性；削峰填谷；遗传算法

需求响应DR（demand response）是指用户响应价格信号或激励机制从而改变传统用电方式的行为[1]。在电力市场竞争中引入需求响应，将供应侧和需求侧进行综合资源规划，是适应电力市场发展的必然要求。

需求响应可分为两种类型：激励型DR和价格型DR[2-3]。其中，峰谷分时电价是一种有效的价格型需求响应策略，在电力需求侧管理中起着越来越重要的作用。合理的峰谷电价能从经济上激励用户改变传统用电方式，从而缓解高峰期的用电紧张程度，挖掘低谷期的用电需求，达到削峰填谷的目的[4]。因此，实施峰谷分时电价的关键是合理地确定峰谷时段和峰谷电价水平。

目前基于需求侧的分时电价模型的研究主要集中于用户响应分析[5-13]和时段优化[14-16]等方面。在用户响应建模方面，文献[5]提出负荷转移率的概念，用分段线性函数建立用户对电价的响应度曲线，并采用加权最小二乘拟合法对响应曲线参数进行识别和校正，但未建立相应的分时电价模型；文献[6]基于多智能体技术，考虑了不同用户的用电和响应特点以及用户智能体内部的相互影响建立分时电价模型；文献[7]通过分析不同类型负荷的总体价格弹性、时间-价格弹性建立用户的反映度模型，并用充盈度和舒适度等指标反映用户的满意度，从而建立基于用户响应并考虑用户满意度的分时电价决策模型，但未从经济的角度考虑用户的满意度；文献[8]采用统计学原理，通过分析峰谷电价历史数据建立用户的电价响应矩阵，从用电方式和电费支出两方面衡量用户的满意度，建立电价决策模型；文献[9]基于综合需求响应模型建立实时电价优化模型。以上该模型均未考虑供电公司的利益。文献[10]分析了用户侧峰谷分时电价对供电公司购售电风险的影响，指出实行峰谷分时电价能降低供电公司的购售电风险，且合理确定峰谷电价差率，能够使供电公司的收益和风险达到平衡；文献[11]以电力公司的收益最大化为目标，考虑电力公司是否具有市场力两种情况分别建立售电价格优化模型。

本文基于经济学原理，分析用户对电价的响应，采用需求价格弹性建立用户对峰谷分时电价的响应模型；以调峰为目标，考虑保证用户利益以及峰谷电价比在一定范围内等约束条件，建立峰谷分时电价的非线性有约束优化模型；采用遗传算法进行求解，并讨论了需求弹性和峰谷时段的改变对优化结果以及需求响应的影响。算例分析表明该模型能达到较好的需求响应效果。

1 需求价格弹性

需求价格弹性表示各时段用电量对价格的灵敏度，即在一定时段内电量变化率与电价变化率之比，即

式中：ΔQi和ΔPi分别为i时段的电量和电价变化量；Qi0、Pi0分别为i时段的原始电量和原始电价；Qi、Pi分别为实行峰谷分时电价后i时段的用电量和峰谷分时电价。式（1）表示i时段电量随该时段电价的变化情况，称ρii为该时段的自弹性。根据经济学原理，当电价升高时，用户的需求将减少，因此自弹性为负。

在实际情况中，用户在t时段的用电量不仅与当时电价有关，还受其他时段电价的影响。因此有

式中：i、j为不同的时段；ρij为交叉弹性。当j时段的电价降低时，用户将减少i时段的用电量，从而把i时段的负荷转移一部分到j时段，因此交叉弹性通常为正。

由自弹性和交叉弹性组成的弹性矩阵E为

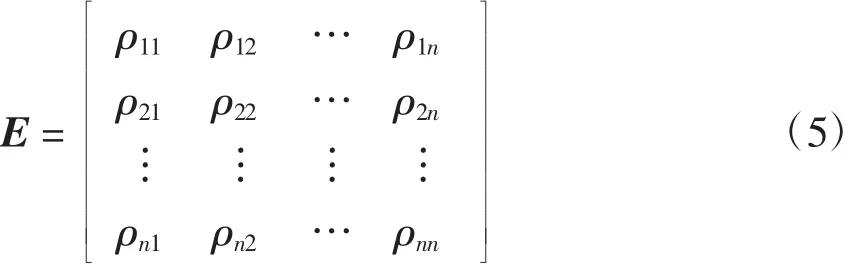
式中，n为时段数，可以根据精度需要采集不同的时段数，n越大，计算的负荷转移就越准确。主对角线元素为自弹性，其弹性值为负；非对角线元素为交叉弹性，其弹性值为正。该弹性矩阵可通过对历史峰谷分时电价机制下的用户用电量进行统计分析获得。

2 基于需求价格弹性的用户响应模型

2.1 单时段用户响应模型

单时段用户响应是指只对当前时段的电价敏感，负荷可以削减但不能转移至其他时段。设在分时电价的引导下，用户在i时段的电量需求由原始需求Qi0变为Qi′，即

设B（Qi′）为用户消耗电量Qi′而获得的效益，则用户的收益S为

常用的效益函数[17]为

式中，Bi0为消耗原始需求Qi0产生的效益。联合式（9）和式（10）可得

进而可得该时段的用户需求为

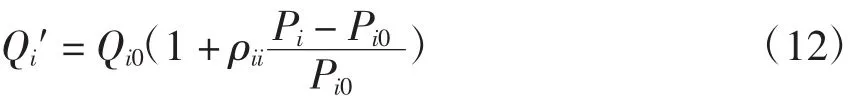
2.2 多时段用户响应模型

多时段用户响应是指对多个时段的电价等激励措施具有敏感性，负荷可以在各时段间转移。根据式（4）的交叉弹性定义，假设需求函数为线性函数，为常数，i，j=1，2，…，24，i≠j，那么实行优化分时电价后i时段的需求为

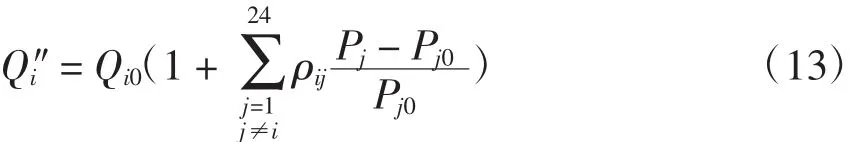
综合式（12）、式（13），则实行分时电价后用户在i时段的综合需求即基于需求价格弹性的综合负荷响应模型为

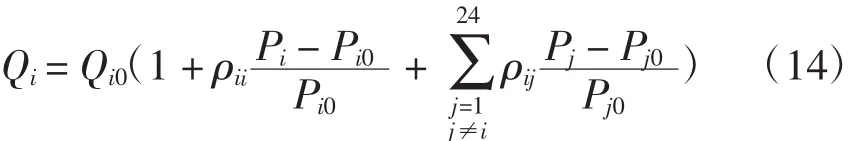
根据原始负荷、原始电价和峰谷分时电价以及需求价格弹性可获得实行分时电价后各时段的电量。

3 分时电价优化模型

由式（14）可知，当已知原始负荷、原始电价和需求弹性时，用户的需求将由峰谷分时电价确定。因此选择峰谷分时电价为决策变量。为实现削峰填谷的目标，可设目标函数为峰谷差最小，即

同时，需要考虑的约束条件如下。

（1）实行峰谷分时电价前后用户的电费支出为

式中，I0和I1分别为实行峰各分时电价前后用户的电费支出。在峰谷分时电价激励下，用户将高峰时段的负荷转移一部分到谷时段以减少其电费的支出，因此需满足

（2）在制定峰谷电价时，峰谷电价比有一定的范围限制，否者将会出现峰谷倒置或响应不足等现象，从而不能达到削峰填谷的目的。因此要求

式中：Pip和Piv分别为峰时段和谷时段电价。在我国，通常峰谷电价比的范围在2～5倍之间较合理。因此本模型中取k1=2，k2=5。

（3）谷时段边际成本约束为

式中，C0为系统在谷时段的边际成本。

4 模型的求解

由式（15）～式（20）构成关于峰谷分时电价的非线性规划模型，采用遗传算法进行求解，算法步骤如下。

步骤1染色体编码及初始化。

采用十进制编码，设

式中，X为峰谷平电价3个决策变量构成的向量，染色体由这3个变量所表示的十进制串构成。通常我国居民电价的取值位于[0，1]之间，可采用保留小数点后3位的小数来表示，因此每个分量都可表示为1个3位的十进制串，每位数由[0，9]之间的随机数构成，从而由3个这样的十进制串依次排列构成1个染色体。

设整数N为群体的规模参数，随机产生N个染色体X（i，0）（i=1，2，…，N），由这些染色体组成的初始群体为

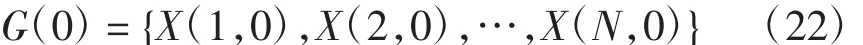
步骤2适应值计算。

以峰谷差的倒数作为适应值函数，计算群体G（k）中每个个体X（i，k）的适应值fi（t X（i，k）），其中k表示进化代数，初始代数k=0；

步骤3选择复制。

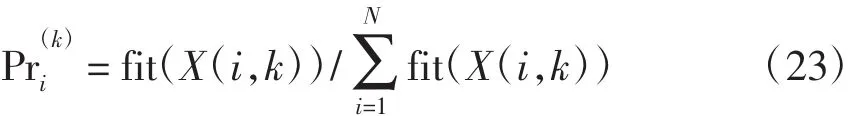
从编号为1的个体开始依次累加各个个体的生存概率，直到满足条件

此时对应第q个个体，因此该个体将被选中复制到下一代。如此反复，选择复制N个个体构成下一代种群G（k+1）。

步骤4杂交。

随机选择2个个体，随机确定交叉位，将2个个体位于该交叉位及其之后的位段相互交换，从而得到新的个体。

步骤5变异。

随机选择串中某位，以变异概率PM改变该位，将该位数值k变为（9-k），完成变异过程。

步骤6停止准则。

循环执行步骤2～步骤5，直到已迭代了预置的代数。以最后一代中适应值最大的个体作为最优解输出。

5 算例分析

以某供电局提供的一组夏季典型日负荷数据为例进行分析，其原始日负荷数据如表1所示。实行分时电价前的平均电价为P0=0.425元/（kW·h），系统在谷时段的边际成本为0.12元/（kW·h）。峰谷平时段的划分如下：峰时段：07∶00—11∶00、17∶00—21∶00；平时段：12∶00—16∶00、22∶00—23∶00；谷时段：24∶00—次日3∶00、3∶00—6∶00。

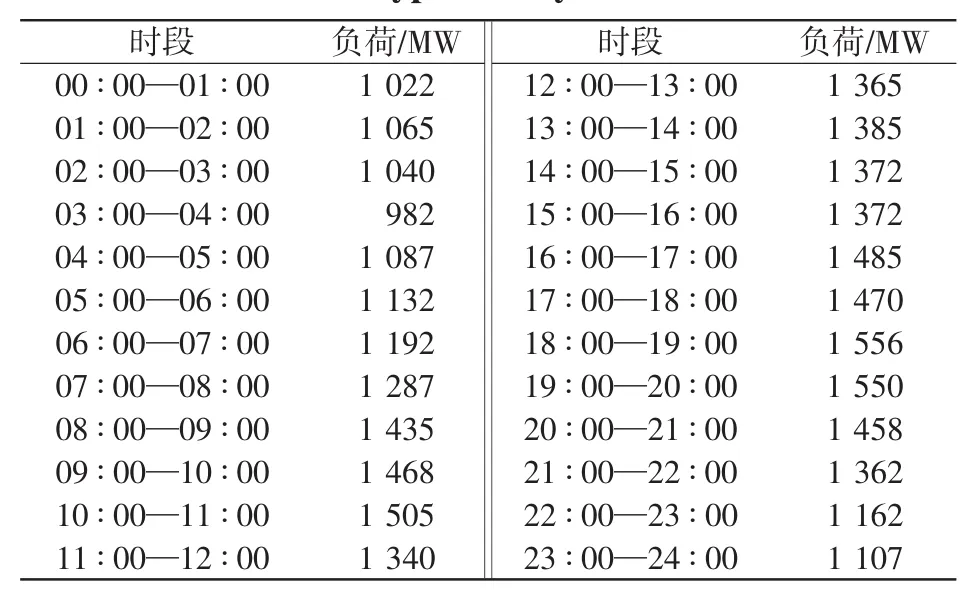
表1 典型的日负荷数据Tab.1 Typicaldaily load data

各个时段用户的需求价格弹性如表2所示。由表可知，各个时段的自弹性均为-0.100，平时段与各时段交叉弹性为0.010，峰时段与各时段的交叉弹性均为0.012，而平时段与峰时段的交叉弹性为0.016。

表2 用户需求价格弹性Tab.2 Price elasticity ofdemand

5.1 优化结果分析

取种群规模为50，交叉概率为0.6，变异概率为0.1，则遗传30代后获得的优化分时电价方案为：峰时段电价为0.592元/（kW·h），平时段电价为0.425元/（kW·h），谷时段电价为0.12元/（kW·h）。优化前后的负荷对比曲线如图1所示。

图1 实行分时电价前后的负荷对比曲线Fig.1 Comparison ofload curves between original price and TOU price

用户按照式（14）对该优化分时电价进行响应，则其需求响应效果如表3所示。

表3 需求响应效果Tab.3 Effectofdemand response

由表3可见，在该优化的分时电价下，通过对用户的响应模型的计算，发现总电量减少了101 MW·h，峰荷减少了29.4 MW，谷荷增加了22.5 MW，峰谷差减少了52 MW，负荷率提高了1.40%，总体性能比原始平均电价都有所提高。

5.2 改变需求价格弹性对优化结果的影响

将表2中的需求弹性放大3倍进行优化分析，则优化的分时电价分别为：峰时段电价为0.615元/（kW·h），平时段电价为0.425元/（kW·h）、谷时段电价为0.123元/（kW·h）。优化前后的负荷对比曲线如图2所示。

图2 改变需求弹性前后的负荷对比曲线Fig.2 Comparison ofload curves between before and after increasing the price elasticity of demand

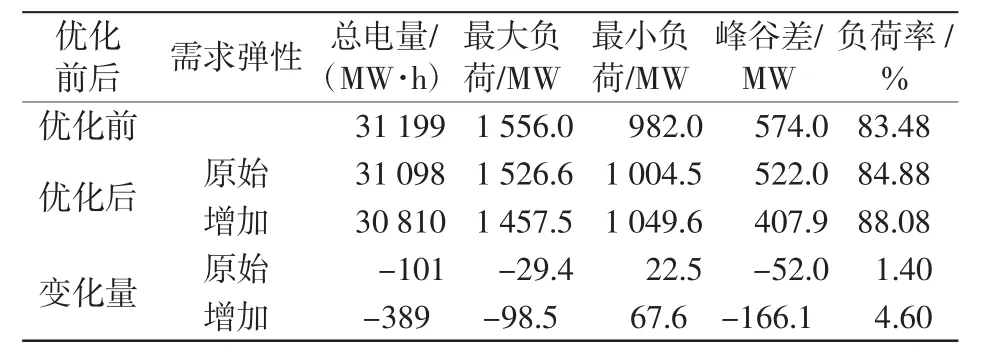
表4 增加需求弹性后的需求响应效果Tab.4 Effect of demand response after increasing the price elasticity of demand

增加需求弹性后的需求响应效果如表4所示。由表可知，增加需求弹性后，总电量减少了389 MWh，峰荷减少了98.5 MW，比原需求弹性下多减少69.1 MW。谷荷增加了67.6 MW，峰谷差减少了166.1 MW，负荷率提高至88.08%，整个负荷曲线比原始负荷曲线更加平坦，削峰填谷的效果更好。

5.3 改变峰平谷时段划分对优化结果的影响

根据原始负荷曲线特点，将峰谷时段划分优化如下：峰时段为9∶00—11∶00，17∶00—21∶00；谷时段为23∶00—次日7∶00；其他时段为平时段。在第5.2节的基础上求解优化模型，获得峰时段电价为0.7元/（kW·h），谷时段电价为0.14元/（kW·h），平时段电价为0.425元/（kW·h）。优化前后的负荷曲线如图3所示。

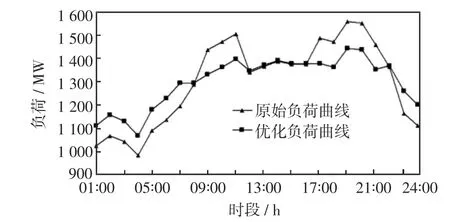
图3 优化时段划分下实行分时电价的负荷曲线Fig.3 Load curves under optimalperiods of TOU price

表5 优化时段下的需求响应效果Tab.5 Effectofdemand response after optimizing the peak and valley periods of TOU price

优化前后的需求响应效果如表5所示。由表可知，优化时段划分比原时段划分的各项性能指标都有所提高。总电量基本保持不变的情况下，峰荷的变化量由98.5 MW增加为114.8 MW，谷荷变化量由67.6 MW增加为81.7 MW，峰谷差变化量由166.1 MW增加为196.5 MW，负荷率由88.08%变为90.09%，整个负荷曲线更加平坦，达到了削峰填谷的效果。

6 结语

本文通过需求价格弹性矩阵建立了用户的响应模型，并基于此以削峰填谷为目标，考虑用电方利益等约束条件，建立了峰谷分时电价优化模型。该模型能够获得优化的分时电价方案，在其引导下用户改变其用电方式，从而通过基于价格的需求响应策略改善负荷曲线。提高用户的需求价格弹性以及对峰谷时段的优化可以使负荷曲线更加平坦，从而达到更好地削峰填谷的作用。

[1]张钦，王锡凡，王建学，等（Zhang Qin，Wang Xifan，Wang Jianxue，etal）.电力市场下需求响应研究综述（Survey ofdemand response research in deregulated electricity markets）[J].电力系统自动化（Automation of Electric Power Systems），2008，32（3）：97-106.

[2]Aalami H A，Moghaddam M P，Yousefi G R.Modeling and prioritizing demand response programs in power markets [J].Electric Power Systems Research，2010，80（4）：426-435.

[3]Mognaddam M P，Abdollahi A，Rashidinejad M.Flexible demand response programs modeling in competitive electricity markets[J].Applied Energy，2011，88（9）：3257-3269.

[4]Wang Jianhui，Bloyd C N，Zhaoguang Hu，et al.Demand response in China[J].Energy，2010，35（4）：1592-1597.

[5]阮文骏，王蓓蓓，李扬，等（Ruan Wenjun，Wang Beibei，Li Yang，etal）．峰谷分时电价下的用户响应行为研究（Customer response behavior in time-of-use price）[J]．电网技术（Power System Technology），2012，36（7）：86-93.

[6]谈金晶，王蓓蓓，李扬（Tan Jinjing，Wang Beibei，Li Yang）．基于多智能体的用户分时电价响应模型（Modeling ofuserresponse to time-of-use price based on multiagenttechnology）[J]．电网技术（Power System Technology），2012，36（2）：257-263.

[7]李晖，康重庆，夏清（Li Hui，Kang Chongqing，Xia Qing）.考虑用户满意度的需求侧管理价格决策模型（Price based decision making for demand side management considering customer satisfaction index）[J]．电网技术（Power System Technology），2004，28（23）：1-6.

[8]丁伟，袁家海，胡兆光（Ding Wei，Yuan Jiahai，Hu Zhaoguang）.基于用户价格响应和满意度的峰谷分时电价决策模型（Time-of-use price decision modelconsidering user reaction and satisfaction index）[J].电力系统自动化（Automation of Electric Power Systems），2005，29（20）：10-14.

[9]Yousefi S，Moghaddam M P，Majd V J.Optimal real time pricing in an agent-based retail market using a comprehensive demand response model[J].Energy，2011，36（9）：5716-5727.

[10]宋艺航，谭忠富，于超，等（Song Yihang，Tan Zhongfu，Yu Chao，etal）.需求侧峰谷分时电价对供电公司购售电风险影响分析模型（Analysis model on the impact of demand-side TOU electricity price on purchasing and selling risk for power supply company）[J].电工技术学报（Transactions of China Electrotechnical Society），2010，25（11）：183-190.

[11]郭联哲，谭忠富，李晓军（Guo Lianzhe，Tan Zhongfu，Li Xiaojun）.基于用户响应下的分时电价优化设计模型与方法（Demand response based model and method for optimaldesign oftime-of-use electricity price）[J].电网技术（Power System Technology），2006，30（5）：24-28.

[12]Yusta J M，Khodr H M，Urdaneta A J.Optimal pricing of default customers in electrical distribution systems：effect behaviorperformance ofdemand response models[J].Electric Power Systems Research，2007，77（5-6）：548-558.

[13]沈欢欢（Shen Huanhuan）.基于需求响应的分时电价研究与分析（Research and Analysis about TOU Based on Demand Response）[D].南京：东南大学电气工程学院（Nanjing：College of Electrical Engineering，Southeast University），2010.

[14]丁宁，吴军基，邹云（Ding Ning，Wu Junji，Zou Yun）.基于DSM的峰谷时段划分及分时电价研究（Research of peak and valley time period partition approach and TOU price on DSM）[J].电力系统自动化（Automation of Electric Power Systems），2001，25（23）：9-12，16.

[15]程瑜，翟娜娜（Cheng Yu，Zhai Nana）.基于用户响应的分时电价时段划分（Electricity price peak and valley periods division based on customer response）[J].电力系统自动化（Automation of Electric Power Systems），2012，36（9）：42-46，53.

[16]葛少云，黄镠，刘洪（Ge Shaoyun，Huang Liu，Liu Hong）.电动汽车有序充电的峰谷电价时段优化（Optimization of peak-valley TOU power price time-period in ordered charging mode ofelectric vehicle）[J].电力系统保护与控制（Power System Protection and Control），2012，40（10）：1-5.

[17]Roos J G，Lane I E.Industrial power demand response analysis for one-portreal-time pricing[J].IEEE Trans on Power Systems，1998，13（1）：159-164.

[18]言大伟，韦钢，陈眩姿，等（Yan Dawei，Wei Gang，Chen Xuanzi，etal）.考虑可中断负荷的微网能量优化（Microgrid energy optimization considering interruptible load）[J].电力系统及其自动化学报（Proceedings ofthe CSUEPSA），2012，24（1）：88-93.

[19]罗耀明，毛李帆，姚建刚，等（Luo Yaoming，Mao Lifan，Yao Jiangang，etal）.电力用户综合能效评估模型（Evaluation model of integrated energy efficiency for power users）[J].电力系统及其自动化学报（Proceedings ofthe CSU-EPSA），2011，23（5）：104-109.

OptimalTime-of-use Electricity Price Model Considering Customer Demand Response

LIChunyan1，XU Zhong2，MA Zhiyuan2
（1.State Key Laboratory ofPower Transmission Equipment&System Security and New Technology，Chongqing University，Chongqing 400030，China；2.Guangzhou Power Supply Bureau，Guangzhou 440100，China）

Time-of-use（TOU）electricity price is an effective price-based demand response strategy，which plays an importantrole on load shifting.The essence ofTOU pricing is to determine its levelso as to provide adequate and effective pricing signal.Firstly，the reaction ofcustomers to TOU electricity price is analyzed based on the price-based demand response in this paper.Then the response modelis established via the price elasticity of demand.By setting the load shifting as the objectand taking into consideration some restrictions such as ensuring both powersupply companies and customers obtain profit and making the TOU price rate restricted in a range，so the optimal TOU pricing model is established in this paper.The model is solved by the genetic algorithm and the influences of elasticity and peak and valley periods on this modelare also discussed.The tests indicate thatthe modelcan improve the load curve and can obtain betterresolution forload shifting effectively.

demand response；time-of-use electricity price；price elasticity of demand；load shifting；genetic algorithm

TM73

A

1003-8930（2015）03-0011-06

10.3969/j.issn.1003-8930.2015.03.03

李春燕（1975—），女，博士，副教授，硕士生导师，研究方向为电力市场、智能电网需求响应以及电力系统分析与计算。Email：lcycqu@cqu.edu.cn许中（1986—），男，硕士，助理工程师，研究方向为智能电网、电能质量分析。Email：348867958@qq.com

2013-08-20；

2013-10-31

国家自然科学基金项目（51247006）；中央高校基本科研业务费项目（CDJZR11150005，CDJRC10150003）

马智远（1987—），男，硕士，助理工程师，研究方向为电气工程。Email：mzy0716@gmail.com