结合矩形窗的EEMD局部放电信号去噪

袁娜，朱永利，梁涵卿（.华北电力大学新能源电力系统国家重点实验室，保定0700；2.中国三峡新能源公司东北分公司，哈尔滨50076；.华北电力大学电气与电子工程学院，保定0700）

结合矩形窗的EEMD局部放电信号去噪

袁娜1，2，朱永利1，梁涵卿3
（1.华北电力大学新能源电力系统国家重点实验室，保定071003；2.中国三峡新能源公司东北分公司，哈尔滨150076；3.华北电力大学电气与电子工程学院，保定071003）

针对现有信号去噪方法的不足，采用总体经验模态分解EEMD（ensemble empirical mode dcomposition）方法对变压器局部放电信号进行消噪，并将其与小波消噪方法进行对比。由于EEMD本身的分解性质及计算机性能的限制，使得对于高采样率长信号的消噪处理变得很困难，故此提出将矩形窗与EEMD算法结合起来进行去噪。研究表明EEMD去噪方法更适合于变压器的局部放电去噪，加矩形窗的EEMD去噪方法通过时间复杂度分析和实验验证，更适合此类局部放电信号的去噪。

局部放电；信号去噪；经验模态分解；矩形窗；小波去噪

局部放电的检测和特征提取对于大型电力变压器在监测和故障诊断具有重要的实际意义，但是局部放电是非常微弱的信号，而现场采集到的局部放电信号往往受到的噪声干扰很大[1]。因此，如何准确地从采集到的信号中提取出局部放电信号，从而进行特征提取是一个很关键的问题。

目前小波去噪方法是一种应用非常广泛的方法[2]，但是小波去噪方法需要选择小波基函数、确定分解层数、选择阈值，参数选择不同，分解方式不同，极大地影响到信号消噪的效果。另外，小波去噪方法不能有效地滤除周期性脉冲干扰，使其在应用于变压器等输变电设备监（检）测信号的分析方面受到限制。经验模态分解EMD（empirical mode decomposition）方法是近年来发展起来的一种新的信号分析方法，这种方法能自适应地将复杂的信号分解成若干阶固有模态函数IMF（intrin-

sic mode function），通过EMD变换实现小波变换的功能，并能够解决波内频率调制的问题，而这是小波变换所不能解决的问题[3]。文献[4]尝试采用EMD对信号进行消噪处理，并验证了其与小波消噪相比的优越性。但EMD方法在分析过程中会产生严重的模态混叠现象，从而影响消噪的结果，为后续分析带来难以预计的影响；文献[5]提出了EEMD的去噪方法，并对其阈值进行了讨论，但没有将EEMD去噪方法与小波去噪方法进行比较，也没有考虑现有信号分析仪器采样率高（数据量大）且EEMD分解运算量大可能诱发的死机问题。

本文在EEMD的基础上，验证了EEMD去噪方法优于小波去噪，并提出加窗的方法对实际高采样率信号（大数据量）进行了去噪分析，减少了对计算机存储和计算资源的要求，从而可避免分析过程中的死机现象。

1 总体经验模态分解理论

1.1 EMD分解原理

Huang等[6]提出，任何复杂的信号均由简单振荡模态信号组成。因此EMD以信号的极值点为集成，首先扫描信号，求出信号所有的极大值点和极小值点；然后利用插值法连接这些点组成上、下包络线，求取其中值形成平均包络线，并用原始信号减去平均包络线得到第1个分量。重复上述步骤直至得到的分量满足IMF信号的定义，每一个IMF在每一个时刻都只有一个单一的频率成分，经过EMD分解之后，任何信号x（t）都可以表示为

式中：IMFi（t）为第i层IMF分量；r（t）为剩余分量；L为分解层数。由此可根据其分解的IMF分量，设计出高通、低通和带通滤波器。

1.2 总体经验模态分解EEMD

由于EMD在降噪过程中存在模态混叠现象，故提出了总体经验模态分解EEMD改进方法[7]。

总体经验模态分解EEMD算法由Flandrin等、Huang等提出，通过加噪声进行辅助分析，其本质是人为添加强度相同但序列不同的白噪声来补充信号的缺失尺度，并对得到的信号进行分解。通过向整个时频空间中加入均匀的白噪声，滤波器组将这个时频空间分割成不同的尺度成分；当均匀噪声作为信号背景加入其中后，不同尺度的信号区域将自动映射到与背景白噪声相应的尺度上去[8]。在此过程中，每个独立的测试都可能会产生非常嘈杂的结果，由于每个独立的测试噪声是不相关的，因此，当添加次数足够多时，噪声将会被消除。文献[9]指出，当添加噪声重复到100次，且强度为0.1～0.3时，能够取得较好的结果；而全体的均值为真正的结果。对每次添加白噪声之后分解得到的每一层IMF取总体平均，即为EEMD的IMF。

对信号进行EMD分解之后得到的每层IMF分量的中心频率均严格保持为前一层IMF中心频率的一半[10]，EEMD的分解也是如此。因此，可以通过选取适当频率范围的IMF以获得不同的滤波效果。

1.3 EEMD去噪

Flandrin指出，白噪声经过EEMD分解以后的各个分量中，第1个分量的能量最大，并且通常最先分解出来的几层IMF分量仅由噪声产生，可以直接滤除。随着分解层数的增加，IMF分量既包含噪声分量又包含有用信号分量，IMF分量需要进行阈值处理，而最后分解得到的IMF分量仅由有用信号产生，可以直接保留。由此得到重构后的信号为

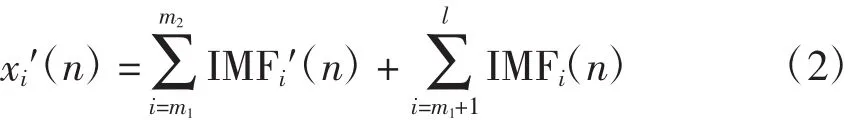
式中，IMF′是经过阈值处理后的IMF分量。最重要的是对IMF分量进行阈值处理，并确定阈值。在阈值的处理方式中，由于硬阈值能够很好地保留信号的细节信息，故选取硬阈值的处理方式，公式为

式中：N为信号的长度；σ为噪声分量的标准差，σ=median（|x）|/0.674 5

从EEMD分解原理来看，每次IMF信号产生都伴随着对信号的一次扫描和对信号所有极大值、极小值的求解。如果信号的点数过多，会导致EEMD分解占用的时间过长，从而产生死机现象。

2 时间复杂度分析

2.1 原始EEMD复杂度分析

时间复杂度通常是考察算法代价的一个关键方面，通常把语句重复执行的次数作为其度量[11-12]。由EEMD分解过程可计算出每一次EEMD分析所占用的时间复杂度T（n），即

式中：a为所添加白噪声的重复次数；n为所分析信号的采样点数，其时间复杂度随着输入信号的采样点数呈对数增长。经过实验验证，当分解次数为100，信号采样点数超过20 000时，EEMD分解速度会明显变慢；当采样点数超过30 000点时，计算机出现了比较多的死机现象。因此本文将矩形窗[13]的思想应用到EEMD去噪中，使得EEMD去噪算法能够适用于高采样率的局部放电信号。

2.2 矩形窗的引入

矩形窗属于时间变量的零次幂窗，其函数为

原信号经过窗函数的截断后变为可以进行EEMD分解的信号。对一个窗内的信号进行EEMD去噪，对下一个矩形窗进行去噪，可以提高去噪的效率，减小计算机的负荷。对每一个去噪后的窗信号进行重构，得到去噪后的信号x′（n）为

式中：M为分窗的个数；xwl（m）为第l个去噪后的窗口信号；m为每个窗的采样点数。

2.3 引入矩形窗后EEMD的复杂度分析

对采样点数为n的信号，假设所分矩形窗数为w，添加白噪声次数为a，则对此信号进行EEMD分解的时间复杂度T（n）为

分窗数越多，每个窗内的采样点数越少，则计算机分解信号的时间越少，有效避免了死机现象。

3 去噪评价系数

为了能够直观地看到去噪效果，采用信噪比SNR（signalnoise ratio）和波形相关系数NCC（normalized correlation coefficient）来描述去噪后的信号和原信号的相似程度[14]，则有

式中：x（n）为原始信号；l为信号长度。SNR和NCC越大，则去噪效果越好。

4 仿真实验分析

对变压器中产生的局部放电进行仿真分析时，通常可采用单指数衰减振荡函数和双指数衰减振荡函数来模拟，其仿真公式为

s1（t）=A1e-（t-t0）/τsin（2πfct）（10）s2（t）=A2[e-1.3（t-t0）/τ-e-2.2（t-t0）/τ]·

sin[2πfc（t-t0）]（11）式中：A为局部放电信号的幅值；t0为局部放电脉冲起始时刻；fc为衰减振荡频率；τ为衰减时间常数。

模拟信号模型参数如表1所示，采样频率为10 MHz，模拟信号如图1所示。

表1 模拟信号模型参数Tab.1 Analog signalmodelparameters

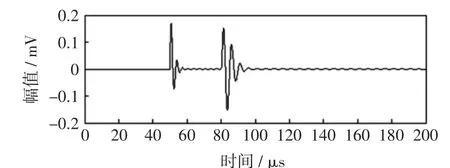
图1 未加噪声原始信号Fig.1 Originalsignalwithout noise

在原信号上加上频率为150 kHz、幅值为0.02 mV的周期脉冲干扰，并附加信噪比为0.5的随机噪声，得到的加噪信号如图2所示。

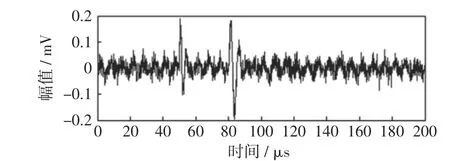
图2 加入脉冲干扰和白噪声的信号Fig.2 Signalwith pulse interference and white noise

分别用小波和EEMD去噪、EEMD分解后得到11层IMF。为了统一，选择小波分解的层数为10层，小波基为‘dB8’小波，得到的小波去噪后的信号和EEMD去噪后的信号如图3所示。

图3 小波和EEMD去噪后信号Fig.3 Denoised results using EEMD and wavelet denoising methods

由图3可以看出，小波去噪基本无法滤除周期脉冲干扰，而EEMD在周期脉冲干扰和白噪声干扰上具有非常良好的滤波特性。

采用信噪比SNR和波形相关系数NCC来说明小波和EEMD去噪的效果。由于在相同信噪比下每次去噪的效果会产生细微的差别，因此对该信号在2种去噪方法下做20组实验取平均值。得到的信噪比和波形相关系数如表2所示。

表2 2种去噪方法评价参数Tab.2 Evaluation parameters of two denoising methods

不同噪声信噪比下，EEMD和小波2种去噪方法的信噪比与波形相关系数如图4所示。

图4 不同信噪比的去噪效果Fig.4 Denoising effectwith different SNR

由图4可以看出，在局部放电信号去噪方面，EEMD去噪方法明显优于小波去噪方法。

5 现场检测信号的去噪分析

实际信号取自某公司在线监测系统采集的数据，系统采样频率为5 MHz，周期信号为20 ms，现场采集到的某个周期的局部放电波形如图5所示。

由图5可见，采集到的信号含有很强的背景噪声，将图中圆圈处的放电脉冲信号放大，见图6。

由图6可以看出，采集到的信号噪声主要是由周围的嘈杂环境及设备带来的，无法直接用来提取特征。周期信号的采样点数是100 000点，若直接进行EEMD分解，将使计算机的负荷加重，在响应一段时间后直接死机，因此需要进行分窗去噪。对每一个窗内的信号进行EEMD去噪，然后对去噪后的窗信号进行重构，窗口大小取为10 000点，程序的平均运行时间是129 s。信号进行分窗去噪以及小波去噪后的波形如图7所示。

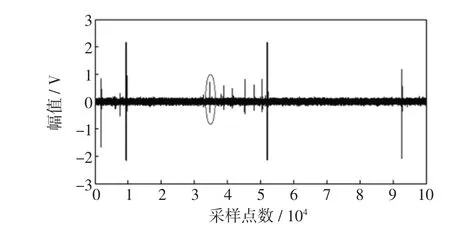
图5 采集到的气隙放电波形Fig.5 Partialdischarge signals from field test

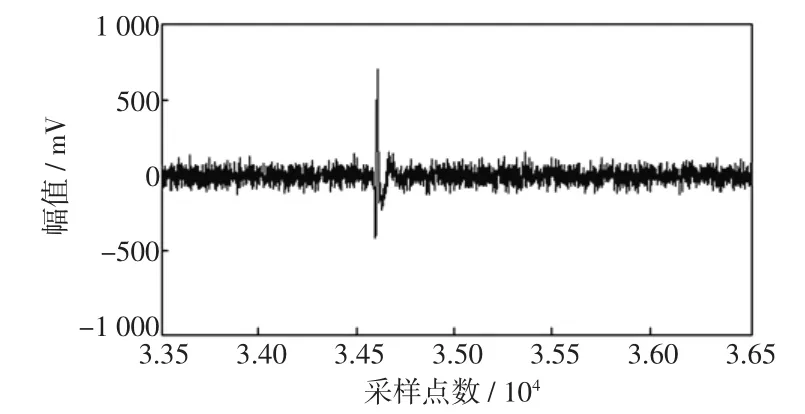
图6 脉冲放大波形Fig.6 Enlarged pulse waveform

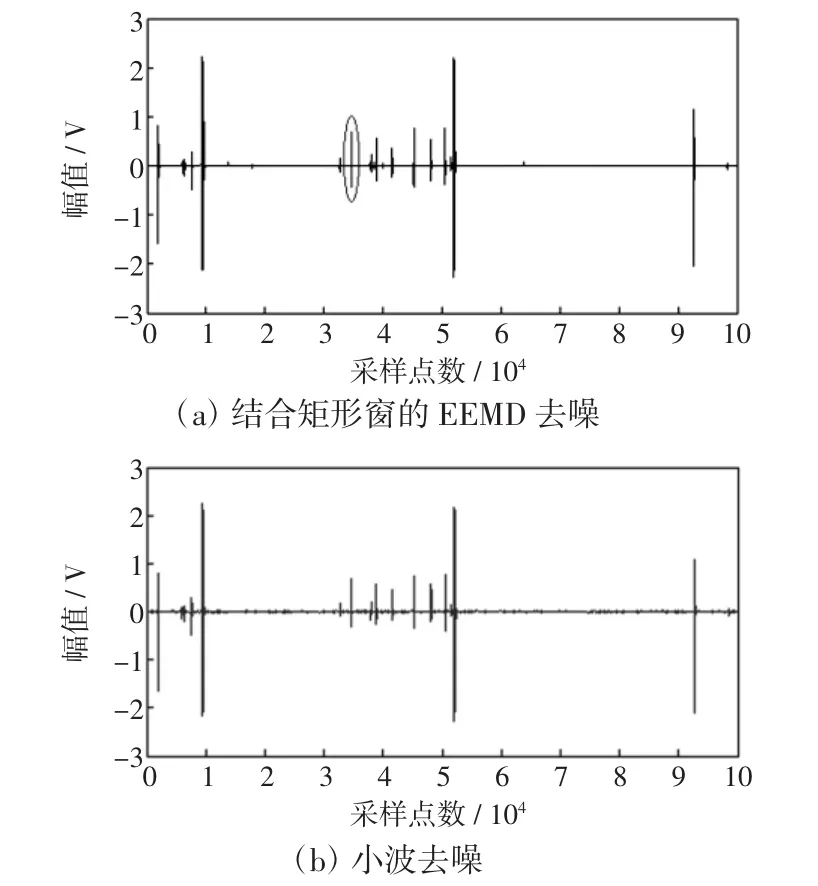
图7 2种方法去噪后的波形Fig.7 Denoised signaluse two methods

放大图7中圆圈处的脉冲信号波形，如图8所示。由图可以看到，小波去噪后的脉冲放大波形并没有很好地滤除噪声，还存在少量的周期脉冲干扰；经过EEMD法去噪后，原信号中的背景噪声已经基本消除，较好地保留了其中的放电脉冲成分。同时，由于采用了分窗的思想，去噪时避免了死机和运行时间过长的现象，在实际现场信号的处理中能节省很多时间，验证了分窗EEMD去噪方法的优越性和有效性。

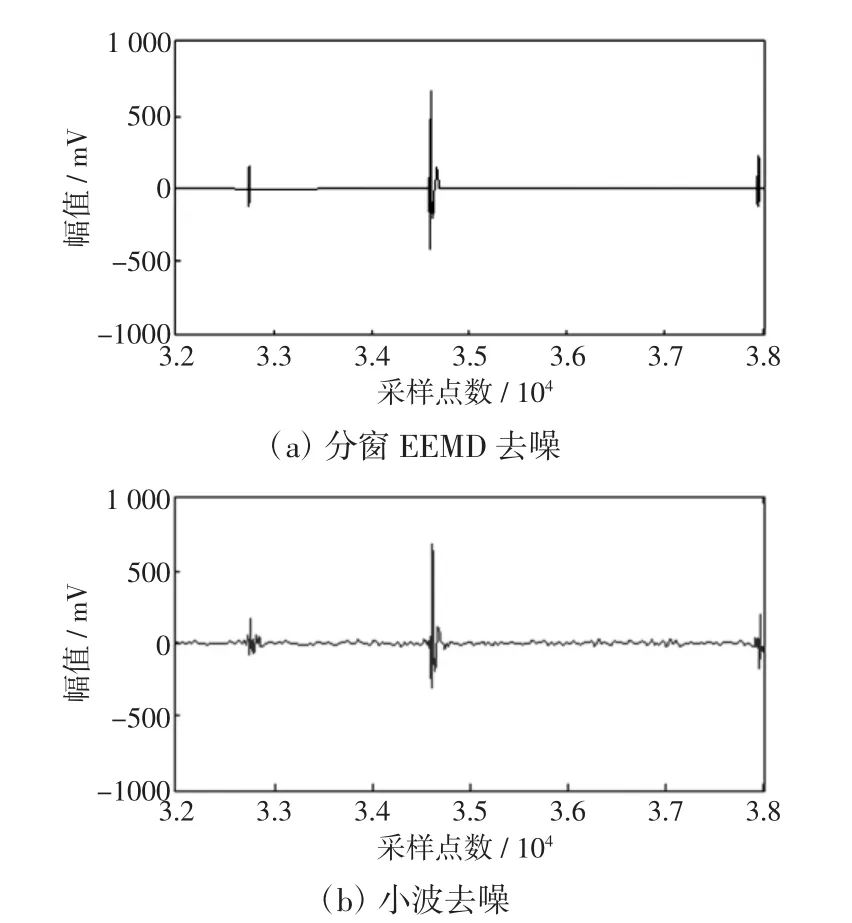
图8 去噪后的脉冲放大波形Fig.8 Enlarged pulse signalafter denoising the noise

6 结论

（1）在局部放电去噪方面，EEMD去噪不仅在参数的选择方面优于小波去噪方法，在去噪效果上也比小波去噪方法好。

（2）采用分窗的办法进行去噪，解决了计算机负荷过重的问题，并且取得了很好的去噪效果。

[1]王晓蓉，杨敏中，严璋（Wang Xiaorong，Yang Minzhong，Yan Zhang）.电力设备局部放电测量中抗干扰研究的现状和展望（Review and prospectofrejecting interference in partialdischarge measurement of power equipment）[J].电网技术（Power System Technology），2000，24（6）：41-45.

[2]柯慧，顾洁（Ke Hui，Gu Jie）.电能质量信号的小波阈值去噪（Waveletthreshold de-noising ofpower system signals）[J].电力系统及其自动化学报（Proceedings ofthe CSU-EPSA），2010，22（2）：103-108.

[3]钱勇，黄成军，陈陈，等（Qian Yong，Huang Chengjun，Chen Chen，etal）.基于经验模态分解的局部放电去噪方法（Denoising of partial discharge based on empirical mode decomposition）[J].电力系统自动化（Automation of Electric Power Systems），2005，29（12）：53-56，60.

[4]孙金宝，朱永利，刘丽轻，等（Sun Jinbao，Zhu Yongli，Liu Liqing，etal）.基于EMD的绝缘子泄漏电流去除噪声研究（Study on de-noising method based on EMD used in insulator leakage current）[J].华北电力大学学报（Journal of North China Electric Power University），2010，37（6）：1-5，22.

[5]姚林朋，郑文栋，钱勇，等（Yao Linpeng，Zheng Wendong，Qian Yong，etal）.基于集合经验模态分解的局部放电信号的窄带干扰抑制（A narrow-band interference suppression method based on EEMD for partialdischarge）[J].电力系统保护与控制（Power System Protection and Control），2011，39（22）：133-139.

[6]Huang N E，Zheng Shen，Long S R．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]．The Royal Society，1998，454（1971）：903-995．

[7]Wu Zhaohua，Huang N E.Ensemble empirical mode decomposition：a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis，2009，1（1）：1-41.

[8]姚林朋，黄成军，钱勇（Yao Linpeng，Huang Chengjun，Qian Yong）.基于EMD的局部放电窄带干扰抑制算法（Empiricalmode decomposition based DSIsuppression algorithm in partialdischarge detection）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（5）：33-38.

[9]Huang N E，Shen S S P.Hilbert-Huang Transform and Its Applications[M].USA：World Scientific Publishing Co.Pte. Ltd.，2005.

[10]Tsolis G，Xenos T D.Signal denoising using empirical mode decomposition and higherorder statistics[J].International Journal of Signal Processing，Image Processing and Pattern Recognition，2011，4（2）：91-106.

[11]谢弗.数据结构与算法分析：C++版[M].北京：电子工业出版社，2010.

[12]王翠茹，袁和金，刘军，等.数据结构（C语言版）[M].北京：中国电力出版社，2006.

[13]胡广书.数字信号处理：理论、算法与实现[M].北京：清华大学出版社，2003.

[14]唐炬，许中荣，孙才新，等（Tang Ju，Xu Zhongrong，Sun Caixin，etal）.应用复小波变换抑制GIS局部放电信号中白噪声干扰的研究（Application of complex wavelet transform to suppress white-noise interference in GIS PD signals）[J].中国电机工程学报（Proceedings of the CSEE），2005，25（16）：30-34.

EEMD De-noising Method Using Rectangular Window

YUAN Na1，2，ZHU Yongli1，LIANG Hanqing3
（1.State Key Laboratory ofAlternate ElectricalPower System with Renewable Energy Sources，North China Electric Power University，Baoding 071003，China；2.China Three Gorges New Energy Corp.Northeastern Branch，Harbin 150076，China；3.Electrical&Electronic Engineering Schoolof North China Electric Power University，Baoding 071003，China）

To deal with the shortcomings of existing denoising methods，the ensemble empirical mode dcomposition（EEMD）de-noising method is applied to denoise the partial discharge signal of the transformer.Which is compared with the conventionalwaveletbased de-noising algorithms.Due to the restrictions of EEMD decomposition and the performance of computer，it becomes very difficult to denoise the high sampling rate signals with long time.Rectangular window is introduced here to be combined with EEMD algorithms to denoise the discharge signals.As a generalresult of the research，EEMD de-noising method is better than wavelet based de-noising.The time complexity analysis and experimentalverification are shown thatwith rectangular window the EEMD de-noising method is more suitable for the high sampling rate signal.

partialdischarge；signaldenoising；empirical mode decomposition（EMD）；rectangularwindow；wavelet based de-noising

TM407

A

1003-8930（2015）03-0054-05

10.3969/j.issn.1003-8930.2015.03.10

袁娜（1987—），女，硕士研究生，研究方向为人工智能。Email：shengshiru@126.com

2013-04-22；

2013-07-31

新能源电力系统国家重点实验室资助项目

朱永利（1963—），男，博士，教授，博士生导师，研究方向为输变电设备网络化监测与信息分析处理。Email：yonglipw@163.com

梁涵卿（1992—），男，本科生，研究方向为电力系统分析。Email：2352993071@qq.com