类SCARA机器人多目标性能优化

张建军，沈爱民，柯辉，杨高炜

（河北工业大学机械工程学院，天津 300130）

类SCARA机器人多目标性能优化

张建军，沈爱民，柯辉，杨高炜

（河北工业大学机械工程学院，天津 300130）

以类SCARA硅片搬运机器人为研究对象，在机器人运动学和动力学的基础上，分析其工作空间、全域条件数、固有频率、误差影响系数各项性能，并针对这4项性能指标进行多目标优化．将机器人机构杆长参数作为设计变量，以工作空间等4项指标作为优化目标，给出杆长约束和相对工作空间系数约束，利用基于BP神经网络算法的多目标遗传算法进行优化计算，采用遗传算法优化神经网络的结构，来提高BP神经网络的预测精度，减少运算时间，最终得到1组最优杆长．采用优化后的机器人机构杆长可以使机器人各项性能指标有较大提高．

性能优化；神经网络；遗传算法；多目标优化

0 前言

并联机器人机构设计是1个困难而复杂的问题，而性能评价指标是设计并联机器人机构的关键问题之一．在设计过程中不可避免地要以一些性能指标作为基础，包括机器人的工作空间、刚度、精度、雅克比矩阵条件数等一些指标[1]．但基于某一性能的优化往往具有局限性，因此依据机器人高速高精度搬运硅片的速度、精度、运动范围等要求，针对机器人的运动学、动力学、精度等性能与评价指标的耦合和制约问题，研究基于运动学参数（即机构几何尺寸）的多目标性能优化，对于机器人性能的提高，具有重要意义．

在机器人性能指标研究上，许多国内外学者做了大量的研究工作，并取得了许多成果．Kumar和Waldron2于八十年代初在这方面做了基础性的工作，提出了搜索工作空间边界的理论和算法．Salisbury[3]等提出了Jacobian矩阵条件数的概念．随后，Angeles[4]等提出了机器人操作器的动力学性能指标．雅克比矩阵条件数是输入速度的放大因子，设计时应控制在比较小的范围内．但是雅克比矩阵条件数依赖于机器人的位姿，只是1个局部指标，为了解决这个问题，Gosselin[5]在1991年提出全域条件数．刘爽、郭希娟[6]等综合利用Jacobian矩阵和Hessian矩阵对一种少自由度并联机构进行速度性能分析，并绘制出性能图谱．而在多目标优化问题上，许多国内外学者也做了大量研究工作．陈静[7]等采用遗传算法对一种两自由度的并联机器人进行了性能优化．李瑞霞[8]使用粒子群算法优化了五自由度的4UPS-UPU并联机器人的全域条件指标和全域梯度指标．Zhang Lufan[9]采用NSGA-II算法优化了宏微观运动平台的连接机构的总重量、关键点最小变形以及第1阶固有频率．Zhang Dan[10]利用粒子群优化算法对土拨鼠机器人的刚度和工作空间进行了优化．Jiman Luo[11]等采用基于Pareto排序的粒子群优化算法（RP-PSO）解决了3-TPS/TP并联机器人的运动学优化．

遗传算法是高效的并行随机搜索最优化方法，而BP神经网络是目前应用最广泛的神经网络模型之一，可以很好地进行非线性函数拟合，将二者结合可以快速有效地进行多目标优化计算．本文采用BP神经网络算法和多目标遗传算法相结合的方法进行类SCARA机器人[12]多目标性能优化．通过对类SCARA机器人的运动学和动力学分析，建立类SCARA机器人多目标性能优化模型，以类SCARA机器人的工作空间、全域条件数、固有频率和误差影响系数4个指标作为优化目标，以机器人的杆长参数作为优化变量，同时给出杆长和相对工作空间系数约束，进行多目标优化，比较优化结果与初始杆长时性能．

1 类SCARA机器人性能优化问题描述

1.1 优化对象

类SCARA机器人是包含3个支链的支链嵌套三自由度并联机器人（如图1所示），由电机1通过滚珠丝杠带动整个动平台沿着Z方向上下移动，电机2经皮带传动带动动平台绕Z轴转动，电机3带动曲柄轴绕Z轴转动，进而使与滑块连接的操作手沿直线导轨移动．该机器人可实现的运动与SCARA机器人类似，所以称之为类SCARA并联机器人．

类SCARA机器人主要应用于硅片自动传输系统，它结合了串联机器人和并联机器人的优点，主要工作为搬运硅片至不同的工位．为了满足工作需要，类SCARA机器人应该要具有适合的工作空间以及较高的速度和精度．

1.2 设计变量

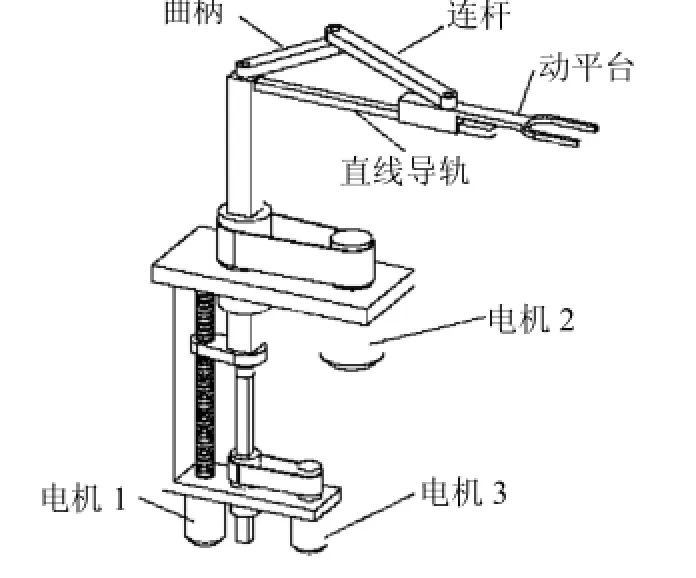
图1 机器人结构示意图Fig.1 Schematic diagram of the structure of robot

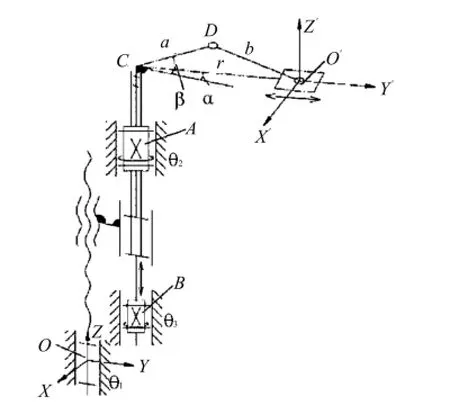
图2 机器人机构简图Fig.2 Robot mechanism sketch

图2为类SCARA机器人机构简图，建立如图所示坐标系，以O XYZ为固定坐标系，以O'X'Y'Z'为动平台坐标系，该机器人的输出包括Z轴方向平移距离z、沿Z轴的转角和点O'距点C的距离r．因此，动平台可以利用柱坐标矢量rzT．输入分别为：O点转动关节的转角1；A点转动关节的转角2和B点转动关节的转角3．该机器人竖直方向的运动与其他2个方向的运动是解耦的，而竖直方向的移动与工作环境和运动范围关系较大，变化范围也比较大，所以这里暂时不予考虑．而曲柄滑块机构的性能主要与曲柄和连杆的杆长有关，其对整个机器人的性能指标影响较大，所以本文主要将曲柄和连杆的杆长参数a，b作为优化参数，且为简便计算，将曲柄和连杆的横截面积视为固定不变的．

1.3 优化目标

该机器人的性能优化目标包括如下4个，其中有2个最小化目标和2个最大化目标，分别是：1）工作空间；2）全域条件数；3）固有频率；4）误差影响系数．

1.3.1 工作空间

本文研究的类SCARA并联机器人有着机构的特殊性，动平台机械手的上下运动是通过滚珠丝杠由伺服电机带动的，动平台上下运动的距离为d．同时动平台是支链嵌套的闭环结构，通过伺服电机的驱动带动机器人末端机械手的圆周回转和径向移动．这使得该机器人的工作空间是1个空心圆柱．

该机器人竖直方向上的运动与动平台的回转和径向进给是解耦的，所以这里可以只考虑动平台平面的工作空间．当给定a，b后，机械手末端参考点的可达空间为以C点为圆心的环形平面区域，区域内外半径由曲柄杆长、连杆杆长和压力角确定，分别为

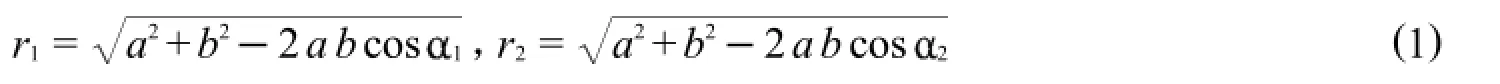
图3给出了工作空间随杆长的变化情况．目标是增大工作空间，所以该机器人性能指标优化问题的第1个优化目标可以写成

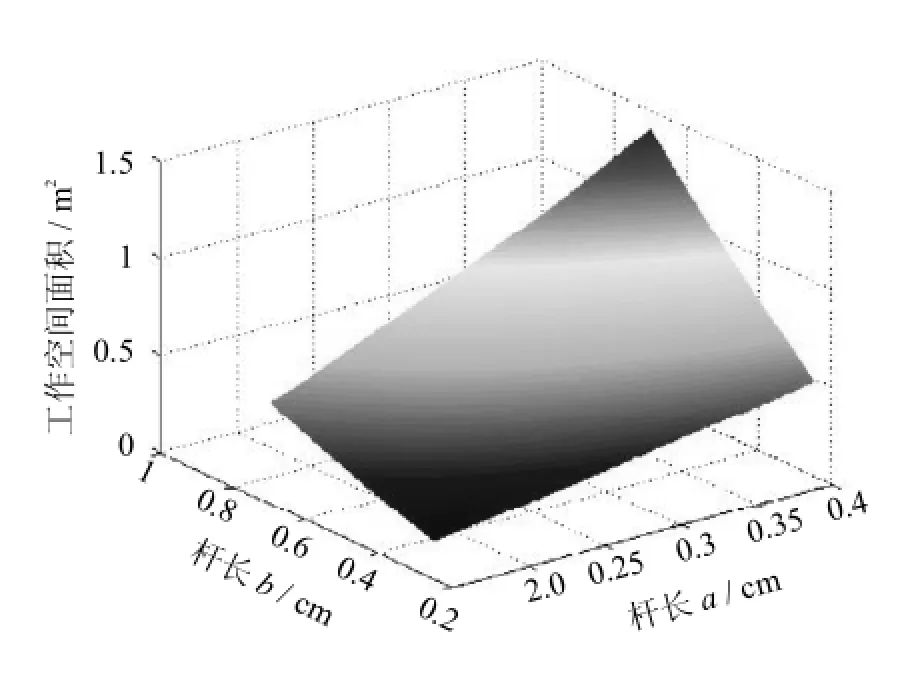
图3 工作空间随杆长变化图Fig.3 Workspace changes with rod length

1.3.2 全域条件数

现在，人们对机器人的精度、速度要求越来越高，如何评价机器人的性能指标已经成为机器人领域1个重要课题．全域条件数作为一种重要的性能指标，是指机器人的运动学和动力学的可逆性，该指标可以反映机器人在整个工作空间内任意方向上的运动和施加力的能力．

雅克比矩阵条件数是输入速度的放大因子，所以设计时应该将其控制在一个较小的范围内．但是雅克比矩阵条件数依赖于机器人的位姿，只是局部指标，为了解决这个问题，Gosselin C在1991年提出全域条件数．

Gosselin C的全域条件数（GCI）可表述如下

根据本机器人运动学分析得到机器人的雅克比矩阵的行列式det，那么类SCARA机器人的工作空间面积为

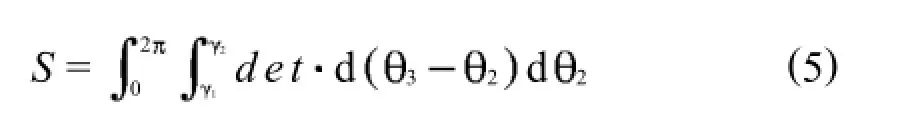
那么全域条件数可以表示为

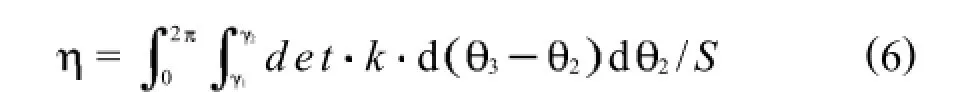
其中：k表示雅克比矩阵条件数，全域条件数随杆长的变化情况如图4所示．

这样类SCARA机器人性能优化问题的第2个目标函数可以写成

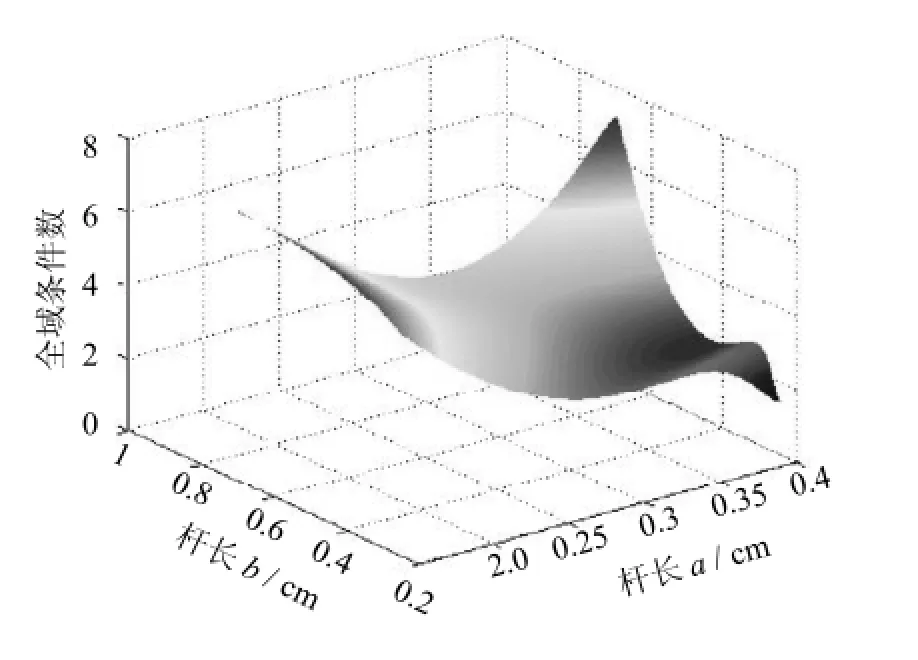
图4 全域条件数随杆长变化图Fig.4 GCI changes w ith rod length

1.3.3 固有频率

研究机械系统动态特性可以提高机械系统的精度，提高机械系统多功能要求．固有频率是振动理论中的重要概念，它反映了振动系统的动力学特性．由于阻尼对机构的固有频率影响比较小，于是可以根据无阻尼自由振动方程得到机构的固有频率．

分析机器人的受力情况，杆a与杆r是原动件，受扭力作用，产生弯曲变形；杆b为连杆，受力分析为二力杆，受拉力作用，产生拉伸变形；机器人动平台发生振动时的变形示意如图5所示．

动平台的动能包含2部分：一部分为构件质心的平动动能；另一部分是构件绕质心的转动动能．系统的势能为系统弹性势能，分别为杆r、杆a和杆b的弹性势能．将系统的动能T和势能V带入拉格朗日方程

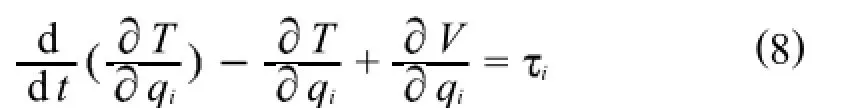
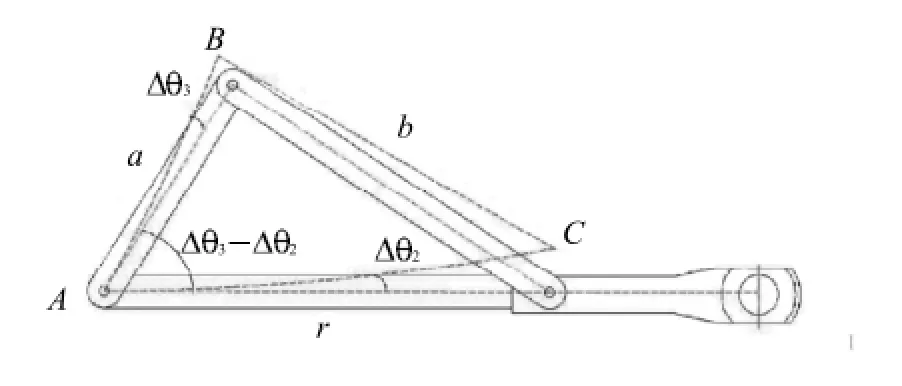
图5 机械臂振动示意图Fig.5 Schem atic diagram of mechanical arm vibration

这样，以32=时的固有频率作为优化目标，当机构位置变化时，固有频率最小的位置点的固有频率提高，那么机构整体的固有频率也会提高，所以该机器人性能优化问题的第3个优化目标函数可以写成

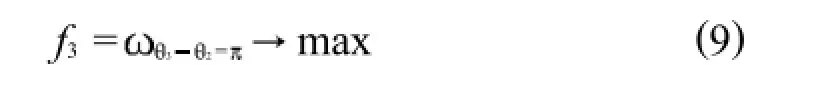
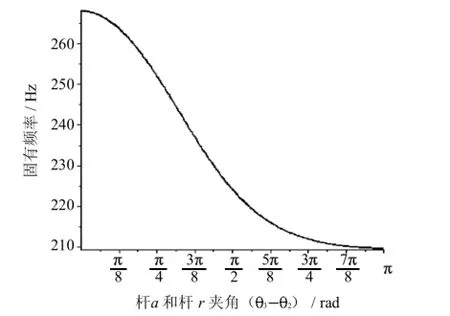
图6 机器人固有频率Fig.6 The natural frequency of the robot

1.3.4 误差影响系数

机器人机构中的制造误差、运动副间隙、磨损、摩擦等因素都会引起机器人位姿误差，通过几何误差建模，得到各个误差对终端输出误差的影响系数，为使终端输出误差较小，应该使误差影响系数尽量减小．对于机器人系统，它的末端输出运动误差E为

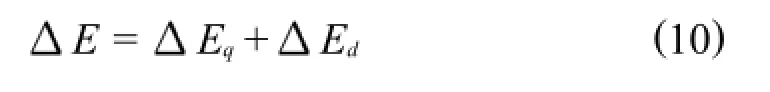
这里暂不考虑输入运动误差，只考虑结构尺寸带来的误差和动平台的精度问题．动平台的几何误差将会影响平台的柱坐标矢量rzT，经过分析可知，影响较大的因素为杆1涉及的几何误差对坐标分量r的影响、杆2涉及的几何误差对坐标分量r的影响以及杆3涉及的几何误差对坐标分量r和的影响，它们的影响系数分别为A1、A2、A31、A32，其表达式都是与杆长a，b和关节转角有关的函数．

这些几何误差对终端误差的影响系数绝对值之和为

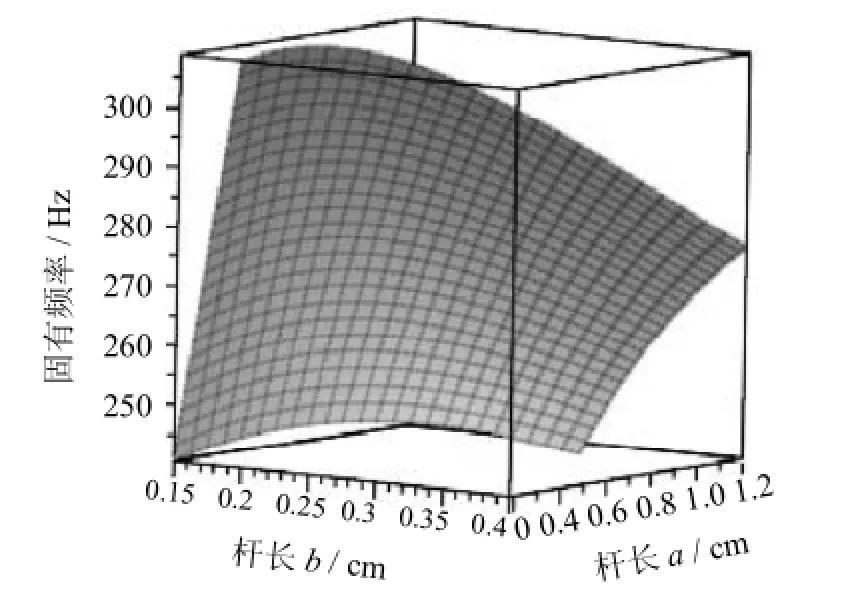
图7 固有频率随杆长变化图Fig.7 The natural frequency changes with rod length

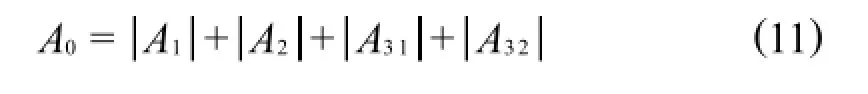
误差影响系数A0随杆长的变化情况如图8所示．将影响系数绝对值之和作为机器人性能优化的第4个优化目标函数：

1.4 约束条件

通过考虑机器人的设计要求，综合运动学以及动力学性能，机器人的杆长不应过小或者过大，给定机器人的杆长范围

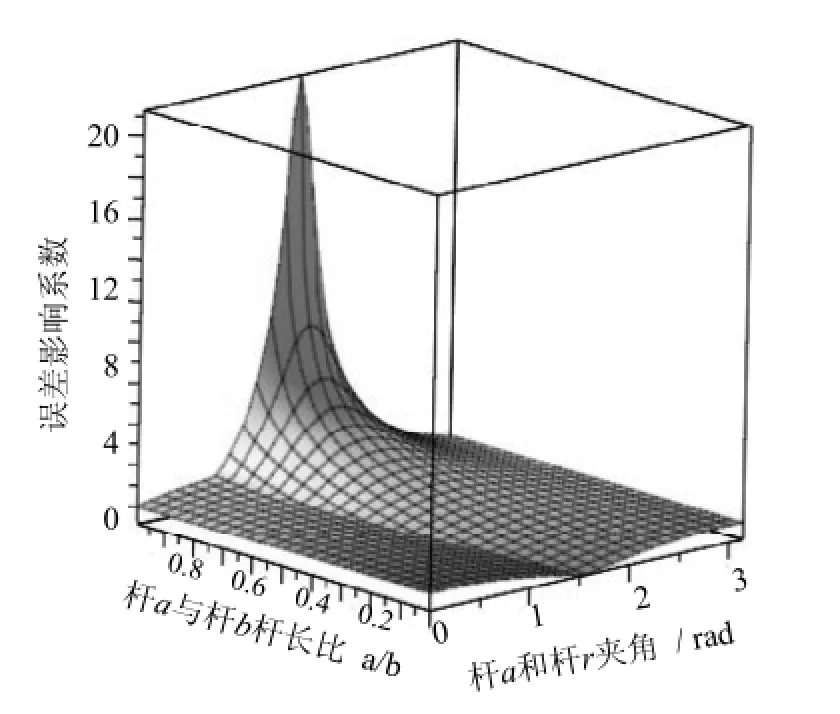
图8 误差影响系数随杆长变化图Fig.8 The natural frequency changes w ith rod length

此外，工作空间是一项非常重要的指标，而考虑到机构各构件的尺寸与工作空间的绝对大小关系很大，通常情况下增加杆长就会在一定程度上增大工作空间，但是单纯的增加杆长增大工作空间的同时，也会带来机构材料的消耗，为此，采用相对工作空间系数[13]大小作为另一约束条件．

相对工作空间系数定义为：K=V1/V．其中V表示包含机构和工作空间体积的圆柱体体积，V1表示工作空间体积大小．在类SCARA机器人机构中，增加曲柄和连杆的杆长，一般会降低相对工作空间系数，为了保证机构的性能，我们希望优化后的机构相对工作空间系数K不低于原有机构的50%．所以给定另一约束条件为

其中：Kini表示采用初始杆长时机构的相对工作空间系数．

通过给定杆长约束条件，可以保证机器人整体尺寸在一定范围内变化，不超出设计要求的许可．

1.5 问题描述

本文研究的目的就是找到最优的杆长，使类SCARA机器人的性能达到最优．通过对优化变量、优化目标以及约束条件的分析可以得到该优化问题的描述．

在保持机构构型不变的情况下，找到最优的杆长a和b，使优化目标f1和f3最大，同时让f2和f4最小，但不超出运动学及动力学要求的杆长限制．

可用数学表示如下

2 工程实例分析

2.1 优化方法

为解决类SCARA机器人的性能优化问题，我们采用的方法是将多目标遗传算法（Multi-Objective Genetic A lgorithm，MOGA）与BP神经网络（Back Propagation NeuralNetworks）算法相结合的方法．其具体流程如图9所示．

构建BP神经网络，用优化目标函数的输入输出数据训练BP神经网络，训练后的BP神经网络就可以预测函数输出．初始连接权值和阀值的选择对网络训练的结果影响较大，但有时无法准确获得，针对这些情况可以使用遗传算法优化BP神经网络的权值和阈值．种群中的每个个体都包含了1个网络所有权值和阈值，通过计算个体适应度值，找到最优的适应度值所对应个体，得到最优的权值和阀值，从而减小神经网络网络的预测误差．再将优化后的BP神经网络用于多目标遗传算法中预测个体适应度的值，使下一步多目标遗传算法计算效率更高．

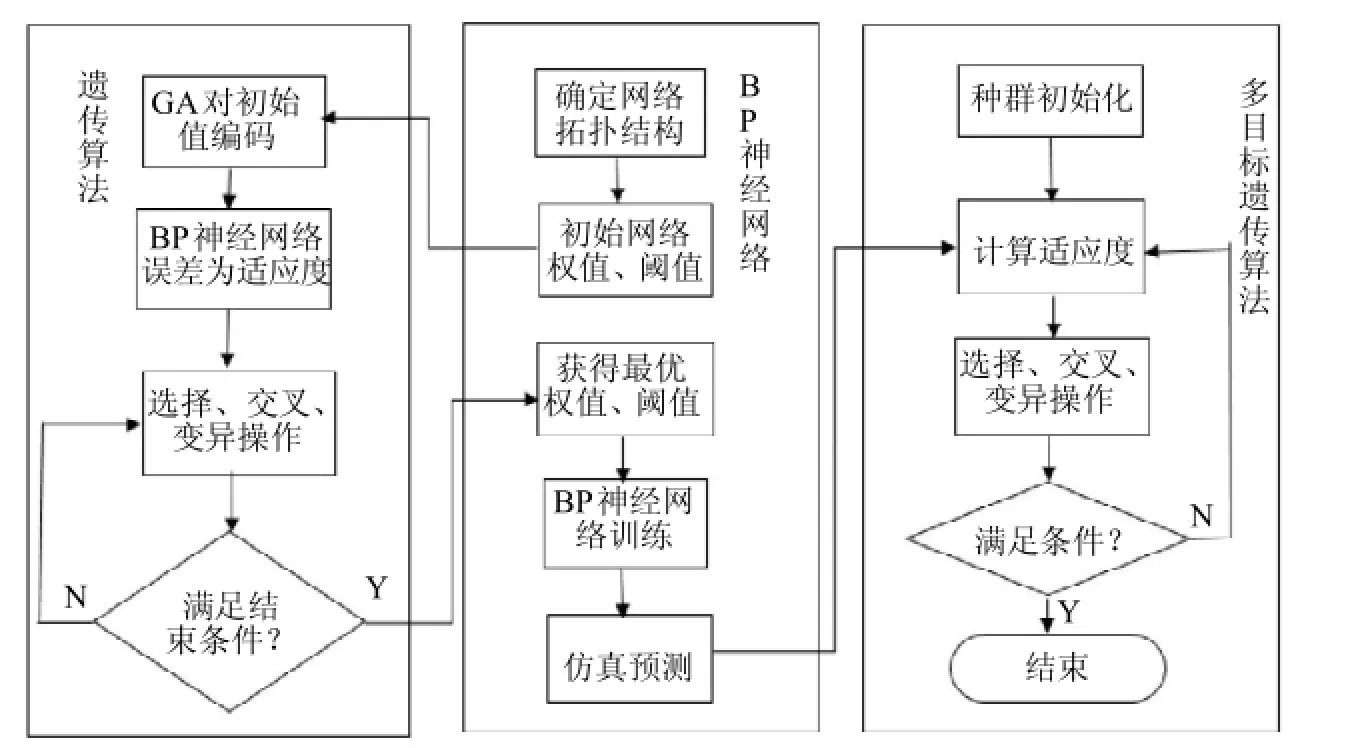
图9 优化方法原理图Fig.9 Optim ization schematics

2.2 优化结果及分析

根据机器人的工作空间及运动学等要求，设定机器人初始杆长为a=0.15 m，b=0.25 m．此时，机器人的4个优化目标函数值分别为：f1=0.180 4，f2=6.374，f3=257.94，f4=2.17．

然后根据设计变量、优化目标以及约束条件，编写MATLAB优化函数，设定遗传算法参数，ParetoFraction为0.3，PopulationSize为100，Generations为100，StallGenlim it为100，TolFun为1e-100．利用神经网络和遗传算法计算，运行程序，得到优化结果，从中选取10组pareto最优解，如表1所示．

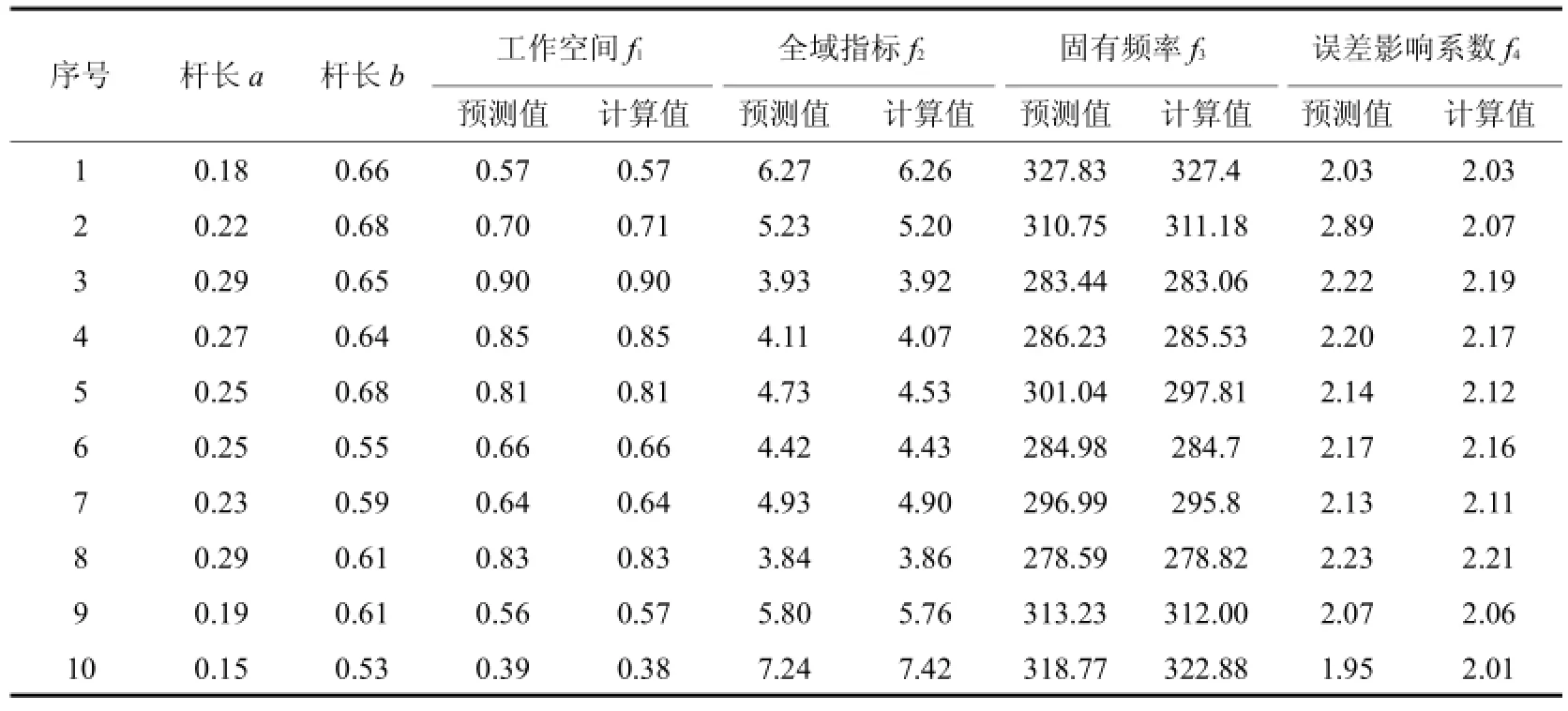
表1 优化结果Tab.1 Optim ization results

将优化所得结果与初始杆长进行比较，做出散点图，如图10所示．

经过比较可以发现，优化计算得到的这10组解可以使工作空间提高211%～394%，固有频率提高8%～27%，误差影响系数最多减小7.3%，全域条件数减小8%～37%．经过比较分析，最终选择a=0.22，b=0.68，这样机器人工作空间提高290.44%，固有频率提高20.6%，误差影响系数减小4.8%，全域条件数减小18.57%．运算时间约1 200 s，运算效率有很大提高．

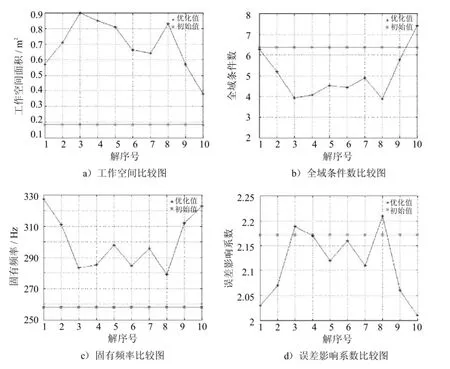
图10 优化结果对比图Fig.10 Contrast of optimization results

3 结论

通过对类SCARA并联机器人进行运动学和动力学的分析，得到了类SCARA机器人的多目标性能优化模型．将类SCARA机器人的工作空间、全域条件数、固有频率和误差影响系数作为优化目标，以杆长参数为优化变量，并以杆长和相对工作空间系数作为约束条件，进行了多目标优化．利用BP神经网络算法和多目标遗传算法相结合，既保证了算法的优化效果和也提高了算法的执行效率，最终经优化计算得到了可行的杆长参数，使机器人性能有了较大提高．

[1]邹慧君，高峰．现代机构学进展[M]．高等教育出版社，2007．

[2]Kumar A V．Waldron K J．The w orkspace of a mechanical m anipulators[J]．ASME Journal of M echanical Design，1981，103（3）：665-672．

[3]Salisbury JK，Craig J．A rticulated hands forcecontrol and kinematics issues[J]．The International JournalofRoboticsResearch，1982，l（l）：4-17．

[4]Angeles J．Kinematicsisotropyand theconditioning index of serial robotic manipulators[J]．The International JournalofRoboticsResearch，1992，11（6）：560-571．

[5]Gosselin C，Angeles J．A global performance index for the kinematic optimization of robotic manipulators[J]．Transactions of the ASME，1991，113（3）：220-226．

[6]刘爽，郭希娟，刘彬．基于Hessian矩阵的3-RR（RR）R并联机构的性能分析[J]．机械设计与研究，2006，22（5）：37-40．

[7]陈静，刘强．基于遗传算法的新型2-DOF并联机构优化设计[J]．机械设计，2008，25（2）：21-2．

[8]李瑞霞．五自由度并联机器人机构运动性能优化研究[J]．机床与液压，2015，3（3）：47-51．

[9]Zhang Lufan，Long Zhili，et al．Multi-objective optimization design of a connection frame in macro-m icro motion platform[J]．Applied Soft Computing，2015，32：369-382．

[10]Zhang Dan，Gao Zhen．Forward kinematics performance analysis and multi-objective optimization of a bio-inspired parallel manipulator[J]．Robotics and Computer-Integrated Manufacturing，2012，28（4）：484-492．

[11]Luo Jiman，Wang Dalon，etal．Multi-objectiveoptimalkinematic designof3-TPS/TPparallel robotm anipulator[J]．Advanced Engineering Forum Vols．2012，12（2）：324-329．

[12]张建军，王晓慧，徐闯，等．支链嵌套结构类SCARA并联机器人的时间最优轨迹规划[C]//第三十一届中国控制会议论文集B卷．合肥：中国自动化学会控制理论专业委员会，中国系统工程学会，2012：2503-2507．

[13]石志新，罗玉峰，陈红亮，等．一类新型并联机器人的尺度优化综合[J]．机器人技术，2005，32（1）：36-38．

[责任编辑 田丰夏红梅]

Multi-objective performance optimization of sim ilar-SCARA robot

ZHANG Jianjun，SHEN Aim in，KE Hui，YANG Gaowei

(School of M echanical Engineering,Hebei University of Technology,Tianjin 300130,China)

Based on the kinematics and dynam ics of the sim ilar-SCARA wafers handling robot,the performances,including the workspace,the global conditioning index,the natural frequency and the error effect coefficient are analyzed and optimized by multi-objective optim ization algorithm.The rod length parameters of the robot are design as the variable, and the w orkspace and other threeindexesare takenasthe fitness function.Given the rod length and the relativew orkspace coefficient constraints,a multi-objective genetic algorithm based on BP neural netw ork is used to solve this problem.The structure of the BP neural netw ork is optim ized by genetic algorithm to improve the prediction accuracy and reduce the computation time.Finally,a group of optimal rod length is calculated.The optim ized rod length parameters of the robot can improve the performance index of the robot greatly.

performance optim ization;neural network;genetic algorithm;multi-objective optimization

TP24

A

1007-2373(2015)06-0026-07

10.14081/j.cnki.hgdxb.2015.06.006

2015-05-22

国家自然科学基金（51175144）

张建军（1971-），男（汉族），教授，博士．

数字出版日期：2015-12-04数字出版网址：http://www.cnki.net/kcms/detail/13.1208.T.20151204.1536.008.htm l