基于OMP算法的振动信号去噪*

李建卓

(宝鸡文理学院 计算机科学系，陕西 宝鸡 721016)

基于OMP算法的振动信号去噪*

李建卓

(宝鸡文理学院 计算机科学系，陕西 宝鸡 721016)

针对机械振动信号在采集过程中容易夹杂大量噪声的问题，提出了一种使用正交匹配追踪算法用于实现振动信号与噪声的分离，从而达到了去除采集的振动信号中包含噪声的目的，并且还通过信噪比和均方误差这2个指标对去噪效果进行了检测。仿真结果表明，与使用传统的匹配追踪算法进行信号去噪的方法相比，正交匹配追踪算法不仅可以有效地滤除振动信号中夹杂的噪声，提高信噪比，还可以降低均方误差值，更好地防止振动信号的波形失真。

正交匹配追踪；振动信号；去噪

振动信号检测是对旋转机械进行状态监测和故障诊断的有效工具，但在实际工程采集时，振动信号很容易受到各种噪声的污染，有时甚至完全失真，从而对机械状态监测与故障诊断的正确性产生严重的干扰；因此，对振动信号进行去噪已经成为机械设备故障诊断研究的重要内容[1-4]。

匹配追踪(Matching Pursuit，MP)算法[5]是一种基于稀疏分解理论的信号处理方法，并且在地震监测、图像处理、医学信号检测和故障分析等领域[6-9]都得到了广泛的应用。MP算法的实质是先将信号在已构建好的过完备库中稀疏分解成多个原子，然后从中选出与信号最为相似的原子重构原始信号。目前，MP算法已被成功应用到多种信号的去噪中[10-13]。文献[14]已提出利用MP算法来去除振动信号中夹杂的噪声，虽然取得了显著的成效，但是由于MP算法每次迭代选择的原子可能并不是最优的，而是次最优的，故收敛时需要增大迭代次数；因此，本文提出采用正交匹配追踪(Orthogonal Matching Pursuit，OMP)[15-16]算法实现振动信号的去噪。OMP算法在MP算法的基础上，对选出的原子进行正交化处理，保证了每次迭代的最优性，不会重复选择原子，减少了迭代的次数[17]。仿真结果表明，OMP算法在对振动信号去噪时优于MP算法。

1 匹配追踪算法

匹配追踪算法的主要思想是根据最大匹配投影原理求解信号在过完备库中各个原子上的投影，然后对信号进行连续逼近。过完备库一般选为由调制后的高斯窗函数Gabor原子构成，其表达式为：

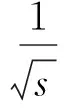
(1)

式中，s、u、v和w是信号的时频参数，分别代表尺度参数、位移参数、频率参数和相位参数。

将时频参数离散化后就可在过完备库中对信号进行稀疏分解，其分解过程如下。

1)选出与待分解信号f最为匹配的原子(即最佳原子) ψr 0，其满足以下条件：

(2)

2)将信号分解为在ψr 0上的分量和残余两部分，即为：

f=ψr0+R1f

(3)

式中，R1f为匹配后的残余信号。

3)对残余信号按式3形式重复i次迭代分解，即为：

Rif=ψri+Ri+1f

(4)

式中，是每次迭代后的最佳原子与上一次残余信号的内积，且ψr i满足：

(5)

4)由式3和式4可知，经过k次分解后，信号被分解为：

(6)

在信号长度有限时，随着k值的逐渐增大，信号残余的能量将以指数形式递减，最后收敛到0。

5)由上述可知原始信号f最终可分解为：

(7)

式中，k<

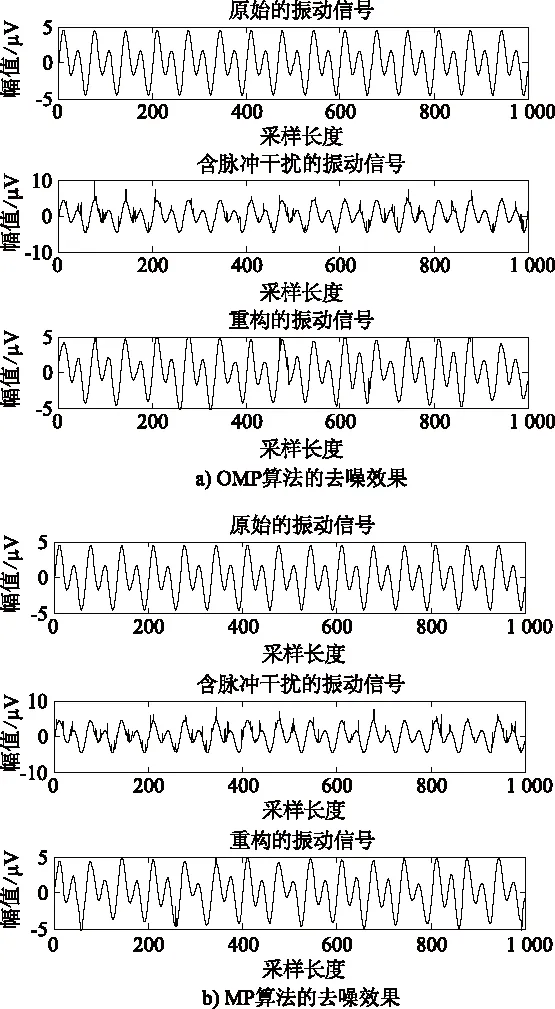
2 基于正交匹配追踪的去噪算法

2.1 正交匹配追踪算法原理

正交匹配追踪算法保留了匹配追踪算法的原子选择方式，都是根据最大匹配投影原理在过完备库中选取原子。假设已知过完备库D，初始信号为x，分解次数为k，进行OMP算法的信号分解的主要步骤如下。

1)选取原子。从D中选出与信号x最为匹配的原子Φrk，Φrk应满足最大匹配投影条件，即：

(8)

式中，Rkx为信号第k次分解后的残余信号。

2)正交化选取的原子。用Gram-Schmidt正交化方法对步骤1选择的原子Φrk进行正交化处理，即：

(9)

再对Uk进行归一化处理：

(10)

3)分解信号。可将信号分解成在Uk上的分量和残余两部分，即为：

(11)

2.2 去噪原理

假设含有噪声的振动信号为：

F=F′+N

(12)

式中，F′为要提取的原始振动信号，N为噪声。

根据原始的振动信号的波形特性选取对应的高斯函数构造过完备库D，然后将F在此过完备库中按照按照上述的OMP算法的步骤进行稀疏分解。随着迭代次数的增加，原始的振动信号成分不断被提取出来，当分解到一定阶段时，信号的有效成分可近似认为已被全部提取，从而实现振动信号与噪声的分离。

3 仿真实验及其结果分析

设用于仿真的振动信号f(t)的采样频率为2 000 Hz，其表达式为：

f(t)=3sin(2π60t)+2sin(2π30t)

(13)

在此振动信号中分别加入高斯白噪声和脉冲噪声，形成含有噪声的振动信号。

为了对去噪效果进行比较，分别使用OMP算法和MP算法对包含噪声的振动信号进行分解再重构，从而达到滤波噪声的目的。具体结果分别如图1和图2所示。迭代次数均设置为50次。

图1 高斯白噪声去噪前、后的波形图

图2 脉冲干扰信号去噪前、后的波形图

通过对图1、图2中原始的振动信号、包含噪声干扰的振动信号以及去噪后重构的振动信号的波形图进行比较，发现这两种算法都能够很好地剔除噪声，并且也都有效地保留了振动信号的波形特性，因此，在去噪后的波形图上并不能明显看出OMP算法与MP算法的差异；故采用信噪比SNR和均方误差MSE这两个指标对去噪效果进行评价，表达式分别如下：

(14)

(15)

式中，N为信号长度，f1(t)为输入信号，f2(t)为输出信号。

信噪比SNR和均方误差MSE可以客观、清楚地反映出对信号进行去噪的效果。信噪比的值体现了滤除噪声的能力，与算法的去噪性能成正比；均方误差的值体现了防止波形失真的能力，与算法的去噪性能成反比。依据式14和式15，分别计算出包含噪声干扰的振动信号与去噪后重构的振动信号的信噪比，以及去噪后重构的振动信号与原始的振动信号的均方误差，计算结果见表1和表2。表中，将包含噪声干扰的振动信号的信噪比记为SNR1，将去噪后重构的振动信号的信噪比记为SNR2。

表1 去除高斯噪声的效果表

表2 去除脉冲干扰的效果表

从表1可以看出，去噪后振动信号的信噪比(即SNR2)均得到了显著提高，均方误差也都接近于0，说明这两种算法都能够很好地消除噪声干扰，同时也能有效地防止波形失真。表中的数据还反映出相较于MP算法，使用OMP算法进行去噪后，信号的信噪比更大，均方误差值更小，说明在相同的迭代次数下，对振动信号进行去噪时，OMP算法的性能明显优于MP算法。

4 结语

本文采用OMP算法对包含噪声的振动信号进行去噪，并将其去噪结果与MP算法的去噪结果进行比较。仿真结果表明，OMP算法不仅可以很好地抑制噪声，还能够有效地保持振动信号的波形特征，并且其去噪后信号的信噪比较大，而均方误差较小，因此，其去噪性能优于传统的MP算法。

[1] 张文斌,杨辰龙,周晓军.形态滤波方法在振动信号降噪中的应用[J]. 浙江大学学报,2009,43(11):2096-2099.

[2] 陈彦龙,张培林,王怀光.基于量子叠加态参数估计的机械振动信号降噪方法[J]. 振动与冲击,2014,33(10):143-147,151.

[3] 熊炘,杨世锡,周晓峰.旋转机械振动信号的固有模式函数降噪方法[J]. 浙江大学学报，2011,45(8):1376-1381.

[4] 陈仁祥,汤宝平,马婧华.基于EEMD的振动信号自适应降噪方法[J].振动与冲击,2012,31(15):82-86.

[5] Mallat S G, Zhang Z. Matching pursuit with time-frequency dictionaries[J]. IEEE Transaction on Signal Processing, 1993, 41(12):3397-3415.

[6] 张繁昌,李传辉.地震信号复数域高效匹配追踪分解[J]. 石油地球物理勘探, 2013, 48(2): 171-175.

[7] 刘洋,郭树旭,张凤春,等.基于稀疏分解的指静脉图像去噪[J]. 信号处理,2012,28(2):179-185.

[8] 王利.数学形态学滤波在去除脑电伪迹中的应用[J]. 新技术新工艺,2014 (5):42-44.

[9] 孟庆丰,范虹,王祺,等.匹配追踪信号分解与往复机械故障特征提取技术研究[J]. 西安交通大学学报,2001,35(7):696-699.

[10] 司元雷.匹配追踪算法的超声多普勒血流信号降噪研究[J]. 无线通信技术,2012(3):57-61.

[11] 王利. 基于MP算法的脑电信号去噪[J]. 计算机与现代化,2014(4):102-104.

[12] 高显忠,侯中喜.基于改进MP稀疏分级的语音识别方法[J]. 计算机应用, 2009, 29 (6):1572-1574.

[13] 乔爱玲,马宏伟,刘涛.基于改进人工鱼群优化算法的超声信号稀疏分解[J]. 仪器仪表学报,2009,30(12):2480-2484.

[14] 李建卓.匹配追踪算法在振动信号去噪中的应用[J]. 计算机与数字工程, 2013 (12):1918-1919,1988.

[15] Tropp J, Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Transactions on Information Theory,2007,53(12):4655-4666．

[16] 马宁,王建新,董宁斐. 基于正交匹配追踪的欠采样LFM信号参数估计[J]. 电子与信息学报,2013,35(8):1888-1893.

[17] 杨真真,杨震,孙林慧.信号压缩重构的正交匹配追踪类算法综述[J]. 信号处理, 2013,29(4):486-496.

[18] 李慧,蔺启忠,王钦军,等.基于小波包变换和数学形态学结合的光谱去噪方法研究[J]. 光谱学与光谱分析,2010,30(3):644-648.

*陕西省科技厅自然科学基础研究计划项目(2014JQ2-6036)宝鸡文理学院硕士启动项目(ZK12112)

责任编辑彭光宇

VibrationSignalsDe-noisingbasedonOMPAlgorithm

LI Jianzhuo

(Department of Computer Science，Baoji University of Arts and Sciences，Baoji 721016，China)

Vibration signal is easily mixed up with a lot of noise during signal acquisition process. Use the orthogonal matching pursuit algorithm to separate vibration signal and noise, thereby removing noise, and the de-noising effect is tested by signal to noise ratio and mean square error. The experimental results show that comparing with matching pursuit algorithm, the orthogonal matching pursuit algorithm not only can effectively filtering noise and increase the SNR, but also be able to reduce the MSE and prevent waveform distortion better.

orthogonal matching pursuit (OMP)，vibration signal，de-noising

TP 391

:A

李建卓(1982-)，男，讲师，硕士，主要从事智能信息处理等方面的研究。

2015-03-06