星载三极子天线电磁波参数最佳估计算法

孙 杰张晓娟方广有刘延波

①(中国科学院电磁辐射与探测技术重点实验室 北京 100190)

②(中国科学院大学 北京 100190)

③(中国科学院光电研究院 北京 100094)

星载三极子天线电磁波参数最佳估计算法

孙 杰①②张晓娟*①方广有①刘延波②③

①(中国科学院电磁辐射与探测技术重点实验室 北京 100190)

②(中国科学院大学 北京 100190)

③(中国科学院光电研究院 北京 100094)

星载探测对仪器重量和体积的要求都很苛刻，而通常三极子天线需要一部三通道接收机以实现电磁波参数估计，不但重量和体积较大，而且存在通道串扰和增益不平衡的问题。该文提出两种基于时分技术的三极子天线估计电磁波参数的算法，使得一个三极子天线只需要一部单通道接收机，不但减小接收机的体积、降低接收机的重量和费用，而且克服了通道串扰和增益不平衡的问题。仿真结果证明了算法的有效性。

阵列信号处理；星载探测；电磁波参数估计

1 引言

随着阵列信号处理技术的发展，人们对电磁矢量天线给予了更多的关注。文献[1-4]研究了多个矢量天线组成大型的天线阵列来估计波达角的算法。文献[5-8]研究了分离式矢量天线求电磁波参数的方法，在克服共位矢量天线各成分间互耦问题的同时扩展了天线阵列的孔径。由于一个共位的矢量天线就能够同时估计多个不相关电磁波的参数，单矢量天线越来越引起人们的注意，尤其在空间探测等对天线占用空间有限制的应用场合。文献[9-11]重点研究了用完整(六成分)的电磁矢量天线进行参数估计的算法，而文献[12-19]则主要研究各种不完整电磁矢量天线(如三极子天线)如何估计电磁波频率和波达角的问题，文献[20]系统地论述了矢量天线进行信号处理的关键理论、方法及性能。

空间对地观测较地面观测具有观测范围广，不受地面自然条件限制的优势。采用星载探测仪对电离层和磁层电场进行探测，在日地空间物理研究，空间天气通过磁层和电离层与人类活动的互相影响研究等方面都具有重要意义[21]。卫星观测地震和火山活动引起的电磁场前兆异常信号不受地域的限制，越来越得到各国政府和科学家的重视。国际上目前已发射了以观测地震和火山喷发过程相关的电磁场变化为目的的多颗地震卫星[22]。由于飞行器的大小和容量是有限的，在保证探测仪器安全、可靠的前提下降低仪器的体积、重量始终是星载探测仪所追求的目标[23]。本文算法的提出就是为了在保证电磁波参数估计精度的同时，努力减小探测仪器的体积和重量，并克服通道串扰和增益不平衡引起的估计误差。

本文提出了两种基于时分技术的算法以实现一个三极子天线和一部单通道接收机同时估计多个电磁波参数。由于减少了两个接收通道，探测仪的体积，重量乃至费用都会降低，同时消除了通道串扰和增益不平衡引起的估计误差。本文提出的两种时分算法分别称为TD1算法和TD2算法。在叙述完两种时分算法的原理后，通过仿真实验将这两种算法与没有应用时分技术的原始算法做了比较，讨论了这两种时分算法的差别和适用性，并证明了这两种算法的有效性。

2 单个三极子天线估计频率和波达角的原理

本文所用三极子天线为3个成分沿着直角坐标系轴向伸展的矢量天线。

2.1 单个矢量天线估计波达角的原理

自由空间中的电磁波是横波，电场矢量垂直于波矢量k。如式(1)所示构建的矢量V平行于波矢量k[10]。

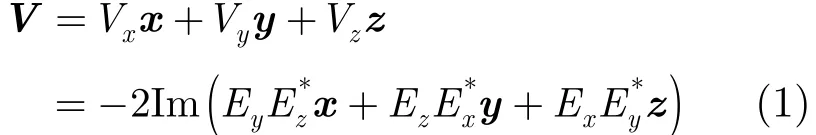
Ex, Ey, Ez表示复电场矢量在直角坐标系下3个坐标轴方向上的强度，上标∗表示复共轭，Im(⋅)表示取虚部运算。入射波的极角θ和方位角ϕ可根据Vx, Vy, Vz计算[17]：

对左手极化波：

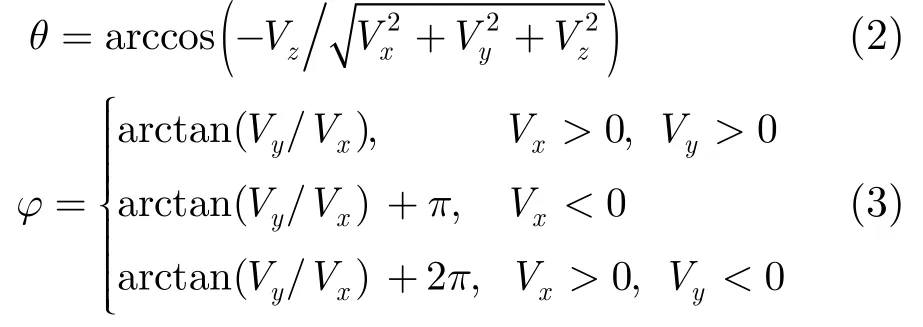
对右手极化波：

2.2 基于酉变换和矩阵束方法的频率估计算法

尽管一个天线阵子上接收到的信号就可以求出入射波的频率，但是如果入射波的波矢量与阵子的方向接近正交时，用该阵子上接收到的数据估计频率就会引入较大的误差，为了提高频率估计精度，需要3个阵子上的数据联合估计频率。有两种估计频率的算法[18]，一种是将3个通道的数据经过运算合成一路数据的算法，称为移相法；另一种是分别求3个通道的数据，再求平均的算法，称为平均值法。前者与后者相比，估计精度略有下降，但是运算速度快，所需时间仅为后者的1/3。

2.2.1 移相法估计频率 首先，根据式(6)计算出新数据DN×1(N为抽样点数)，其中，X,Y,Z表示3个通道的数据矢量。

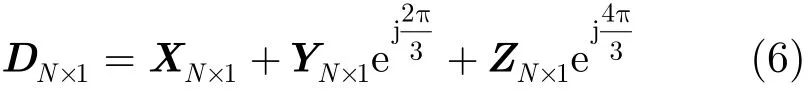
其次，为了提高运算速度，按照文献[19]的方法对合成的数据D进行酉变换得到实矩阵R。

最后，计算矩阵F的M个特征值γ1,γ2,…,γM：

此处，Re(⋅)表示取实部运算，Im(⋅)表示取虚部运算，且

第m个入射波的角频率ωm为

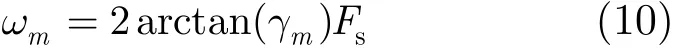
其中Fs为采样频率。2.2.2平均值法估计频率 平均值法先对单通道的数据进行频率估计，然后将3个通道估计的频率求平均。设x,y,z通道估计的频率值分别为ωxm, ωym,ωzm，则第m个入射波的角频率ωm为

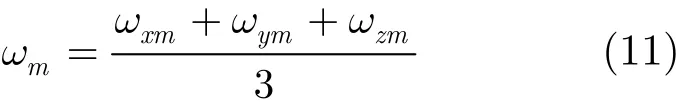
2.3 基于最小二乘算法的实时电场强度估计算法

根据估计出的角频率和采样时间间隔δ，构建矩阵H=(h1,h2,…,hm,…,hM)，此处hm=((ejωmδ)0,…, (ejωmδ)(N−1))T。第m个入射波在时刻的电场强度值构成了3个电场矢量，可获得3个超越方程为：

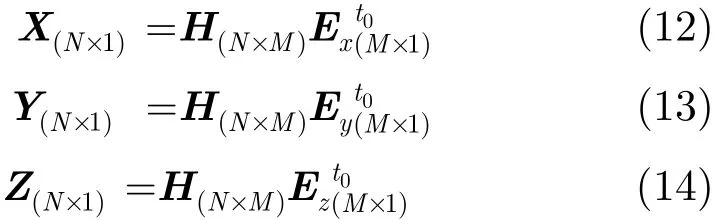
mm由式(1)～式(5)计算出。

2.4 电磁波极化参数估计算法

由于在上文中已经求出了电磁波的Ex, Ey, Ez3个电场分量和波达角(θ,ϕ)，根据矢量在直角坐标系到球坐标系的变换公式即式(15)，可以计算出Eθ和Eϕ：

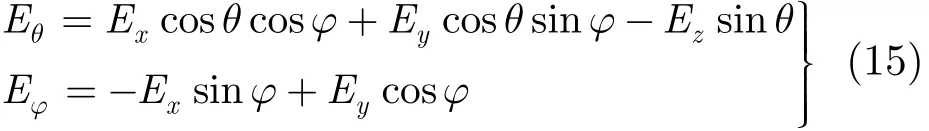
又因为

可求出：

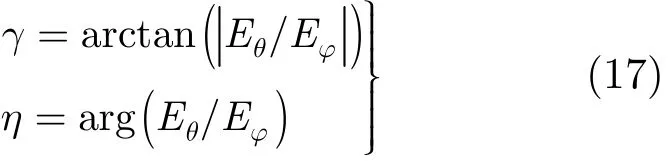
其中|⋅|表示取复数的模，arg(⋅)表示取辐角主值。

3 基于时分技术的波达角估计算法

根据电磁波理论，自由空间的同一个位置，不同时刻的电场强度满足Et0=Et0+Δte−jω×Δt。假设x方向的数据在t0时刻采样，y 方向的数据在t0+ Δt(Δt≥N⋅δ)采样，z 方向的数据在t0+2Δt时刻采样，则直角坐标系下的3个电场矢量表示为：。计算电场矢量强度的超越方程表示为

原始方法对三极子天线的3个成分同步采样，而TD方法通过分时采样来实现3个天线的数据共用一个接收机通道。

3.1 TD1算法

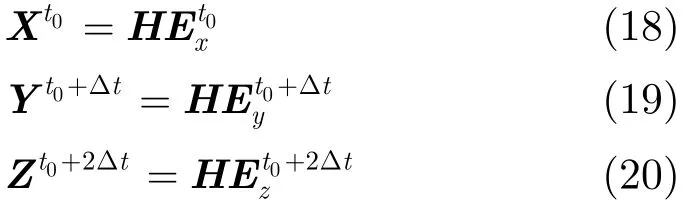
3.2 TD2 算法

三极子天线的3个阵子的数据交替抽样：x 方向的数据在t0,…,t0+(3N−3)⋅δ时刻采样，y 方向的数据在t0+δ,…,t0+(3N−2)⋅δ时刻采样，z 方向的数据在t0+2δ,…,t0+(3N−1)⋅δ时刻采样。用来计算瞬时电场强度Et0的矩阵H按如下方式构建：

此时获得式(21)～式(23)3个超越方程。

4 仿真实验

为了证明两种时分算法的有效性，本文将这两种算法与原始算法在相同的实验条件下做了对比。仿真实验中，入射波数量为5，噪声为零均值的加性高斯白噪声，信噪比从5 dB 到 30 dB范围变化，步进为5 dB，采样点数N=513。仿真结果为100次蒙特卡洛仿真的平均数据，采用均方根误差(RMSE)作为波达角和频率估计性能的恒量指标。

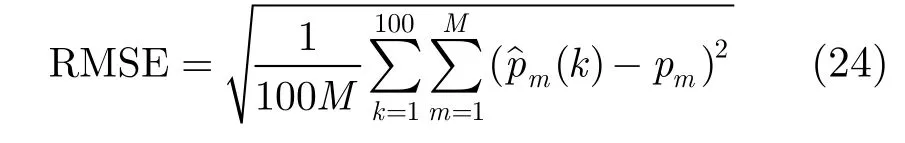
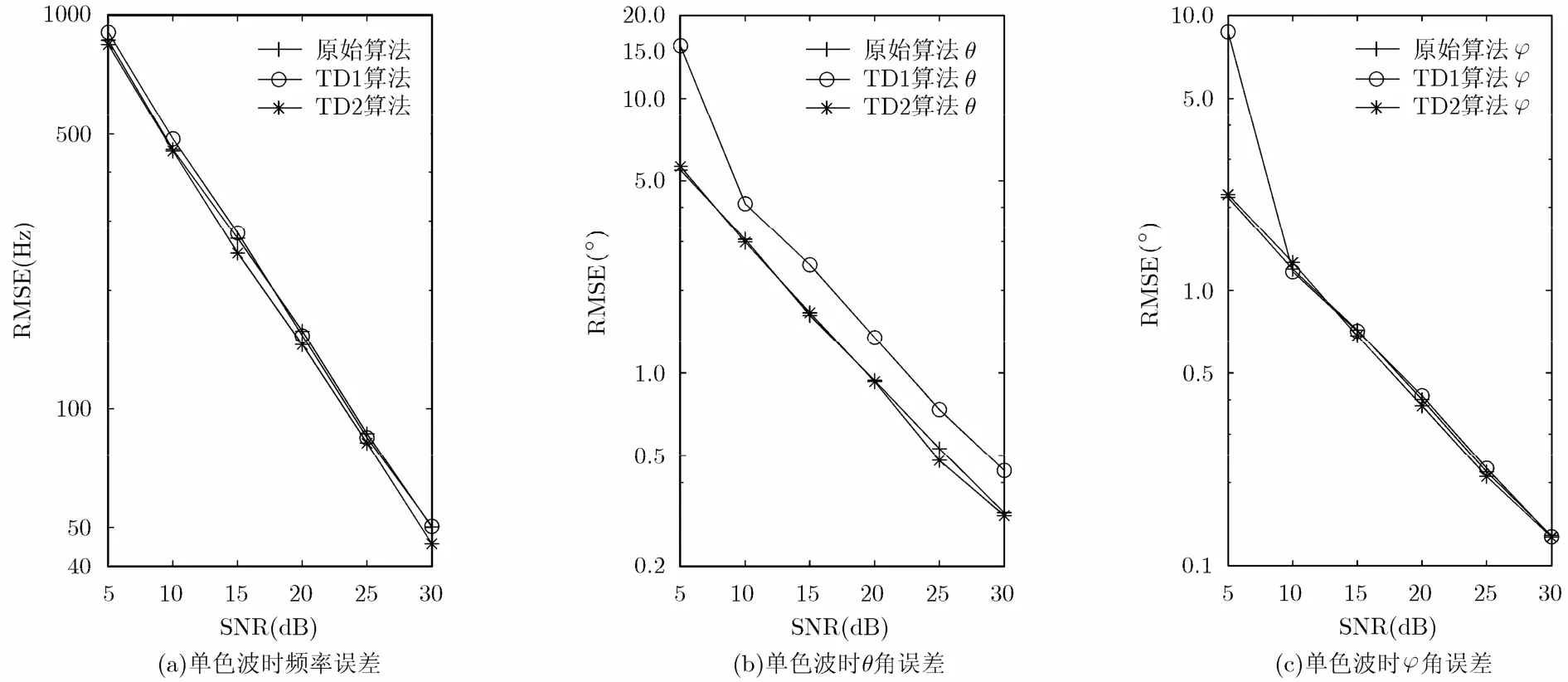
图1 电磁波为单色波时3种算法频率和角度估计的误差与信噪比的关系

实验1 当入射电磁波为单色波时，3种算法的频率和角度估计的误差与信噪比的关系如图1所示。从图1中可以看出，当入射电磁波为单色波时，3种算法频率估计误差相同；TD2算法与原始算法的极角θ估计误差相同，TD1算法略大；3种算法的方位角估计误差相同，只是在5 dB信噪比时，TD1算法估计误差比另外两种的估计误差大。

实验2 当入射电磁波为窄带时，3种算法的频率和角度估计的误差与信噪比的关系如图2所示。从图2可以看出，3种算法频率估计性能在低信噪比时相同，高信噪比时TD1算法最好，而原始算法最差，其原因在于：TD1算法的频率估计是平均值估计法，而另两种算法为移相估计法，且TD2算法因为交错采样引入了较长时间的累计，使得在高信噪比时估计误差略好于原始算法。3种算法的极角θ估计性能与单色波时一样，仍然是TD2算法与原始算法相同，TD1算法略大。但是方位角ϕ估计误差与单色波时已经不同，TD1角度估计误差比另外两种算法的误差稍有增大，尤其是在高信噪比时，而TD2算法与原始算法性能仍旧相同。

实验3 当入射电磁波为宽带时，3种算法的频率和角度估计的误差与信噪比的关系如图3所示。从图3可以看出，3种算法频率估计性能在低信噪比时基本相同，高信噪比时TD1算法最好，而原始算法最差，与窄带入射波时情况相同。角度估计的性能与窄带时情况相近，只是TD1算法的误差增大局势略降，因为此时频率估计精度略高的优势在宽带时比较明显。

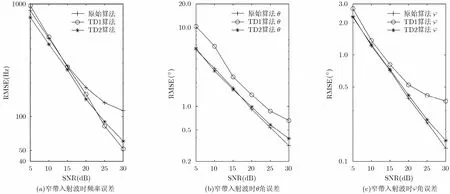
图2 电磁波为窄带波时3种算法频率和角度估计的误差与信噪比的关系

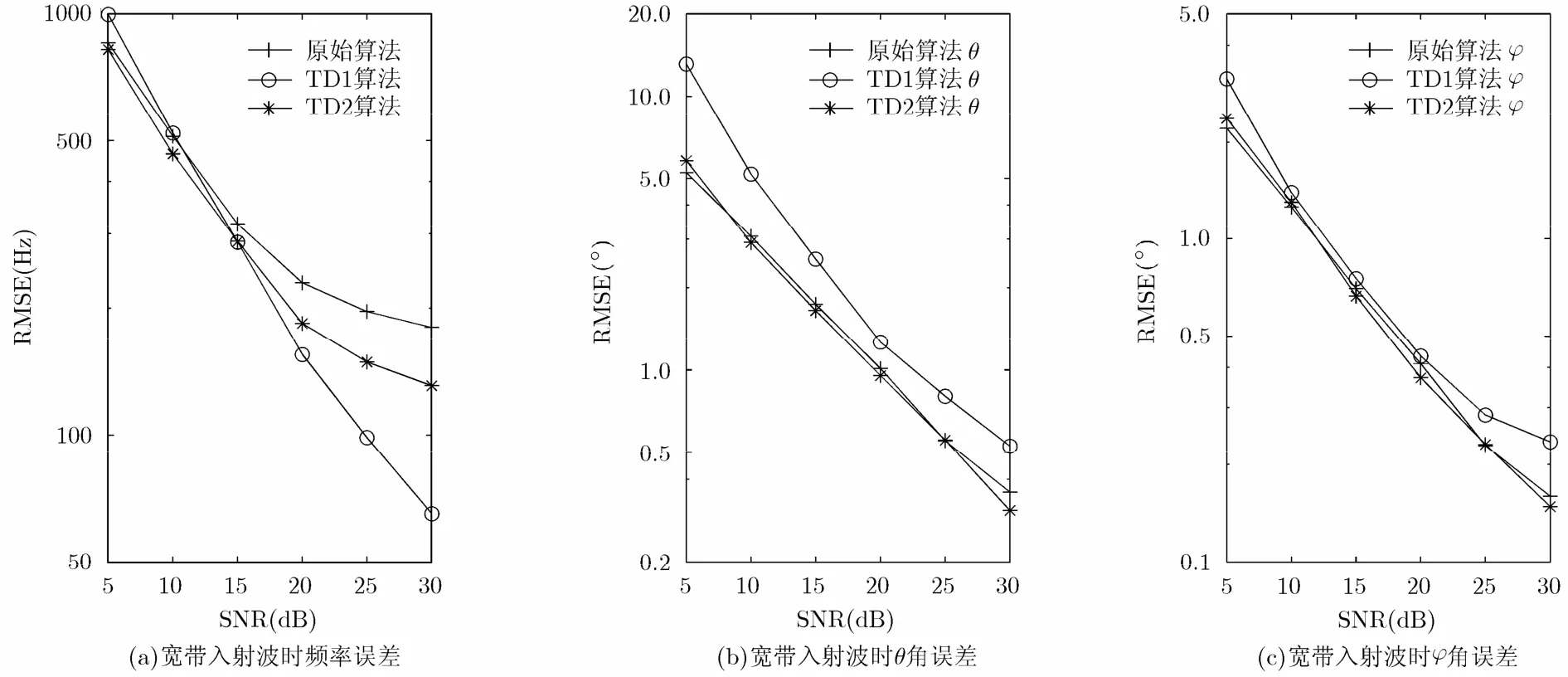
图3 电磁波为宽带波时3种算法频率和角度估计的误差与信噪比的关系

从3个实验可以得出如下结论：TD1算法因为3个通道在不同时刻采样，降低了通道间的相关性，导致角度估计误差有所增大；TD2算法因为交替采样，3个通道之间保持了很好的相关性，且由于延时带来的时间累计效应，频率估计性能略优于原始算法，而角度估计误差则与原始算法基本相同。由于TD2算法每隔δ时刻就要转换采样通道，故其更适合较低频率的探测需要，且通道切换控制部分与采样要严格同步，否则必然引入额外的估计误差，实现起来相对复杂。

5 结束语

本文提出的两种TD算法，无论入射波是何种带宽的信号，频率估计误差都与原始算法相当甚至在高信噪比时略优；而TD1算法的极角估计误差总是略差，方位角估计误差在单色波性能与原始算法相当，窄带和宽带时略差；TD2算法的角度估计性能保持与原始算法相当。因此，两种时分算法在保证参数估计性能不变的前提下，可以实现一个三极子天线和一部单通道接收机估计电磁波参数，从而克服三通道接收机的通道串扰、增益不平衡等问题，降低接收机的体积、重量和费用，更适合空间星载探测的需要。

[1] 周杰, 邱琳, 菊池久和. 基于电磁矢量传感器的 MIMO天线阵列系统研究[J]. 通信学报, 2013, 34(5): 1-11.

Zhou Jie, Qiu Lin, and Hisakazu Kikuchi. Analysis of MIMO antenna array based on electromagnetic vector sensor[J]. Journal on Communications, 2013, 34(5): 1-11.

[2] He J and Liu Z. Computationally efficient 2-D direction finding and polarization estimation with arbitrarily spaced electromagnetic vector sensors at unknown locations using the propagator method[J]. Digital Signal Process, 2009, 19(3): 491-503.

[3] Gao X, Zhang X, Sun Z, et al.. On multilinear-based approaches of blind receiver for polarization sensitive uniform square array [C]. Proceedings of International Conference on Wireless Networks and Information Systems, Shanghai, China, 2009: 338-342.

[4] Mir H S, Sahr J D, Keller C M, et al.. Source localization using airborne vector sensors[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Philadelphia, USA, 2005: 1033-1036.

[5] Xin Yuan. Coherent sources direction finding and polarization estimation with various compositions of spatially spread polarized antenna arrays[J]. Signal Processing, 2014, 102(9): 265-281.

[6] 樊劲宇, 顾红, 苏卫民, 等. 偶极子分离的矢量阵MIMO雷达多维角度估计算法[J]. 电子与信息学报, 2013, 35(8): 1841-1846.

Fan Jin-yu, Gu Hong, Su Wei-min, et al.. MIMO radar multidimension angle estimation with electromagnetic vector of noncollocating dipoles/loops[J]. Journal of Electronics & Information Technology, 2013, 35(8): 1841-1846.

[7] 郑桂妹, 陈伯孝, 杨明磊. 改进分离式电磁矢量阵列的两维波达方向估计[J]. 电波科学学报, 2014, 29(2): 213-220.

Zheng Gui-mei, Chen Bai-xiao, and Yang Ming-lei. Twodimensional DOA estimation with an improved spatially separated electromagnetic vector sensor array[J]. Chinese Journal of Radio Science, 2014, 29(2): 213-220.

[8] 郑桂妹, 陈伯孝, 吴渤. 三正交分离式极化敏感阵列的波达方向估计[J]. 电子与信息学报, 2014, 36(5): 1088-1093.

Zheng Gui-mei, Chen Bai-xiao, and Wu Bo. DOA estimation with three orthogonally oriented and spatially spread polarization sensitive array[J]. Journal of Electronics & Information Technology, 2014, 36(5): 1088-1093.

[9] Wong K T. Direction finding/polarization estimation-dipole and/or loop triad(s)[J]. IEEE Transactions on Aerospace andElectronic Systems, 2001, 37(2): 679-684.

[10] Bergman J. Present and future applications of the information dense antenna[OL]. http://www.physics.irfu.se/ Publications/Conferences/BergmanEtAl:HF04:2004.pdf, 2014. 5.

[11] Mir H S and Sahr J D. Passive direction finding using airborne vector sensors in the presence of manifold perturbations[J]. IEEE Transactions on Signal Processing, 2007, 55(1): 156-164.

[12] Appadwedula S and Keller C M. Direction-finding results for a vector sensor antenna on a small UAV [C]. 4th IEEE Sensor Array Multichannel Signal Processing Workshop, Waltham, USA, 2006: 74-78.

[13] Xu Y and Liu Z. Adaptive quasi-cross-product algorithm for unitripole tracking of moving source[C]. International Conference on Communication Technology, Guilin, China, 2006: 1-4.

[14] Daldorff L K S, Turaga D S, Verscheure O, et al.. Direction of arrival estimation using single tripole radio antenna[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, China, 2009: 2149-2152.

[15] Au-Yeung C K and Wong K T. CRB: sinusoid-sources' estimation using collocated dipoles/loops[J]. IEEE Transactions on Aerospace & Electronic Systems, 2009, 45(1): 94-109.

[16] Yuan X, Wong K T, Xu Z, et al.. Various triad compositions of collocated dipoles/loops, for direction finding & polarization estimation[J]. IEEE Sensors Journal, 2012, 12(6): 1763-1771.

[17] 孙杰, 张晓娟, 方广有. 近地面三阵子天线估计电磁波到达角和极化参数[J]. 物理学报, 2013, 62(19): 198402-1-198402-5.

Sun J, Zhang X J, and Fang G Y. Direction of arrival of EMW and polarization parameter estimation using tripole near the earth surface[J]. Acta Physica Sinica, 2013, 62 (19): 198402-1-198402-5.

[18] Chen L, Aminaei A, Falcke H, et al.. Optimized estimation of the direction of arrival with single tripole antenna[C]. Antennas & Propagation Conference, Loughborough, UK, 2010: 93-96.

[19] Yilmazer, Jinhwan Koh, and Sarkar T K. Utilization of a unitary transform for efficient computation in the matrix pencil method to find the direction of arrival[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(1): 175-181.

[20] 徐友根, 刘志文, 龚晓峰. 极化敏感阵列信号处理[M]. 北京:北京理工大学出版社, 2013: 1-9.

Xu You-gen, Liu Zhi-wen, and Gong Xiao-feng. Signal Processing Based on Polarization Sensitive Array[M]. Beijing: Beijing Institute of Technology Press, 2013: 1-9.

[21] 任仁, 陈贤详, 夏善红, 等. 空间电磁环境监测用双探针式星载电场探测仪[J]. 电子与信息学报, 2012, 34(10): 2489-2493.

Ren Ren, Chen Xian-xiang, Xia Shan-hong, et al.. Spaceborne double-probe electric field sensor for space electromagnetic environment monitoring[J]. Journal of Electronics & Information Technology, 2012, 34(10): 2489-2493.

[22] 汤吉, 赵国泽, 陈小斌, 等. 地震电磁卫星载荷及现状[J]. 地球物理学进展, 2007, 22(3): 679-686.

Tang Ji, Zhao Guo-ze, Chen Xiao-bin, et al.. Introduction of payload for electro-magnetic emissions on seismic satellite[J]. Progress in Geophysics, 2007, 22(3): 679-686.

[23] Hegg J. Enhanced space integrated GPS/INS(SIGI)[J]. IEEE Aerospace and Electronic Systems Magazine, 2002, 17(4): 26-33.

孙 杰： 女，1976年生，工程师，研究方向为电磁波参数估计和信号处理、辐射源定位.

张晓娟： 女，1964年生，研究员，博士生导师，主要研究方向为微波遥感、天线、计算电磁学、电磁散射与逆散射.

方广有： 男，1963年生，研究员，博士生导师，主要研究方向为超宽带电磁学理论及应用、超宽带成像雷达技术、微波成像新方法、新技术.

The Optimized Parameters Estimation of Electromagnetic Wave with Spaceborne Single Tripole Antenna

Sun Jie①②Zhang Xiao-juan①Fang Guang-you①Liu Yan-bo②③

①(Key Laboratory of Electromagnetic Radiation and Sensing Technology, Chinese Academy of Sciences, Beijing 100190, China)

②(University of Chinese Academy of Sciences, Beijing 100190, China)

③(Academy of Opto-Electronics, Chinese Academy of Sciences, Beijing 100094, China)

It is well-known that restricts on weight and volume of spaceborne sensing instruments are strict. Single tripole antenna usually needs one three-channel receiver to estimate the parameters of electromagnetic waves. When the weight of the receiver is high and the volume is big, channel garbling and gain imbalance exist. This paper puts forward two algorithms based on Time Division (TD) method with tripole antenna for parameter estimation of electromagnetic waves. The two methods make it possible that a single tripole antenna needs only a one-channel receiver, which not only decreases the volume and weight of the receiver, but also reduces the cost and overcome channel garbling and gain imbalance. The simulations prove the validity of the proposed algorithms.

Array signal processing; Spaceborne sensing; Parameters estimation of electromagnetic waves

TN911.7

： A

：1009-5896(2015)06-1378-06

10.11999/JEIT141241

2014-09-23收到，2015-01-19改回

国家自然科学基金(61172017)资助课题

*通信作者：张晓娟 xjzhang@mail.ie.ac.cn