一种MIMO雷达多模式波形优化设计方法

王 旭 刘宏伟 纠 博吴 梦 保 铮

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

一种MIMO雷达多模式波形优化设计方法

王 旭 刘宏伟 纠 博*吴 梦 保 铮

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

在多目标多任务情况下，通常要求雷达具有多种工作模式，以实现搜索、跟踪等不同功能。传统雷达在某一时刻只能实现一种功能，工作模式不够灵活，很难高效利用系统资源。针对此问题，该文提出一种MIMO雷达多模式波形设计方法，该方法以方向图逼近、期望方向的信号功率谱或频谱逼近等为准则，在恒模约束下建立关于波形矩阵的多目标优化模型，并采用共轭梯度方法进行优化求解。仿真结果表明，所设计波形在空域上具有多波束方向图，波束指向上的信号具有多种工作模式的特性，可以同时实现搜索、跟踪等功能。

MIMO雷达；波形设计；发射方向图；多波束；多功能

1 引言

多输入多输出(MIMO)雷达的特点是具有多个发射和接收天线[1−11]，并且各发射天线可以发射不同信号。根据天线的布置方式，MIMO雷达可分为分布式MIMO雷达[1]和集中式MIMO雷达[2]。集中式MIMO雷达的天线间距较小，与相控阵雷达相比，MIMO雷达具有波形分集的优势，可以获得更高的角度分辨率，更好的参数辨别能力、抗截获能力和杂波抑制能力[11]。此外，还可以针对不同场景不同需求，充分利用MIMO雷达发射端的自由度，灵活地进行发射波形设计[2−15]，以采用不同模式满足不同需求和功能，提升系统性能。

传统雷达一般具有定向的窄波束，因此对于大范围的角度覆盖内的目标搜索，要求窄波束快速往复地在空域内扫描，以保证期望空域覆盖范围内所有目标可以被有效地探测到；对于已探测到的目标，即可以根据目标的运动情况调整波束指向，以进行目标跟踪；或者向已发现的目标发射特定的信号(如宽带)，进行雷达成像、目标分类和识别。根据实际场景的复杂性和多变性，要求一部雷达同时具备多种功能。对于不同的功能，发射不同的信号。传统相控阵雷达的多功能是依靠时间分割来实现的，通常雷达在某一时刻只能实现一种功能[16](同一时刻只能发射一种波形)，工作模式不太灵活，无法有效利用系统资源。而MIMO雷达由于在发射端和接收端均采用数字阵技术，各个发射天线发射不同信号，可以使雷达在某一时刻同时完成多个功能，实现真正意义上的多功能雷达。

MIMO雷达波形设计主要涉及正交波形设计、发射方向图综合等方面。目前正交波形设计主要基于阵元间信号的正交性，正交波形具有全向的方向图[2]，抗截获能力强，可用于目标搜索。为了获得足够的目标检测性能，需要进行一定时间内的脉冲积累，但对于高速目标，可用于积累的时间有限，因此正交波形较适用于低速目标的检测。而发射方向图综合主要解决雷达系统空间能量的配置问题[3−13]，可用于多目标的跟踪等场合。主要包括基于发射方向图的波形相关矩阵设计与基于相关矩阵的恒模波形设计。对于前者，主要通过相关矩阵的设计实现期望的发射方向图[4−9]，目前大多采用方向图匹配模型，利用凸规划方法[5,6]及参量化相关矩阵法[7]进行求解，文献[8,9]在方向图匹配模型的基础上考虑了主瓣波动和旁瓣电平，可以在方向图逼近的同时降低主瓣波动和旁瓣电平；对于后者，主要通过对恒模波形的设计逼近最优的相关矩阵或期望发射方向图[10−15]，有效的方法有循环算法[10](Cyclic Algorithm, CA)、非线性映射[11]、基波束[12,13]，但此类方法大多只考虑了方向图特性，而未考虑时域合成信号的脉冲压缩特性。另外，文献[14]提出了一种基于发射端矩阵加权的方向图设计方法，但所设计波形无法满足恒模约束；文献[15]针对多波束的方向图逼近和波束指向方向上信号的自相关、互相关旁瓣抑制，提出了关于波形的无约束优化模型，并采用迭代拟牛顿法求解，由于基于最小化积分旁瓣准则，对峰值旁瓣抑制效果有限。

现有的MIMO雷达波形设计方法多未考虑适用于复杂场景下的多功能情况，即所设计的波形仅符合单一工作模式，如适用于慢速目标探测的正交波形或宽波束波形，适用于多目标跟踪的多波束。为了分析、研究MIMO雷达在多功能方面的优势，实现同时多功能，本文提出一种MIMO雷达多模波形优化设计方法。通过方向图逼近实现针对多目标的多波束，利用功率谱或频谱逼近使波束方向具有符合不同工作模式的波形，基于以上准则建立关于波形相位矩阵的多目标优化模型，利用共轭梯度方法优化发射波形。所设计波形在空域上具有多波束方向图，波束指向方向信号具有不同时域波形(频域特性)或带宽，不同方向信号具有多模(多种工作模式)特性，可以实现不同功能。

2 问题描述

假设一集中式MIMO雷达的发射阵列是由M个全向天线构成的均匀线阵(ULA)，如图1所示，阵元间距为d，第m个天线发射的信号可以表示为

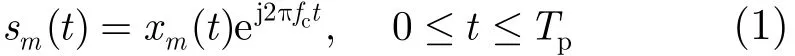
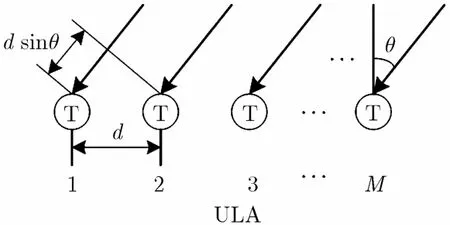
图1 MIMO雷达发射阵列

其中xm(t)表示第m个天线发射的基带信号，fc是信号载频，Tp是脉冲宽度。不失一般性，忽略传播衰减，发射信号在远场方向θ处合成的信号为

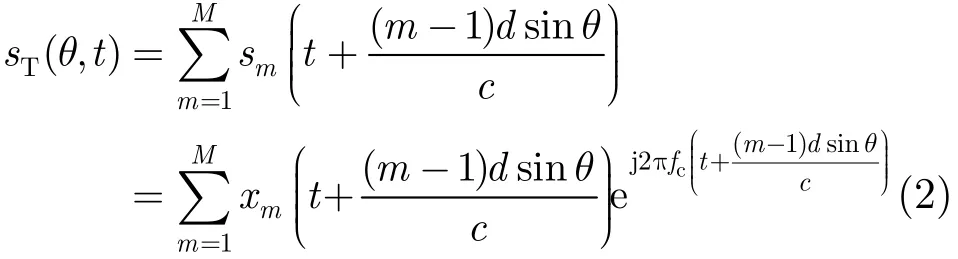
方向θ处合成信号在频域可表示为

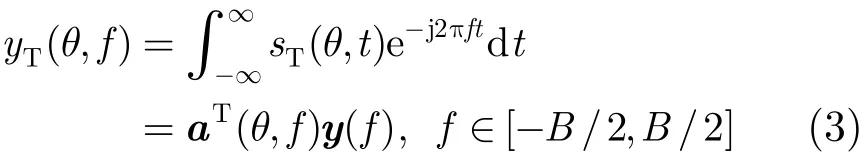
12M信号的频谱，ym(f)表示基带信号xm(t)的频谱，即

本文考虑离散基带发射信号，即xm(l)=,l=1,2,…,L ，其中Ts=1/B表示采样率，L=Tp/Ts表示码长。因此采样后的离散基带发射信号可以表示为X=[x1,x2,…,xL]，其中xl= [x(l),x(l),…,x(l)]T表示在(l−1)T至lT时间段内

12Mss

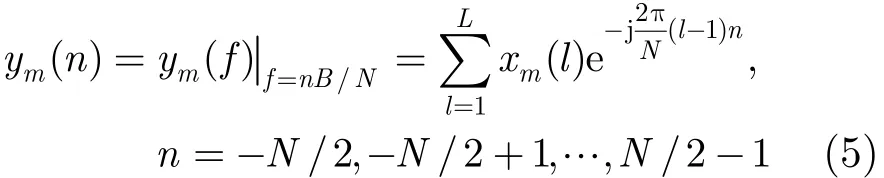
M个阵元发射的基带信号。根据离散傅里叶变换，基带信号的频谱可按式(5)采样其中N表示离散傅里叶变换的点数。因此，在频率f=nB/N 处M个基带信号的频谱为yn=[y1(n ), y2(n),…,yM(n)]T=Xfn，其中fn=[1,e−j2πn/N,…, e−j2πn(L−1)/N]T表示N点DFT中第n个频点处的变换向量。

从而，θ方向信号的N点频谱和功率谱可写为

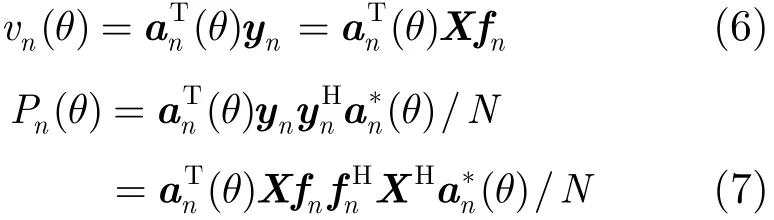
其中

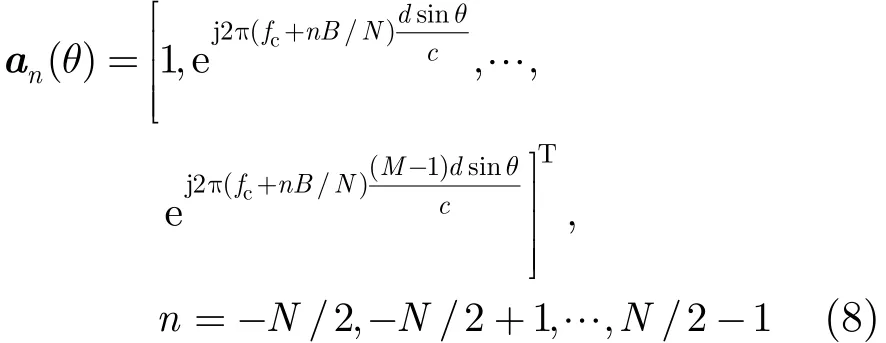
表示在频率nB/N+fc处的导向矢量。其中pn(θ)反映了发射信号在频率nB/N+fc处的空域功率分布，类似于时域某时刻方向图的定义。因此，定义离散基带信号的方向图为θ方向信号的离散功率谱之和，即

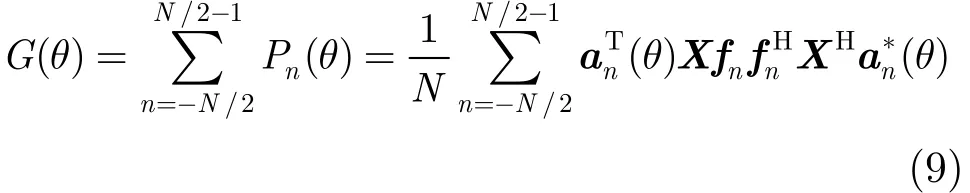
θ方向信号的频谱vn(θ)和功率谱Pn(θ)反映了θ方向信号的形式、带宽等，对在不同场景下的不同目标应具有不同特性；方向图G(θ)反映了雷达发射信号在空间的功率分布，决定了目标方向的功率，从而影响目标回波的SNR。

3 多模波形设计

在多目标场景下，需要根据不同目标，设计多种模式的波形以分别满足不同功能。目前，雷达脉冲压缩信号主要包括线性调频信号(Linear Frequency Modulation, LFM)，非线性调频信号(NLFM)和相位编码信号等。LFM具有斜刀刃状的模糊函数，压缩脉冲形状和SNR对多普勒频移不敏感；NLFM信号具有较低的时域旁瓣，对多普勒频移较敏感；相位编码信号具有自由度高、设计灵活、时域旁瓣低的特点，但对多普勒频移很敏感，需要在接收端使用能覆盖多普勒频移可能范围的匹配滤波器组。因此LFM信号比较适用于目标多普勒频率未知的目标搜索；而相位编码信号较适合多普勒频率已知的目标跟踪阶段。MIMO雷达正交波形亦可以用于目标搜索，但需要进行长时间积累以获得与窄波束相同的SNR，这限制其较适用于低速目标的检测。基于此，本文考虑采用具有LFM特性的信号进行目标搜索，相位编码信号用于目标跟踪。在实际中，通常采用三坐标雷达的针状波束进行目标跟踪，为了简化模型，本文仅考虑两坐标雷达的波形设计。

随着数字器件在雷达系统中的应用，LFM和NLFM信号均可以用一定采样率的离散信号表示，因此可用相位编码信号进行近似。为了最大化发射机的工作效率，发射波形需要具有恒模特性。因此，第m个天线发射的波形可以表示为xm(l)=ρejϕml，其中ϕml表示xm(l)的相位，不失一般性，本文取ρ=1。定义波形X的相位矩阵为

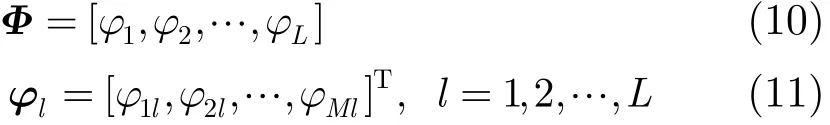
因此θ方向信号的功率谱和离散基带信号的方向图，即式(7)和式(9)可用相位矩阵Φ表示为

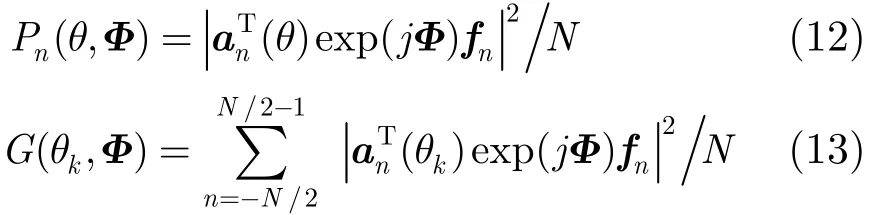
其中exp(jΦ)中各元素表示模值为1的复数，其相位为Φ中的相应元素。

为了实现针对不同目标发射具有不同功能的波形，需要在空域上形成指向目标方向的多个波束；不同波束指向上的信号需具有特定的频谱或功率谱，以实现不同功能。因此可以针对方向图逼近和功率谱逼近建立关于相位矩阵的如下优化模型：

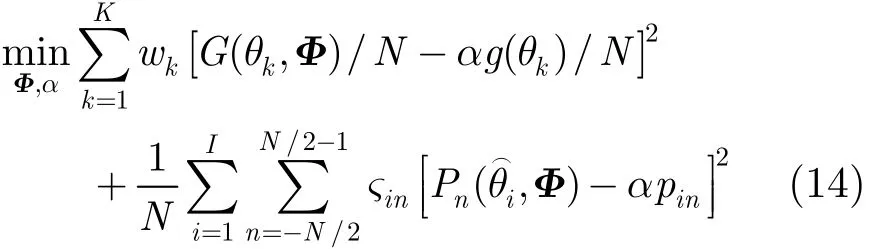
离散方位角，K表示离散化方位角总数，α≥0表示尺度因子，表示不同方位角处的方向图逼近权重，表示方向上不同频点处的功率谱逼近权重。第1项表示方向图逼近，第2项表示期望方向功率谱逼近。第1项中G(θk,Φ)/N 表示θk方向信号平均功率谱，因此第1项可以看成是各方向信号平均功率谱的逼近。为了保证所设计波形在波束指向方向上具有期望的功率谱特性(时域自相关特性)，本文取式(5)中的DFT点数为N=2L。

通过设定期望的方向图g(θk)，第1项可以保证所设计波形具有期望的功率分布，如多目标场景中的多波束；根据不同的功能需要，设定波束指向方向上信号的期望功率谱，可以保证所设计波形具有期望特性，如对于目标识别或成像，可以在所需带宽内设置白的期望功率谱。另外理想的自相关函数(旁瓣电平较低)具有特定的信号功率谱，因此可以通过设计信号的功率谱具有特定的分布(如加Hamming窗的LFM的功率谱)以保证信号的自相关函数具有较低的旁瓣电平。对于某个相位矩阵Φ，其对应的最优尺度因子α可表示为

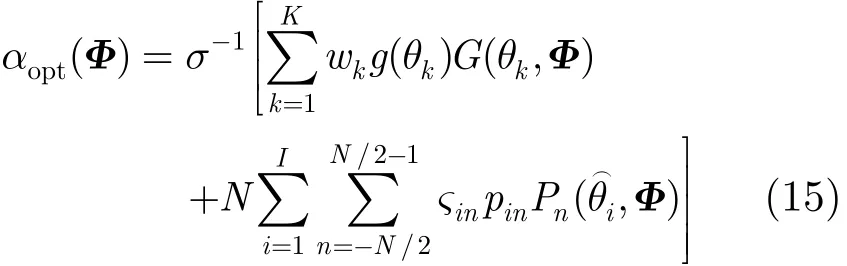
对于已检测或跟踪的目标，可以根据期望功率谱，设计用于跟踪或成像的波形，为了实现针对目标搜索的具有LFM特性的信号，采用功率谱逼近的方式，不能保证所设计波形在搜索方向上具有LFM信号的特性。因此对于需要具有搜索功能的雷达波形，采用式(16)的代价函数其中C1表示式(14)中的目标函数，ηi≥0表示权重，i=1,2,sLFM表示幅度为ρ的线性调频信号，β表示对应线性调频信号的尺度因子，F=表示L×L维的FFT矩阵，其中表示L点

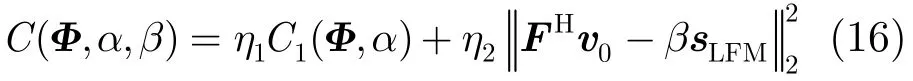
DFT中第l个频点对应的变换向量， v0=表示θ0方向信号频谱。式(16)中权重{ηi}可以根据实际需要、经验确定，本文采用多目标优化中的α-方法[17]确定。式(16)中的第2项可进一步表示为

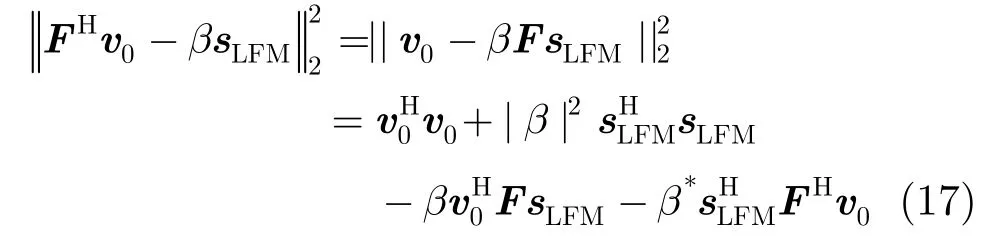
因此最优的尺度因子β可以表示为相位矩阵Φ的函数。

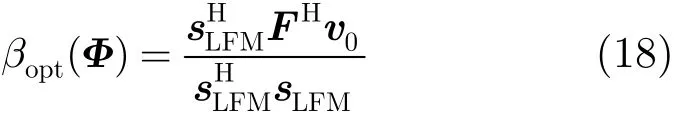
将式(15)与式(18)代入代价函数式(16)后，可得到如下关于相位矩阵的优化模型：

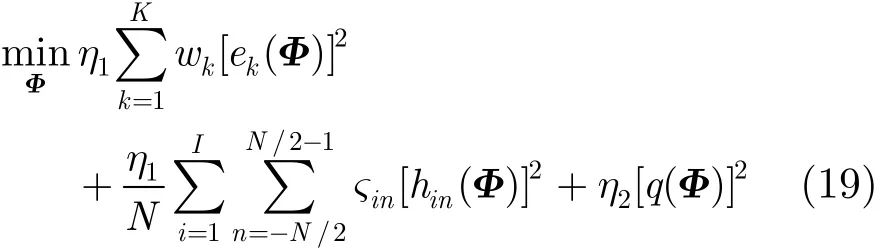
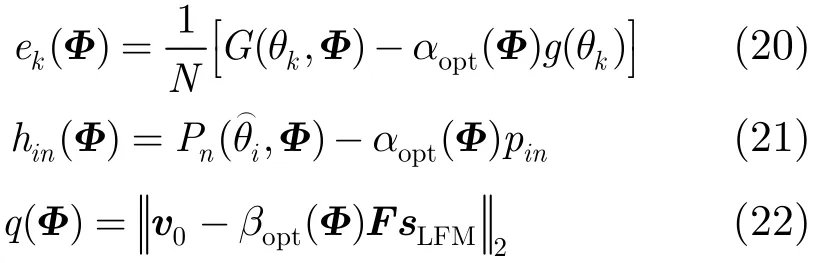
其中式(19)是相位矩阵Φ的无约束优化问题，由于非凸性，无法保证其最优解。但式(19)是四阶三角多项式，文献[15]中指出四阶三角多项式目标函数的局部最优解是全局最优解的1/2近似。另外，由于相位矩阵的维数可能较大，代价函数的Hess矩阵或近似Hess矩阵的计算复杂度比较高，因此本文采用基于波形相位矩阵的一阶梯度信息对波形进行优化设计。

式(19)中的目标函数关于相位矩阵的梯度为

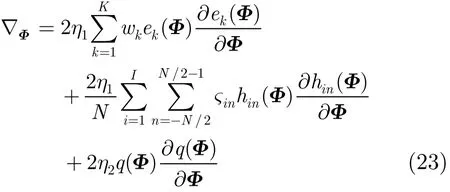
对于方向图逼近和功率谱逼近，其波形模型式(14)的代价函数关于波形相位矩阵的梯度即为式(23)前两项之和。式(23)中的ek(Φ),hin(Φ),q(Φ)包含由相位矩阵Φ构成的波形exp(jΦ)，其关于相位矩阵Φ的梯度可由链式法则容易求得。由于共轭梯度算法具有适中的计算复杂度和收敛速率，因此本文采用共轭梯度法求解波形设计问题式(14)及式(19)，其具体流程如表1所示。

该算法的主要计算量为目标函数C(Φ,α,β)及其梯度∇Φ的计算。在每次迭代中，计算C(Φ,α,β)的复杂度为O((K+I+1.5log2L)ML)，梯度∇Φ需要的计算复杂度约为O((4K+4I+4.5log2(L))ML)，因此每次迭代中计算复杂度约为O((5K+5I +6log2(L))ML)。

4 仿真实验

设一MIMO雷达系统包含M=16个发射阵元，阵元间距为半波长，发射的基带信号为相位编码信号，信号载频为fc=2 GHz ，假设所需的最大信号带宽为B=200 MHz ，阵元间距为d=c/2(fc+B/2)，离散化方位角总数为K=181，离散方位角间隔为1°，假设I=3个目标分别位于−40°,0°, 40°。方向图逼近权重和功率谱逼近权重会影响所设计波形的方向图和功率谱的性能，可以根据实际需求和侧重的不同设置不同权重。本文除特殊说明外，根据经验取权重为wk=1, k=1,2,…,K ,ςin=1,i=1,2,…,I ,n=1,2,…,N，另外，对于频谱逼近的权重设定为η=1。期望方向图由传统波束的主瓣构成，其中传统波束采用30 dB切比雪夫权，终止阈值为ε=10−3。

表1 波形设计算法流程

首先假设在−40°,0°方向的波束对两个目标分别进行跟踪且已知其多普勒频率，可在这两个波束方向采用相位编码信号，设信号带宽为B=10 MHz，信号时宽Tp=20 μs ，发射信号码长为BTp=200，为了得到低旁瓣的自相关特性，设置两个方向信号的期望功率谱为1; 40°方向的波束为搜索波束，需采用LFM信号，信号带宽为5 MHz，调频率为500 GHz/s，因此期望LFM信号的时宽为10 μs，即40°方向的信号时宽仅为发射信号总时宽的一部分。所设计波形的方向图如图2(a)所示，可以看出所设计波形在−40°,0°,40°方向形成3个波束，且逼近期望方向图。为了说明40°方向信号与期望LFM信号的逼近程度，图2(b)给出了所设计信号与期望信号的幅频特性，在带宽覆盖范围内幅频特性具有较好的逼近效果。图2(c)为−40°和0°方向信号的功率谱，所设计波形的功率谱与期望功率谱较接近。3个主波束方向信号的相关特性如图3所示，其中图3(a)为自相关特性，可以看出−40°,0°方向的信号具有较低的自相关旁瓣电平(约-29 dB)，40°方向信号的自相关旁瓣电平为-13.4 dB，与LFM信号自相关特性一致。图3(b)为互相关特性，3个主波束方向的信号具有较低的互相关峰值旁瓣电平(约-15 dB)。图4所示为模糊函数的比较图，其中图4(a)为所设计信号的模糊函数，图4(b)为期望LFM信号的模糊函数，比较图4(a)和4(b)可以看出所设计信号具有期望的模糊函数形状。如图5所示，目标函数值(20次随机初始化)随迭代次数的增加而递减，并逐渐趋于平稳。

图2 波形的空域和频域特性

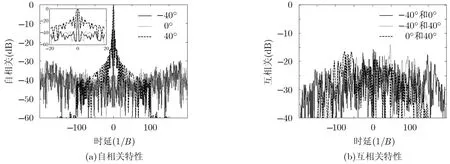
图3 各方向信号相关特性

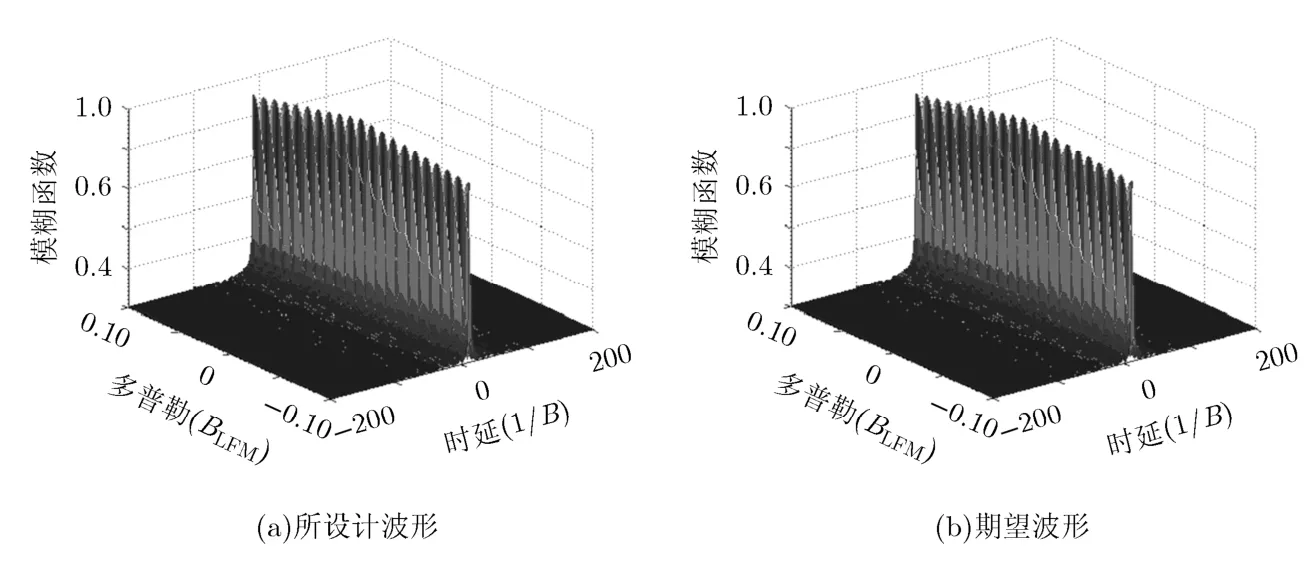
图4 模糊函数

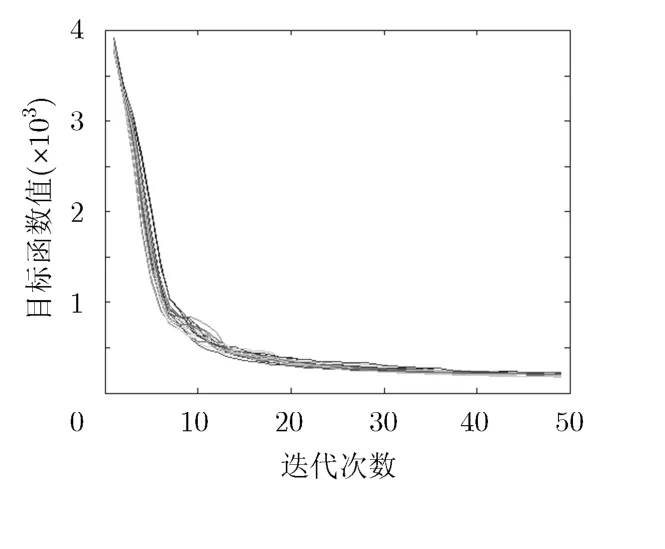
图5 目标函数值随迭代次数的变化曲线

另外，假设需在3个方向上分别产生宽带信号、低自相关旁瓣的窄带相位编码信号和LFM信号，宽带信号带宽为B=200 MHz, LFM调频信号带宽为BLFM=10 MHz，为了得到低的自相关旁瓣，以加Hamming窗的LFM信号功率谱作为窄带相位编码信号的期望功率谱，加窗前LFM信号的带宽为80 MHz。发射信号脉冲宽度为Tp=2.56 μs，因此基带信号的码长可取为L=TpB=512。另外，设−40°方向上存在两个干扰频段[1.9101.920] GHz和[1.959 1.969] GHz，为了抑制干扰可在此频段产生凹口。因此设置−40°方向信号的期望功率谱在此频段为0，其余区域为1，设置零陷处功率谱逼近权重为20。图6(a)所示为所设计信号的方向图，在期望的3个方向上形成了较理想的波束。图6(b)为40°方向信号与期望LFM信号的幅频特性比较图，所设计信号在40°方向具有期望的频谱特性。图6(c)给出了−40°和0°方向信号的功率谱，实现了期望功率谱形状，−40°方向的功率谱在干扰频段产生了约10 dB的凹口，0°方向信号具有加窗的功率谱形状。图7(a)所示为所设计波形在各方向的功率谱，结合图6(c)，可以看出3个主瓣方向信号具有不同的功率谱，−40°方向信号功率谱覆盖了除干扰频段外的频段，0°方向信号功率谱分布于载频附近。图7(b)为3个主瓣方向信号的自相关特性，−40°方向信号具有高的分辨力，0°方向信号的自相关函数具有较低的峰值旁瓣电平，约为-36.5 dB, 40°方向信号的自相关特性与期望LFM信号的自相关特性一致。3个主瓣方向的互相关特性与图3(b)类似(未给出)，峰值互相关电平约为-15.2 dB。图8所示为40°方向信号的模糊函数，其中图8(a)为所设计信号的模糊函数，图8(b)为期望LFM信号的模糊函数，比较图8(a)和8(b)可以看出所设计信号具有期望的模糊函数形状。图9所示为目标函数值(20次随机初始化)随迭代次数的变化曲线，与图5的效果类似。

值得注意的是，为了实现波束扫描，可以采用前一波位的波形进行初始化，根据期望方向图的指向变化，优化所需波形。此外，文中采用发射多波束，需要对回波中各目标的回波数据进行分离：可以同时形成多个接收波束，分别指向发射波束的方向，从空域将来自其他方向的信号滤除；另外由于不同方向的信号不同，相关性较小，经过匹配滤波后，也可以对其他方向的回波信号进行抑制。

5 结论

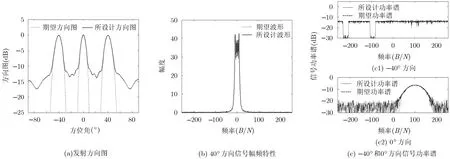
图6 波形的空域和频域特性

图7 功率谱与自相关函数

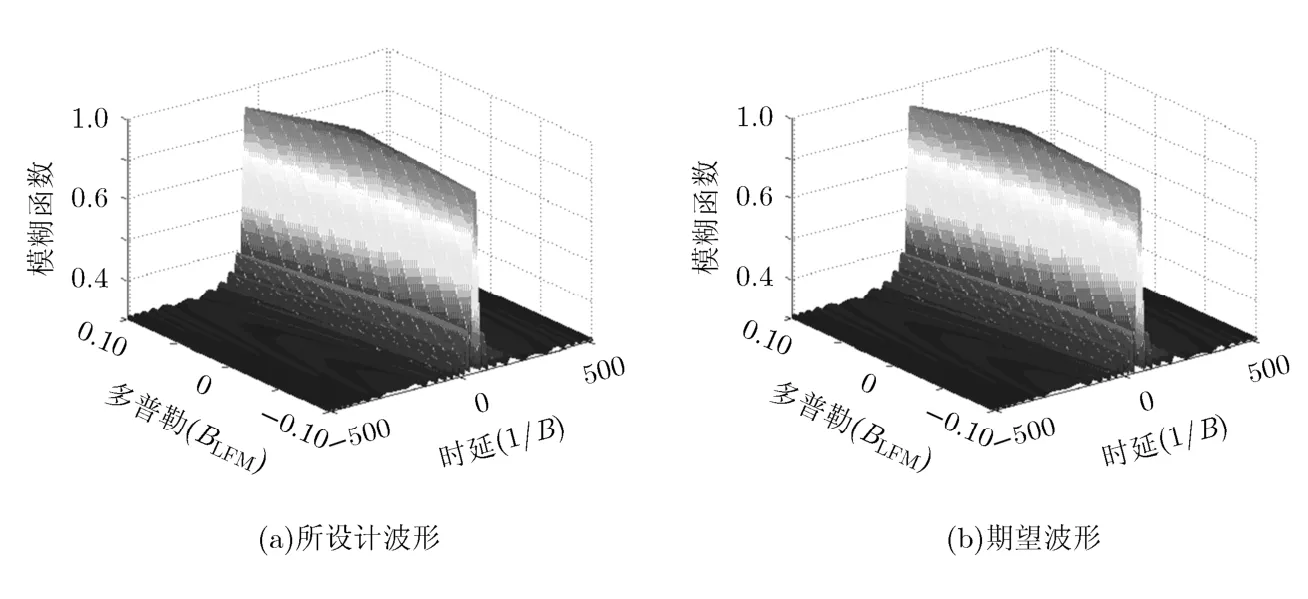
图8 模糊函数

图9 目标函数值随迭代次数的变化曲线

MIMO雷达各发射天线具有发射不同信号的能力，可以灵活地进行发射波形设计，以采用不同模式满足不同需求、功能。本文提出一种MIMO雷达多模式波形设计方法，该方法以方向图逼近、波束指向方向信号功率谱逼近及频谱逼近等为准则，通过建立关于波形相位矩阵的多目标优化模型对发射波形进行优化，在空域上可以形成多个波束，不同波束指向上信号可以具有不同特性，以分别实现不同功能。

[1] Haimovich A M, Blum R S, and Cimini L J. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116-129.

[2] Li J and Stoica P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106-114.

[3] Duly A J, Love D J, and Krogmeier J V. Time-division beamforming for MIMO radar waveform design[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1210-1223.

[4] Lipor J, Ahmed S, and Alouini M S. Fourier-based transmit beampattern design using MIMO radar[J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2226-2235. [5] Fuhrmann D R and Antonio G S. Transmit beamforming for MIMO radar systems using signal cross-correlation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 171-186.

[6] Stoica P, Li J, and Xie Y. On probing signal design for MIMO radar[J]. IEEE Transactions on Signal Processing, 2007, 55(8): 4151-4161.

[7] Ahmed S, Thompson J S, and Petillot Y, et al.. Unconstrained synthesis of covariance matrix for MIMO radar transmit beampattern[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3837-3849.

[8] 罗涛, 关永峰, 刘宏伟, 等. 低旁瓣MIMO 雷达发射方向图设计[J]. 电子与信息学报, 2013, 35(12): 2815-2822.

Luo Tao, Guan Yong-feng, Liu Hong-wei, et al.. Low sidelobe transmit pattern design for MIMO radar[J]. Journal of Electronics & Information Technology, 2013, 35(12): 2815-2822.

[9] Hua G and Abeysekera S S. MIMO radar transmit beampattern design with ripple and transition band control[J]. IEEE Transactions on Signal Processing, 2013, 61(11): 2963-2974.

[10] Stoica P, Li J, and Zhu X. Waveform synthesis for diversity-based transmit beampattern design[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2593-2598.

[11] Ahmed S, Thompson J S, Petillot Y, et al.. Finite alphabet constant-envelope waveform design for MIMO radar[J]. IEEE Transactions on Signal Processing, 2011, 59(11): 5326-5337.

[12] 胡亮兵, 刘宏伟, 杨晓超, 等. 集中式MIMO雷达发射方向图快速设计方法[J]. 电子与信息学报, 2010, 32(2): 481-484.

Hu Liang-bing, Liu Hong-wei, Yang Xiao-chao, et al.. Fasttransmit beampattern synthesis for MIMO radar with colocated antennas[J]. Journal of Electronics & Information Technology, 2010, 32(2): 481-484.

[13] 罗涛, 关永峰, 刘宏伟, 等. 平面阵MIMO雷达发射方向图设计方法[J]. 电子与信息学报, 2013, 35(11): 2707-2713.

Luo Tao, Guan Yong-feng, Liu Hong-wei, et al.. Transmit beampattern design for planar array MIMO radar[J]. Journal of Electronics & Information Technology, 2013, 35(11): 2707-2713.

[14] Ahmed S and Alouini M S. MIMO radar transmit beampattern design without synthesising the covariance matrix[J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2278-2289.

[15] Wang Y C, Wang X, Liu H W, et al.. On the design of constant modulus probing signals for MIMO radar[J]. IEEE Transactions on Signal Processing, 2012, 60(8): 4432-4438.

[16] Skolnik M I. Radar Handbook[M]. 3rd Edition, Boston, Massachusetts: McGraw-Hill, 2008, Chaper 1.

[17] 林锉云, 董加礼. 多目标优化的方法与理论[M]. 吉林: 吉林教育出版社, 1992: 55-82.

Lin Cuo-yun and Dong Jia-li. Multi-objective Optimization Method andTheory[M]. Jilin: Jilin Press of Education, 1992: 55-82.

王 旭： 男，1987年生，博士生，研究方向为MIMO雷达、认知雷达发射波形设计.

刘宏伟： 男，1971年生，博士，教授，博士生导师，研究方向为雷达信号处理、雷达自动目标识别、认知雷达、协同探测等.

纠 博： 男，1982年生，博士，副教授，研究方向为自适应信号处理、雷达自动目标识别、认知雷达.

Multi-modes Waveform Optimization Design Method for MIMO Radar

Wang Xu Liu Hong-wei Jiu Bo Wu Meng Bao Zheng
(National Laboratory of Radar Signal Processing, Xidian University, Xi'an 710071, China)

In the scenario of multiple targets and multiple tasks, radar should have multiple functions to realize different modes, such as search and tracking. Traditional radar can only implement one function and the working mode is not flexible, which may result in inefficient use of the system resources. In this paper, a MIMO radar waveform design method is proposed to realize multiple modes. Based on the criterions of beampattern matching, power spectrum matching in the desired direction or frequency spectrum matching, a multi-objective optimization model for the waveform matrix with constant modulus constraint is established, and is solved by the conjugate gradient method. The numerical results show that the optimized waveforms have multiple beams and different modes in the beam directions, which can simultaneously realize search, tracking and so on.

MIMO radar; Waveform design; Transmit beampattern; Multiple beams; Multiple functions

TN958

： A

：1009-5896(2015)06-1416-08

10.11999/JEIT141179

2014-09-10收到，2014-11-26改回

国家自然科学基金(61271291, 61201285)，新世纪优秀人才支持计划(NCET-09-0630)，全国优秀博士学位论文作者专项资金(FANEDD-201156)，国家部委基金和中央高校基本科研业务费专项资金资助课题

*通信作者：纠博 bojiu@mail.xidian.edu.cn