基于几何校正的聚束SAR快速分级后投影算法
左绍山杨泽民 孙光才 邢孟道
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
基于几何校正的聚束SAR快速分级后投影算法
左绍山*杨泽民 孙光才 邢孟道
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
快速分级后投影(Fast Factorized Back Projection, FFBP)算法大幅减少了原始后投影算法的插值次数,提升运算效率。然而图像合成过程中仍然需要大量的图像域2维插值操作,庞大的计算量限制了其在实际中的应用。该文提出一种基于几何校正的聚束SAR快速分级后投影算法。该算法利用几何校正的方法实现子图像配准,即在满足聚焦性能的前提下,通过距离维平移和角度维旋转完成子图像在不同坐标系下的投影和子图像合成。该算法避免了逐点插值运算,进一步降低了FFBP算法的计算量。仿真结果表明,该算法能高精度聚焦成像,并且其运算效率相对于基于图像域2维插值的FFBP算法显著提高。
SAR;聚束;快速分级后投影;几何校正;逐点插值
1 引言
合成孔径雷达是一种全天候、全天时遥感设备,自20世纪50年代出现以来,研究人员提出了多种SAR成像算法[1,2]。其中,后向投影(Back Projection, BP)算法由于其能够适用于SAR的任意工作模式,能够对含有运动误差的任意成像几何的SAR数据进行精确聚焦[3]并且容易采用并行计算实现[4]而受到人们的关注。最初,BP算法是从计算机层析成像[5−8]领域引入的。1983年,文献[6]将其用于聚束SAR成像。然而BP算法需要逐点遍历,计算量大,效率低。比如,当图像为N×N点,孔径长度也为N时,整个成像过程需要3N次插值操作[9]。庞大的计算量限制了BP算法的实践应用。为了降低BP算法的运算量,人们进行了很多研究[10−19]。文献[10]提出了一种快速后投影(Fast Back Projection, FBP)算法。当分块大小取为N时,该算法计算量达到理论最优的O(N2.5)。相对于BP算法,该算法计算量有所减少,但是在实际应用中,算法效率仍然不高。文献[16]提出了一种利用波数域谱融合的快速BP算法。一些研究人员提出了将自聚焦方法与后投影相结合的成像算法[17−18]。文献[19]提出了快速分级后投影(Fast Factorized Back Projection, FFBP)算法。这种算法首先划分子孔径得到粗分辨率的子图像,然后子图像逐级相干累加得到全分辨率图像。当基数取2或4时,快速分级后投影算法计算量达到理论最优的O(N2log2N)。然而快速分级后投影算法FFBPA需要2维逐点插值,并且多次迭代操作使得算法流程比较繁琐。在实际应用时,FFBP算法需要选取较长的子孔径,或取较大的基数以降低迭代次数,获得较好的聚焦效果。也就是说,FFBP算法难以达到O(N2log2N)的计算量。
针对FFBP算法2维逐点插值计算量大的问题,本文提出的基于几何校正的FFBP算法对子图像的每行每列进行整体操作,避免2维逐点插值运算,提高了计算速度并且处理流程简单方便。本文首先分析了快速分级后投影算法,给出了成像模型,然后详细介绍了基于几何校正的FFBP算法的原理和实现步骤,接下来分析了本文所提算法的误差和计算量,最后通过仿真实验验证本算法的有效性。
2 快速分级后投影算法
文献[10]证明了,在初始孔径很短时,极坐标系格式下的数据在角频域只占很窄的一部分区域,这意味着在比较粗糙的分辨率下进行成像而不损失图像信息。因此FFBP算法以及本文提出的算法都是在局部极坐标系(Local Polar Coordinates, LPC)下实现成像。本文针对聚束SAR成像模式进行研究讨论。局部极坐标系聚束SAR成像几何如图1所示。

图1 极坐标系下聚束SAR成像几何
图1中,L表示子孔径长度,X轴表示飞机航迹。以子孔径的中心O为原点,建立LPC,极轴垂直航迹并指向成像场景一侧,如图1中虚线所示,规定极轴右侧角度为正值,极轴左侧角度为负值。场景中任意一点P,其在该LPC中的坐标为(rp,θp)。在某时刻,雷达在LPC中的坐标为(X, π/2)。根据余弦定理,可得P点到雷达的瞬时斜距R(X,rp,θp):

设雷达发射信号为sT(τ),其带宽为B,波长为λ。则接收到的目标回波为
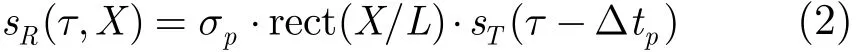
其中,σp表示目标P点的后向散射系数,时延Δtp, c表示光速。sR(τ,X)经过脉冲压缩处理得到
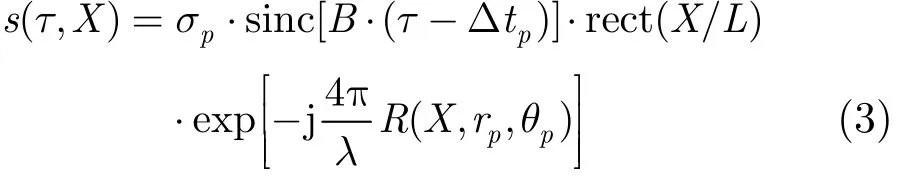
FFBP算法首先利用传统BP积分模型对子孔径信号进行成像处理,BP算法在时域将距离脉冲压缩后的数据后向投影到各成像点,通过相干积累得到聚焦的图像。子孔径BP积分过程可表示为

FFBP算法的主要思想是:先将全孔径划分成若干子孔径,再利用BP积分分别对子孔径信号成像处理,得到多幅粗分辨率的子图像,然后采用多级合成,逐级提高图像分辨率,最终得到全分辨率图像。FFBP算法避免了对成像场景中每个点在全孔径搜索的过程[3],相对于BP算法,减少了计算量,提高了运算效率。然而在子图像合成过程中,FFBP算法需要图像域2维逐点插值。如图2所示,在某一级子图像合成过程中,令子图像I1(如图2(a)所示),所在局部极坐标系为LPC1,如图2中细实线部分所示。子图像I2(如图2(c)所示)所在局部极坐标系为LPC2,如图2中虚线部分所示。设点P在 LPC1中的坐标为(r1,θ1),在LPC2中的坐标为(r2,θ2)。
在图2中,由于P点在不同子图像中的位置不相同,FFBP算法在子图像合成过程中,需要分别在子图像I1和子图像I2中查找P点的位置(r1,θ1)和(r2,θ2)。为提高取点精度,需要图像域2维插值操作。这在实际应用中计算量很大,计算效率不高。为进一步提升运算效率,本文提出的基于几何校正的FFBP算法通过对子图像进行几何校正实现子图像配准,避免了2维逐点插值运算,下面具体介绍。

图2 叠加前子图像及子图像叠加前后局部极坐标系几何关系图
3 基于几何校正的快速分级后投影算法
如图2所示,P点在合成后的LPC(令为LPCr,如图2中粗实线部分所示)中的坐标为(r,θ),那么P点从LPC1到LPCr的投影过程中的位置偏移量为(Δr,Δθ),其中距离偏移量Δr=r1−r ,角度偏移量Δθ=θ1−θ。几何校正示意图如图3所示。
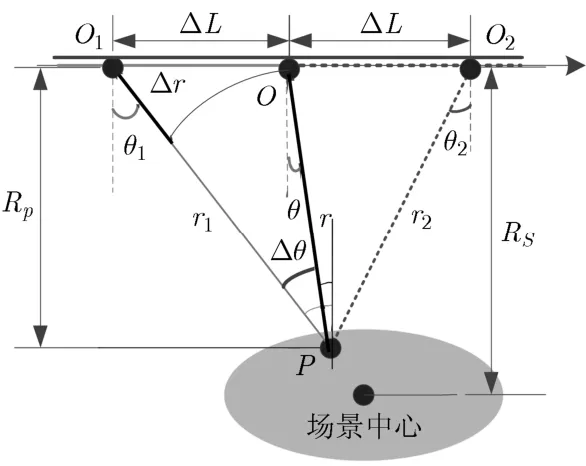
图3 几何校正示意图
图3中,RS为场景中心到航线的距离,Rp为P点到航线的垂直距离。ΔL为LPC1的坐标原点到LPCr原点的距离。
根据余弦定理,可得
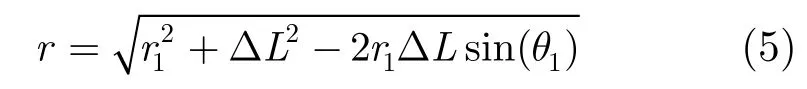
将式(5)进行泰勒级数展开,并忽略ΔL三次及以上的高次项,得到

从式(6)可以看出,距离维平移量Δr=Δr(r1,θ1)是2维空变的,这也是FFBP需要逐点操作的原因。本文采用一定的近似(近似误差见第4节)进行降维,令r1≈RS,则距离维平移量可表示为
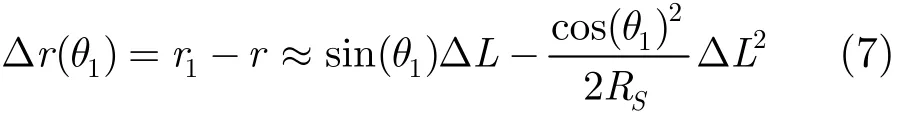
在角度维,根据图3中坐标系几何关系,可得

化简可得
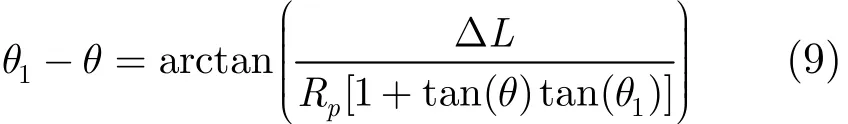
从式(9)可以看出,角度旋转量也是2维的,对远场SAR成像来说,某LPC的角度因此令 Rp≈r,则式(9)可表示为
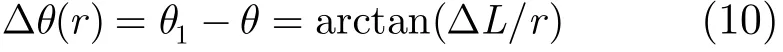
综上所述,2维(距离维和角度维)空变的距离平移量和角度旋转量,如式(6)和式(9),经过相应的近似计算变为1维空变,即距离维平移量只与角度维有关系,如式(7)所示,角度维旋转量只和距离维有关系。假设子图像矩阵(极坐标系下)的列表示距离维,行表示角度维,这样距离维平移就可以逐列进行,角度维旋转就可以逐行进行。而子图像矩阵的平移旋转操作可以通过FFT,线性相位相乘以及IFFT实现。
经过距离平移和角度旋转后,子图像I1已投影至LPCr中,同理也可将子图像I2投影至LPCr中。需要注意的是,为了避免角度维模糊,在子图像相干叠加前需要对子图角度维进行两倍上采样。这样就完成了子图像的几何校正,几何校正步骤如图4所示。

图4 子图像几何校正流程图
下面给出本文算法的具体操作步骤。算法流程图(以4个子孔径为例)如图5所示。

图5 算法流程图
(1)划分子孔径,并以每个子孔径的中心为原点,建立各自的LPC。利用BP算法在LPC下对子孔径信号进行成像,得到粗分辨率子图像;
(2)对粗分辨率的子图像分级进行几何校正和相干叠加。在每一级处理中,根据式(7)和式(10)计算子图像的距离平移量和角度旋转量,并在角度维上采样,完成对子图像的几何校正,然后子图像相干叠加;如此重复,逐级合成,直至得到极坐标系下全分辨率的图像;
(3)将极坐标系下的全分辨率图像转换到直角坐标系。
4 误差分析
在进行几何校正过程中,偏移量的推导采用了近似计算。下面对近似误差进行分析。
在距离维,由于采用r1≈RS,距离偏移量误差
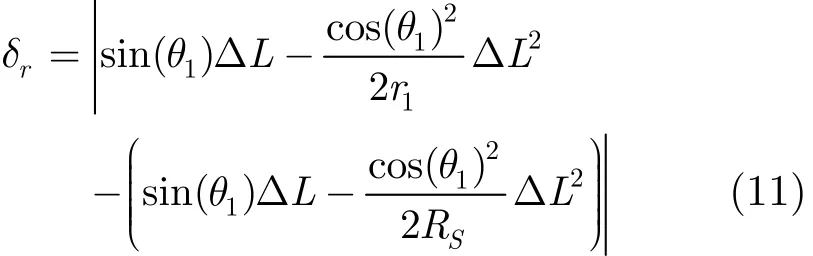
考虑到ΔL≤La/4, La表示全孔径长度,La= λRS/(2ρa)。另外,由图2 中LPC几何关系图可知,LPC1中的极半径r1≥RS−Wr/2, Wr为场景距离维宽度,cos(θ1)2≤1,则式(11)可化简为

在距离维,为了获得良好的聚焦效果,要求距离偏移量误差δr≤ρr/4,即

整理可得

在角度维,角度旋转误差为
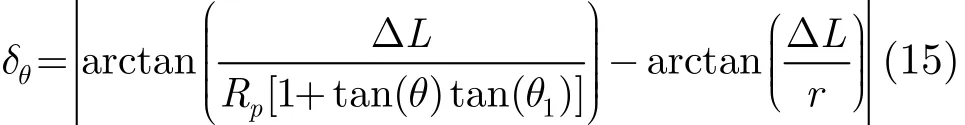
根据图2几何关系图,可知Rp=rcos(θ)。由于和ΔL/r都很小,且,则式(15)可以表示为

考虑到极坐标系中,角度的范围如式(17)
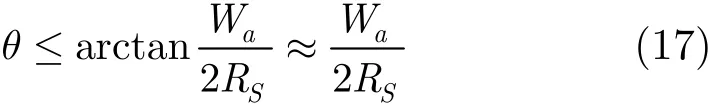
则式(16)可以化简为

为了在角度维获得良好的聚焦效果,要求角度旋转误差δθ≤ρθ/4,其中,ρθ表示角度分辨率,ρθ=ρa/(4RS),则式(18)可表示为
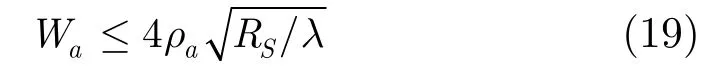
通过式(14)和式(19)可以看出,在聚束模式下,采用几何校正方法进行成像,场景观测范围受到限制。
5 计算量分析对比
在聚束模式下,假设图像大小为N×N(距离维×角度维),脉冲压缩后的数据有N个脉冲,将全孔径划分为n个子孔径,则总共需要log2n级合成。本算法第(1)步通过BP算法获得粗糙子图像的计算量为N3。算法在第i,i=1,2,…,log2n级合成过程中,主要处理步骤有:距离维FFT,距离维线性相位相乘和距离维IFFT;角度维FFT,角度维线性相位相乘,补零,角度维IFFT等。由于线性相位相乘和补零运算的计算量远小于FFT和IFFT的计算量,可以忽略不计。在第i,i=1,2,…,log2n级,需要处理的子图像共有n/2i−1个,每个子图像大小为N×(2i−1N)/n (距离维×角度维),则距离维FFT计算量为N2log2N,距离维IFFT计算量为N2log2N,角度维FFT计算量为N2log2(2i−1N/n),角度维IFFT的计算量为2N2log2(2iN/n),第i级合成总的计算量为C(i)=5N2log2N−3N2log2n+(3i−1)N2。因此,本文算法总的计算量为

对于相同的数据,FFBP算法第(1)步成像的计算量也为N3。在子图像合成过程中,如果在距离维和角度维采用4倍临近点FFT插值,FFBP算法总的计算量为CFFBP=N3+(10log2N+27/2)N2log2n−(5/2)N2(log2n)2。由于N≥n≥1且N,n都是正整数,因此CFFBP−C=(5log2N+13)N2log2n −N2(log2n)2>0恒成立。可见,相对于基于2维逐点插值的FFBP算法本方法降低了计算量。
6 仿真
为了验证本算法的有效性,本节给出仿真数据处理结果。本仿真是在机载聚束模式下对场景中的9个点目标进行的成像仿真实验,仿真场景为3×3的矩形点阵。各点目标编号如下:第1行3个目标编号为1~3,第2行3个点目标编号为4~6,第3行3个点目标编号为7~9,如图6所示。雷达发射窄脉冲脉冲重复频率900 Hz,采样频率600 MHz,利用表1中的参数仿真回波数据。最终图像理论分辨率为0.3 m×0.3 m(距离向×方位向),图像采样间隔为0.25 m×0.25 m(距离向×方位向)。

表1 仿真参数
仿真成像结果如图7所示。选取编号为1的点目标(图7中圆圈内的点)进行聚焦性能分析,其等高线图如图8(a)所示,散布函数的包络如图8(b)、图8(c)所示。
图7中水平方向为方位向,垂直方向为距离向。从图7可见成像结果和仿真所用的矩形点阵(图6)相吻合。图8(a)为目标1的等高线图,其水平方向为方位向,垂直方向为距离向。从图8(b)和图8(c)可看出散布函数包络规整,距离向和方位向都采用32倍插值,通过计算主瓣−3 dB宽度得到方位分辨率为0.27 m。表2给出了目标1的积分旁瓣比(ISLR)和峰值旁瓣比(PSLR)。ISLR和PSLR的值也都在理论值(ISLR大约为−9.8 dB, PSLR大约为−13.26 dB )附近。这表明本文算法聚焦性能良好。

表2 聚焦性能指标(dB)
对相同的仿真数据分别采用本文算法和FFBP算法在同一台电脑上进行处理。其中,数据大小为8192×8192(方位×距离),电脑配置为Intel(R) Core(TM) i5-3570 CPU@3.40 GHz, RAM 4.00 GB。子孔径个数分别为8, 16, 32, 64和128时,两种算法的处理时间(由于电脑配置、程序优化等影响,处理时间会有差异)如图9所示。从图9可以看出,在本仿真中,两条曲线都呈现下降趋势,但是本文提出的算法处理时间比较短。
通过仿真可知,本文算法成像质量良好,并且相对于FFBP算法,本文算法处理时间短,处理效率明显提高。
7 结束语
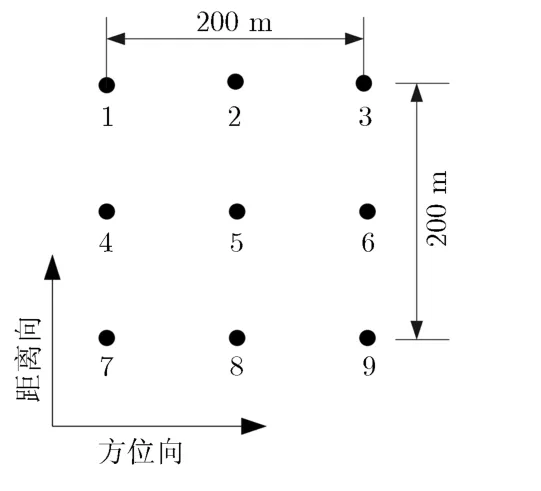
图6 场景布点示意图
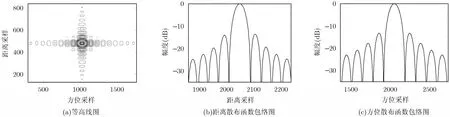
图8 本文算法成像性能分析

图9 处理时间对比
本文提出了一种针对聚束模式的基于几何校正的快速分级后投影算法,该算法通过基于FFT的距离维平移和角度维旋转实现子图像配准合成。相对于2维逐点插值运算,该方法计算量小,效率高并且处理方便简单。然而由于距离平移量和角度旋转量是通过近似计算得到的。为了满足成像质量要求,成像场景的范围受到限制。提高距离平移量和角度旋转量的精度,扩大场景范围并将其推广应用到其他成像模式需要进一步研究。
[1] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 2-6.
[2] Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Norwood, MA: Artech House, 2005: 308-319.
[3] 杨泽民, 孙光才, 吴玉峰, 等. 一种新的基于极坐标格式的快速后向投影算法[J]. 电子与信息学报, 2014, 36(3): 537-544.
Yang Ze-min, Sun Guang-cai, Wu Yu-feng, et al.. A new fast back projection algorithm based on polar format algorithm [J]. Journal of Electronics & Information Technology, 2014, 36(3): 537-544.
[4] Ozsoy S and Ergin A. A pencil back projection method for SAR imaging[J]. IEEE Transactions on Image Processing, 2009, 18(3): 573-581.
[5] Scudder H J. Introduction to computer aided tomography[J]. Proceedings of the IEEE, 1978, 66(6): 628-637.
[6] Munson D C, Jr O'Brien J D, and Jenkins W K. A tomographic formulation of spotlight mode synthetic aperture radar[J]. Proceedings of the IEEE, 1983, 71(8): 917-925.
[7] Desai M D and Jenkins W K. Convolution back-projection image reconstruction for spotlight mode synthetic aperture radar[J]. IEEE Transactions on Image Processing, 1992, 1(4): 505-516.
[8] Wang Yi-duo, Xi Ping, and Xue Wei. Fast filter back projection algorithm based on hexagonal grid[C]. International Conference on Electrical and Control Engineering, Wuhan, China, 2010: 964-969.
[9] Xiao S, Munson D C Jr, and Basu S. An N2logN backprojection algorithm for SAR image formation[C]. Conference Record of the Thirty-Fourth Asilomar Conference on Signals Systems and Computers, Pacific Grove, CA, USA, 2000, 1: 3-7.
[10] Yegulalp A F. Fast back-projection algorithm for synthetic aperture radar[C]. The Record of the 1999 IEEE Radar Conference, Waltham, MA, USA, 1999: 60-65.
[11] 陈思, 赵惠昌, 张淑宁, 等. 基于dechirp弹载SAR的改进后向投影算法[J]. 物理学报, 2013, 62(21): 1-9.
Chen Si, Zhao Hui-chang, Zhang Shu-ning, et al.. An improved back projection imaging algorithm for dechirped missile-borne SAR[J]. Acta Physica Sinica, 2013, 62(21): 1-9.
[12] Durand R, Ginolhac G, and Thirion-Lefevre L. Back projection version of subspace detector SAR processors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1489-1497.
[13] 庞礴, 代大海, 邢世其, 等. SAR层析成像技术的发展和展望[J]. 系统工程与电子技术, 2013, 35(7): 1421-1429.
Pang Bo, Dai Da-hai, Xing Shi-qi, et al.. Development and perspective of tomographic SAR imaging technique[J]. Systems Engineering and Electronics, 2013, 35(7): 1421-1429.
[14] 张文彬, 邓云凯, 王宇, 等. 星地双基合成孔径雷达聚束模式快速BP算法[J]. 雷达学报, 2013, 2(3): 357-366. Zhang Wen-bin, Deng Yun-kai, Wang Yu, et al.. A fast backprojection algorithm for spotlight mode Bi-SAR imaging [J]. Journal of Radars, 2013, 2(3): 357-366.
[15] Vu V T, Sjogren T K, and Pettersson M I. SAR imaging in ground plane using fast backprojection for mono-and bistatic cases[C]. 2012 IEEE Radar Conference, Atlanta, USA, 2012: 184-189.
[16] Zhang Lei, Li Hao-lin, and Qiao Zhi-jun. A fast BP algorithm with wavenumber spectrum fusion for high-resolution spotlight SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(9): 1460-1464.
[17] 高阳, 禹卫东, 冯锦, 等. 一种基于勒让德拟合的SAR后向投影自聚焦算法[J]. 雷达学报, 2014, 3(2): 176-182.
Gao Yang, Yu Wei-dong, Feng Jin, et al.. A SAR back projection autofocusing algorithm based on Legendre approximation[J]. Journal of Radars, 2014, 3(2): 176-182.
[18] 张磊, 李浩林, 邢孟道, 等. 快速后向投影合成孔径雷达成像的自聚焦方法[J]. 西安电子科技大学学报(自然科学版), 2014, 41(1): 69-74.
Zhang Lei, Li Hao-lin, Xing Meng-dao, et al.. Autofocusing the synthetic aperture radar imagery by the fast backprojection algorithm[J]. Journal of Xidian University(Natural Science), 2014, 41(1): 69-74.
[19] Ulander L M H, Hellsten H, and Stenstrom G. Syntheticaperture radar processing using fast factorized backprojection[J]. IEEE Transactions on Aerospace Electronic Systems, 2003, 39(3): 760-776.
左绍山: 男,1988年生,博士生,研究方向为SAR成像.
杨泽民: 男,1988年生,博士生,研究方向为星载SAR成像.
孙光才: 男,1984年生,讲师,研究方向为SAR成像和动目标检测.
邢孟道: 男,1975年生,教授,博士生导师,研究方向为雷达成像和目标识别.
Geometric Correction Based Fast Factorized Back Projection Algorithm for Spotlight SAR Imaging
Zuo Shao-shan Yang Ze-min Sun Guang-cai Xing Meng-dao
(National Laboratory of Radar Signal Processing, Xidian University, Xi'an 710071, China)
Compared with the Back Projection Algorithm (BPA), the interpolation load of the Fast Factorized Back Projection Algorithm (FFBPA) is released. However, the 2D interpolation in the image domain is essential for the FFBPA and the intensive computational burden limits its application in practice. This paper presents the geometric correction based FFBPA for the spotlight SAR imaging. In this algorithm, the sub-image registration is accomplished by the geometric correction method that the sub-image projection in the different coordinate systems and sub-image fusion are fulfilled by the shift in the range dimension and the rotation in the angle dimension. Thus the method avoids the individual interpolation and it is more efficient than the FFBPA. Simulation results validate its imaging performance and efficiency.
SAR; Spotlight; Fast Factorized Back Projection Algorithm (FFBPA); Geometric correction; Individual interpolation
TN957.51
: A
:1009-5896(2015)06-1389-06
10.11999/JEIT141254
2014-09-26收到,2015-02-09改回
国家自然科学青年基金(61301292)和教育部博士点基金(20130203120007)资助课题
*通信作者:左绍山 zuoshaoshan@126.com

