5×135 气动马达动平衡分析与曲轴改进

王景祥，郭浩，郭志平，谢志强

（1.内蒙古工业大学机械学院，内蒙古 呼和浩特 010051；2.苏州大学机器人与微系统研究中心，江苏 苏州 215021）

0 引言

山东泰安巨菱钻探装备有限责任公司生产的气动载人绞车通过5×135 气动马达作为动力传动机构来完成绞车的载人工作。 5×135 气动马达将高压气体通过配气阀和分配阀依次传递到五个气缸内，高压气体到达气缸后迅速膨胀产生气体压力。 气体压力作用在活塞表面，再通过连杆将作用力传递到曲轴轴颈上，推动曲轴做旋转运动。 曲轴旋转一周，五个缸依次完成一个周期的工作。 由于气体压力最终都作用到曲轴上，因此在设计中，对曲轴进行合理的分析关系到马达的整体工作效率。一般将曲轴的动平衡作为主要的分析对象[1]。曲轴的不平衡量过大，会引起马达的振动，加快轴承等零部件的磨损，降低发动机的使用寿命[2]。 针对目前使用的气动马达存在的动不平衡问题，进行分析和改进，从三维建模软件UG 中可以完成三维模型的建立，得出实体的质量、质心、惯性矩等特征参数，在MATLAB 中计算得出分析数据[3]。

1 现有气动马达曲轴分析

1.1 现有气动马达动平衡计算

5×135 气动马达使用的是中心曲柄连杆机构，五个气缸通过各自的连杆同时作用在一个单拐曲轴上，成星形分布，如图1。 分析知，气动马达在工作工程中由于运动特性的原因，会产生往复惯性力和旋转惯性力[4]，这些惯性力是造成马达动不平衡的根本原因。

图1 马达气缸分布图

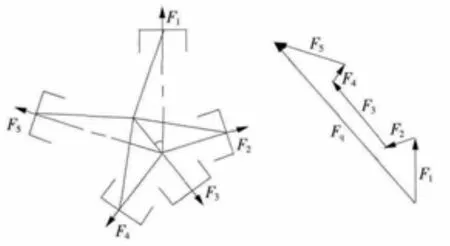
图2 矢量叠加图

往复惯性力是由往复运动的活塞组质量产生，作用在各个气缸的中心线上，分为一阶往复惯性力和二阶往复惯性力。由于5×135 气动马达的二阶往复惯性力仅为一阶的20%，设计时可不考虑[5]。 只对五个缸的一阶往复惯性力进行矢量叠加，叠加结构简图和结果如图2。

通过对矢量叠加图的分析知， 叠加后的一阶往复惯性力始终沿曲柄径向作用在曲轴轴颈上[6]。旋转惯性力是由曲柄组做旋转运动产生， 与往复惯性力作用在同一方向上。因此，往复惯性力和旋转惯性力可通过合理布置平衡块进行平衡[7]。动平衡计算中所使用结构简图如图3。

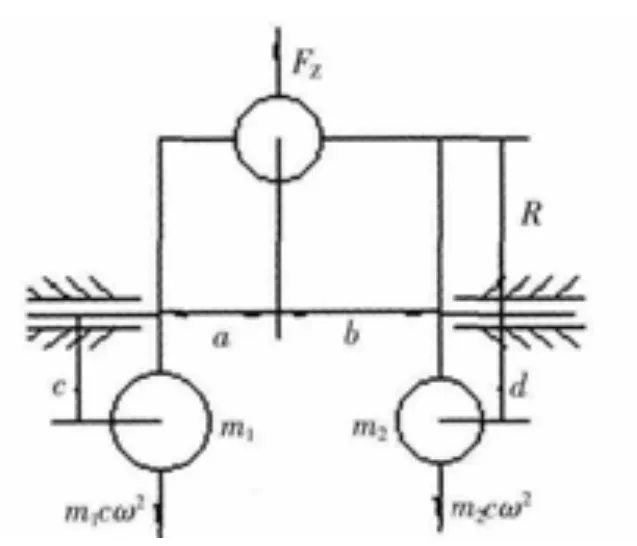
图3 动平衡计算结构简图

目前所用气动马达曲轴结构如图4 所示。

图4 现有曲轴结构

旋转曲轴的惯性力公式为：

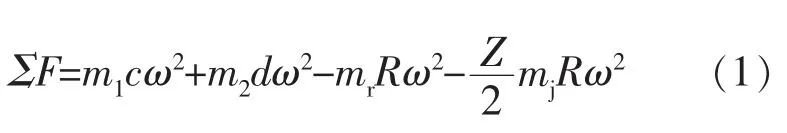
式中 ΣF——总的惯性力

mr——曲柄组质量

R——曲轴偏心距

ω——曲轴旋转角速度

Z——气缸数

mj——活塞组质量

m1——左侧平衡重质量

m2——右侧平衡重质量

c——左侧平衡重质心到曲轴旋转中心的距离

d——右侧平衡重质心到曲轴旋转中心的距离

曲轴偏心距R=0.038 m，气缸数Z=5，曲轴旋转角速度 ω=0－190 r/min。 在 UG 中分析得出：mj=1.758 kg，mr=5.53 kg，m1=4.048 kg，m2=3.389 kg，c=0.0405 m，d=0.0399 m。在 MATLAB 中计算得出曲轴旋转角速度与不平衡惯性力的关系如图5。

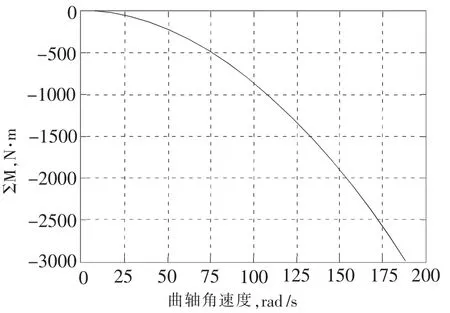
图5 惯性力与曲轴角速度的关系

两块平衡重在曲轴轴颈处产生的弯矩公式为：

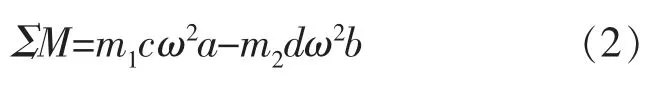
式中 ΣM——两块平衡重在轴颈上产生的弯矩

a——左平衡重距轴颈中心的距离

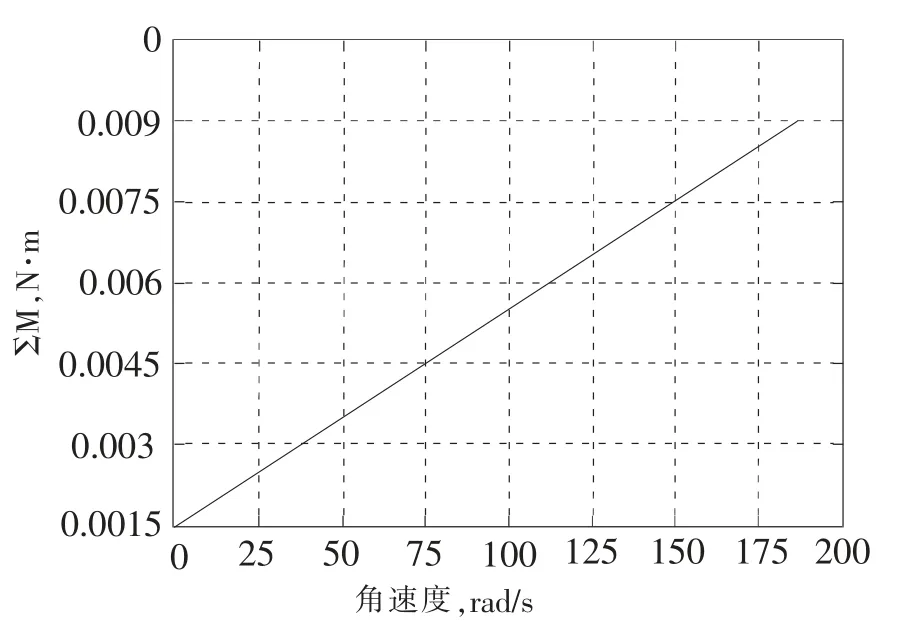
图6 轴颈处产生的弯矩

b——右平衡重距轴颈中心的距离

在UG 中分析得出 a=0.0457m，b=0.0404 m。将参数带入公式（2）中，在MATLAB 中计算得出ΣM 与曲轴旋转角速度的关系如图6。

1.2 现有气动马达静力学分析

曲轴在高速旋转过程中要承受很大的离心力做用，在符合动平衡原理的同时还要分析曲轴上应力的分布情况。 应避免局部应力集中[8]。 5×135 气动马达轴颈处受力最大，受其形状和所处位置的影响，轴颈根部成为最易变形和断裂的部位。 5×135 气动马达的最大旋转角速度为190 rad/s。在ansysworkbench14.5 中进行静力学分析，得出应力分布图如图7。

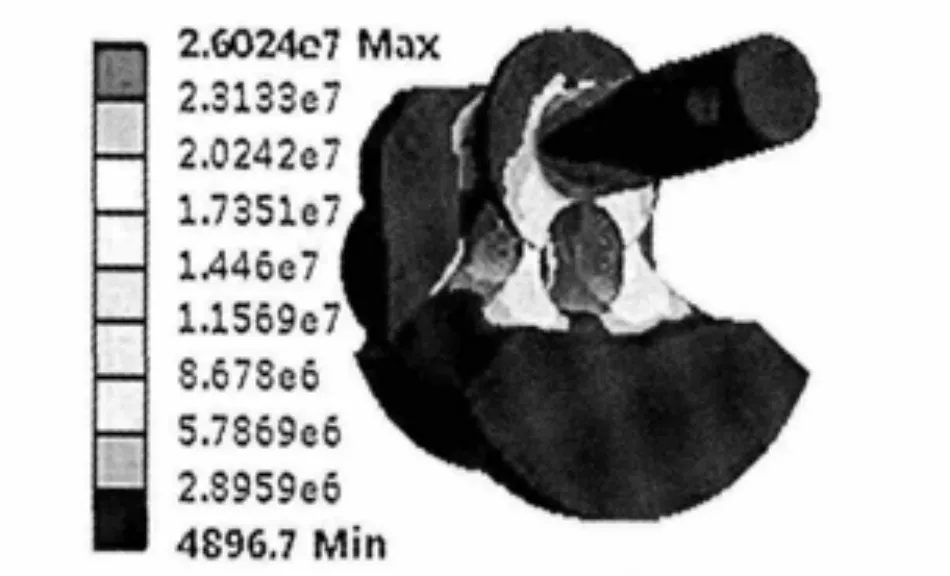
图7 未改进曲轴应力分布云图

2 曲轴的改进

通过分析图3 可知，现有气动马达曲轴的平衡重质量过小，造成气动马达在工作过程中产生了2800 N 的不平衡惯性力， 这些惯性力的生成是马达工作时振动和噪声产生的根本原因。在设计中应尽量避免产生这些惯性力[9]。因此，在保证曲轴轴颈弯矩不变大的前提下对目前使用马达的平衡重进行加重处理。在不干涉曲轴做旋转运动的条件下将平衡重半径由87 mm 增加到90 mm，将平衡重厚度由48 mm 减为47 mm。 这样可达到增加平衡重惯性力又不使其过量增重的效果[10]。 同时由于改为油雾润滑，将甩油盘去掉，曲轴外形也进行一定改进。 改后结构如图8。

图8 改进后曲轴结构

对改进后的曲轴产生的惯性力用公式 （1）进行计算，在UG 中对改进后的结构进行分析得出：m1=4.142kg，m2=3.883kg，c=0.0465m，d=0.046m。在MATLAB 中计算得出曲轴旋转角速度与不平衡惯性力的关系如图9。

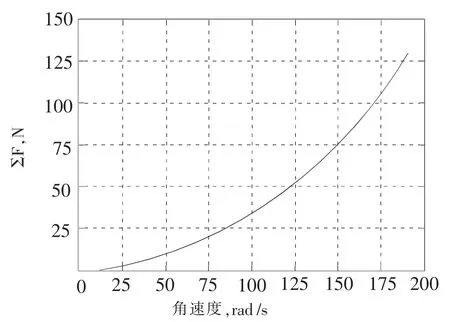
图9 改进后惯性力与角速度关系

对改进后曲轴轴颈上产生的弯矩用公式（2）进行计算， 改进后 a=0.043 m，b=0.047 m。 在MATLAB 中计算得到作用于曲轴的弯矩与曲轴旋转角速度关系如图10。 通过图5、6 与图9、10进行对比会发现，曲轴改进后未被平衡掉的惯性力为140 N， 现有结构未被平衡掉的惯性力为2800 N。改进后的弯矩为3.6×10-3N·m，现有结构弯矩为8.5×10-3N·m。 经过平衡重的改进明显减小了惯性力和弯矩。

同样转速下对改进后结构在Workbench 中进行静力学分析，得出应力云图如图11。 通过图7 与图11 的对比得出， 改进前轴颈根部产生最大应力为 1.73×107Pa， 改进后最大应力变为1.119×107Pa。

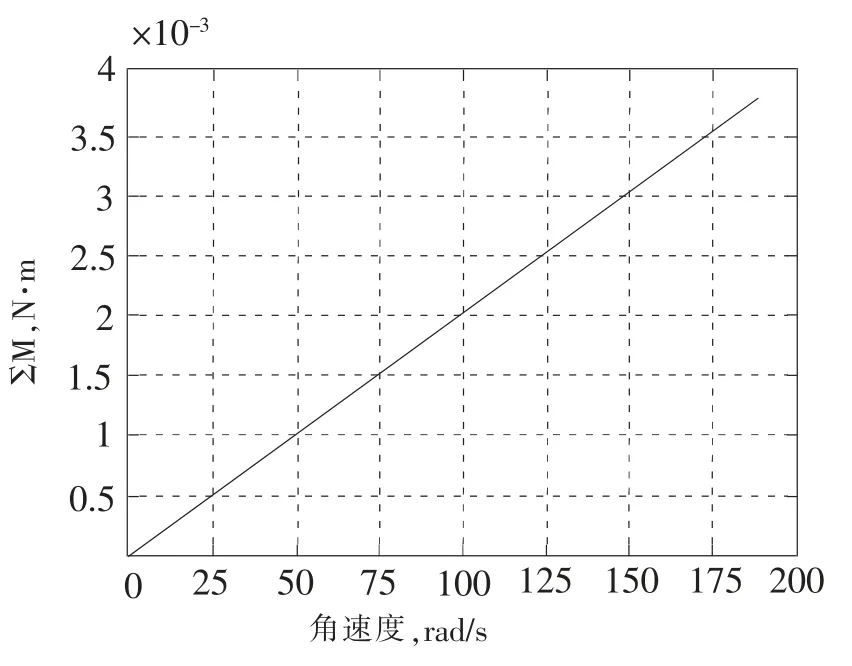
图10 改进后产生的弯矩

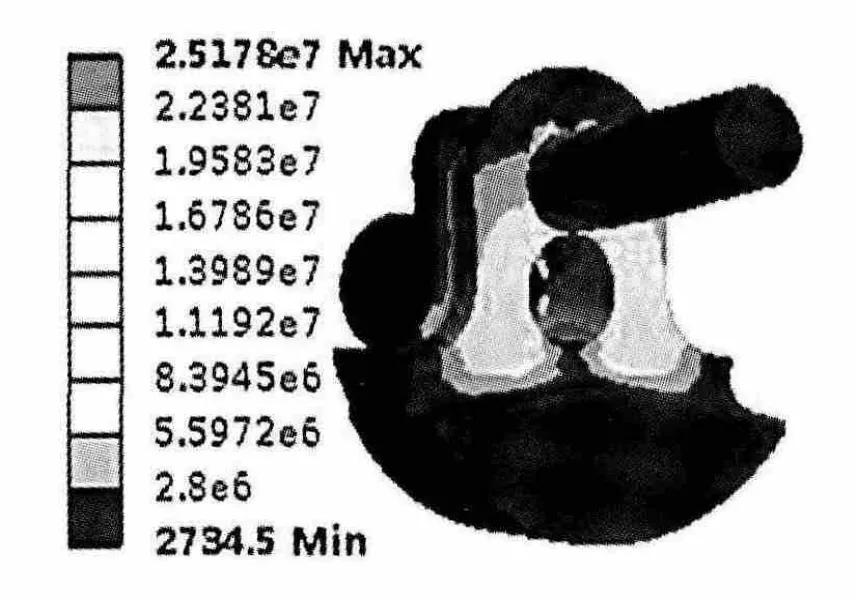
图11 改进后应力分布云图

3 结论

通过分析对比发现，改进后的曲轴运动时产生的不平衡力相对于改进前减小了2660 N，在轴颈处产生的弯矩相对于改进前减小了4.9×10-3N·m。 在轴颈根部最易变形处产生的最大应力相对于改进前减小了0.611×107Pa。 曲轴整体质量增加了0.014 kg。 达到了在满足动平衡要求的前提下少增加质量，并减小轴颈处的应力集中的要求。 通过对图9 的分析可以看出，将平衡重的质量设计的比刚好平衡时大0.05 kg，因为使用动平衡机进行测试时，对平衡重进行去重会比增加重量容易得多。 这种改进措施十分有效，达到了使马达平稳工作的目的。

[1]王秋晓，徐宗俊.单缸发动机平衡测试调整方法与实验的研究[J].中国机械工程，2006，(2)：131-134.

[2]程涛涛.用于汽车发动机曲轴的全自动动平衡修正系统的研究[D].浙江大学，2014.

[3]吴楠，廖日东，张保成.柴油机曲柄连杆机构多体动力学仿真分析[J].内燃机工程，2005，26(5)：69-73.

[4]袁兆成.内燃机设计[M].北京：机械工业出版社，2012.

[5]王明武，郁其祥，嵇绍岭.对少气缸发动机曲轴平衡特性的分析比较[J].内燃机工程，2001，22(3)：24-27.

[6]张保成，赵俊生，樊文欣.60°V8 发动机平衡分析及平衡机构设计[J].内燃机工程，2002，23(2)：20-23.

[7]董丹丹，覃文洁，刘金祥.直列六缸发动机曲轴两种平衡方案的分析比较[J].内燃机工程，2006，27(2)：39-42.

[8]陈致水，张燕，李粤.农用柴油机曲轴的有限元分析[J].农机化研究，2012，(1)：226-229.

[9]朱俊鹏，杜群贵，薛运锋.内摆线内燃机的动平衡研究[J].机械设计与制造，2009，(12)：99-101.

[10]彭禹，郝志勇.曲轴平衡重动态优化设计方法研究[J].农机化研究，2007，(03)：56-60.