基于高速高性能研磨机的研磨盘磨损仿真研究
付红栓,张永红,杨洪波,谯正武,李明娜,涂文静
(甘肃蓝科石化高新装备股份有限公司,甘肃 兰州730070)
0 引言
行星式双面研磨是精密加工中重要方法之一,在制造业中占有非常重要的地位。 但是随着一些脆硬材料的加工精度以及生产需求的提高,传统的行星式双面研磨加工已经不能满足生产要求。 为此德国柏林大学联合瑞士机床制造商Stahli, 根据行星式双面研磨加工原理成功研制了高速高性能研磨机,该研磨机能够打破传统研磨加工的束缚, 使研磨盘压力达到4000 N 以及研磨盘转速达到2000 r/min。 德国学者Uhlmann等运用该研磨机进行试验表明:切削速度的提高非但没有明显影响到工件的加工精度,而且可以增加工件的材料去除率,降低研磨盘磨损[1,2]。
在加工工程陶瓷等脆硬材料时研磨盘将会很快发生磨损,造成加工表面质量和精度严重下降,这就势必要频繁地修整研磨盘,不但影响加工效率,增加加工成本,也导致产品合格率降低。因此,对研磨盘磨损的研究就显得尤为重要。 研磨盘磨损主要从两个方面研究:一是研磨盘的磨损程度,研磨盘磨损越大,研磨盘使用寿命越短,对于生产者来说当然是磨损越小越好;二是研磨盘磨损的均匀性, 均匀性好能保证在批量加工中,在较长时间内加工的工件都具有较好的面形精度,从而降低研磨盘的修整频率,提高加工效率和产品合格率,并降低成本[3]。如果能在研磨机设计之初就预知研磨盘磨损情况,通过对研磨机结构以及研磨参数的优化,可降低研磨盘磨损并实现均匀磨损。
本文基于新研究出的高速高性能研磨机对研磨盘与工件的加工关系进行深入研究,首先通过求出过程运动轨迹,得到了研磨盘切削速度对研磨盘磨损程度的影响。然后通过求出研磨盘子圆环区域覆盖面积分布,来表征研磨盘不同区域的磨损量,确定研磨盘磨损形态。
1 高速高性能研磨机运动轨迹
研磨轨迹可分为两类:研磨盘上一定点相对于工件的运动轨迹为S1;工件上一定点相对于研磨盘的运动轨迹为S2。 S1直接关联着工件被加工表面的形貌特征、纹理分布,对于提高工件的加工精度具有重要意义[5],S2能直观的反映工件对研磨盘的影响,便于研磨盘磨损预测,本文主要对轨迹S2进行研究。
根据高速高性能研磨机的几何和运动参数,如图1 所示,通过求出任一时刻工件上P 点在研磨盘坐标系中的坐标,可建立运动轨迹方程:

式中,aZ为研磨盘中心到行星轮中心的距离,根据几何关系得aZ=(ra-ri)/2;eH为工件上P点到行星轮中心的距离。
引入加工时间tp,得到过程运动轨迹:


图1 几何和运动参数
2 研磨盘磨损仿真模型
所谓的研磨盘磨损仿真模型主要指将工件进行网格划分,并分别计算网格单元相对研磨盘划出的轨迹,进一步算出径向方向各个区间的网格单元的运动面积,以表征研磨盘不同区域的磨损情况。
2.1 研磨过程参数的引入
研磨盘磨损仿真模型的建立不仅需要行星式研磨运动的几何和运动参数,更需要材料去除率Zw、研磨工件深度△h 和加工时间tp等加工过程参数,这样才能更真实、全面地对研磨盘的磨损进行预测仿真。
将每次加工过程中的工件研磨深度△h 设为定值,用其除以研磨的材料去除率Zw,可以得到过程加工时间tp[2]:

式中,Zw通过大量试验获得。 材料去除率Zw与研磨盘硬度、切削速度、压力和磨粒粒度等工艺参数有关[6],因此Zw的使用是间接地考虑了这些过程工艺参数的影响, 使该仿真更能接近实际。 在切削速度vc=5 m/s 时实验获得材料去除率Zw=5 μm/s;vc=25 m/s 时实验获得材料去除率 Zw=51 μm/s, 可以看出切削速度的提高可以明显地增加材料去除率[1]。
2.2 研磨盘子圆环区域的覆盖面积分布
根据Preston 方程[7],整理得到第i 个子圆环在覆盖面积为Sei时的研磨盘磨损量:

式中 k——与被加工材料、 工艺参数等有关的系数
p——研磨压力
d——网格单元边长
Ri——第i 个子圆环区域的磨损量
将系数k、研磨压力p 设为定值,网格单元边长d 为决定dS 的定值。 于是得:

由式(8)可以看出,研磨盘磨损与系数k、研磨压力 p、子圆环覆盖面积 Sei成正比。 在 k、p 为定值时,可用Sei来表征第i 个子圆环的磨损量。
鉴于一个工件足以用来分析研磨盘的磨损情况,故只需要研究一个工件对研磨盘的影响即可。为了研究研磨盘不同区域的磨损情况将研磨盘划分成k 个呈同心圆排列的子圆环区域,为了研究工件整个接触表面对研磨盘的影响将工件进行网格划分,如图2 所示。
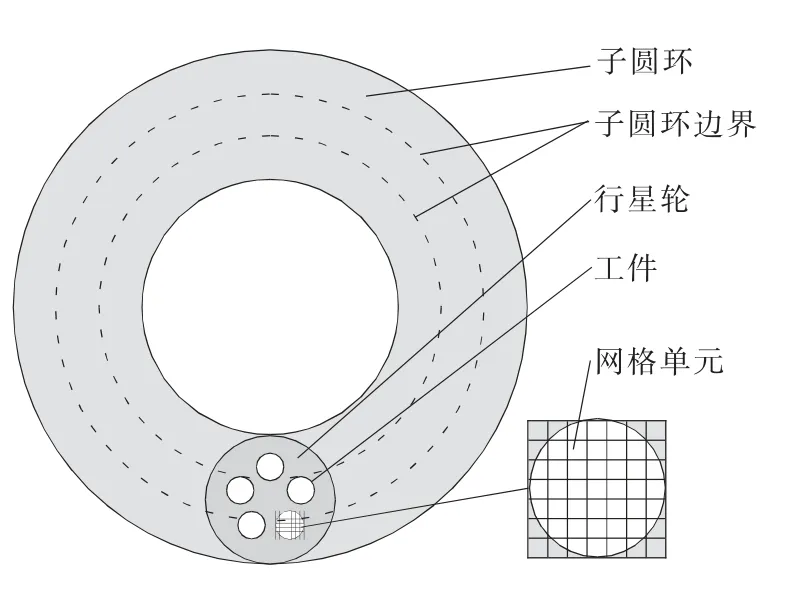
图2 子圆环区域与网格单元
拿出一个网格单元进行分析,将该网格单元简化为一点,在加工时间tp内,计算其在第i 个子圆环内的轨迹覆盖长度lei。 由于运动轨迹会横跨不同的子圆环,故在分析网格单元的局部运动时,可分为两种情况,如图3 所示。
情况一,网格单元先后运动的两点在同一子圆环内时,可直接计算这两点的距离,则该网格单元的运动轨迹在第i 个圆环覆盖长度为:

图3 网格单元的局部运动
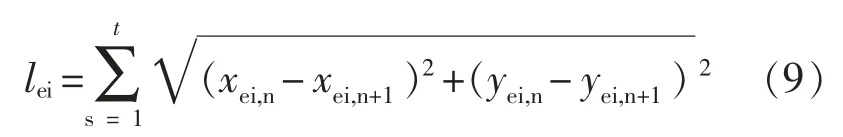
情况二, 网格单元先后运动的两点在不同的两个子圆环内时,此时需要先计算第一点(xei,m,yei,m)到下一个子圆环边界交点(xeij,yeij)的距离,然后再计算边界交点到第二点(xei,m+1,yei,m+1)的距离,则该网格单元的运动轨迹在第i 个圆环和第j 个圆环的覆盖长度分别为:

研磨盘上第i 个子圆环区域的轨迹覆盖长度是工件上所有网格单元在该子圆环上反复运动求和的长度。对所有子圆环区域的轨迹覆盖长度进行计算,可得研磨盘上不同子圆环区域的轨迹覆盖分布

第i 个子圆环区域的轨迹覆盖长度lei与网格单元的边长d 的乘积即为第i 个子圆环区域的覆盖面积Sei,所有子圆环区域的覆盖面积组成覆盖面积分布为

不同子圆环区域有相同的覆盖面积时,研磨盘量相同。但实际情况是有相同覆盖面积的子圆环区域,子圆环区域面积越小,研磨盘磨损越剧烈,即研磨盘磨损程度不能简单的用子圆环区域覆盖面积表征。为此需要引入相对子圆环区域覆盖面积的概念,用来表示不同子圆环区域的磨损程度。相对子圆环区域覆盖面积即指子圆环区域覆盖面积相对子圆环区域面积的大小,可用子圆环区域覆盖面积除以子圆环区域面积计算得到。
3 仿真实验与结果
3.1 仿真实验
使用型号为D91C75 的树脂结合剂金刚石研磨盘对Al2O3工程陶瓷进行研磨, 利用Matlab对研磨过程仿真。根据实际使用的试验材料和参数,分别给出研磨加工的几何参数取值和研磨加工过程中的工艺参数取值,如表1 所示。

表1 仿真参数取值
通过对研磨盘转速nu和内齿圈转速ni这两个参量的调节可改变切削速度vc,因此通过已知的切削速度结合公式(3)可以计算得到研磨盘转速 nu和内齿圈转速 ni, 将 nu、ni、ri和 ra等参数带入公式(5),得到过程运动轨迹,如图 4 所示。 结合仿真参数取值将(4)式应用到(9)~(13)式,得到研磨盘子圆环区域覆盖面积分布, 如图5 所示。 根据相对子圆环区域覆盖面积的概念,得到相对子圆环区域覆盖面积分布,如图6 所示。
3.2 仿真结果与分析
图4 为vc=5 m/s 和vc=25 m/s 时的过程运动轨迹,由图可以明显看出,切削速度的提高可以明显缩短工件在研磨盘上的运动轨迹长度, 这主要是因为伴随着切削速度提高,材料去除率增大,加工时间减少。 工件上一点相当于“磨粒点”对研磨盘进行反“切削”,轨迹长度越短表明研磨盘的磨损越小, 由此看出切削速度的提高可以使研磨盘的磨损程度降低,这与实验验证基本一致。

图4 过程运动轨迹

图5 子圆环区域覆盖面积分布
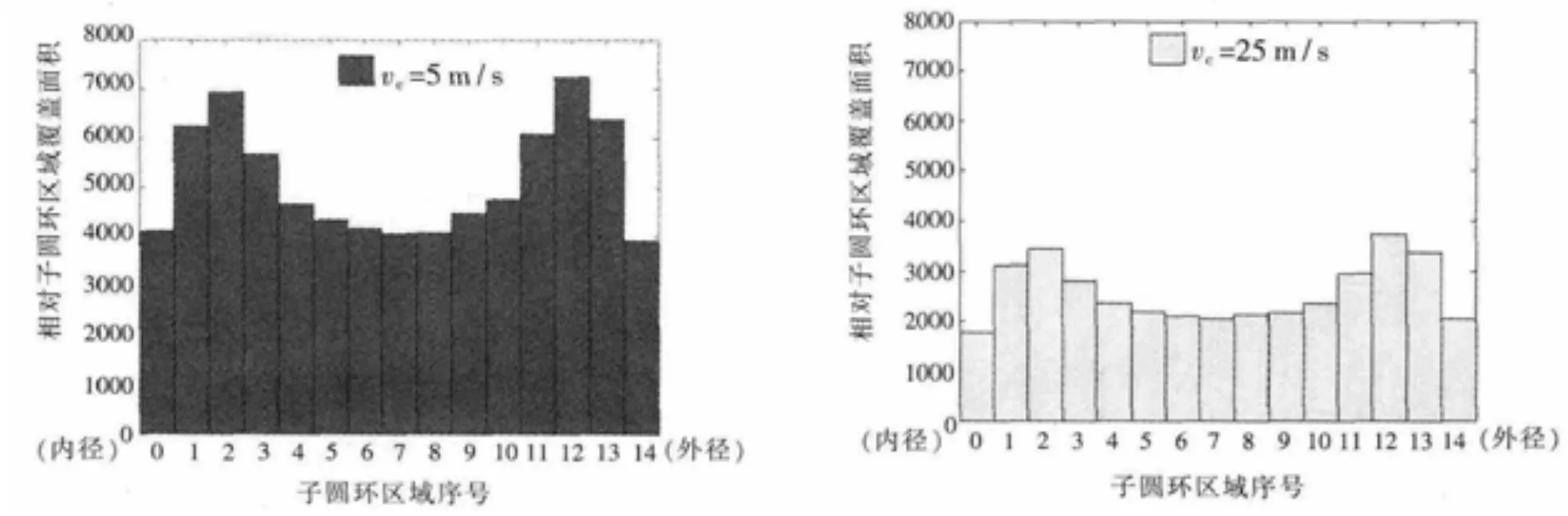
图6 相对子圆环区域覆盖面积分布
由图5 知,两种切削速度下子圆环区域的覆盖面积分布特征基本相同,均在研磨盘靠近内外径的区域有较大覆盖面积,且靠近外径的子圆环平均覆盖面积要大于靠近内径的子圆环平均覆盖面积;同时也可以看出,切削速度提高,子圆环区域覆盖面积整体减少, 这是因为切削速度提高,缩短了运动轨迹长度。
由图6 知,研磨盘靠近内外径区域的相对子圆环区域覆盖面积较大,且研磨盘上相对子圆环区域覆盖面积分布基本对称; 同样切削速度提高,相对子圆环区域覆盖面积也整体减少。
由上结果可知,切削速度的提高可以使研磨盘的磨损降低,靠近研磨盘内外径的区域的磨损明显大于中径区域,且研磨盘径向方向的磨损基本对称。 研磨盘磨损不均匀会改变研磨盘平整度, 不平整的研磨盘会造成研磨压力不均匀,导致工件平面度达不到加工要求。在实际生产中一般采用修盘器对研磨盘进行修整来保证研磨盘的平面度。 在预知磨损形态的情况下,通过对研磨参数和研磨机结构的优化, 使研磨盘磨损均匀,以保证研磨盘的平面度。
4 结论
(1)分析了新研究出的高速高性能研磨机的运动原理。 建立了研磨盘磨损仿真模型,该模型通过求出研磨盘子圆环区域覆盖面积分布,预测了研磨盘径向不同区间的磨损情况。
(2)根据仿真结果知,切削速度的提高缩短了运动轨迹长度,研磨盘磨损减小;切削速度一定时,研磨盘靠近内外径区域磨损程度明显高于中径区域,且研磨盘径向方向的磨损基本对称。
(3)本文研磨盘磨损的预测仿真方法也可应用到其它类型的研磨机上,在研磨机设计之初就能预知研磨盘的磨损形态,并对研磨机进一步结构优化,以保证研磨盘平面度,从而可以降低研磨盘的修整频率, 提高加工效率和产品合格率,并降低成本。
[1]Uhlmann E,Hoghé T.Wear reduction at double face grinding with planetary kinematics [J].Prod Eng Res Devel,2012,6(3):237~242.
[2]Uhlmann E, Hoghé T, Kleinschnitker M.Grinding wheel wear prediction at double face grinding with planetary kinematics using analytic simulation [J].Int J Adv Manuf Technol,2013,69(9-12):2315~2321.
[3]杨鑫宏,胡忠辉,张伟,等.平面研磨中基于磨具均匀磨损的磨具设计方法研究 [J]. 机械工程学报,2004,40(11):183~187.
[4]吴宏基,曹利新,刘健.基于行星式平面研磨机研抛过程的运动几何学分析 [J]. 机械工程学报,2002,6(6):144~147.
[5]盛继生,文东辉,计时鸣.主动驱动条件下研磨轨迹均匀性的研究[J].农业机械学报,2010,41(4):209~212,221.
[6]胡海明,李淑娟,高晓春等.SiC 单晶片研磨过程材料去除率仿真与试验研究 [J]. 兵工学报,2013,34(9):1125~1131.
[7]张红霞,高宏刚,吴明根.定偏心锡磨盘超精密平面抛光均匀去除模拟计算(I)[J].光学精密工程,1998,6(2):77~82.

