机床支撑地脚结合部法向粗糙接触建模

田红亮，余 媛，张 屹

（三峡大学 机械与动力学院，湖北 宜昌443002）

将式（39）代入式（42）得［12］

机床整机动态特性是指机床整机结构在动态力作用下所展现出来的动态特性，通常包含振型、固有频率、阻尼比、谐响应、动刚度、动柔度等［1］.国内早在从20世纪80年代初期开始，北京机床研究所与陕西机械学院开展对整机动态特性的研发，编制了“金属切削机床样机试验规范总则（试行稿）”，并开发了机床整机结构参数优化分析软件包［2］.Greenwood等［3］率先研究了粗糙表面的微观接触机理，架构了粗糙表面的弹性接触理论，即GW 理论.Polycarpou等［4］对GW 理论中简单的指数分布进行了修正，采用修正的指数分布推导出了接触粗糙表面法向接触参数的解析近似解.Chang等［5］考虑微接触点的2种变形方式，纯弹性和塑性，根据两半球体微接触点在塑性变形时球台体积守恒建立接触粗糙表面实际接触面积和法向接触负载的分析解，但该模型只考虑了微凸体的完全弹性变形与完全塑性变形机制，没计及两者之间的弹塑性过渡变形机制，因此在临界屈服点处导致法向接触载荷不连续.Tian等［6-9］联合分形理论和等效虚拟材料的有限元建模思路分析了螺栓结合部的接触特性.尤晋闽等［10］基于对粗糙表面形貌统计分析的基础上，综合考虑微凸体的完全弹性、弹塑性与完全塑性3种变形机制，构建了结合部的接触面积、接触载荷与接触刚度的统计模型.Zhao等［11］按照微凸体变形的连续性以及光滑性，用模板3次多项式拟合了弹塑性变形阶段，提出了一种结合部弹塑性接触模型，但对于弹塑性变形区间接触压应力的估计不够准确.机床的安装通常需要在床身与地基之间放置可以调整机床水平的支撑地脚，但现有文献在对机床整机动态特性进行分析时，大多忽略了地脚的影响.近年来随着机床向高速化发展，在高速切削领域机床的动态特性对机床性能的影响更加显著.随着有限元理论、分析软件、机床振动测量与分析仪器的发展，当前国内外又一次开展了机床动态特性研究热潮.

综上所述，现有的微观接触力学理论还未对地脚进行全面的研究，本文在以上研究的基础上，以混凝土地坪与标准平板互相接触形成的金属切削机床底座支撑地脚结合部为考察对象，考虑微接触点的2个弹塑性变形区域，构架干摩擦金属结合部法向接触参数的统计模型.

1 地脚结合部的微观变形与宏观参数

机床底座支撑地脚结合部的组成见图1.

混凝土地坪与标准平板的微观接触见图2，其中，z为混凝土地坪微接触点的高度，d 为混凝土地坪与标准平板之间的间距，w 为微接触点的法向变形量，R 为微接触点的半径.

微接触点的法向变形量为

微接触点的弹性临界法向变形量［5］为

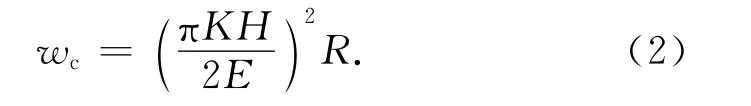
式中：K 为最大接触压应力因子，K ＝0.454＋0.41ν，ν为较软材料的泊松比；H 为较软材料的硬度；E 为当量弹性模量，表达式为

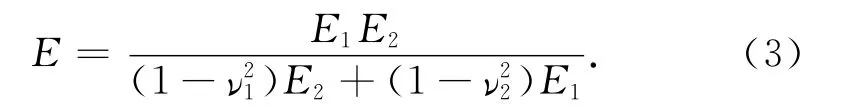
式中：E1与ν1分别为混凝土地坪的弹性模量与泊松比；E2及ν2依次为标准平板的弹性模量及泊松比.

Kogut等［12］认为，当wc≤w ≤110wc，微接触点处于弹塑性变形范围.根据数值计算结果，整个弹塑性阶段又分为弹塑性变形Ⅰ区（wc≤w ≤6wc）和弹塑性变形Ⅱ区（6wc≤w ≤110wc）.

1.1 微接触点的弹性变形

当w ＜wc时，微接触点发生弹性变形.单个微接触点的弹性接触面积为

整个结合部的实际弹性接触面积为

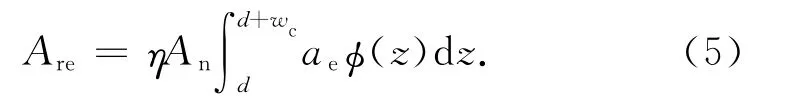
式中：η为微接触点的面密度；An为名义接触面积；φ（z）为微接触点高度分布的概率密度.

将式（4）代入式（5）得

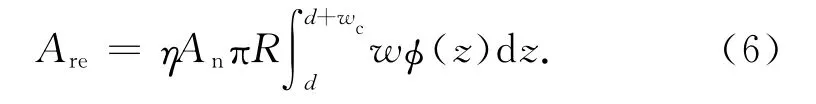
将式（1）代入式（6）得

式中：σ为微接触点高度分布的标准差.

式（8）可变为［13］

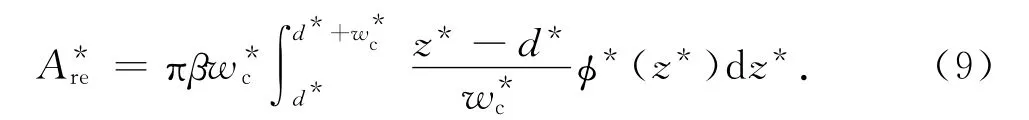
式中：β ＝ηRσ 为表面粗糙度参量；z＊＝z／σ；d＊＝d／σ；w＊c＝wc／σ；φ＊（z＊）＝σφ（σz＊）；φ（z）dz＝φ＊（z＊）dz＊.

单个微接触点的弹性接触负载为

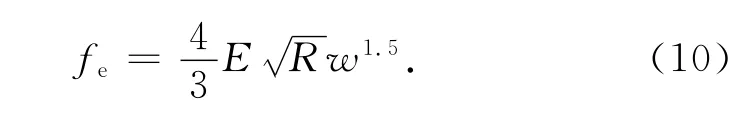
整个结合部的弹性接触负载为

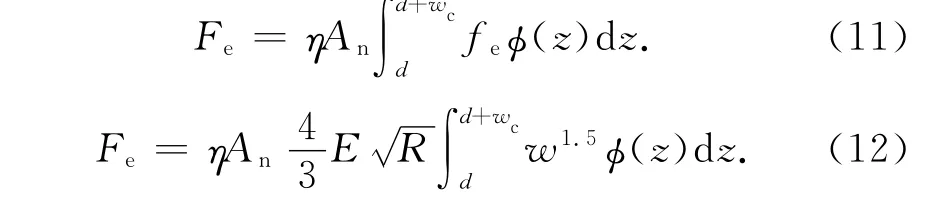
将式（1）代入式（12）得

将式（17）代入式（15）得［13］

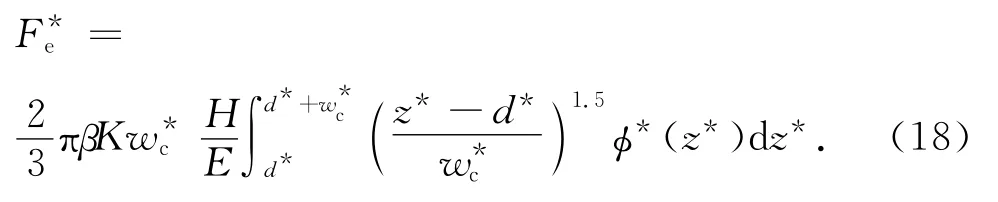
由式（10）可得微接触点与标准平板的弹性接触刚度为

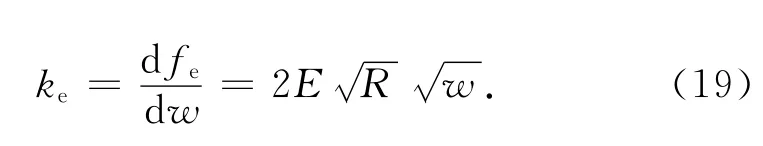
若w ＜wc时，由弹性接触刚度引起的弹性应变能为

整个结合部的弹性接触刚度为

将式（19）代入式（21）得

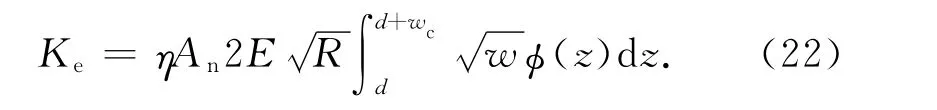
将式（1）代入式（22）得

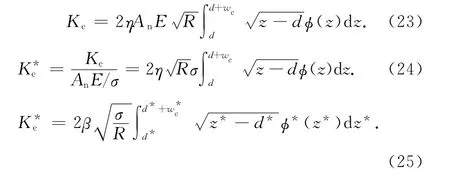
1.2 微接触点的弹塑性变形

当w ＝wc时弹性临界接触 面积ac满足［12］

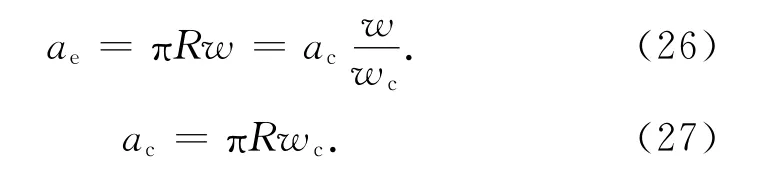
第Ⅰ弹塑性接触面积aep1满足［12］

整个结合部的第Ⅰ实际弹塑性接触面积为

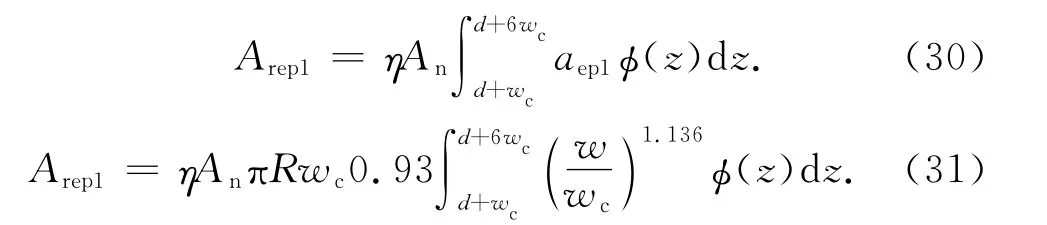
将式（1）代入式（31）得

量纲为1的第Ⅰ实际弹塑性接触面积为

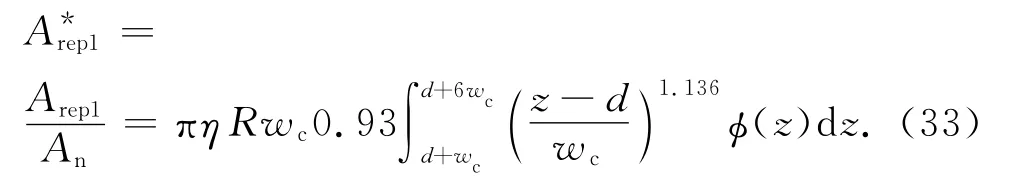
式（33）可变为［13］

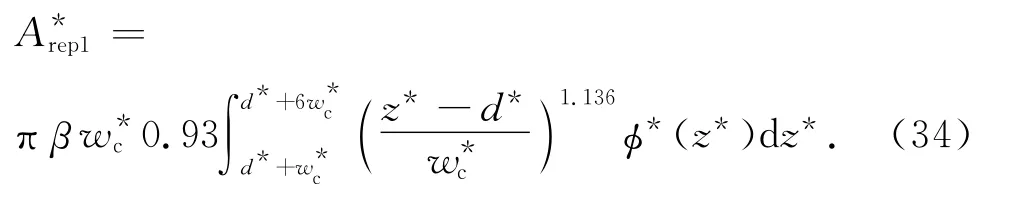
当w ＝wc时，弹性临界接触负载fc满足［12］

当w ＝wc时，平均接触压应力为

将式（27）和（36）代入式（37）得

将式（2）代入式（38）得［12］

平均弹性接触压应力［12］为

将式（26）和（35）代入式（40）得

将式（37）代入式（41）得［12］

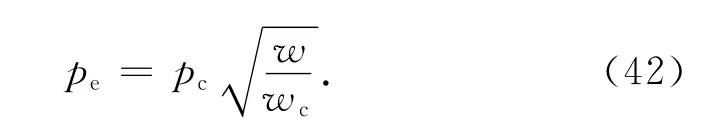
将式（39）代入式（42）得［12］

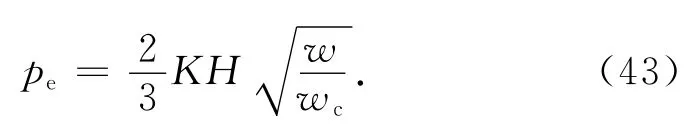
将式（43）代入式（41）得

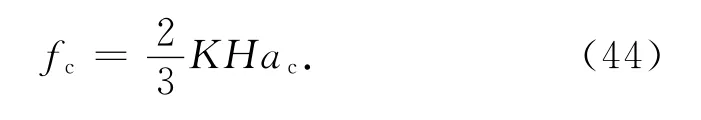
将式（27）代入式（44）得

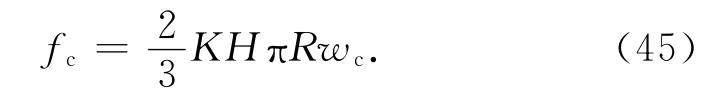
第Ⅰ弹塑性接触负载fep1满足［12］

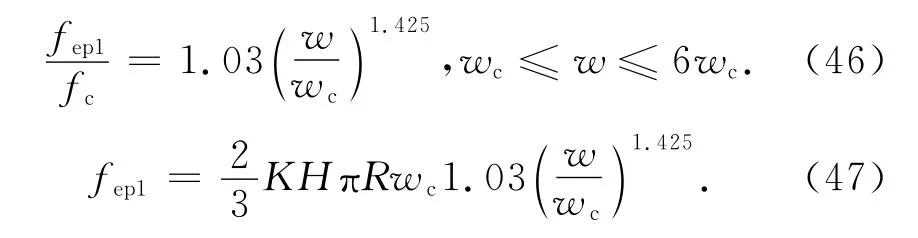
整个结合部的第Ⅰ弹塑性接触负载为

将式（1）代入式（49）得

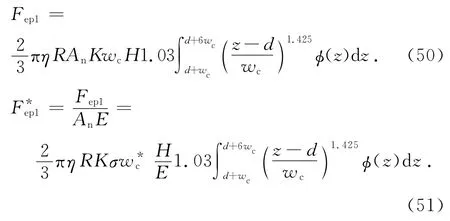
式（51）可变为［13］

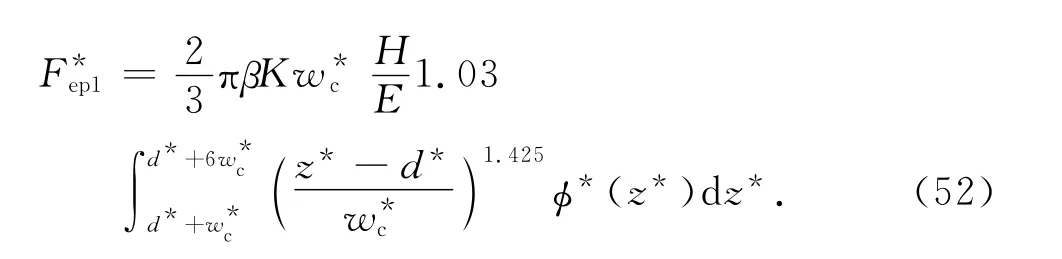
发生弹塑性的微接触点产生弹塑性应变能.没有达到弹性极限的微接触点对弹性应变能有贡献，根据式（20）可得区域Ⅰ的弹性应变能为

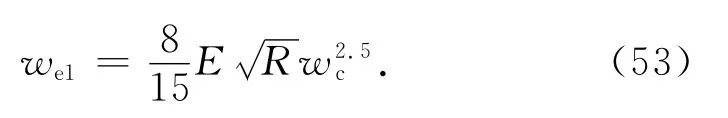
按照式（19），弹性接触刚度随着w 的增加而增加，直到w ＝wc时达到最大值为止，因此第Ⅰ弹塑性接触刚度为

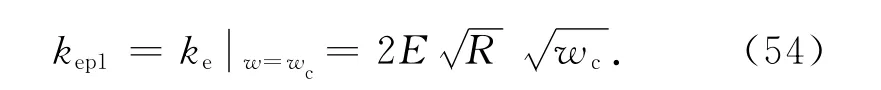
整个结合部的第Ⅰ弹塑性接触刚度为

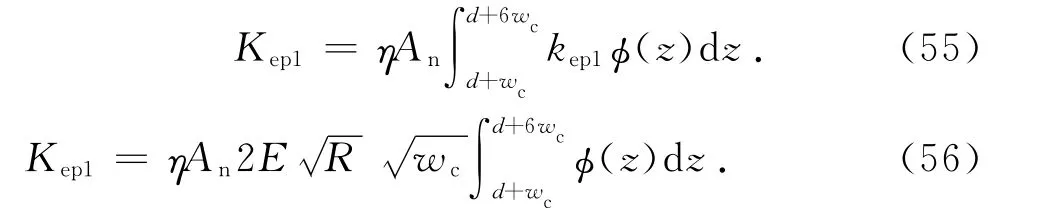
量纲为1的第Ⅰ弹塑性接触刚度为

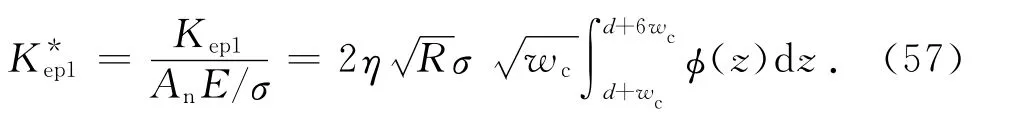
式（57）可变为

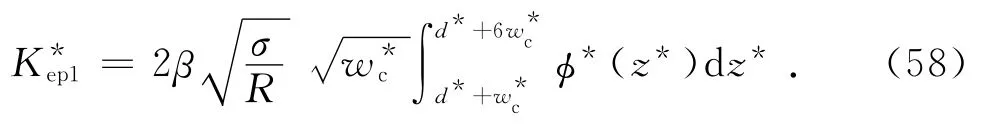
第Ⅱ弹塑性接触面积aep2满足［12］

将式（27）代入式（59）得

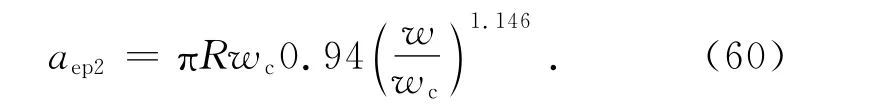
整个结合部的第Ⅱ实际弹塑性接触面积为

将式（1）代入式（62）得

式（64）可变为［13］

第Ⅱ弹塑性接触负载fep2满足［12］

将式（45）代入式（66）得

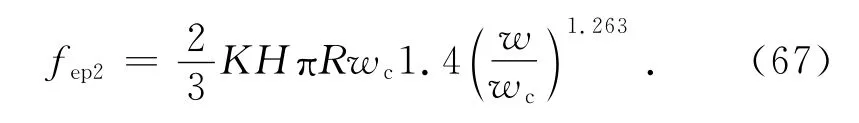
整个结合部的第Ⅱ弹塑性接触负载为

将式（1）代入式（69）得

式（71）可变为［13］

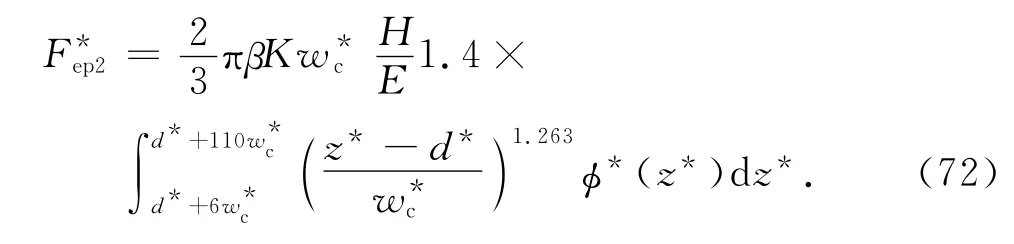
第Ⅱ弹塑性接触刚度为

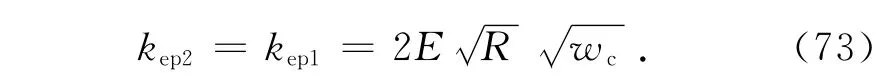
整个结合部的第Ⅱ弹塑性接触刚度为

量纲为1的第Ⅱ弹塑性接触刚度为

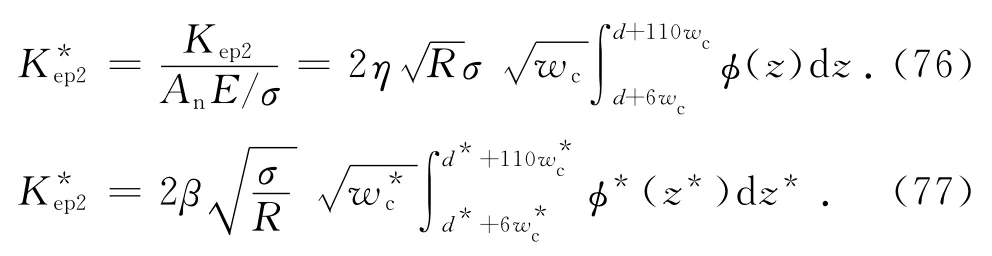
1.3 微接触点的塑性变形

当w ＞110wc时，微接触点发生塑性流动.单个微接触点的塑性接触面积［10］为

整个结合部的实际塑性接触面积为

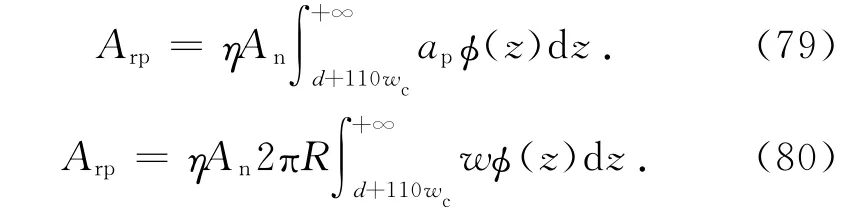
将式（1）代入式（80）得

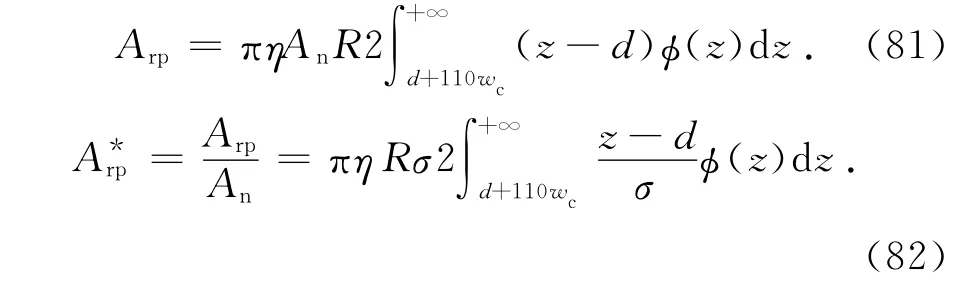
式（82）可变为［13］

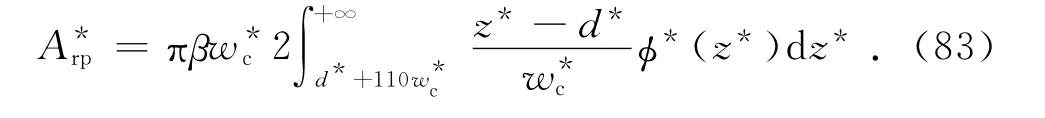
单个微接触点的塑性接触负载［10］为

整个结合部的塑性接触负载为

将式（1）代入式（86）得

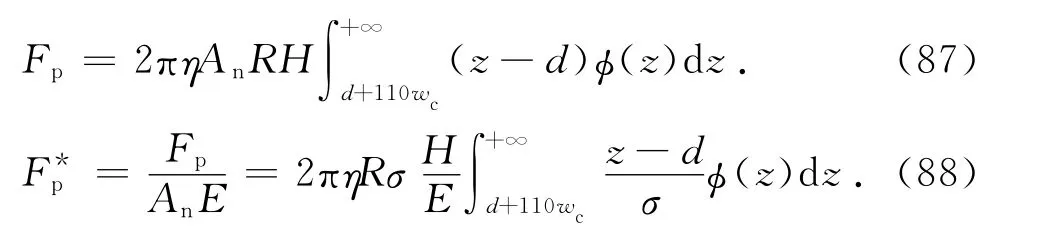
式（88）可变为［13］

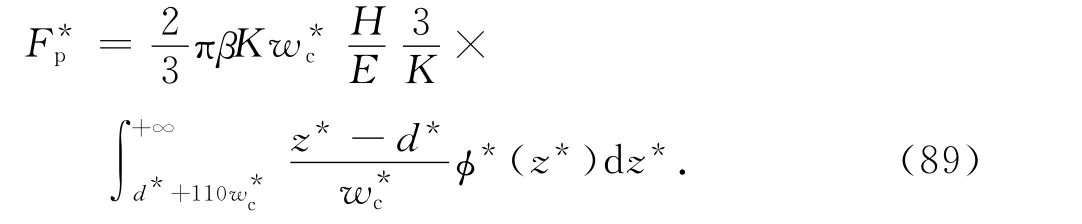
塑性接触刚度为

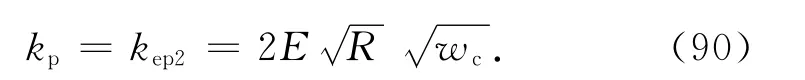
整个结合部的塑性接触刚度为

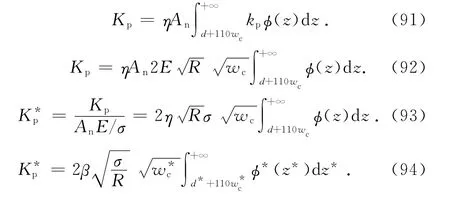
1.4 整个结合部的法向接触参数

量纲为1的实际接触面积为

将式（9）、（34）、（65）、（83）代入式（95）得［13］

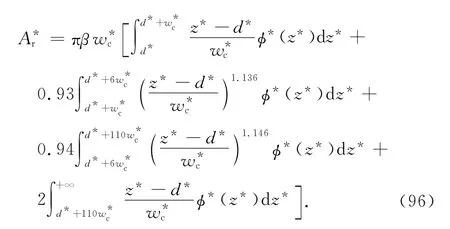
量纲为1的法向接触负载为

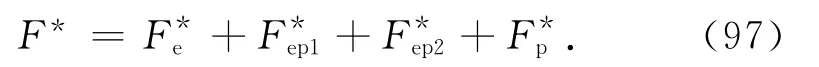
将式（18）、（52）、（72）、（89）代入式（97）得［13］

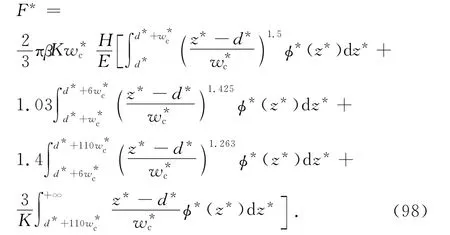
量纲为1的法向接触刚度为

将式（25）、（58）、（77）、（94）代入式（99）得

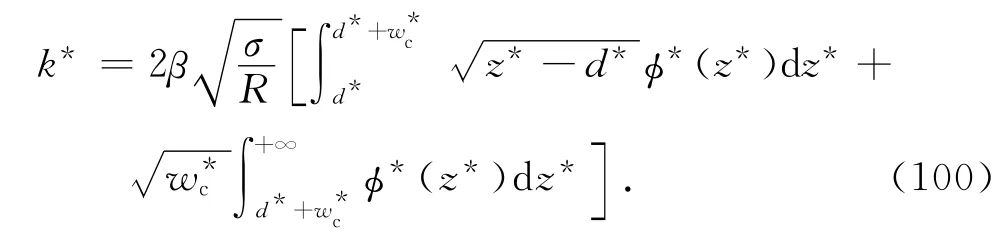
金属制品塑性指数为

将式（16）代入式（101）得

2 地脚结合部加载的仿真

金属地脚结合部材料采用同种材料普通碳素结构钢Q235，参数为：E1＝E2＝2.07×1011Pa，H ＝1.96×109Pa，ν1＝ν2＝0.29.表面微观几何学形貌参数和待求解的塑性指数见表1.

在表1中取塑性指数ψ＝1.113 4，如图3所示表示在微接触点高度的3种概率密度下实际接触面积、法向接触负载和法向接触刚度的比较情形.从图3中看出，地脚结合部的实际接触面积、法向接触负载与法向接触刚度都随着混凝土地坪与标准平板之间间距的降低而增加，主要是因为混凝土地坪与标准平板之间间距的减少引起出现接触的微接触点的数目增多，使得实际接触面积增加，为此需求更高的法向接触负载，更大的法向接触负载做功越多，地脚结合部间存储的弹性应变能越大，法向接触刚度上升.当间距较大时，GW 理论过高预测法向接触参数，当d＊＝4时，GW 理论比本文大5个数量级.除了在d＊＝0和d＊＝4两端附近区域外，在间距的正常范围内，本文预测的法向接触参数介乎GW 理论、文献［4］之间.

表1 涂层微观形貌参数和导出塑性指数Tab.1 Coating micro topographical parameters and deducible plasticity indices

图3 各种概率密度下法向接触参数Fig.3 Normal contact parameters for different probability densities

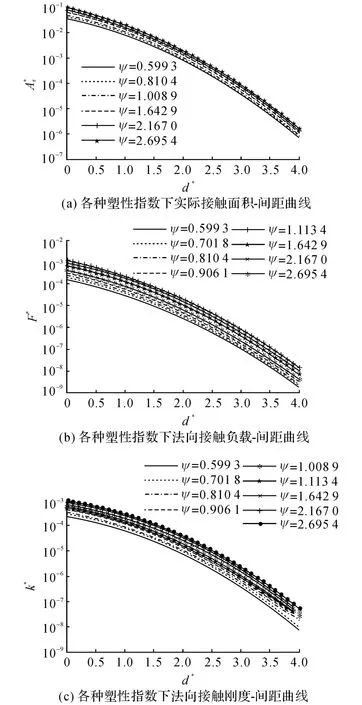
图4 各种塑性指数下的法向接触参数Fig.4 Normal contact parameters for diverse plasticity indexes

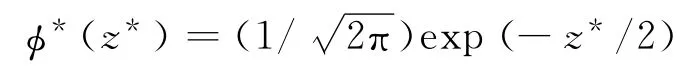
3 地脚结合部加载的试验验证

在有限元软件ANSYS Workbench 中建立床身地脚结合部动力学模型［14］，将本文利用解析方法得到的法向接触刚度嵌入到整体的有限元建模中.在对有限元模型进行模态分析的基础上，进一步对仿真模型进行谐响应分析.最后对测试试件试验、忽略地脚参数仿真、考虑地脚参数仿真3种模式下的频率响应函数进行对比［15］，见图5.f 为频率.由图5可知当考虑地脚结合部参数仿真值共振频率与共振峰值更符合试验值；忽略地脚结合部参数仿真值共振频率大于试验值，共振峰值小于试验值.

根据三阶模态试验频率、阻尼比和相关几何参数，可以解算x、y、z 这3 个方向的刚度和阻尼.本文法向接触刚度与试验结果的对比见图6，随着正压力的增大，本文法向接触刚度曲线和z 轴法向试验曲线走势一致.

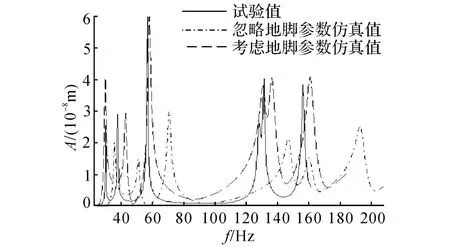
图5 各种模式下的频率响应函数Fig.5 Frequency response functions under distinct modes

4 结 论

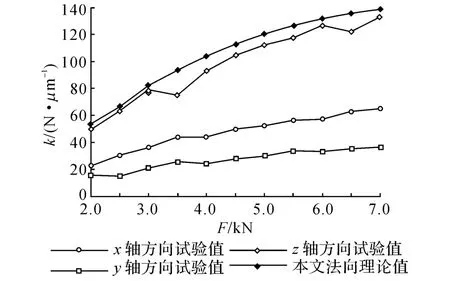
图6 理论法向接触刚度与试验的对照Fig.6 Comparison of theoretical normal contact stiffness with experimental one

（1）地脚结合部的实际接触面积、法向接触负载与法向接触刚度均随着混凝土地坪与标准平板之间间距的减少而增大.

（2）地脚结合部的实际接触面积、法向接触负载及法向接触刚度皆随着塑性指数的增大而变大.

（3）通过有限元仿真的比较能够看出，考虑了地脚参数的模型得到的谐响应分析和法向接触刚度结果与试验结果更为接近，间接和直接地验证了地脚结合部法向参数辨识的准确性.

（4）单对微接触点的法向接触刚度等于法向接触负载对微接触点法向变形量的一阶导函数.

（

）：

［1］叶佩青，王仁彻，赵彤，等.机床整机动态特性研究进展［J］.清华大学学报：自然科学版，2012，52（12）：1758-1763.YE Pei-qing，WANG Ren-che，ZHAO Tong，et al.Recent research advances of whole machine tool dynamics［J］.Journal of Tsinghua University：Science and Technology，2012，52（12）：1758-1763.

［2］黄玉美，付卫平，董立新，等.结合面法向动态特性参数研究［J］.机械工程学报，1993，29（3）：74-78.HUANG Yu-mei，FU Wei-ping，DONG Li-xin，et al.Research on the dynamic normal characteristic para meters of joint surface［J］.Chinese Journal of Mechanical Engineering，1993，29（3）：74-78.

［3］GREENWOOD J A，WILLIAMSON J B P.Contact of nominally flat surfaces［J］.Proceedings of the Royal Society of London：Series A Mathematical and Physical Sciences，1966，295（1442）：300-319.

［4］POLYCARPOU A A，ETSION I.Analytical approximations in modeling contacting rough surfaces ［J］.Transactions of the ASME Journal of Tribology，1999，121（2）：234-239.

［5］CHANG W R，ETSION I，BOGY D B.An elastic-plastic model for the contact of rough surfaces［J］.Transac-tions of the ASME Journal of Tribology，1987，109（2）：257-263.

［6］TIAN Hong-liang，LI Bin，LIU Hong-qi，et al.A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools［J］.Elsevier International Journal of Machine Tools ＆ Manufacture，2011，51（3）：239-249.

［7］田红亮，方子帆，朱大林.赫兹点接触133年［J］.三峡大学学报：自然科学版，2014，36（2）：88-97.TIAN Hong-liang，FANG Zi-fan，ZHU Da-lin.133years of Hertz point contact［J］.Journal of China Three Gorges University：Natural Sciences，2014，36（2）：88-97.

［8］左婧，徐卫亚，王环玲，等.岩石电镜扫描图像的分形特征研究［J］.三峡大学学报：自然科学版，2014，36（2）：72-76.ZUO Jing，XU Wei-ya，WANG Huan-ling，et al.Fractal analysis of SEM image for rocks［J］.Journal of China Three Gorges University：Natural Sciences，2014，36（2）：72-76.

［9］田红亮，郑金华，方子帆，等.阻尼系统的特征［J］.三峡大学学报：自然科学版，2015，37（2）：75-82.TIAN Hong-liang，ZHENG Jin-hua，FANG Zi-fan，et al.Characters of damping system［J］.Journal of China Three Gorges University：Natural Sciences，2015，37（2）：75-82.

［10］尤晋闽，陈天宁.结合面静态接触参数的统计模型研究［J］.振动与冲击，2010，29（11）：47-50，252.YOU Jin-min，CHEN Tian-ning.Statistical model for static contact parameters of joint surfaces［J］.Journal of Vibration and Shock，2010，29（11）：47-50，252.

［11］ZHAO Yong-wu，MAIETTA D M，CHANG L.An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow［J］.Transactions of the ASME Journal of Tribology，2000，122（1）：86-93.

［12］KOGUT L，ETSION I.Elastic-plastic contact analysis of a sphere and a rigid flat［J］.Transactions of the ASME Journal of Applied Mechanics，2002，69（5）：657-662.

［13］KOGUT L，ETSION I.A finite element based elasticplastic model for the contact of rough surfaces［J］.Tribology Transactions，2003，46（3）：383-390.

［14］张辉，于长亮，王仁彻，等.机床支撑地脚结合部参数辨识方法［J］.清华大学学报：自然科学版，2014，54（6）：815-821.ZHANG Hui，YU Chang-liang，WANG Ren-che，et al.Parameters identification method for machine tool support joints［J］.Journal of Tsinghua University：Science and Technology，2014，54（6）：815-821.

［15］温淑花，张宗阳，张学良，等.固定结合面刚度分形模型［J］.农业机械学报，2013，44（2）：255-260.WEN Shu-hua，ZHANG Zong-yang，ZHANG Xue-liang，et al.Stiffness fractal model for fixed joint interfaces［J］.Transactions of the Chinese Society for Agricultural Machinery，2013，44（2）：255-260.