基于功能单元的主动结构形状的仿生控制

杨鹏程，罗尧治，沈雁彬

（浙江大学 空间结构研究中心，浙江 杭州310058）

主动结构（active structures，AS）是一类同时包含被动（静态）构件与主动（动态）构件的结构［1］.AS的适用性控制是结构主动控制领域中重要研究目标之一［2-5］，自20世纪末以来，AS的形状控制成为了一项重要的研究课题［6-10］.

AS一般通过调节构件长度的方式进行形状的改变.为满足形状控制目标，一个主要问题就是如何求解主动构件的执行量.一些研究者针对小变形假定情况下的AS 线性控制进行研究［5，11-13］，而对于更为一般的情况来说，当AS几何非线性效应较为明显、主动构件数目较多、主动构件的可调范围较大时，求解执行量的整个搜索空间会相当大，以至于通过启发式选择或穷举算法的计算量过大，从而难以找到可行或接近优化的解.以随机搜索算法为主的AS形状控制方法成为了当前解决这一问题的主流研究路线［3，14-15］.Fest等［9，16］设计了主动结构的原型并提出了基于随机搜索方法的控制策略；Adam等［17］提出了多目标搜索的AS控制框架，并结合了强化学习与自诊断机制.Korkmaz等［18］采用随机搜索方法建立了一个多目标损伤容许度的控制策略.

在AS形状控制问题中，不同于维持形状或是微调结构的变形，定向运动是一类给定目标几何位置的形状控制任务，往往要求AS发生较大幅度的主动变形，且通常涉及到AS 的运动路径规划问题［19］.然而，基于随机搜索算法的主流控制方法依赖于AS的精确数值模型，而这就给AS 的定向运动带来了2个局限性：1）在没有任何学习机制的情况下，由于在决策过程中需要进行大量的非线性计算以搜索可行的执行解，故而限制了控制过程的实时性；2）在实际应用时，由于AS的数值模型往往与实际物理结构之间存在差异，因此基于模型的形状控制方法的效果也将受到限制.

针对AS定向运动及其路径规划问题，考虑到已有的基于随机搜索算法控制方法的局限性，本文以仿生思想为主要路线：提出AS的功能单元的概念，阐述大基本理论与仿生节律的形式；然后，建立含有功能单元AS的基本模型，同时推导了以索杆构件为主的AS的运动过程；再次，提出了基于功能单元的仿生控制框架；最后通过数值算例验证本文提出的概念及方法的可行性与效果.

1 主动结构的功能单元

1.1 传感器-执行器功能单元

主动结构（AS）主要包括传感器、执行器、控制器以及受力结构4个部分.在对AS的设计或分析中，一个核心的问题就是如何在控制以及仿真模拟的层面上将AS 的各个部分进行统一化的数值描述.借用有限元法的思想，AS的可控实体可以被看作是由有限数目的最小功能性单位构成的，每一个这样的最小单位包含一对或多对传感输入与执行输出，被称作是主动结构的功能单元（function element，FE）.

与有限元法描述的结构单元类似，功能单元的特点主要有：功能单元中的每一个传感器、执行器或控制器被认为是一个结点，且功能单元之间的连接区也被简化为结点；功能单元的结点分为输入结点与输出节点；对于某个功能单元来说，输入结点一般为传感器，代表着施加到功能单元上的“作用”，输出结点一般为执行器，代表功能单元在“作用”的刺激下产生的执行“效应”.一些简单的功能单元示例如图1所示，图中已将执行器与控制器合并为执行-控制器.

图1 主动结构的功能单元Fig.1 Function element of active structure

对于图1中的两结点单元，其“作用”与“效应”之间的关系可表示为

式中：a为执行器的总执行量（可表示为执行量增量的Δa形式）；s为传感器的采样值；c为控制器的传递系数.在结构的有限元法中，单元的作用（外力等）与效应（变形等）之间的关系由单元的刚度矩阵确定.在功能单元中，“作用”与“效应”之间的关系也可表示为类似的形式，将式（1）以矩阵的形式重写为

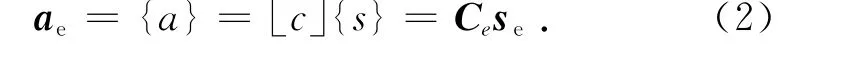
式中：ae为功能单元输出（执行）向量；se为功能单元输入（传感）向量；Ce为单元传递矩阵.对于图1中的四结点单元来说，其作用-效应关系可表示为

1.2 功能单元与功能结构

结构的有限元法将受力结构整体离散为有限个单元，与之类似，当单个功能单元或多个集成在一起的功能单元嵌入到AS中时，就构成了相对完整的结构，称之为AS的功能结构.在有限元法中，可按叠加法将单元刚度矩阵集成为整体刚度矩阵，类似地，设功能结构中包含nf个功能单元，对所有功能单元的单元传递矩阵进行扩大改写，就得到功能结构的整体传递矩阵为

对于整个功能结构来说，则有

式中：a为功能结构的执行器总执行量向量；s为功能结构的传感器测量值向量.只要各功能单元的作用-效应关系能够以式（2）表示，功能结构的整体传递矩阵就可以按式（4）集成.功能结构中的各个功能单元，可以是相互连接的，也可以是彼此独立的，一些功能结构的示例如图2所示.

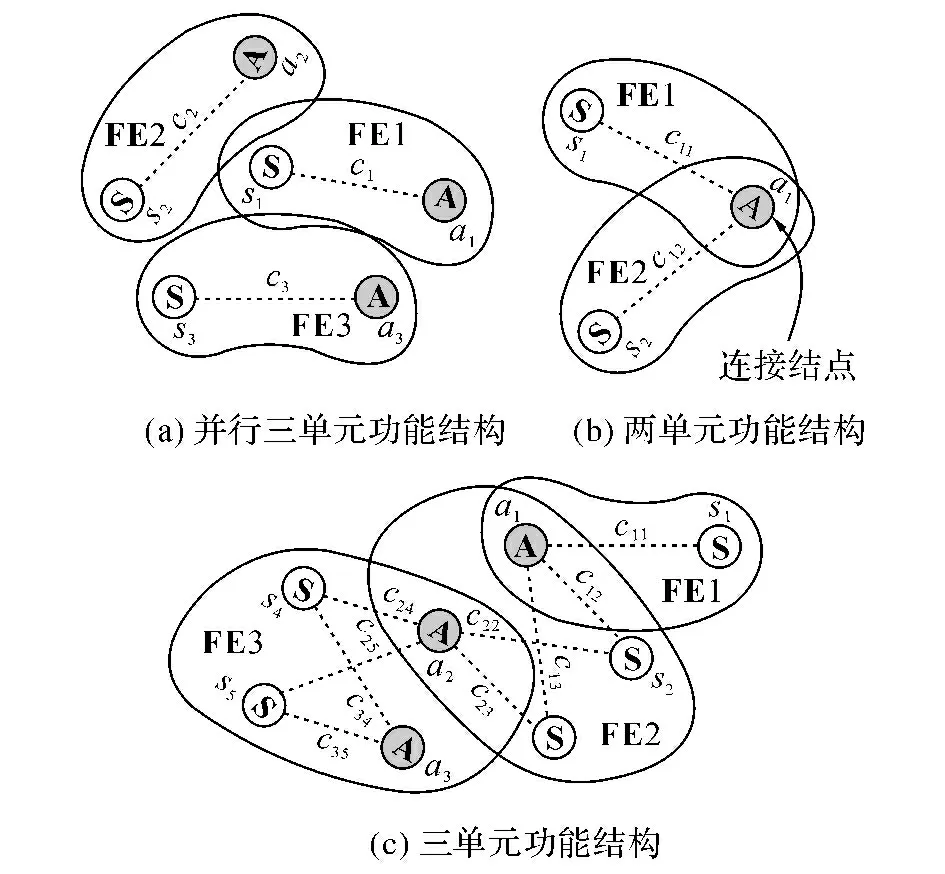
图2 主动结构的功能结构Fig.2 Function structure of active structure

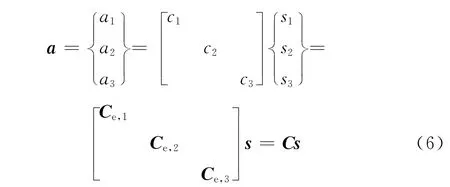
对于单元之间相互独立并行的功能结构来说，如图2（a）并行的三单元结构，将单元传递矩阵集成为整体传递矩阵，按式（4）、（5），有

有时，功能结构的输入结点与输出结点的数目并不一致，因此整体传递矩阵并不是方阵，对于图2右上的两单元结构，集成过程为

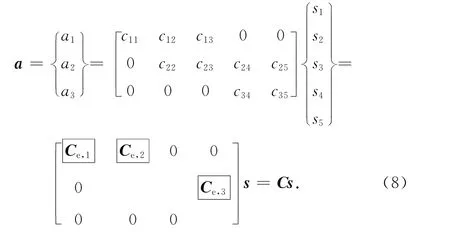
而对于图2中下侧的三单元结构，有

1.3 功能单元的节律

借用脊椎动物节律运动［20］的概念（如行走、奔跑、游泳、搔抓等），用以描述功能结构中周期性、重复性的单元反应，称作功能单元的节律.功能单元的节律通过预先设定的一系列固有的可重复时序，将功能结构中各功能单元的反应按照合理的次序、节律组合起来.若以一般化的形式表示，即将式（4）改写为

式中：整体传递矩阵C 是时间t 的函数；re，k为第k个功能单元的节律系数，同样是时间t的函数.

功能结构中的各个功能单元往往通过一定的相互激励或制约的关系形成稳定的节律模式，如图3所示中的并行功能结构所示，2个功能单元通过自我抑制与互相激发形成了稳定的等周期振荡节律，其整体传递矩阵为

若令

则

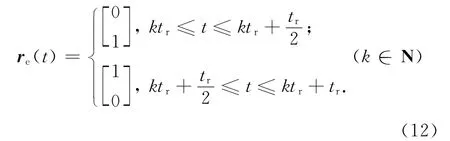
式中：tr为节律的周期.

2 含功能单元主动结构的基本模型

2.1 传感器的采样过程

布置在结构上的传感器负责收集相关物理量的数据，用以向控制器提供必要的反馈.传感器单次采样过程通常可表示为

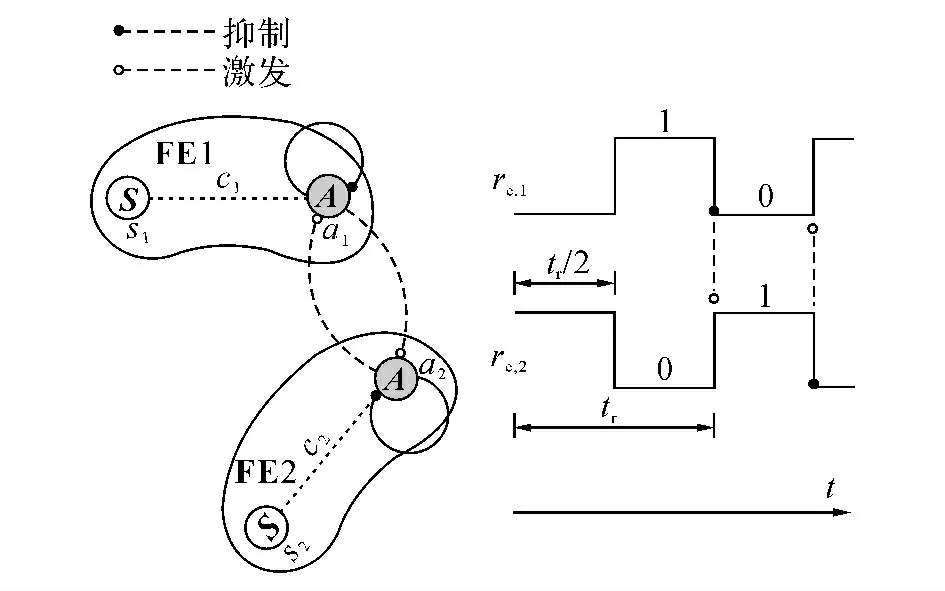
图3 功能单元的节律Fig.3 Rhythm of function element

式中：ps为可观侧物理量的真实值向量；es为传感器误差向量，一般与传感器分辨率、精度以及噪声干扰等因素有关；Λs为传感器布置矩阵，决定于传感器与相关物理量的对应关系.

一般来说，传感器测量对象以结构的位移与内力为主.在主动结构的形状控制中，传感器往往以结构的结点位移为测量对象，则式（13）可改写为

式中：d为主动结构的结点位移向量.

2.2 控制器的输出与执行器的执行过程

传感器将采得的数据反馈到控制器，控制器根据实际的有效数据，按照预先设定的规则输出相应执行器的动作方案，对于单个功能单元来说，这一过程可表示为如式（2）、（3）的形式，对于整个功能结构来说，这一过程即式（5）.

附着在构件上的执行器按照控制器的输出，将相应的执行量施加于主动结构，从而影响结构的相关物理量，其一般过程可以描述为增量的形式

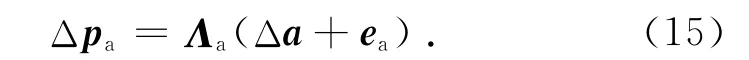
式中：pa为可被执行器直接改变的物理量真实值向量；ea为执行器误差向量，主要与执行器分辨率、精度以及随机误差等有关；Λa为执行器布置矩阵，决定于执行器与相关物理量的对应关系.

执行器可以作用于主动结构的形状，这样，结点位移就是执行器直接影响的对象，即式（15）可以改写为

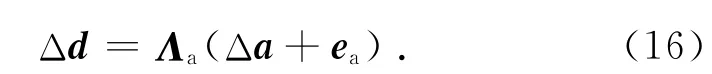
更多时候，执行器是作为结构中的主动构件的一部分产生作用的，主动构件可以通过输出内力变化或长度变化.以主动杆（或索）构件为例，若执行器输出内力变化时，即式（15）可以改写为

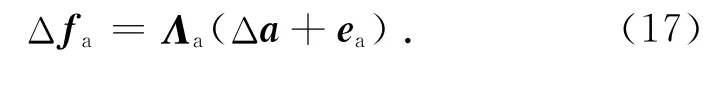
式中：fa为结构构件的轴向内力.比较常见的情况是，主动构件往往以自身的自由状态下长度（静息长度）为参照输出长度变化，即式（15）又可改写为

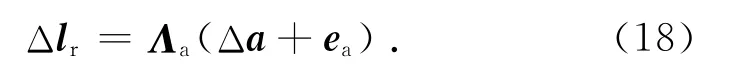
式中：lr为结构构件的静息长度向量.

2.3 结构的运动过程

以式（18）为主要讨论情况，以索杆结构为例，主动构件在参与受力的同时，其动作后的实际长度变化与其精细长度变化往往是不一致的，若以对数应变的形式表示构件单元的轴向应变，则有

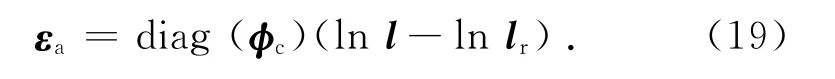
式中：εa为结构杆（或索）构件的轴向应变向量；l为结构杆（或索）构件的实际长度向量；φc为索单元应变修正因数向量（若单元k 为索单元，且lk＜lr，k，则φc，k＝0；否则φc，k＝1）.从而，构件的轴向内力为

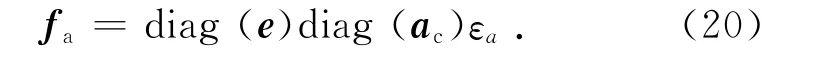
式中：e为杆（或索）构件弹性模量向量；ac为杆（或索）构件的横截面积向量.

若主动结构为几何不变时，其结点内力向量与结构整体刚度有关，即

式中：fi为结点内力向量；K 为结构整体刚度矩阵.有时，在不方便集成K、或需要对K 求逆而K 恰巧为奇异（如边界条件不充分时）等情况下，可直接在结构构件单元层面直接将内力整合叠加为结点内力［21］，即

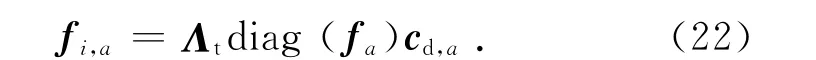
式中：fi，a为结点内力在空间a 轴（x，y 或z轴）方向上分量的向量；cd，a为杆（或索）构件方向余弦在a 轴方向上分量的向量；Λt为索杆结构的拓扑矩阵，决定于结构中结点与构件单元间的连结关系（若结点i是构件单元j 有向线段的起点，则λt，i，j＝1；若是终点，则为-1；其他，则为0）.

主动结构的运动方程遵循牛顿第二定律，在a轴方向上

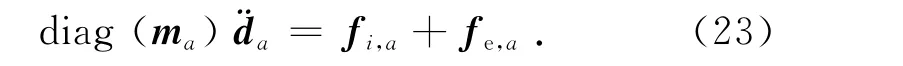
式中：ma、da和fe，a分别为a 轴方向上的结点质量向量、结点位移向量与结点外力向量.

3 基于功能单元的仿生控制框架

大多数脊椎动物的运动主要涉及到3套系统，即感觉系统、运动系统与神经系统［22］.类似地，以脊椎动物作为模仿对象，设计一个基于功能单元的控制框架，如图4所示.

图4 含功能单元的主动结构的仿生控制框架Fig.4 Bio-inspired control framework of active structure with function element

图4控制框架中的主要参与者包括各个分布的功能单 元 的 执 行-控 制 器（distributed actuator and controller，DAC）、分布的传感器（distributed sensor，DS）以及受力结构.该控制框架构成了一个闭合环路，即受力结构（躯体）→DS（感受器）→DAC（脊髓与效应器）→受力结构（躯体），也就是说，形成了虚拟的“反射弧”.在整个主动结构中，可以存在多个这样的反射弧环路，而承载这些环路的具体形式就是功能单元.

在基于功能单元的控制框架中，由于控制过程并不依赖于主动结构的有限元数值模型，控制系统（也就是功能结构）不需要通过大量的计算求解控制方案，因此，在没有可参照学习的案例的情况下，整个控制过程的实时性将优于基于模型的结构控制方法.这一控制过程的基本单位就是功能单元的反应，如图5所示，在功能单元中的每一反应过程为：DS在DAC的触发下对结构的相关物理量进行采样；DS采样完成将数据回传至DAC；DAC 根据回馈数据决定执行量；DAC 将决策的执行量施加到结构上.图中和时间相关的几个参数有：数据传输耗时tt；DAC决策耗时tc；传感器采样耗时ts；DAC 的执行耗时ta.

图5 功能单元的反应Fig.5 Response of function element

4 算例分析

4.1 主动结构的定向运动

采用与文献［19］中相似的算例，如图6所示，一主动张拉整体结构，高度与宽度均为3m，包含4结点、2撑杆、4拉索，结构在结点N1与N2处有简单支承.定向运动要求结点N4从其初始位置移动至N4′，即撑杆M6绕结点N2 逆时针旋转10 后的位置.与文献［19］中算例不同的是，撑杆的刚度并非无限大，在内力作用下将发生轴向变形.

主动张拉整体结构的撑杆（M5与M6）弹性模量206GPa，等效截面积621.25mm2，0时刻初始应力为0.拉索（M1～M4）弹性模量150GPa，等效截面积28.27mm2，0时刻初始预应力为1 MPa.所有构件均为钢材，密度为7 850kg／m3，具备足够的强度.环境中质量阻尼系数为30s-1，无重力，模拟时采用文献［21］中的以中心差分法为主的向量式有限元法，时间步长取为8×10-4s.

在主动张拉整体结构中，结点N4 处布置了双轴位移传感器S1，可同时测量x 与y 轴方向的位移，分辨率为0.01mm，无噪声.拉索M3与M4为主动构件，嵌入了可调节长度的DAC，即A1与A2，固定速率为0.5m／s，最小刻度为0.01mm，无额外干扰.所有设备之间依赖于无线信号进行通信，单次无线传输耗时0.005s，无丢包，所有设备的硬件处理时间忽略不计.

对于主动张拉整体结构来说，其功能结构的布置如图6 所示，2 个功能单元连结于S1，并构成自抑-互激的交替节律.考虑到定向运动目标需分解到各功能单元，对于功能单元k 来说，其作用-效应关系可由式（1）改写为

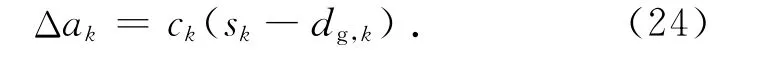
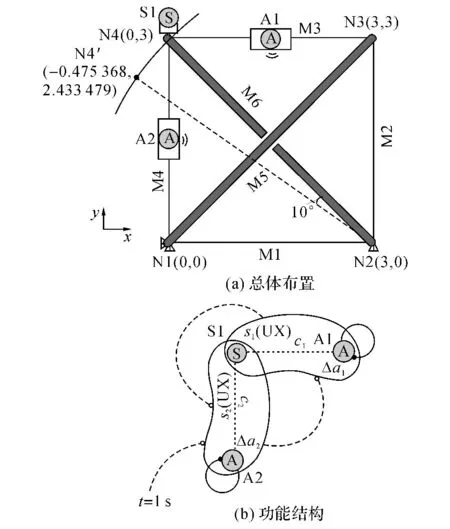
图6 主动张拉整体结构：初始布置Fig.6 Active tensegrity：Initial layout

式中：dg，k为功能单元k的目标位移.对于本例，c1与c2分别为0.2与-0.2，dg，1与dg，2分别为-0.475 368与-0.566 521m.功能结构在t＝1s时刻开始激活，并从功能单元2发起，进入运动过程.

在主动张拉整体结构的定向运动过程中，部分物理量随时间t的变化如图7、8 所示.图中UX与UY分别表示结点在x 与y 轴方向上的位移，ACT表示DAC 的总执行量（＋／-分别表示伸长／收缩）.可以看出，在定向运动过程中，A1 与A2 分别伸长与收缩，结点N4各向位移在较早的时间就已渐进平缓.

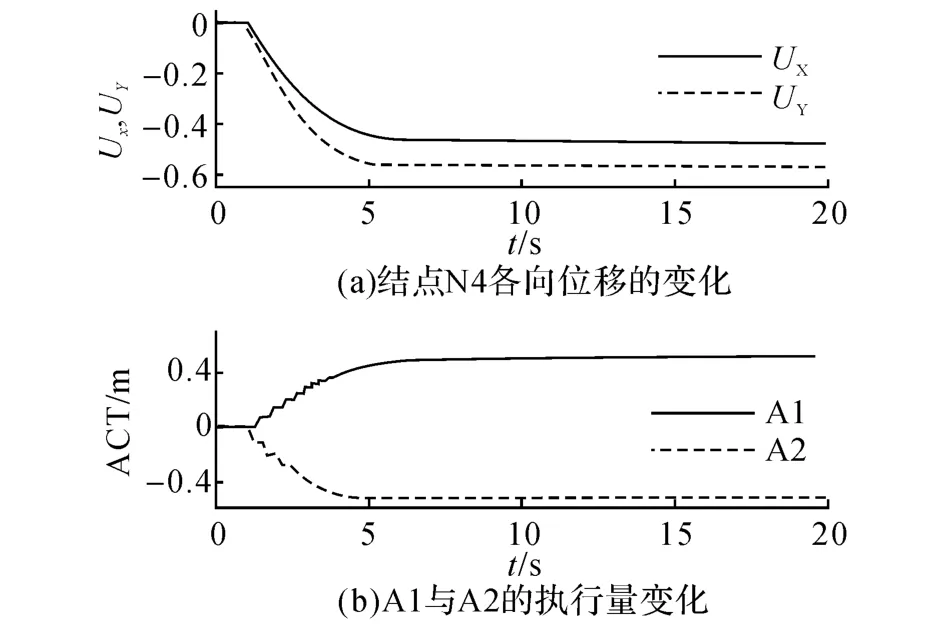
图7 主动张拉整体结构：定向运动过程的物理量变化Fig.7 Active tensegrity：Variation of physical quantities during orientation movement

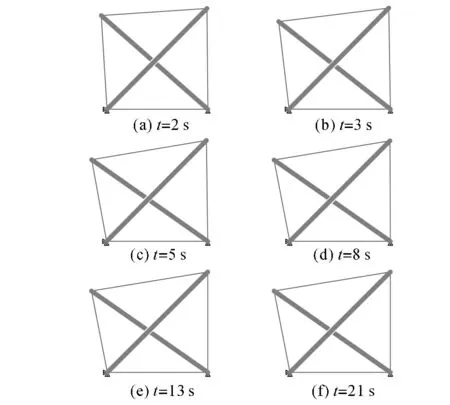
图8 主动张拉整体结构定向运动过程Fig.8 Orientation movement of active tensegrity

在主动张拉整体结构定向运动过程中，上侧两结点在t＝0～15s时间段的运动轨迹如图9所示，图中不同灰度代表了时间的变化.可以看出，结点N4约在t＝5s左右就已接近了目标位置，随后较长的时间花费在对结点位置的微调，其整个运动路径近似于起始位置与目标位置相连的直线段.结点N3从其初始位置出发，经过近似直线的移动至最高点，继而返回其初始位置附近，最终稳定位置略高于初始位置.

对于主动结构形状这类非线性受控对象来说，多数情况下通过线性的功能单元的传递系数（或矩阵）就可以完成相应的控制功能，如式（24）.功能单元的传递系数（或矩阵）表征了功能单元自身的状态特性，而对于整个闭环控制系统来说，则是起到了状态反馈的作用.

图9 主动张拉整体结构定向运动过程中的结点轨迹Fig.9 Node trail of active tensegrity during orientation movement

4.2 非线性功能单元——多运动目标与障碍物规避

主动结构的定向运动往往存在着附加的控制约束条件，而这些约束条件可能同样是指定的形状控制目标，也可能是对外部环境对运动路径的约束，如需要避免对障碍物的接触或碰撞.按照文献［19］中算例设定，在上一例的基础上为主动张拉整体结构增加了障碍物，如图10所示，障碍物出现在结点N4的运动方向上，障碍物右下角位于角∠N4-N2-N4′的平分线上，与线段N4-N4′的中点相距0.06 m.同时，由于图9中显示定向运动结束后，结点N3最终位置的高度与初始高度产生一定的偏离，故此处提出一附加运动目标，即令N3的高度尽可能保持在其初始高度附近.要求结点N4在不接触障碍物的前提下，实现原定的定向运动目标，并实现N3的附加控制目标.同时按文献［19］设定M5 与M6为刚性撑杆，此处使其轴向刚度（弹性模量与等效截面积的乘积）增大至原刚度的1 000倍，具体令弹性模量增大为2.06×104GPa，截面积增大为6 221.5 mm2，且密度也相应增大为7.85×105kg／m3.

如图10所示，主动张拉整体结构在图6的基础上，增添一个DS（即S2）与DAC（即A3），S2为单向位移计，用于测量结点N3的竖向位移，A3 嵌入在拉索M2中.对于本例中的多目标控制以及障碍物规避的要求，则需要对运动目标进行更为细致的分解.主动张拉整体结构的功能结构如图11所示，A1～A3所在的功能单元分别负责N4在x 轴、N4在y 轴、N3在y 轴 的 运 动 控 制.

考虑到障碍物的影响，由于N4 在定向运动路径上首先面对障碍物的右侧边界，故考虑将避开障碍的控制任务交由A1所在功能单元负责，此时，A1所在功能单元需要同时以N4的x 与y轴位移传感数据作为输入“作用”，因此变为了一个双输入-单输出的功能单元（图11）.

按一般功能单元的线性关系（见式（2）与（3）），A1所在功能单元的作用-效应关系可表示为

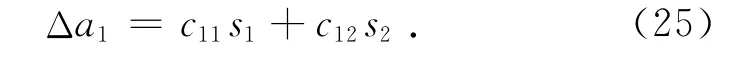
而对于障碍物的规避判断，作用-效应关系将成为非线性时变关系，且判断过程涉及S1的y轴位移传感数据（即s2），因此，上式应改写为

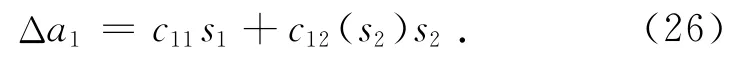
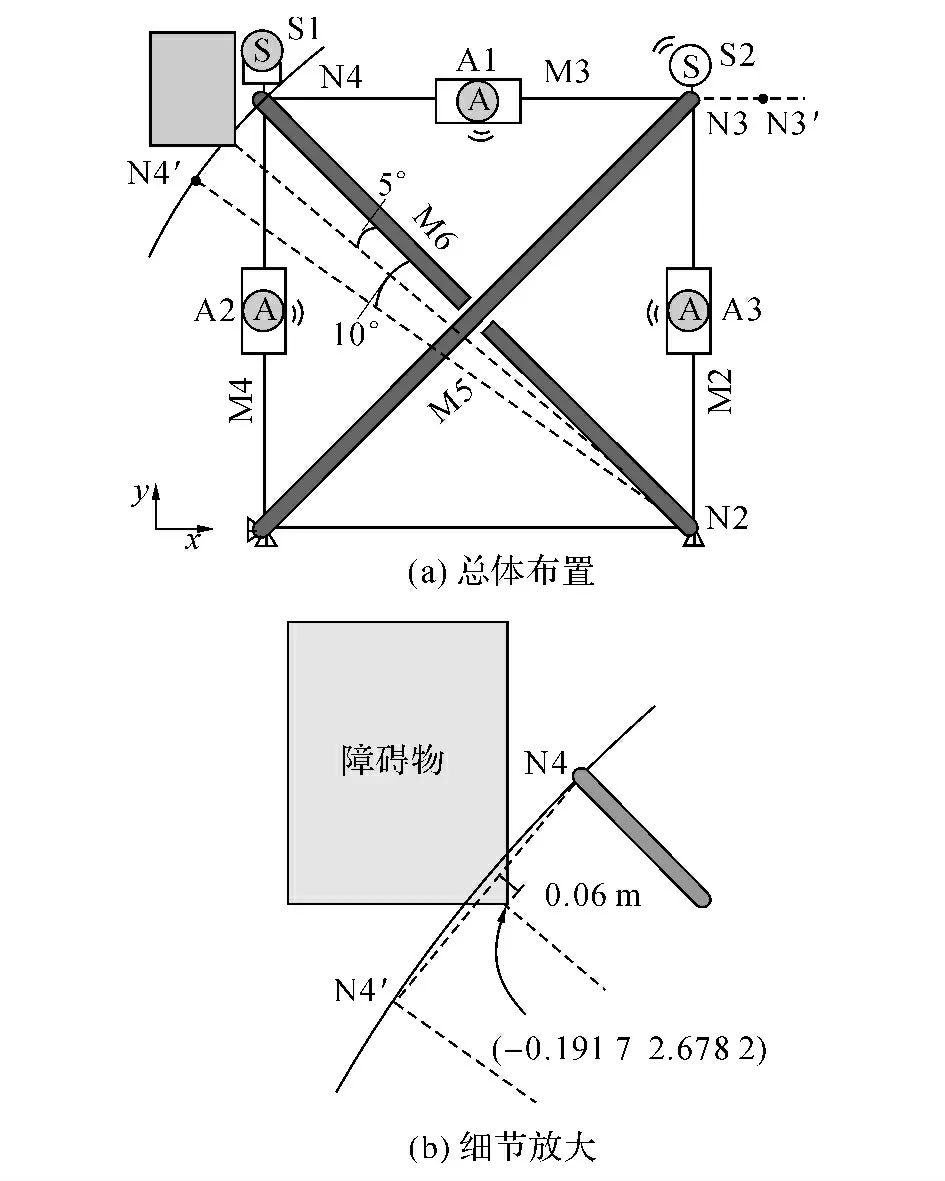
图10 主动张拉整体结构：附加目标以及障碍物Fig.10 Active tensegrity：Additional object and obstacle

图11 主动张拉整体结构：非线性功能结构Fig.11 Active tensegrity：Non-linear function structure

此时，A1所在功能单元就具备了非线性的作用-效应关系，而这一关系与式（24）的本质是相似的，不同的是，A1所在功能单元的目标位移值dg，1′将随S1的y轴位移值的变化而变化：当结点N4高于障碍物下缘时，dg，1′以障碍物的右侧边缘为准；当N4低于障碍物下缘时，dg，1′为原定的dg，1.因此式（26）可按式（24）改写为

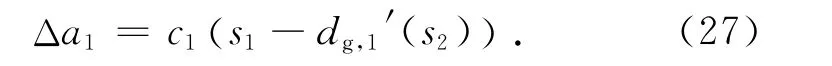
而同时

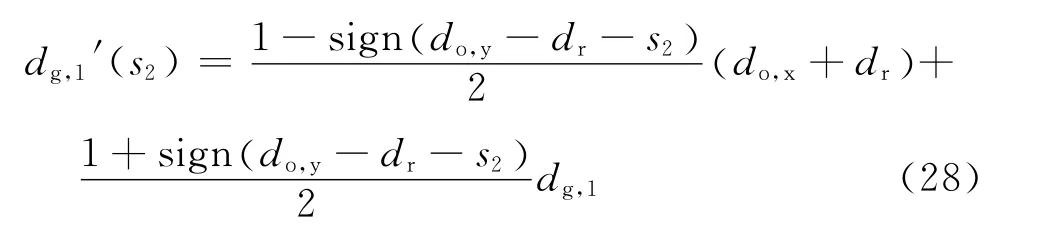
式中：do，x与do，y分 别 为 障 碍 物 的 右 下 角 点 到 结 点N4初始位置的有向距离在x 轴与y 轴的分量；dr为靠近障碍物的保留距离（设定dr的主要目的在于，围绕障碍物外侧周围制造一个临界区域，从而充当与障碍物靠近的第一道缓冲区域）.本例中，do，x与do，y分 别 为-0.191 7 m 与-0.321 8 m，dr＝0.03m；A3 所在功能单元的反应关系同样遵循式（24），并设定c3＝-0.2，dg，3＝0.

从主动张拉整体的在躲避障碍过程的运动结果（图12与13）中可以观察到，结点N4的运动路径成功避开了障碍物，并且达到了指定目标位置.同时，由于躲避障碍的需要，结点N3在定向运动的过程中有更为明显的位置偏移，当然最终恢复到了距初始位置高度更接近的位置.与文献［19］原例中836.7s的计算时间相比，本例中AS运动的全部耗时少于20s.

当主动结构的形状控制问题较为复杂或涉及到多目标任务时，功能单元的传递系数（或矩阵）可按照实际需要设计为非线性，其取值可按一定机制随受控系统状态变量的改变而改变，如本例中非线性功能单元中的作用-效应关系.

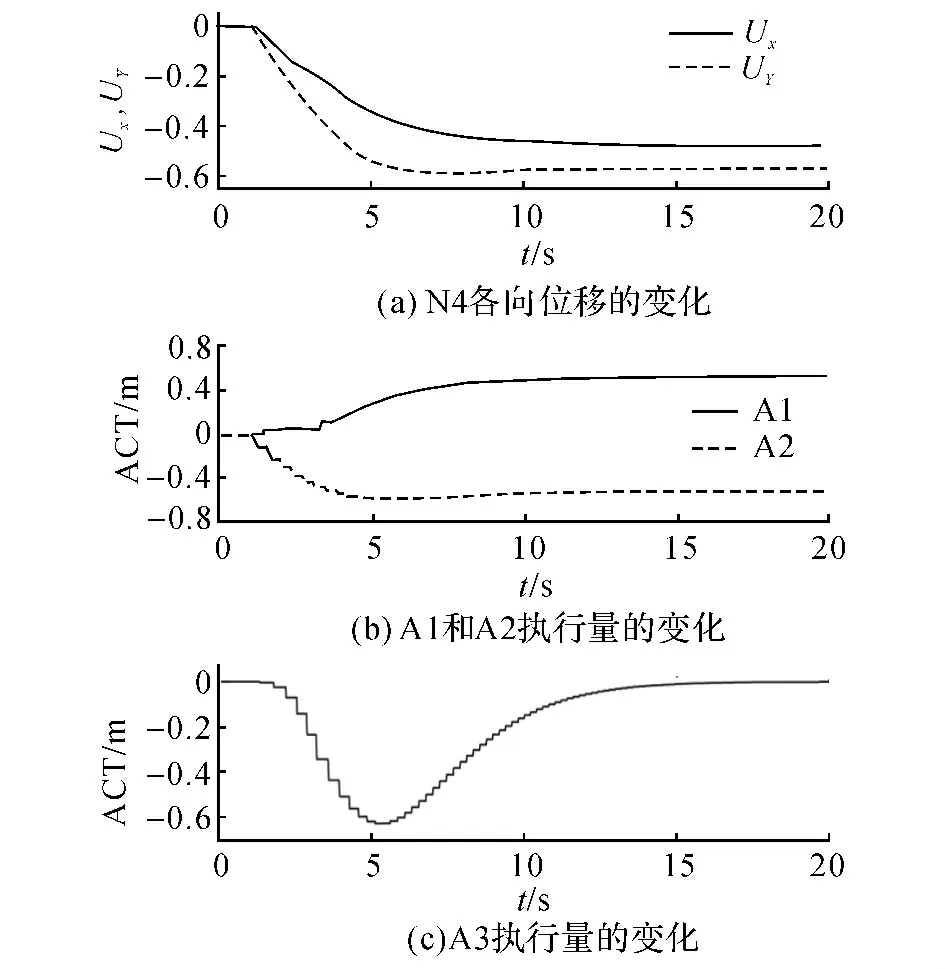
图12 主动张拉整体结构在多目标障碍物规避定向运动中的物理量变化Fig.12 Variation of physical quantities of active tensegrity during multi-objective collision-free orientation movement

5 结 论

图13 主动张拉整体结构在多目标障碍物规避定向运动中的结点运动轨迹Fig.13 Node trail of active tensegrity during multi-objective collision-free orientation movement

（1）本文提出了功能单元的概念，并建立了相应的含功能单元主动结构的基本模型.不同于传统研究思路的主动结构架构方法，其意义在于，将控制系统与受力结构同等对待并统一起来，以类似有限单元法的方式对其控制过程进行设计与分析，从而可以在实际控制过程中不依赖于对结构数值模型的求解.

（2）相比传统基于模型的控制方法，本文提出的无模型仿生控制框架减少了误差来源，即，不会由于数值模型与实际结构的差异而影响控制效果，控制过程的精度仅由传感器决定.

（3）传统基于模型的控制方法在执行控制方案前一般将消耗较长时间进行搜索求解，本文提出的仿生控制框架避开了这一过程，整个控制过程是即时反应的，从而提高了实时性.另一方面，由于计算量极小，对硬件设备性能的要求也是非常低的，也就是说，在控制过程中，完全可以用成本低廉的单片机代替PC机.

（4）本文提出的基于功能单元的仿生控制方法可以作为传统基于模型的控制方法的一种补充，或是某些场合下的辅助手段，其优点在于无需外部环境作用的信息（如荷载条件等）.

在实际应用时，主动结构往往是非理想的复杂结构体系，可能受到外部环境的复杂作用，如接触、碰撞、不规律荷载等，也可能受到来自内部材料性能影响，如塑性、预应力松弛、构件损伤等，如何在这些复杂条件下采用功能单元实现主动结构形状控制，将是本文进一步研究的方向.

（

）：

［1］SOONG T，MANOLIS G.Active structures［J］.Journal of Structural Engineering，1987，113 （11）：2290-2302.

［2］YAO J T.Concept of structural control［J］.Journal of the Structural Division，1972，98（7）：1567-1574.

［3］SHEA K，FEST E，SMITH I F C.Developing intelligent tensegrity structures with stochastic search ［J］.Advanced Engineering Informatics，2002，16 （1）：21-40.

［4］NOAK T，RUTH J，M LLER U.Adaptive hybrid structures［C］∥Proceedings of the International Conference on Adaptable Building Structures.Eindhoven，Netherlands：International Council for Research and Innovation in Building and Construction，2006，256-260.

［5］SHEN Y B，CHENG H Q，YANG P C，et al.A static control algorithm for adaptive beam string structures based on minimal displacement［J］.Mathematical Problems in Engineering，2013，2013（2013）：1-10.

［6］KAWAGUCHI K-I，HANGAI Y，PELLEGRINO S，et al.Shape and stress control analysis of prestressed truss structures［J］.Journal of Reinforced Plastics and Composites，1996，15（12）：1226-1236.

［7］DJOUADI S，MOTRO R，PONS J，et al.Active control of tensegrity systems［J］.Journal of Aerospace Engineering，1998，11（2）：37-44.

［8］ KANCHANASARATOOL N， WILLIAMSON D.Modelling and control of class NSP tensegrity structures［J］.International Journal of Control，2002，75（2）：123-139.

［9］FEST E，SHEA K，DOMER B，et al.Adjustable tensegrity structures［J］.Journal of Structural Engineering，2003，129（4）：515-526.

［10］ZHANG S X，DU J L，DUAN B Y，et al.Integrated structural-electromagnetic shape control of cable mesh reflector antennas［J］.AIAA Journal，2015，53（5）：1395-1398.

［11］沈黎元，李国强，罗永峰.预应力索结构位移控制［J］.同济大学学报：自然科学版，2006，34（03）：291-295.SHEN Li-yuan，LI Guo-qiang，LUO Yong-feng.Displacement control of prestressed cable structures［J］.Journal of Tongji University：Natural Science，2006，34（03）：291-295.

［12］肖南，肖新，董石麟.张力结构形状调整优化分析［J］.浙江大学 学报：工 学版，2009，43（08）：1513-1519.XIAO Nan，XIAO Xin，DONG Shi-lin.Shape optimization analysis of tensegrity structure［J］.Journal of Zhejiang University：Engineering Science，2009，43（08）：1513-1519.

［13］徐伟炜，吕志涛，丁汉山.基于开关控制的智能预应力结构模型试验［J］.工程力学，2011，28（05）：105-110.XU Wei-wei，LU Zhi-tao，DING Han-shan.Model experiment of smart prestressed structures based on switch control［J］.Engineering Mechanics，2011，28（05）：105-110.

［14］DOMER B，SMITH I.An active structure that learns［J］.Journal of Computing in Civil Engineering，2005，19（1）：16-24.

［15］XU X，LUO Y.Multi-objective shape control of prestressed structures with genetic algorithms［J］.Proceedings of the Institution of Mechanical Engineers，Part G：Journal of Aerospace Engineering，2008，222（8）：1139-1147.

［16］FEST E，SHEA K，SMITH I.Active tensegrity structure ［J］.Journal of Structural Engineering，2004，130（10）：1454-1465.

［17］ADAM B，SMITH I F C.Active tensegrity：A control framework for an adaptive civil-engineering structure［J］.Computers ＆ Structures，2008，86 （23／24）：2215-2223.

［18］KORKMAZ S，ALI N B H，SMITH I F C.Configuration of control system for damage tolerance of a tensegrity bridge ［J］.Advanced Engineering Informatics，2012，26（1）：145-155.

［19］XU X，SUN F，LUO Y，et al.Collision-free path planning of tensegrity structures［J］.Journal of Structural Engineering，2013，140（4）：04013084.

［20］SQUIRE L R.Fundamental Neuroscience［M］.San Diego：Academic Press，2013.

［21］TING E C，SHIH C，WANG Y-K.Fundamentals of a vector form Intrinsic finite element：part i.basic procedure and a plane frame element［J］.Journal of Mechanics，2004，20（02）：113-122.

［22］STARR C，TAGGART R，EVERS C，et al.Biology：The Unity and Diversity of Life［M］.Belmont，CA：Cengage Learning，2008.