基于GA-PSO的粗糙集属性约简算法*

戴上平，刘素军，郑素菲

(华中师范大学计算机学院，湖北 武汉 430079)

1 引言

粗糙集理论[1]是一种新的数学理论，用于处理不准确和不完整的数据。它已被广泛应用在人工智能、知识和数据发现、模式识别和分类、数据分析和其他不精确推理的方面。其通过知识约简导出问题的决策或分类规则来保持稳定的分类能力。在该理论中属性约简是一个核心问题，它是指信息系统在保持能力或知识的归类决定没有改变的同时，删除不重要的或不相关的属性。

遗传算法GA(Genetic-Algorithm)具有隐含并行性、鲁棒性、可扩展性等优点，擅长全局搜索，除了适应度计算外，几乎所有的遗传操作都建立在全局统计处理的基础上。这样使得全局的重复计算量大且易“早熟”。遗传算法在属性约简过程中采用不同的编码方法，会产生不同的问题，从而导致没有根据的积木假设，最终使得属性约简时GA过早收敛难以达到全局最优。粒子群优化PSO(Particle-Swarm-Optimization)算法是一种通过用无质量无体积的粒子作为个体，同时为每个粒子提供简单行为规则使整个粒子群呈现出一定特性，以解决复杂的优化问题的进化计算技术。

在粗糙集属性约简[2]中，GA与PSO在进化过程中均能保留和利用位置的信息，但除此之外，PSO算法还能利用速度(即位置的变化过程)信息，使得PSO比GA收敛于最优解的速度更快。粒子群约简算法过程中，粒子群在迭代时容易陷入到局部极值点中，导致得不到全局最优解，使得最后的约简结果不是最小相对属性集。针对遗传约简与粒子群约简的不足，本文提出了一种新的约简算法，即：基于GA-PSO的粗糙集属性约简算法。

2 粗糙集基本知识与GA、PSO的引入

2.1 常用粗糙集基本定义

定义1设S=(U,A,V,F)为一个信息系统，又称知识表示系统。其中，U={U1,U2,…,U|U|}为论域对象空间，U是有限非空集合，称为；A={ɑ1,ɑ2,…,ɑ|A|}为属性的有限非空集合；V=∪Vɑ，其中ɑ∈A，Vɑ为属性ɑ的值域；F：U×A→V为信息函数，对于∀ɑ∈A、∀x∈U，F(x,ɑ)∈Vɑ，它指定了U中每一对象的属性值。若A中的属性又可分为两个不相交的子集，即条件属性集C和决策属性集D，即：A=C∪D,C∩D=∅，则S称为决策表。

定义2给定一个知识表示系统S=(U,A,V,F)，P⊆A，X⊆U，x⊆U，集合X关于I的下近似、上近似、负区及边界区分别为：

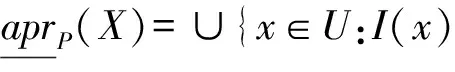
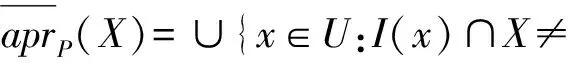
negP(X)=∪{x∈U:I(x)∩X≠∅}

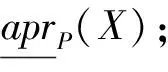
定义3设知识表达系统S=(U,A,V,F)，A=C∪D,C∩D=∅，条件属性C对决策属性D的支持度(决策属性D对条件属性C的依赖度)定义为：

(1)

式(1)称D在K程度上依赖于C，其中|·|指集合包含的元素个数，一般取0≤K≤1。当属性集中的属性值决定着属性的所有属性值时，本文把K取值为1；当属性集中的属性值决定着属性中的部分属性值时，K的取值范围小于1。

定义4若S=(U,A,V,F)是一个知识表达系统，当B为C的一个(相对于决策属性D的)相对约简时，应满足条件：B⊆C，若KB=KC，且不存在R⊆B，使得KR=KB，此时约简结果可能有多个。相对约简的集合记为redD(C)，所有C属性约简的交集记为Core(C)(又称C的核)，且有CoreD(C)=∩redD(C)。最小约简指含有最少属性的约简。

2.2 遗传算法

2.2.1 染色体编码

遗传算法[3]的解集是从经过基因编码的一定数目个体组成的一个种群开始，该种群中的各个体以染色体为载体，采用固定大小的二进制串表示其基因值。长度为15的染色体可用Y=110100101011001来表达。

2.2.2 选择操作

从种群中选择出质量优的个体使之作为父代再生优化同时淘汰劣质个体的操作称为选择操作。轮盘赌方法选择算子是传统的遗传属性约简中的选择运算，在该操作中，各个体的选择概率和其适应度值成比例，其适应度值比例越大，该染色体代表的种群个体被选择交配的机会也越大。

2.2.3 交叉操作

交叉操作是把两个父代个体的部分结构加以替换重组而生成新的个体。交叉运算根据交叉率将种群中的两个个体随机地交换某些基因，能够产生新的基因组合。在使用单点交叉操作中，从个体串中随机设定一个交叉点，实行交叉时，该点前或后的两个个体的部分结构进行互换，并生成两个新的染色体个体。该处用到的双亲染色体由轮盘赌方法随机选出，参照依据是每个染色体适应度值。

2.2.4 变异操作

变异操作是对群体中的个体串的某些基因座上的基因值作变动。其目的是保证遗传操作具有局部搜索能力的同时又要维持群体的多样性，进而保证在加速向最优解收敛的同时又能防止出现未成熟收敛。常用的变异运算是根据变异概率Pm随机选择染色体的个体，实现在某些位置进行0，1翻转。

2.3 粒子群算法

粒子群算法的数学思想为：在D维搜索空间中，有一个群体由m个粒子组成，第i个粒子(i=1,2,…,m)的位置表示为Xi=(χi1,χi2,…,χid)，速度表示为Vi=(υi1,υi2,…,υid)。第i个粒子搜索到的最优位置为Pbesti=(ρbesti1,ρbesti2,…,ρbestid)，整个粒子搜索到的最优位置记为Gbest=(gbesti1,gbesti2,…,gbestid)。综上定义，粒子群算法的进化方程描述为：

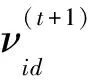
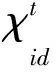
(2)

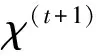
(3)

其中，i= 1,2,…,m;d= 1,2,…,D;t为当前迭代次数;惯性权重ω取非负常数;τ1、τ2为加速因子,取非负常数，用来调节粒子向全局最优粒子和个体最优粒子方向飞行的步长;γ1、γ2为[0,1]内两个相互独立的均匀分布的随机函数。

3 GA-PSO属性约简算法

3.1 编码方法

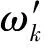
ωk=KCore(C)∪ck-KCore(C)

(4)

(5)

属性ck的对应位lk取0或1由公式(6)决定：

(6)

即将属性编码为粒子。

3.2 粒子适应度函数

适应值函数的形式决定着群体的进化行为，也是对粒子的适应性进行评价的唯一确定指标。为控制粒子朝着约简的方向发展，保证所得到的粒子是一个约简。本文定义适应度函数与平均适应度函数如下：

Fitness(P)=k1*(KP/KC)+k2*(1-KP)

(7)

(8)

其中，k1的大小决定着待约简粒子适应值的大小，与之成正比。种群中优良粒子保留下来的概率越大，其对应的取值也越大。而函数属性数目的大小或者约简属性数目的大小由k2判定，其值越大，它的适应度值也越大。式(9)决定k1与k2的大小。当KP/KC的值为“1”时，得到的属性集是一个约简。

(9)

3.3 遗传操作与粒子更新

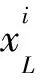
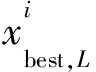
(10)

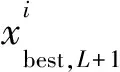
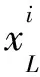
(11)

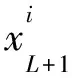
(12)

权重因子τ1、τ2和随机数γ1、γ2决定变异的程度与方向，式(12)使得变异有了学习能力。

3.4 局部最优与全局最优

局部最优是个体极值，即粒子在迭代更新过程中自身所找到的最优解。全局最优则是全局极值，即整个种群在进化迭代中所找到的最优解也就是适应度值最好的一个位置。在GA-PSO算法中，局部最优需要与粒子新的适应度值进行比较，由式(13)决定。全局最优为种群中最优质粒子，按式(14) 与每个粒子的局部最优进行比较求得。

Pbesti=max(Pbesti,Fitness(i))

(13)

Gbest=max(Pbesti,Gbest)

(14)

3.5 GA-PSO约简算法执行过程

输入：一个决策表S=(U,A,V,F)，A=C∪D，C是条件属性集，D是决策属性集。

输出：此决策表最小相对属性约简。

步骤1由式(1)计算出决策属性D关于条件属性C的支持度KC(D)；

步骤2令Core(C) =∅，逐个去掉一个属性c∈C，若KC-c≠Kc，则Core(C)=Core(C)∪{c}。若KCore(D) =Kc(D)，则Core(C)即为最小相对约简。否则，转步骤3。

步骤3初始化粒子。除去核属性，由式(4)计算其余各属性权重，并把求得的权重按照公式(5)映射到[0,1]，根据公式(6)初始化各粒子，设置最大迭代次数T=80。

步骤4更新粒子群。由式(7)计算第i个粒子在t时刻的适应值Fitness(i)，由式(8)计算当前种群的平均适应度AF。由式(11)和式(12)更新粒子位置，由式(13)更新局部最优值，由式(14)更新全局最优粒子，取种群中粒子最优适应度为全局最优粒子。

步骤5将种群中每个粒子的适应度值与当前种群的AF值进行比较，适应度大于AF的粒子给予保留，适应度小于AF的粒子，用上面提到的均匀交叉法交叉、变异操作到变异算子。

步骤6判断是否满足终止条件，若达到最大迭代次数或所求得的结果不再发生变化，则终止迭代，否则转步骤4。

4 实验结果及分析

为了验证本文算法(记为GA-PSO属性约简)的有效性和正确性，本文用UCI机器学习数据库中的标准数据集作为测试数据，从UCI数据库中分别选取具有低、中、高维特征的Iris、Zoo、Sogbeanbarge三个数据集作为算例进行计算，并同文献[5]的基于遗传算法的粗糙集属性约简算法(记为GA属性约简)与文献[6]的基于粒子群优化算法的粗糙集属性约简(记为PSO属性约简)在属性约简过程中适应度值和计算平均时间开销两方面进行比较。

对本文提出的GA-PSO算法，参数值分别取变异概率Pm=0.2，交叉概率Pc=0.75，m=25，在Windows7、内存为2 GB的PC机上运行10次;GA约简算法与粒子群约简算法参数设置参照参考文献[5,6]，最大迭代次数均设置为80。三组实验均在同一台PC机上运行，求得最小相对属性约简集与平均运行时间。三种算法的属性约简结果如表1所示，为了更好地呈现出进化过程，图1给出了具体进化过程中的适应度值曲线；为了观察收敛速度，图2给出了三种算法进行相同迭代次数的约简实验10次的运行时间曲线图。

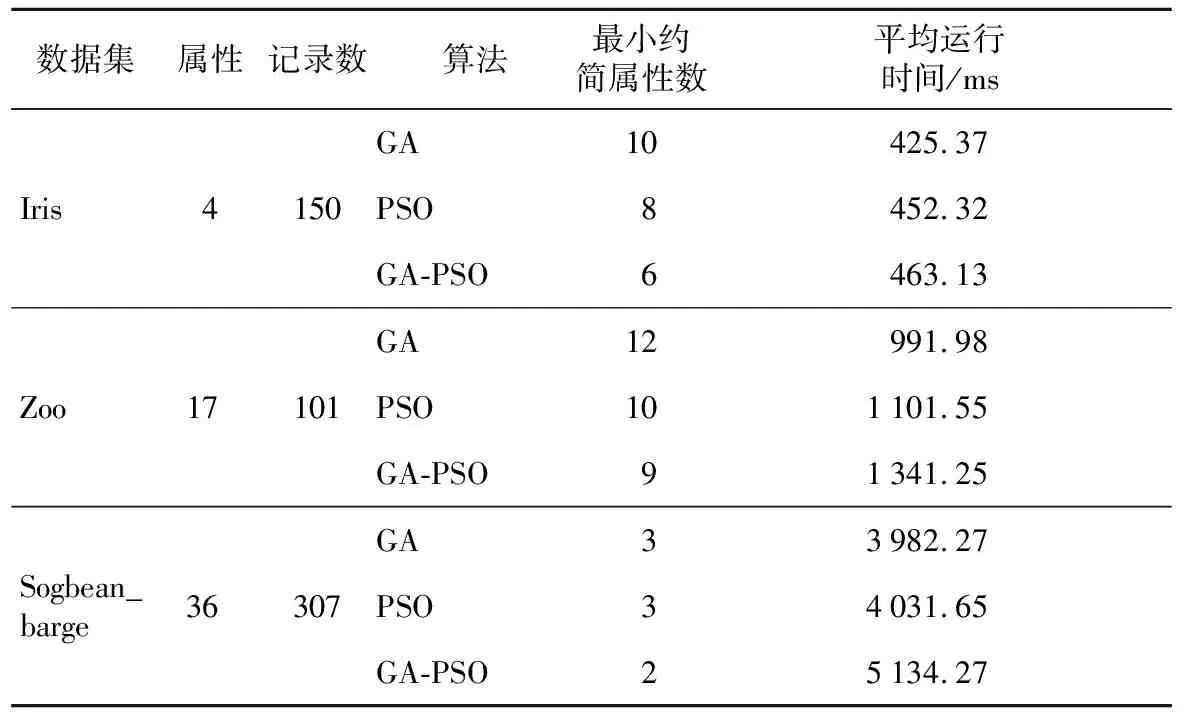
Table 1 Results of attribute reduction

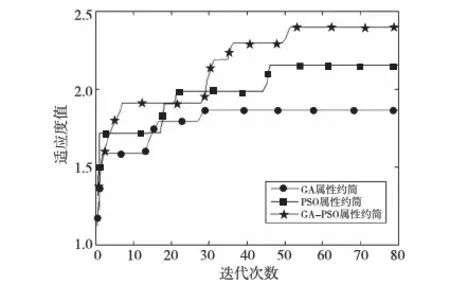
Figure 1 Fitness value curve of Zoo evolution图1 Zoo进化过程适应度值变化曲线

Figure 2 Numbers of experiments vs run time about Zoo reduction图2 Zoo约简实验不同次数运行时间曲线

由实验结果可以看出，GA-PSO约简算法与遗传算法相比，运行时间短且能得到最小相对属性集；与粒子群算法相比，虽然运行时间相对较长，但是，其约简是以牺牲时间为代价获得最小相对属性集，进而证实本文提出的算法是有效的。本算法在保证运行速度相对快的前提下，能得到最小相对属性集。

5 结束语

近年来粗糙集理论以其独特的优势引起了广泛的关注，并成功应用于临床医疗诊断、量子粒子群[7]、预测控制、机器学习和数据挖掘[8]等诸多领域。粗糙集理论与人工智能算法相结合也是其应用范围之一。但是，粗糙集理论中求解最小约简是NP-hard 问题。本文提出了一种基于GA-PSO的粗糙集属性约简算法，在跨越局部搜索障碍的同时又保证了最小相对属性约简。实验表明，该算法在决策表属性约简中的有效性和实用性。本算法虽然求得了最小相对属性约简集，但是以牺牲时间为代价，如何高效地对决策表进行属性约简是今后进一步研究的方向。

[1] Pawak Z.Rough sets[J].International Journal of Computer and Information Science,1982,11(5):314-356.

[2] Dai Jian-hua,Li Yuan-xiang.An algorithm for reduction of attributes in decision system based on rough set[J].Mini-Micro System,2003,3(3):523-526.(in Chinese)

[3] Xiao Hou-guo,Sang Lin.Rough set attribute reduction algorithm based on GA and its application[J].Computer Engineering and Applications,2008,44(15):228-230.(in Chinese)

[4] Walczak W,Massart D L.Tutorial,rough sets theory[J].Chemo Metrics and Intelligent Laboratory Systems,1999,47:1-16.

[5] Yan Yan,Yang Hui-zhong. Rough set attribute reduction algorithm based on GA [J].Computer Engineering and Applications,2007,43(31):156-158.(in Chinese)

[6] Dai Jian-hua,Chen Wei-dong,Gu Hong-ying,et al.Particle swarm algorithm for minimal attribute reduction of decision data tables[C]∥Proc of Multi-Symposiums on Computer and Computational Sciences,2006:572-575.

[7] Wang Jia-yang,Xie Ying.Minimal attribute reduction algorithm based on quantum particle swarm optimization[J].Computer Engineering,2009,35(12):148-150.(in Chinese)

[8] Huang Xiao-fang.Algorithm of decision tree in data mining and its application[J].O.I.Automation,2005,24(2):35-36.(in Chinese)

附中文参考文献：

[2] 代建华,李元香.一种基于粗糙集的决策系统属性约简算法[J].小型微型计算机系统,2003,3(3):523-526.

[3] 肖厚国,桑琳.基于遗传算法的粗糙集属性约简及其应用[J].计算机工程与应用,2008,44(15):228-230.

[5] 颜艳,杨慧中.基于遗传算法的粗糙集属性约简算法[J].计算机工程与应用,2007,43(31):156-158.

[7] 王加阳,谢颖.基于量子粒子群优化的最小属性约简算法[J].计算机工程,2009,35(12):148-150.

[8] 黄晓芳.数据挖掘中决策树算法及其应用[J].兵工自动化,2005,24(2):35-36.