也谈多频率激励下稳态电路的最大功率传输问题

孙 盾,田社平,范承志

(1.浙江大学电气工程学院,浙江杭州 310027;2.上海交通大学电子信息与电气工程学院,上海 200240)

也谈多频率激励下稳态电路的最大功率传输问题

孙 盾1,田社平2,范承志1

(1.浙江大学电气工程学院,浙江杭州 310027;2.上海交通大学电子信息与电气工程学院,上海 200240)

正弦稳态电路最大功率传输问题是电路理论课程的重要教学内容。该文以包含2个正弦激励的非正弦周期稳态电路为例,讨论多频率激励下稳态电路最大功率传输问题。非正弦周期稳态电路平均功率等于直流分量和各次谐波分量分别产生的平均功率之和,因此,非正弦周期稳态电路的负载所获得的功率至多等于电源各谐波分量单独作用时负载所获得的最大功率之和。

最大功率传输;多频率激励;稳态电路

[1]《多频率电源下的最大功率传输问题研究》一文(以下简称“研究文章”),讨论了多频率激励作用情况下稳态电路的最大功率传输问题,但该文所附测量结果(见“研究文章”中表1和表2)有明显差错。诚然,最大功率传输是电能及信号传输中必须考虑的重要问题,也是“电路理论”教学的重点内容[2-4]。对于正弦稳态电路,在负载阻抗可以无约束调节的情况下,可以通过调节负载阻抗与正弦电源的内阻抗(或含源线性一端口网络的输出阻抗)达到共轭匹配,实现负载从电源获得最大平均功率的要求,当实际应用中的负载阻抗不可调节时,需要通过阻抗变换的方式来实现前述的共轭匹配条件[5-8]。当激励源为多频率分量时,在什么条件下,负载可以获得最大功率,是一个值得探讨的问题。多频率激励同时作用情况下,即便负载可以自由变化,负载获得最大功率条件的解析表达式很难推导出来,更不用说负载固定需要通过双口网络变换阻抗的情况了。

下面针对“研究文章”中存在的问题作一讨论。希望通过讨论切磋,引发大家共同思考。

1 激励含两种频率分量f1＝0.159 Hz、f2＝0.318 Hz且负载为阻抗

“研究文章”经过分析,得出如下结论:如果负载阻抗同时满足ZL(j1)＝(0.5－j0.5)Ω和ZL(j2)＝(0.8－j0.4)Ω,则负载将得到最大功率Pmax＝31.25 W。对于图1电路,由于负载的拓扑规定为RC串联网络,一

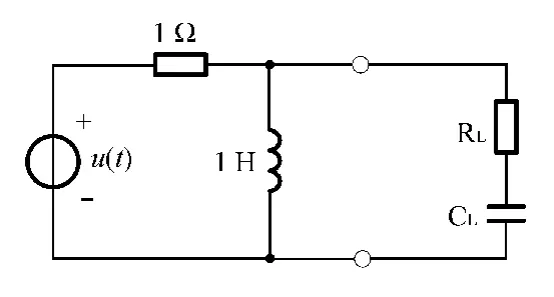
图1 负载为RC串联阻抗的情况

图1所示负载为可变阻抗的非正弦周期稳态电路(见“研究文章”图2),其激励为般来说,该网络并不满足上述结论中的条件,因而RC串联负载不可能获得最大功率。但是,在“研究文章”中表1中的12组测量数据中,居然有6组测量数据的最大功率超过31.25 W,这显然是不可能的。

通过仿真分析发现,由于激励的频率很低,实际上功率表的读数是不稳定的。我们利用PSPCIE仿真,仿真电路及仿真波形如图2所示。从图2可以发现,从第4秒开始(进入稳态),负载瞬时功率在约3～47 W之间呈周期变化。既然瞬时功率按周期性变化,其平均值应该是稳定的。仿真中瓦特表读数不稳定的原因是由仿真软件的算法所决定的。一般来说,仿真软件的平均值算法是基于当前数据的总体平均,因此随着仿真的进行,新的数据不断加入,造成结果不断波动。只要调小仿真步长,那么功率表的读数大概在13 W左右波动,而不会超过14 W(见图3)。实际上电阻RL在0.5～0.8Ω,容抗XC在0.5～0.4Ω而不是电容C在0.5～0.4Ω之间变化,所以图3所示负载获得功率远没有到达最大功率31.25 W,而是在13 W左右徘徊。

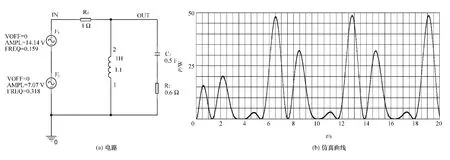
图2 RL＝0.6Ω,CL＝0.5 F时R2吸收的瞬时功率Pspice仿真结果

图3 RL＝0.6Ω,CL＝0.5F时R2吸收的平均功率Multisim仿真结果

2 激励含两种频率分量f1＝159 Hz、f2＝318 Hz且负载为阻抗

为了避开平均功率仿真数据的不稳定因素,下面的讨论将把多频率激励的基波和谐波频率提高为原来的1 000倍。

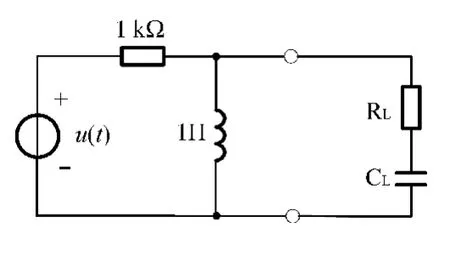
图4 频率分量f1＝159 Hz、f2＝318 Hz时电路

类似地,当电源谐波分量u2(t)＝52cos(2 000t)单独作用时,电源的等效阻抗及开路电压相量经计算分别为

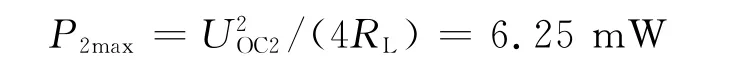
因此,负载可以得到的最大功率为P＝P1max＋P2max＝31.25 m W。

为了便于与“研究文章”比较,参照同样的分析方法,当电阻RL在500～800Ω、容抗XC在500～400Ω、电容C在2～1.25μF之间变化时,选择若干取值,利用Multisim仿真,得到负载获得平均功率的读数列于表1当中,仿真图如图5所示。

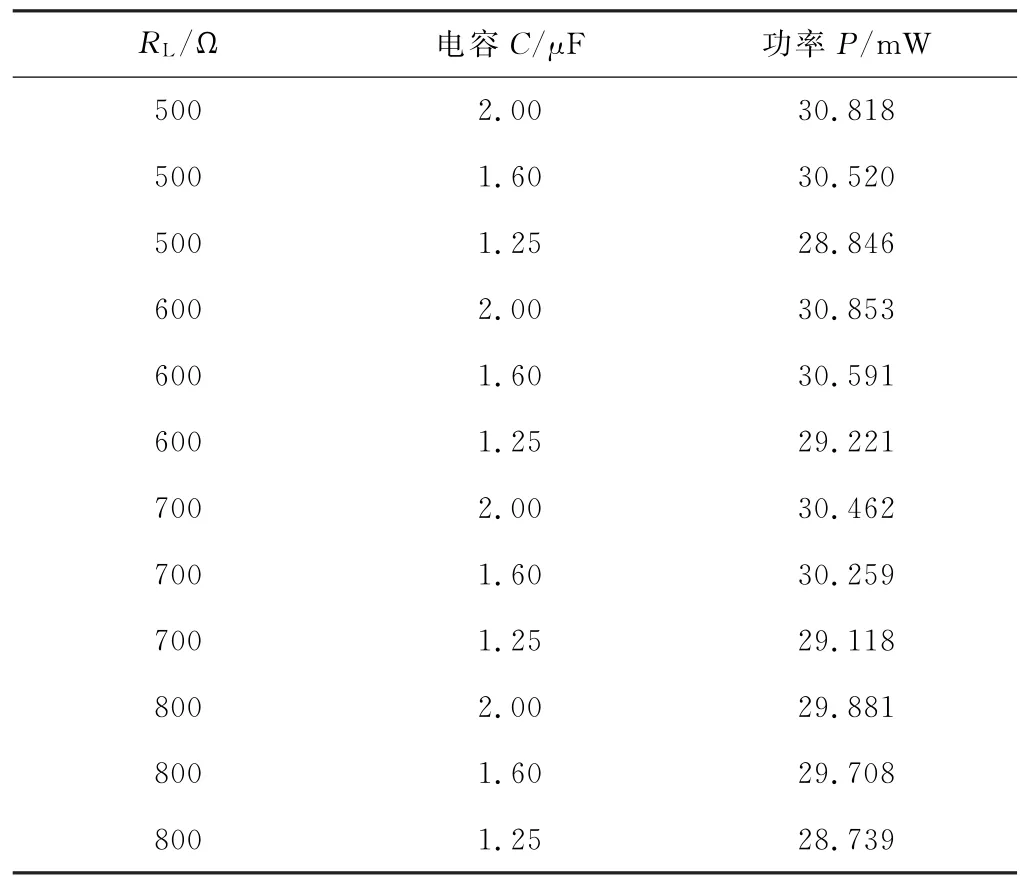
表1 不同容性负载取值时对应的功率

从表中数据可以清晰看出,负载上所获得的功率不会超过分别获得的最大功率之和,即31.25 m W。

图5 RC变化时负载获得功率的Multisim仿真结果

3 激励含两种频率分量f1＝159 Hz、f2＝318 Hz且负载为电阻

针对图4所示电路,但负载只能是纯电阻(去掉CL)。利用叠加定理,仅当u1(t)＝10cos(1 000t)单独作用时,电源的等效阻抗及开路电压相量分别为

类似地,当电源谐波分量u2(t)＝5 2cos(2 000t)单独作用时,电源的等效阻抗及开路电压相量分别为

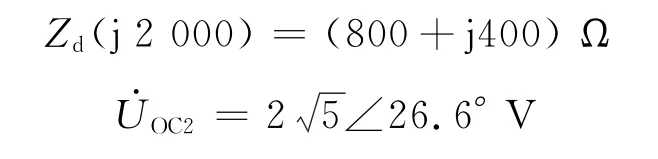
当电阻RL在500～400Ω之间变化时,选择若干取值,利用Multisim仿真,得到负载获得的平均功率的读数见表2。

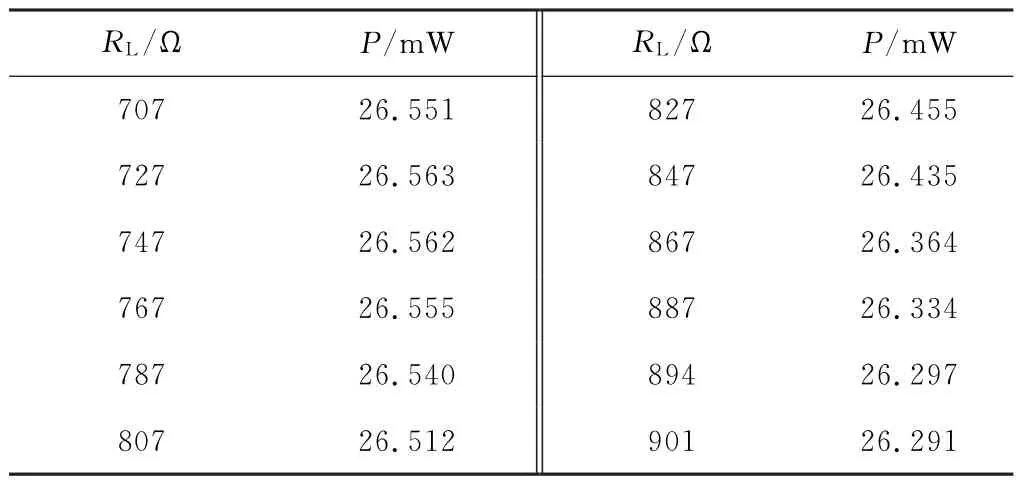
表2 不同阻抗负载取值时对应的功率

从表2中数据可以清晰看出,负载上所获得的功率也没有超过分别获得的最大功率之和,即26.61 m W,当然肯定小于负载为阻抗情形下的31.25 mW。

4 进一步的讨论

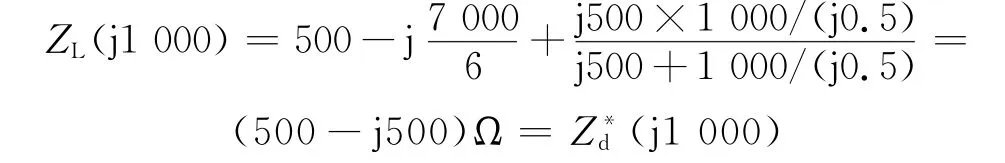
而当ω＝2 000 rad/s时,支路ad发生并联谐振,负载阻抗为

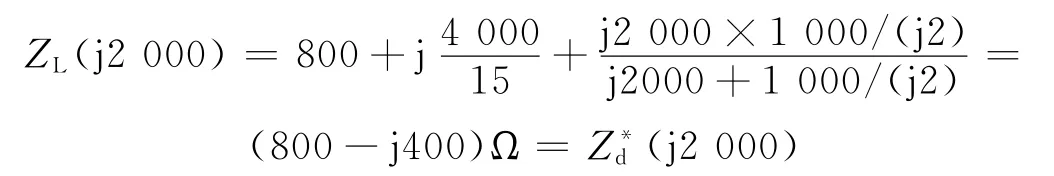
因此,图6所示电路能够获得最大功率Pmax＝31.25 m W,Multisim仿真结果与上述分析完全吻合。

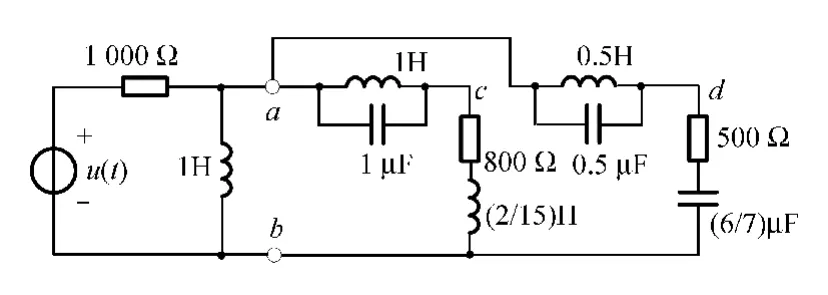
图6 阻抗负载获得最大功率的电路

5 结论

在多频率激励下,负载获取最大功率条件的解析表达式很难推导,其本质上是一个负载所获得功率表达式的数学求极值问题。由最大功率传输定理可知,单一频率而且当负载阻抗与电源等效阻抗互为共轭复数时,负载获得最大功率;单一频率而且当电阻负载与电源等效阻抗的模匹配时,负载获得最大功率;对非正弦周期稳态电路,其平均功率等于直流分量和各次谐波分量分别产生的平均功率之和,因此,非正弦周期稳态电路的负载所获得的功率至多等于电源各谐波分量单独作用时负载所获得的最大功率之和。

本文通过例子讨论了非正弦稳态周期电路最大功率传输问题,限于篇幅,电源仅包含2个谐波分量。对于含有多个谐波分量电源激励的情况,可作类似分析。本文的教学理念[10-12]讨论可供从事电路理论教学的教师参考。

参考文献(References)

[1]曹倩玉,刘子溪,范诗溪,等.多频率电源下的最大功率传输问题[J].实验技术与管理,2014,31(5):58-60.

[2]Charles K.Alexander,Matthew N.Sadiku.Fundamentalsof Electric Circuits[M].北京:清华大学出版社,2000.

[3]陈洪亮,张峰,田社平.电路基础[M].北京:高等教育出版社,2007.

[4]范承志,孙盾,童梅.电路原理[M].北京:机械工业出版社,2009.

[5]刘秀成,黄松岭,于歆杰,等.关于最大功率传输问题的讨论[J].电气电子教学学报,2008,30(1):19-22.

[6]田社平,陈洪亮.关于正弦稳态功率传输的讨论[J].电气电子教学学报,2008,30(6):7-9.

[7]颜秋容.实现最大功率传输的阻抗变换方法研究[J].电气电子教学学报,2011,33(3):40-44.

[8]颜秋容,李妍,曹娟,等.最大功率传输定理应用的思考[J].电气电子教学学报,2007,29(3):51-53.

[9]王鹏.正弦稳态下最大功率传输探讨[J].阜阳师范学院学报:自然科学版,2006,2008,23(4):8-9,20.

[10]高原,王土央.本科生创新能力培养体系的探索与实践[J].实验技术与管理,2011,28(6):30-32.

[11]董健,郭迎.以大学生创新性实验推动本科生培养模式改革[J].实验技术与管理,2013,30(8):183-186.

[12]赵学凯.基于学生学习主体地位的实验教学方法改革研究[J].实验技术与管理,2010,27(2):17-20.

更 正

本刊2015年第1期第75页汪涛老师原论文中没有通信作者,是编辑过程中误加,应去掉。

《实验技术与管理》杂志编辑部 2015年第3月20日

On maximum power transfer of steady-state circuits under multi-frequency excitation

Sun Dun1,Tian Sheping2,Fan Chengzhi1
(1.College of Electrical Engineering,Zhejiang University,Hangzhou 310027,China; 2.School of Electronic,Information and Electrical Engineering,Shanghai Jiaotong University,Shanghai 200240,China)

It is an important lecture about the maximum power transfer in sinusoidal steady-state circuit.Taking two non-sinusoidal periodic steady-state circuits with sinusoidal excitation as an example,this paper has discussed the maximum power transfer problems.The conclusion is drawn that the maximum power of the non-sinusoidal periodic steady-state circuit is not greater than the sum of the corresponding maximum powers of the respective sinusoidal steady-state circuits.

maximum power transfer;multi-frequency excitation;steady-state circuit

TM133

A

1002-4956(2015)4-0062-04

2014-08-06

浙江省2013高等教育教学改革项目“电类系列课程体系结构建设与教学实践”(jg201311);国家级电类基础课程教学团队建设项目(教育部,2010);2013浙江大学本科大类课程建设项目“电路与模拟电子技术”课程建设

孙盾(1966—),女,江西南昌,硕士,副教授,主要从事电工理论的教学与研究工作.

E-mail:sundun01＠163.com