基于基尼系数的区域创新投入产出熵权TOPSIS匹配性评价分析
贾颖颖, 郭 鹏, 赵 静
(西北工业大学 管理学院,陕西 西安 710072)
基于基尼系数的区域创新投入产出熵权TOPSIS匹配性评价分析
贾颖颖, 郭 鹏, 赵 静
(西北工业大学 管理学院,陕西 西安 710072)
采用匹配基尼系数对我国创新系统投入产出匹配性程度进行了测算。通过构建基于基尼系数的TOPSIS熵权评价模型,对我国大陆31个省市自治区的创新投入产出匹配性进行了评价,对各地区投入产出匹配性评价值聚类分析。研究结果表明我国创新系统投入产出呈现出不匹配的状态,形成了京津、长江三角洲和珠江三角洲三个极化区域。研究结果验证了本文构建模型的可行性和合理性,为区域创新投入产出的研究提供了新的思路。
区域创新;投入产出;匹配性;基尼系数;熵权TOPSIS
0 引言
在知识经济发展和经济全球化过程中,随着区域的不断发展和竞争的日益加剧,区域创新能力已成为一个地区经济是否拥有国际竞争优势的决定性因素,是建设和增强区域竞争能力的关键和核心。党的“十七大”将提高区域创新能力作为国家发展战略的核心。“十八大”政府工作报告中也提出科技创新是提高社会生产力和综合国力的战略支撑,必须摆在国家发展全局的核心位置。以建设创新型国家为目标,我国对科技创新活动的投入力度持续增加,研发活动经费投入从2006年开始已经超过日本,仅次于美国。研发经费投入占GDP的比重已由2000年的0.9%增加到2010年的1.77%,但这一指标相比于发达国家仍存在较大差距。在科技创新活动有效性产出方面,我国也远远落后于传统创新型国家以及新型工业发达国家。
我国地区辽阔,区域之间发展不均衡,区域创新资源投入和产出表现出明显的差异,有些地区存在投入与产出不匹配的情况。1998~2007年间陕西年均研发经费是福建的1.8倍,但年均专利产出却不足后者的30%。在我国科技创新资源严重不足,区域创新能力发展不均衡的情况下,则更需要最大限度地利用资源,避免“高投入,低产出”现象的发生,提高资源投入产出的匹配性。然而,这种“匹配性”并没有通过数量化研究体现出来。因此,研究区域创新系统的投入产出匹配性,对我国整体以及各地区区域创新投入产出匹配程度有定量化的认识,就显得尤为必要。
目前,对区域创新投入产出和资源配置领域的研究热点为投入产出转化率即创新效率。众多学者通过SFA、DEA模型、Malmquist指数等测算区域创新效率进行区域创新资源配置的研究[1~5]。匹配性这一概念在其他领域已有相关研究成果[6,7],但在区域创新投入产出领域并没有形成系统的研究结论,没有从投入产出匹配性角度进行定量化研究。本文在区域创新投入产出中引入匹配性这一概念,将基尼系数和熵权TOPSIS两种方法相结合,在分析我国整体区域创新系统的投入产出匹配性的基础上,对我国大陆31个省市自治区的区域创新系统投入产出进行匹配性评价,为针对性改善我国区域间创新资源投入结构,合理利用创新资源提供理论依据和政策参考。为区域创新系统投入产出研究提供新的思路。
1 模型、指标和数据
1.1 指标选择与数据来源
区域创新系统的投入应反映区域通过自身生产或者购买系统外部技术等方式改善技术的能力[8]。由于通过自主创新或者购买域外技术都需要人力和财力资源作为投入,因此之前大量研究者都将区域创新系统的资源投入分为财力和人力资源投入两类[1,9]。本文也采用这种方法,将区域创新系统投入分为财力资源投入和人力资源投入。同时,为了消除投入产出规模的影响,有利于投入与产出强度的匹配性分析,本文选取相对指标值作为区域创新系统的投入产出指标[10]。综合于晓宇[1]、樊华[4]等研究,本文设计的区域创新系统人力资源投入指标有:科技人员占就业人口比重(X1),研发人员占科技人员比重(X2)以及科学家和工程师占研发人员比重(X3)。财力资源投入指标有:科技经费支出占GDP比重(X4),R&D经费占GDP的比重(X5)和地方科技财政拨款占地方财政支出的比重(X6)。在区域创新系统的产出指标上,考虑到专利能够反映一个国家或地区的创新资源投入转化为产出的最核心和最富经济价值的部分,能够反映科技成果的创新能力[11,12]。在我国,专利包括发明、实用新型和外观设计三种形式。三种专利中,发明专利是衡量创新产出水平的较好指标,其技术含量高且申请量很少受到专利授权机构审查能力的约束,更能客观地反映出一个地区原始创新能力与科技综合实力[13~15]。因此本文选取每万人发明专利申请授权数(Y1)来衡量区域创新系统产出。研究数据主要来源于《中国统计年鉴》、《中国科技统计年鉴》和《第二次全国R&D资源清查资料汇编》。《中国科技统计年鉴》从2009年开始就没有收录科技人员和科技经费投入这两项指标的统计数据,因此本文所使用的创新系统投入基础数据来源于2008年,由于从创新资源的投入到产出有一定的时间延时,本文综合考虑俞立平[16]、陈伟[17]的方法,将滞后期设为2年。区域创新系统产出的基础数据来源于2010年。本文研究对象为中国内地的31个省级行政地区。
1.2 模型
各地区创新系统投入产出匹配性评价需要通过计算其对应的投入指标在洛伦兹曲线中的斜率得出,因此各地区的创新系统投入产出匹配程度的计算包括两个阶段。第一阶段引入基尼系数的算法,绘制基于创新成果产出的各创新投入指标的洛伦兹曲线,用于我国区域创新系统投入产出匹配基尼系数的计算,反映我国创新资源投入产出的匹配程度。第二阶段,计算各地区创新系统投入产出匹配程度。为了界定各个区域创新投入产出匹配状况与理想状态的贴近度,计算各地区投入产出匹配程度的相对值而非绝对值,本文采用熵权TOPSIS方法进行各地区创新系统投入产出匹配性评价。TOPSIS是一种双基点比较法,通过与最理想和最不理想的虚拟对象进行比较,得到各评价对象的评价值[18]。传统 TOPSIS 法测算待评价方案时,其指标权重为事先给定的,这在一定程度上存在主观性[19]。熵权是一种客观赋权法,能非常好的利用权重反映指标值间的分布差异。为剔除主观性的影响,本文考虑利用熵权法对待评价方案的相关指标进行赋权,从而实现对区域创新系统投入产出匹配性的客观评价。
1.2.1 匹配基尼系数
基尼系数作为一种有效的变量均衡分析的统计工具,在经济领域中的应用十分广泛。基尼系数不仅仅被用于收入分配问题的研究,它还可用于财产、资本、市场和资源分配等一切均衡程度的分析。因此,它也被称为广义均衡分析的工具。匹配基尼系数作为一种衡量匹配程度的方法已被广泛应用于资源匹配性和资源分配等研究中[20~23]。在我国,区域创新资源投入呈现非均衡性特征,这也直接关系到区域经济发展和区域创新能力的提升,其内涵的数学规律类似于基尼系数所表达的收入分配的均衡问题。因此,区域创新系统资源投入的非均衡程度及其与创新产出的匹配程度,用洛伦兹曲线和基尼系数描述,具有很好的一致性。
根据基尼系数的内涵,将其引入到创新系统资源投入和创新产出的匹配性中,可以作如下假设:基于投入一定比例的创新资源,如果回报相同比例的创新产出,则创新系统的投入产出为绝对匹配。
区域创新投入产出匹配基尼系数的具体思路是以各地区发明专利授权数累计百分比为纵坐标[10],以选取的各个创新系统投入指标累计百分比为横坐标。用各地区累计发明授权数除以横坐标所指向的指标,以所得商作为特征值,将特征值按照从低到高的顺序依次排列,绘制各个投入指标基于发明专利授权量这个产出指标的洛伦兹曲线,并以此求基于产出指标的各个投入指标的匹配基尼系数。
基尼系数的计算方法有很多种[24],本文选用梯形面积法进行基尼系数的计算:
(1)
其中,Xi为第i个地区创新投入各指标的累积百分比。Yi为发明专利授权数累积百分比。当i=1时,(Xi-1,Yi-1)视为(0,0)。
投入产出匹配基尼系数内涵与一般的基尼系数内涵相似,因此本文对匹配基尼系数的划分标准采用基尼系数的国际惯例。基尼系数低于0.2表示投入产出高度匹配;0.2-0.3表示比较匹配;0.3-0.4表示相对匹配;0.4-0.5表示投入产出不匹配;0.5以上则表示非常不匹配。
1.2.2 熵权TOPSIS
由于每个区域在每一指标洛伦兹曲线的斜率代表了其相对于该指标的发明专利产出比值[20]。因此,本文以其在每个曲线上的斜率代表其在该指标下的值。通过熵权法确定基于发明专利授权量的各投入指标的权重,熵权法是通过指标数据的变化大小确定指标权重的客观赋权法。在确定权重后,通过TOPSIS方法,即逼近理想解的方法,确定被评价对象的排序。
(1)利用熵权法计算6个指标的权重[26]
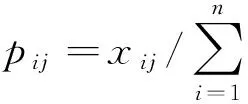

③计算指标xj的差异系数。定义差异系数gj=1-ej,gj越大,越应重视该指标的作用;
(2)构建加权决策矩阵
①形成决策矩阵。设参与匹配性评价的地区集合为M=M1,M2,…,Mm,其包含的指标集为D=D1,D2,…,Dn,则Mi对指标Dj的值记为xij(i=1,2,…,m;j=1,2,…,n),则决策矩阵为:
②构建加权决策矩阵。将各指标权重wj与无量纲化矩阵*由于本文进行匹配性评价中各指标的值为洛伦兹曲线中相对应的斜率,已消除量纲差异,所以本文中无需进行标准化。X相乘,得到加权决策矩阵R=(rij)m×n,其中rij=wj×xij。
(3)计算正、负理想解
利用上述加权决策矩阵计算正、负理想解的公式[19](4)和(5)

(4)计算评价对象与理想解的欧氏距离

(5)计算相对贴近度计算评价结果
按照相对贴近度确定各个地区创新系统投入产出匹配状况,相对贴近度ci越大表示被评价地区与正理想解越相近,投入产出越匹配。相对贴近度ci的大小顺序即为各个地区创新系统投入产出匹配程度的优劣排序。
2 我国区域创新系统的投入产出匹配性评价结果分析
2.1 区域创新系统投入产出匹配基尼系数计算
根据匹配基尼系数的计算方法,首先分别绘制基于各区域创新系统投入指标的发明专利产出洛伦兹曲线。如图1至图6所示。

图1 基于科技人员投入的洛伦兹曲线
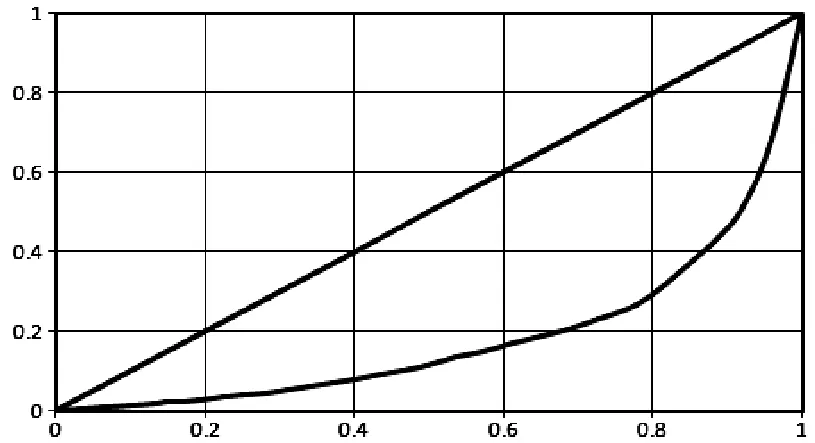
图2 基于研发人员投入的洛伦兹曲线

图3 基于科学家和工程师投入的洛伦兹曲线
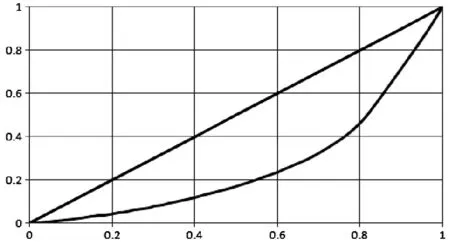
图4 基于科技经费投入的洛伦兹曲线

图5 基于研发经费的洛伦兹曲线

图6 基于地方财政支出的洛伦兹曲线
由洛伦兹曲线可以看出,我国区域创新系统人力资源投入和财力资源投入与创新产出均呈现不完全匹配的状态,同时各投入指标与产出之间的匹配程度也存在明显差异。基于这几项指标匹配性的数值可以由公式(1)计算得出,具体结果如表1所示。

表1 各指标匹配基尼系数值
根据匹配基尼系数的划分标准,除了基于科技人员投入(X1)这项指标的基尼系数处于相对匹配状态,其余五项指标的匹配基尼系数处于不匹配状态,同时基于研发人员投入(X2)和科学家、工程师投入(X3)这两项指标的基尼系数均处在非常不匹配的范围。这说明,无论是人力资源还是财力资源,我国区域创新系统的投入产出基本呈现出较差的匹配性。
2.2 各地区区域创新系统投入产出匹配性评价
在通过匹配基尼系数确定各投入指标的洛伦兹曲线后,计算每个区域在各指标对应洛伦兹曲线的斜率,即为各指标的得分。运用熵权TOPSIS方法进行评价,即可得到各地区创新系统投入产出匹配性评价值。
根据各指标的数值,首先采用熵权法计算各指标的权重,获取各指标的加权得分。然后运用TOPSIS法对人力资源和财力资源投入各指标进行匹配性评价,计算出基于人力资源投入的区域创新产出匹配性得分、基于财力资源投入的区域创新产出匹配性得分以及各地区创新系统投入产出匹配性综合得分。匹配性综合得分的高低比较可以理解为:当投入相同比例的资源时,得分较高地区所获得的产出要高于得分较低地区获得的产出。即得分越高,说明该地区投入产出越匹配,反之,则说明该地区投入产出匹配性低。各地区匹配性得分及排名如表2所示。
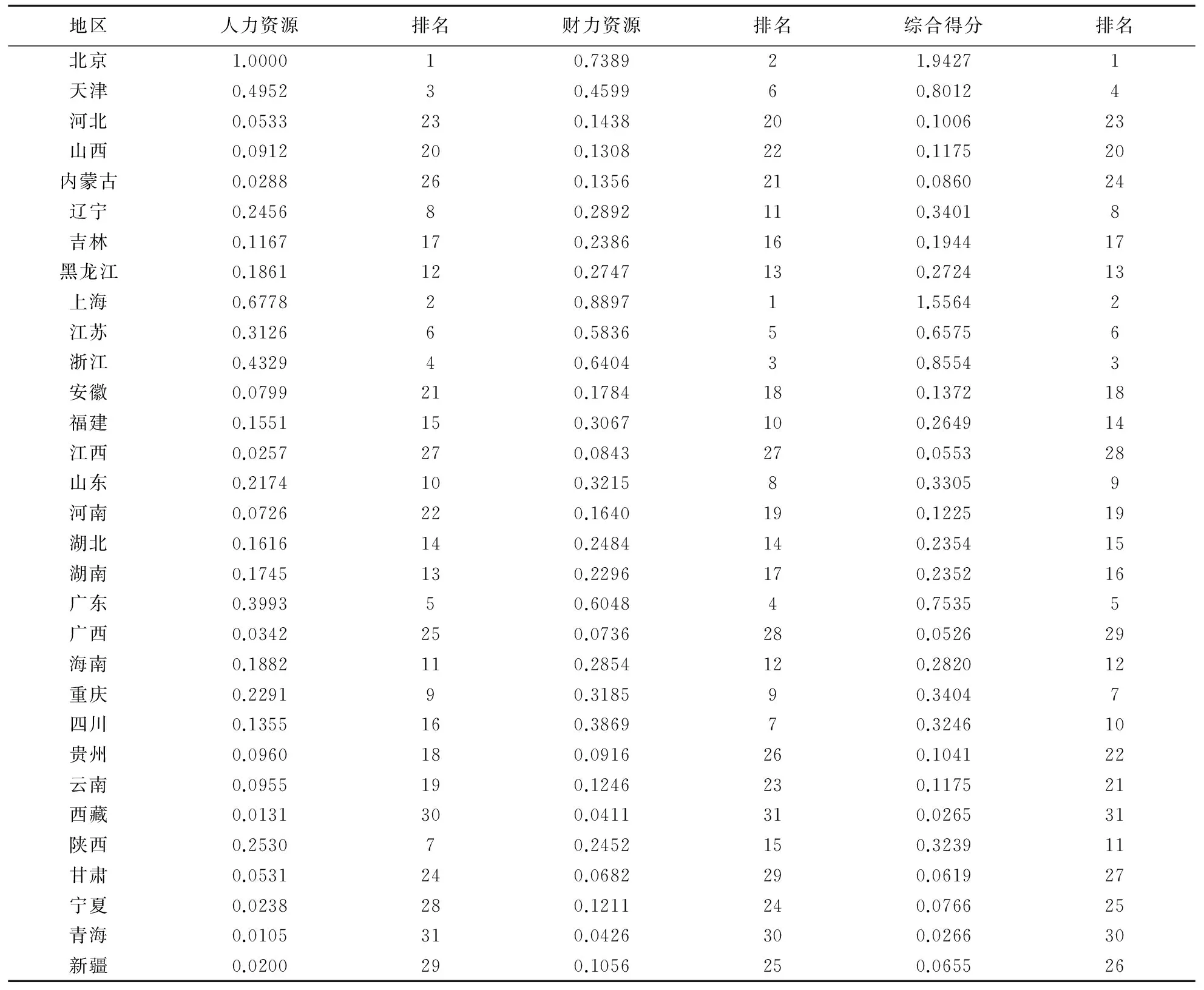
表2 各地区匹配性得分及排名
基于人力资源投入的创新产出匹配性得分排名前6的地区依次为:北京、上海、天津、浙江、广东和江苏,全部为东部地区*按经济区划,我国分为东部地区、中部地区和西部地区,东部地区包括北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东和海南共11个省市;中部地区包括山西、吉林、黑龙江、安徽、江西、河南、湖北、湖南8个省;西部地区包括重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆、广西、内蒙古、西藏等12个省市、自治区。。这6个地区也是基于财力资源投入的创新产出匹配性得分以及综合得分的前6名(名次不同)。在匹配性综合得分排名前10的省市中,东部地区8个,西部地区2个分别为重庆和四川。在匹配性得分排在后面的10个省市中,东部地区1个,中部地区1个,西部地区则有8个。考虑到西部大部分地区是经济发展落后地区,创新资源匮乏,创新能力较低,属于低投入带来的是更低的产出,说明西部地区整体的投入产出匹配性较低。
2.3 聚类分析
为了更好地对我国各地区区域创新投入产出匹配性的分级特征进行研究,本文将我国31个省市自治区的匹配性得分进行聚类分析。根据指标特征,本文选择中间距离法(Dendrogram Using Median Method)作聚类分析的具体方法,形成聚类树状族谱,结果如图7所示。

图7 我国各省域区域创新系统投入产出匹配性聚类分析谱系图
根据聚类分析结果,本文将我国各地区创新系统投入产出匹配性分为三个层次:1.0~2.0表示投入产出匹配,0.5~1.0表示投入产出基本匹配,0~0.5表示投入产出不匹配。
第一层次为北京、上海。首都北京和国际化大都市上海由于其独特优势和经济环境,拥有良好的科技和教育资源,汇集了大量优秀的科技创新人才和创新资金的投入,高投入带来了高产出。北京在基于人力资源投入的匹配性得分位列第一,上海在基于财力资源投入的匹配性得分居于全国各地区首位,说明这两个地区创新系统的投入产出匹配性处于全国领先位置,创新系统的投入和产出匹配。
第二层次为天津、广东、浙江和江苏。这四个地区地理位置优越,“珠江三角洲”、“长江三角洲”、“环渤海京津冀”经济圈是我国改革开放的先行地区,是我国重要的经济发展区域。浙江、江苏、广东和天津这四个地区得益于三大经济圈的高速发展,有较好的创新环境和创新能力[26]。这四个地区基于人力资源和财力资源的匹配性得分都位于全国前六名之中,说明这四个地区创新系统的投入产出基本匹配。
第三层次为吉林、海南、福建、黑龙江、湖南、湖北、山东、陕西、四川、辽宁、重庆、甘肃、新疆、广西、江西、宁夏、内蒙古、西藏、青海、安徽、河北、贵州、河南、云南和陕西。福建、湖南、湖北、河北、山东、黑龙江、吉林和辽宁等地区有较好的经济基础,创新资源投入的力度也较大,由于创新环境和创新意识薄弱等问题,这些地区属于“高投入,低产出”。西部地区的12个省市自治区全都归于第三层次。西部地区属于经济欠发达地区,创新基础薄弱,政策支持力度较小,较低的创新资源投入回报的是更低的产出。这些地区的创新系统投入产出不匹配。
3 结论
本文通过匹配基尼系数,对2010年我国整体以及各地区的创新投入产出匹配性进行测算,无论是人力资源还是财力资源,我国整体创新资源投入产出都非常不匹配。通过构建基于基尼系数的创新系统投入产出匹配性评价模型,对2010年我国各地区创新投入产出的匹配性进行了定量化研究,得到每个地区的匹配性得分,匹配性综合得分排名前6的省市为北京、上海、浙江、江苏、天津和广东。在匹配性得分排在后面的10个省市中,西部地区有8个。通过对各地区匹配性得分进行聚类分析,将我国大陆31个省市、自治区划分为三个层次。北京、上海为第一层次,浙江、江苏、广东和天津为第二层次,其余地区都属于第三层次。匹配性评价和聚类分析结果表明,我国31个地区创新系统投入产出匹配性基本形成长江三角洲、珠江三角洲和京津地区三个极化区域,这也基本反映了我国区域创新投入产出和创新能力的现状,说明本文构建的基于基尼系数的熵权TOPSIS模型有一定的科学性和可操作性。我国整体处于投入产出不匹配状态,西部地区尤为严重。如何有效的进行资源配置,提升地区吸收能力,避免“高投入,低产出”的现象,是今后区域创新系统研究的重点。
[1] 于晓宇,谢富纪.基于DEA-Tobit的区域创新系统资源配置优化策略研究[J].研究与发展管理,2011,(1):1-10.
[2] 白俊红,江可申,李婧.应用随机前沿模型评测中国区域研发创新效率[J].管理世界,2009,(10):51- 61.
[3] 冯锋,张雷勇,高牟等.两阶段链视角下科技投入产出链效率研究——来自我国 29 个省市数据的实证[J].科学学与科学技术管理,2011,32(8):33-38.
[4] 樊华,周德群.中国省域科技创新效率演化及其影响因素研究[J].科研管理,2012,33(1).
[5] 王锐淇,彭良涛,蒋宁.基于SFA与Malmquist方法的区域技术创新效率测度与影响因素分析[J].科学学与科学技术管理,2010,9:121-128.
[6] 张正华,杨先明.西部地区与跨国公司产业投资战略匹配性分析[J].中国软科学,2007,(8):100-109.
[7] 唐晓华,唐要家,苏梅梅.技术创新的资源与激励的不匹配性及其治理[J].中国工业经济,2004,(11):25-31.
[8] Nasierowski W, Arcelus F J. On the efficiency of national innovation systems[J]. Socio-Economic Planning Sciences, 2003, 37(3): 215-234.
[9] 刘顺忠,官建成.区域创新系统创新绩效的评价[J].中国管理科学,2002,10(1):75-78.
[10] 樊华,周德群.中国省域科技创新效率演化及其影响因素研究[J].科研管理,2012(01):10-18.
[11] 陈向东,王磊.基于专利指标的中国区域创新的俱乐部收敛特征研究[J].中国软科学,2007(10):76- 85.
[12] Acs Z J, Anselin L, Varga A. Patents and innovation counts as measures of regional production of new knowledge[J]. Research policy. 2002, 31(7): 1069-1085.
[13] 白俊红,江可申,李婧.中国地区研发创新的技术效率与技术进步[J].科研管理,2010,31(6):7-18.
[14] 刘凤朝,沈能.基于专利结构视角的中国区域创新能力差异研究[J].管理评论,2006,18(11):43- 47.
[15] 官建成,何颖.基于DEA方法的区域创新系统的评价[J].科学学研究,2005,23(2):265-272.
[16] 俞立平,熊德平,武夷山.中国地区科技效率的组合测度研究[J].科学学研究,2011,(8):1141-1146.
[17] 陈伟,冯志军,康鑫等.区域创新系统的协调发展测度与评价研究——基于二象对偶理论的视角[J].科学学研究,2011,(2):306-313.
[18] 刘希宋,喻登科,曹霞.区域知识资源配置结构和谐指数测度分析[J].管理评论,2011,23(11):126-134.
[19] 买生,匡海波,张笑楠.基于科学发展观的企业社会责任评价模型及实证[J].科研管理,2012,33(3).
[20] 邱俊永,钟定胜,俞俏翠等.基于基尼系数法的全球CO_2排放公平性分析[J].中国软科学,2011,(4):14-21.
[21] 王金南,逯元堂,周劲松.基于 GDP 的中国资源环境基尼系数分析[J].中国环境科学,2006,26(1):111-115.
[22] 鲍文,陈国阶.基于水资源的四川生态安全基尼系数分析[J].中国人口.资源与环境,2008,18(4):35-37.
[23] 吴宇哲,鲍海君.区域基尼系数及其在区域水土资源匹配分析中的应用[J].水土保持学报,2003,17(5):123-125.
[24] 叶礼奇.基尼系数计算方法[J].中国统计,2003,4:58.
[25] 夏勇其,吴祈宗.一种混合型多属性决策问题的TOPSIS方法[J].系统工程学报,2004,19(6):630- 634.
[26] 李刚,迟国泰,程砚秋.基于熵权TOPSIS的人的全面发展评价模型及实证[J].系统工程学报,2011,26(3):400- 407.
[27] 周立,吴玉鸣.中国区域创新能力: 因素分析与聚类研究——兼论区域创新能力综合评价的因素分析替代方法[J].中国软科学,2006,8:96-103.
Entropy Weight and TOPSIS Evaluation on the Matching of the Regional Innovation Input and Output Based on the Gini Index
JIA Ying-ying, GUO Peng, ZHAO Jing
(SchoolofManagement,NorthwesternPolytechnicalUniversity,Xi’an710072,China)
The paper measures the matching level of the regional innovation input and output based on the matching gini index. Then it establishes the entropy weight and TOPSIS evaluation model based on the Gini Index to evaluate the matching level of 31 provincial regions in China. Then we analyze the matching evaluating value of every region in clusfer. The result demonstrates the input and output of China regional innovation are mismatched and form the polarized area, which are the Pearl River Delta, the Yangtze River Delta and the Beijing-Tianjin region. The research results verify the feasibility and rationality of the proposed model. A new and scientific thought is provided to study the regional innovation input and output.
regional innovation; input and output; matching; gini index; entropy weight and TOPSIS
2013-10-15
国家自然科学基金资助项目(71272049);高等学校博士学科点专项科研基金(20126102110052),国家软科学研究计划(2010GXS5D264);西安市软科学研究计划(HJ1108-3)
贾颖颖(1989-),女,陕西西安人,博士研究生。研究方向:区域创新系统,综合评价理论与方法。
F207
A
1007-3221(2015)02- 0208- 07

