基于弹性区带架构的多目标设施布局问题研究

常 征， 吕 靖

(大连海事大学 交通运输管理学院，辽宁 大连 116026)



基于弹性区带架构的多目标设施布局问题研究

常 征， 吕 靖

(大连海事大学 交通运输管理学院，辽宁 大连 116026)

为解决设施面积不等的连续型设施布局问题，建立了基于弹性区带架构布置形式，以物料搬运成本最小、邻近关系最大、距离要求满足度最大的多目标设施布局模型。模型中考虑了区域内的横向、纵向过道，对设施的长宽比进行了限制，使得结果更符合实际情况。为克服传统多目标单一化方法需要人为设置子目标函数权重、主观性过强的缺陷，采用基于带有精英保留策略的非支配排序遗传算法(NSGA Ⅱ)的多目标优化算法求解模型，设计了相应的编码方式、交叉算子、变异算子、罚函数。最后通过某物流园区的实例分析证明了模型与方法的有效性。

工业工程；设施布局；弹性区带架构；不等面积；NSGA Ⅱ；物流园区

0 引言

设施布局问题(Facility Layout Problem, FLP)是指在给定的范围内，对设施的合理安排，以有效地服务于企业的生产运作活动。合理的设施布局设计可以直接影响生产效率，并且减少20%～50%的企业营运成本[1]。FLP最终的解，即布局方案可以有多种表现形式。弹性区带架构(Flexible Bay Structure, FBS)是一种连续型设施布局的表现形式，由Tong在1991年提出[2]。其基本思想是将布局区域分成若干个平行的纵向区带(列)，所有的设施只能放置于各区带中，区带的宽度由其中的设施个数决定。因此，设施布局的问题被简化成为通过确定区带的个数以及每个区带中包含的设施个数，对各个设施进行依次从下往上，从左往右的排列(如图1)。相比其他设施布局表现形式，FBS得到的布局形式较为有限，但是采用FBS布局，可以通过设置一列不放置任何设施的区带，作为布局区域中的过道，方便各个设施之间的物料流动，得出的结果更符合实际情况，也更为实用。因此FBS是最为重要的一种设施布置表现形式。

FLP属于NP问题，传统的方法一般仅适用于设施数小于14个时的布局问题，因此多采用启发式算法进行求解，例如模拟退火算法[3]、禁忌搜索[4]、蚁群算法[5]、粒子群算法[6,7]、人工免疫系统[8]等。经典的FLP的目标函数为最小化物料搬运成本，但是在实际中，决策者需要面对很多互相矛盾的设施布置目标，例如空间利用率、便利性、员工满意度、安全度等[9]，杨薇建立了以物流成本最小和非物流关系最大的双目标设施布置模型[10]，Rosenblatt及Ardestani等以最小化物流成本和最大化邻近关系构建模型[11,12]，曾强等以物料搬运量(或搬运成本)、非物流关系强度、设施所需总面积为优化目标建立多目标优化模型[13]。在多目标优化问题的求解方面，传统的多目标单一化方法，例如最为常见的线性加权法，是通过设定各个子目标函数的权重，将多目标问题转化为单目标问题，但由于权重多通过人为确定，因此该类方法得到的结果过于主观，无法保证多个目标同时得到优化。基于Pareto寻优的方法则是在多目标空间内直接寻优，不需要将多个目标进行转化，因此得到了更为广泛的应用。在该类方法中，多目标遗传算法可以在优化过程中产生一组非劣解，使优化面向Pareto最优解进行，是求解多目标优化问题Pareto最优解的有效手段。常见的多目标遗传算法有向量评估遗传算法(Vector Evaluated Genetic Algorithm, VEGA)[14]、小生境Pareto遗传算法(Niched Pareto Genetic Algorithm, NPGA)[15]、非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm, NSGA)[16]、增强的Pareto最优解进化算法(Strength Pareto Evolutionary Algorithm, SPEA)[17]。其中的NSGA和SPEA的主要思想都是采用合理的种群排序方法，有效地保持了种群的多样性，搜索过程更为有效，方法的应用性也相对较高。Deb在2002年对NSGA进行进一步改进，提出带有精英保留策略的非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm Ⅱ, NSGA Ⅱ)[18]。通过采取基于分级的快速非支配排序法、拥挤度和拥挤度比较算子、精英策略，降低算法的复杂度，保证优化结果的精度，提高了算法的性能。

本文将在前人研究的基础上，建立以物流成本最小、邻近关系最大、距离要求满足程度最高的多目标模型，并设计基于NSGA Ⅱ的多目标遗传算法，解决弹性区带架构下的设施布局问题。

1 模型设计

1.1 问题描述

假设在一个已知范围的矩形平面内要布置若干个设施，出于对搬运物料方便性的考虑，在每一区带之间、以及每一区带包含的各个设施之间都预留出一定宽度的过道。各个设施形状均为矩形且所占面积已知，长度、宽度可在一定范围内浮动。因此设施布置的优化目标为：在满足布置区域总面积限制，设施长宽比限制的条件下，确定可以使设施之间物流成本、邻近关系、距离要求满足度最优化的设施布置顺序。同时模型假设物料的进、出点均在设施的中心点上，且设施与区域边界的距离不予考虑。

1.2 模型构建

(1)参数、变量说明

本文建立的多目标设施布局模型中涉及到的参数、变量定义如下：

m为需要布置的设施个数；A为设施布置区域的总面积；L,H为设施布置区域的长度, 宽度；W为纵向过道的宽度；b为区带的总数目；D为同一区带内设施之间横向过道的宽度；M为较大的常数；α,β为设施长宽比的上限、下限；ai为设施i所占的面积；cij为设施i与设施j之间单位物流量单位距离的搬运费用；dij为设施i与设施j之间的距离；qij为设施i与设施j之间的物流量；nij为设施i与设施j之间的邻近关系；sij为设施i与设施j之间的邻近度因子；rij为设施i与设施j之间的距离要求因子；xi,yi为设施i的坐标值；li,hi为设施i的实际长度和实际宽度；zit为0-1决策变量，当设施i位于区带t时为1，否则为0。

其中，xi,yi,zit是模型的决策变量。

模型的参数变量和参考线如图1。

图1 弹性区带架构下设施布局的参数、变量

(2)目标函数

根据对设施布局问题的假设以及对参数变量的定义，得出本文的多目标设施布局模型：

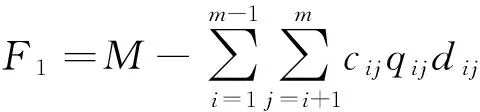
(1)

(2)

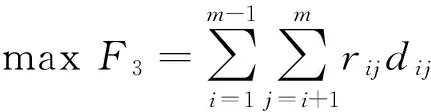
(3)

dij=|xi-xj|+|yi-yj|

(4)

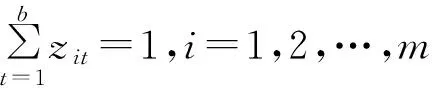
(5)

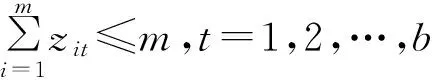
(6)

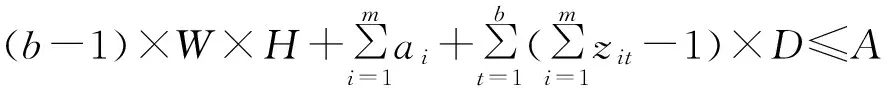
(7)

(8)

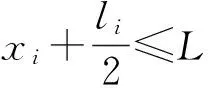
(9)

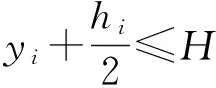
(10)

xi,yi≥0,i=1,2,…,m

(11)

zit=0,i=1,2,…,m,t=1,2,…,b

(12)

邻近关系nij是根据设施之间密切程度等级进行定量化(表1)；邻近度因子sij描述了布局方案中设施的关联程度，其数值由设施之间的距离dij和最大可能距离dmax决定的[19]，定量化方法如表2；距离要求因子rij是由设施之间的环境关系决定的，在一些布局问题中，决策者可能会处于对噪音、污染、环境等会影响员工安全的因素的考虑，要求某些设施之间必须保持一定程度的距离，其数值的定量方法如表3。因此，通过确定各个设施的坐标值，计算设施之间的距离，之后利用距离矩阵，得出邻近度因子矩阵，并结合邻近关系和距离要求因子的数值，则可以计算出三个目标函数值。

式(1)表示最小化物料的总搬运成本，式(2)表示最大化设施之间的邻近关系，式(3)表示最大化地满足对设施之间距离的要求。约束(4)表示设施之间的距离采用Manhattan距离表示；约束(5)表示每个设施只能放在一列上；约束(6)表示每个区带中的设施数不能超过需布置的设施总数；约束(7)表示设施与过道的面积之和不超过可布置的区域的总面积；约束(8)表示设施的长宽之比不超过约束的范围；约束(9)～(10)表示设施不超过可布置区域的范围；约束(11)表示设施布置于车间平面内；约束(12)表示变量的0-1约束。

表1 邻近关系nij对应值表

表2 邻近度因子sij对应值表

表3 距离要求因子rij对应值表

2 基于NSGA Ⅱ算法的求解过程

NSGA Ⅱ算法的基本思想是协调各个子目标函数之间的关系，进而找到使各个子目标都能达到最优的最优解集。NSGA Ⅱ是基于遗传算法建立的，因此仍需要通过遗传算法的交叉、变异等操作产生新一代的个体，差别在于该算法是通过快速非支配排序对种群进行分组，之后通过计算个体的拥挤距离评估每个个体周围的解密度，进而判断同组中个体之间的差异。

根据本文中建立的多目标设施布局模型的特征，首先对NSGA Ⅱ算法中的编码规则，遗传操作等环节进行改进，并设计罚函数。

2.1 编码规则

2.2 遗传操作

(1)交叉。采用部分映射交叉(PMX)处理表示设施排列顺序的第一条整数链：随机选取两个交叉点a1和a2，将两个交叉点之间的中间段进行交换，然后对两个父代中交换区域以外出现的遍历重复，根据交换区域内的位置映射关系，逐一交换，最终得到两个新个体[20]。

(2)变异。采取互换变异方法处理设施排列顺序的整数链的变异操作：随机选取一个变异个体，随机生成[1,m]之间的两个不同整数b1和b2，分别代表第b1个和第b2个设施布置位置，之后交换这两个位置的基因值。采取基于算术变异的方法处理区带内设施数量的整数链的变异操作：随机生成 [m+1,m+b]之间的两个不同整数c1和c2，分别代表第c1和第c2个区带，之后随机变化两个位置的基因值，但是要保持两个基因值的总和不变，以保证各个区带中包括的设施总数与需布置的设施总数相同。

2.3 罚函数

采用本文中设计的编码规则时，可能会超出布置区域范围的限制。由于设施布局为由下而上进行，因此在Y方向上不会有设施超出布置区域，只需要判断最后一列的设施在X方向是否超出区域的边界。采用罚函数对模型中的约束条件进行处理。针对表示不超过X方向边界的约束条件(7)，以及表示设施长宽比处于一定范围内的约束条件(6)，分别设计罚函数。

(9)

(10)

其中C为罚函数，T为较小的惩罚值。

假设Fik为利用式(1)～式(3)计算得到的染色体k的第i个目标函数值，则带有惩罚项的目标值为：

(11)

由于模型中三个目标函数均以最大值为优化目标，因此在算法的迭代过程中，不符合约束条件的染色体会因目标值太小而被淘汰。

2.4 算法步骤

在设计了编码规则、交叉算子、变异算子以及罚函数之后，基于NSGA Ⅱ算法的基本流程，得出多目标设施布局模型的计算步骤如下：

Step 1 生成初始种群。利用随机方法生成规模为N的初始种群Pn，初始化进化代数n=0；虽然随机生成的初始解可能会违反布置区域横向长度的限制，但由于通过引入罚函数，可以在算法迭代过程中淘汰此类个体，因此在生成初始种群时先不需要处理这些不符合约束条件的个体。

Step 2 产生子代种群；

Step 2.1 对Pn解码，得出各布局方案下由dij构成的距离矩阵D以及由sij构成的邻近度矩阵S

Step 2.2 利用D,S以及预先设定的参数，求解各方案下带有惩罚项的目标函数值

Step 2.3 采用快速非支配排序方法，对种群分组，并计算个体拥挤度

Step 2.4 根据拥挤度选择出N/2个个体，组成配对种群Mn。

Step 2.5 对Mn进行遗传操作，产生规模为N的子代种群Cn；

Step 3 种群合并。将Pn与Cn合并，产生规模为2N的种群Rn；

Step 4 产生新的父代种群。根据Step 2.1～Step 2.3计算Rn中每一个非支配层中所有个体的拥挤度，按照拥挤度选择算子，将N个优秀个体遗传到下一代，形成新的父代种群Pn+1；

Step 5 终止判断。如果达到最大迭代次数，则终止计算并输出结果，否则令n=n+1，并返回Step 2。

3 实例分析

为促进区域经济发展，某市计划建设一物流园区。规划占地面积为42万平方米，根据地区腹地产业类型、交通运输网络情况，以及物流园区的功能定位，将其划分为办公区、集装箱堆场、散货堆场、保税监管库、普通仓库、流通加工区、临港工业区、城市配送区、铁路换装区、交易展示区、综合服务区、停车场共12个功能区 (表4)。各功能区之间的物流量、邻近关系、出于环境及安全角度考虑的距离要求如表5。单位货物单位距离的搬运费用设为1，H=500米，D=15米，W=25米，b=4，α=5，β=0.3。

表4 物流园区各功能区面积 (万平方米)

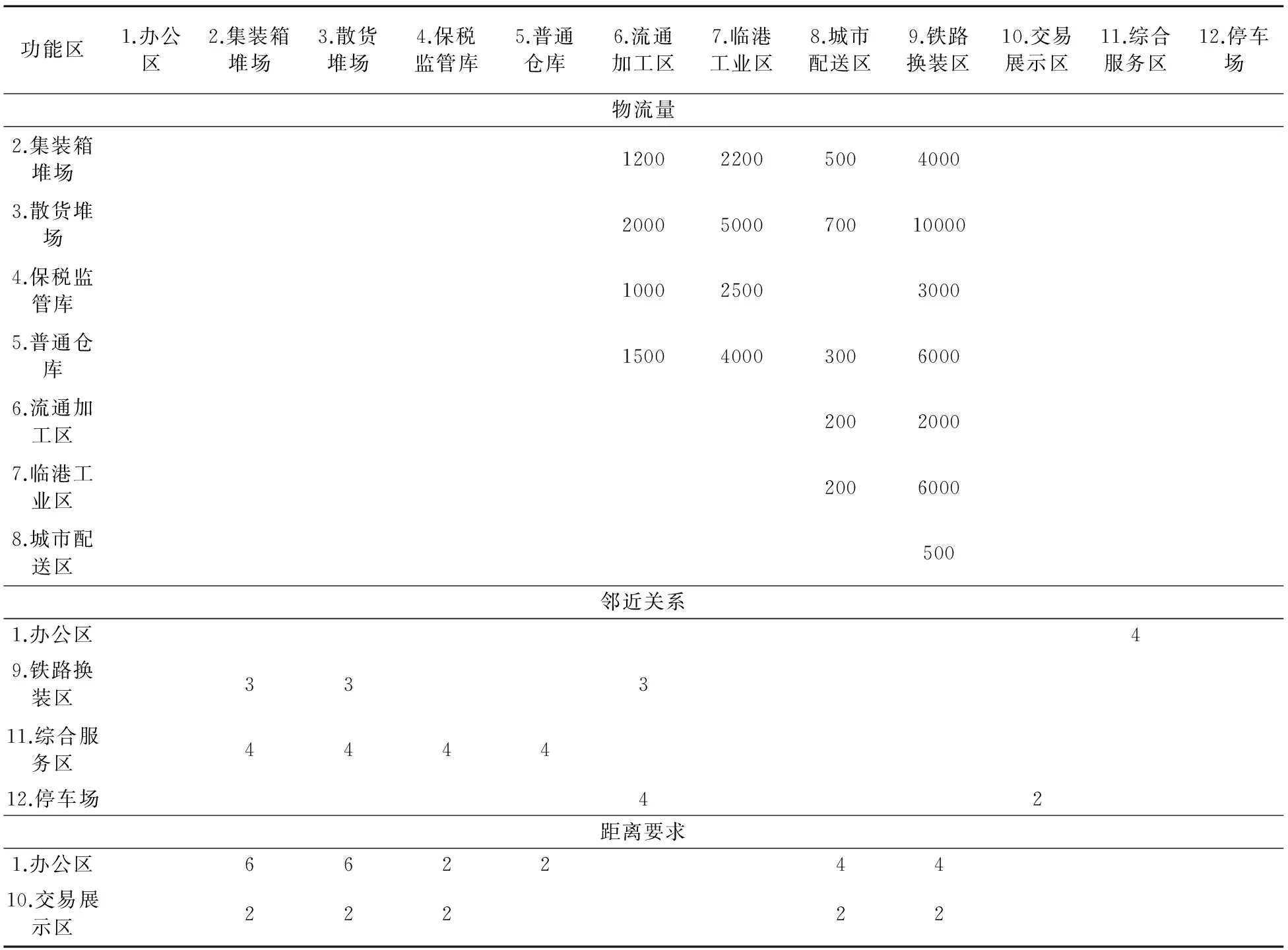
表5 功能区之间物流量、邻近关系、距离要求

NSGA Ⅱ算法的参数设定如下：种群规模取值为100，迭代次数取500，交叉概率取0.7，变异概率取0.05。利用MATLAB软件进行计算，共得到17组Pareto最优解。最优解及对应的目标函数值如表6(其中搬运成本值由式(1)计算得出)。

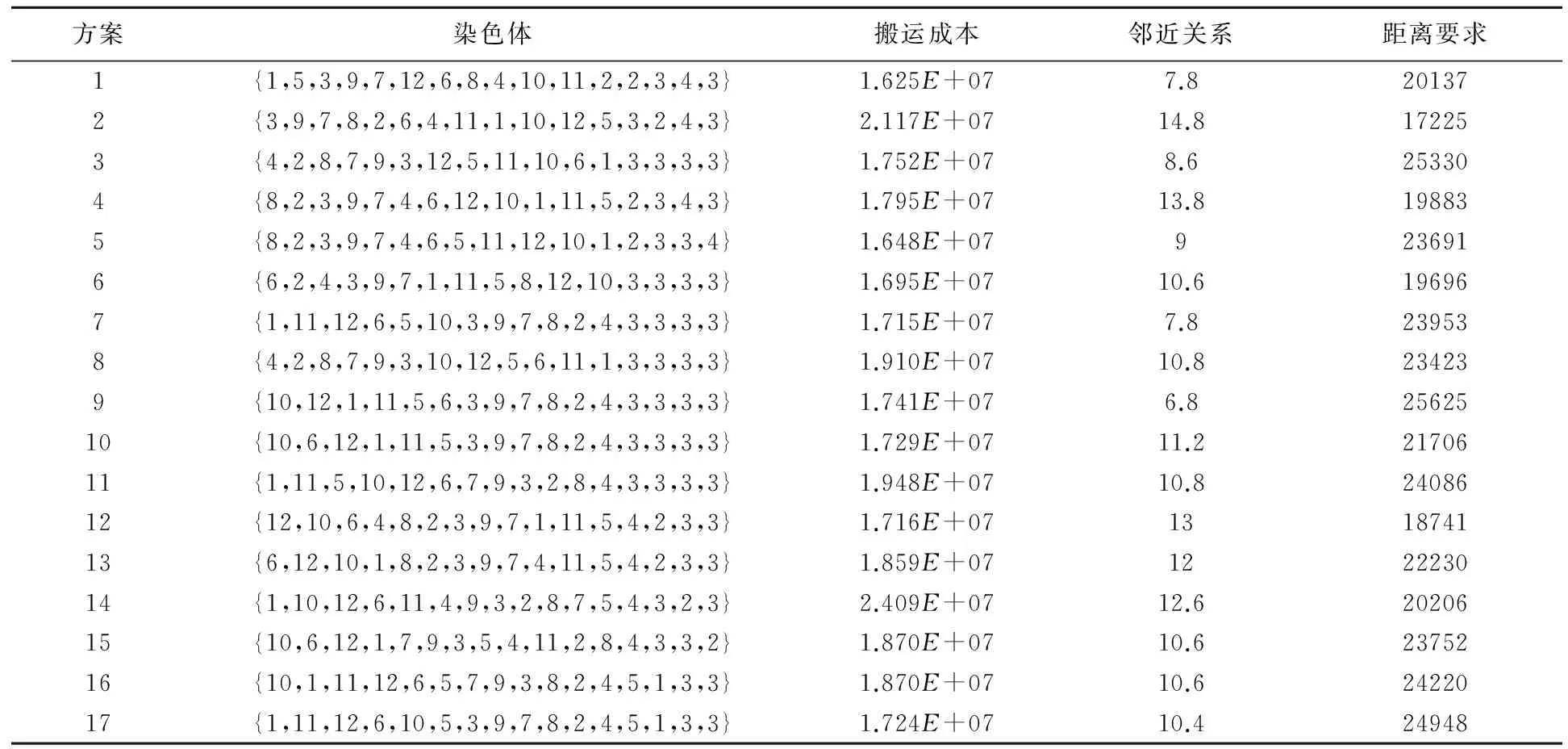
表6 布局方案及相应目标函数值

从表6中的结果可以看出，在种群经过500次迭代之后，布局模型的三个目标的最优值分别为1.625E+07，14.8，25330。表6中前3组的解分别为某一目标达到最优，但是其余两个目标表现不佳；其余的14组解的三项目标函数均未能达到最优，但目标值的平衡性均优于前三组解。表7和图2是1号方案对应的功能区平面布局结果，在该方案下，为实现货物的搬运成本最小，物流量较大的功能区均较为靠近，但成本目标的最低是以另外两个目标的增大为代价的，因此在邻近度和距离要求两方面，1号方案的表现相对较差。

表7 物流园区功能区质心坐标及规模(方案1)

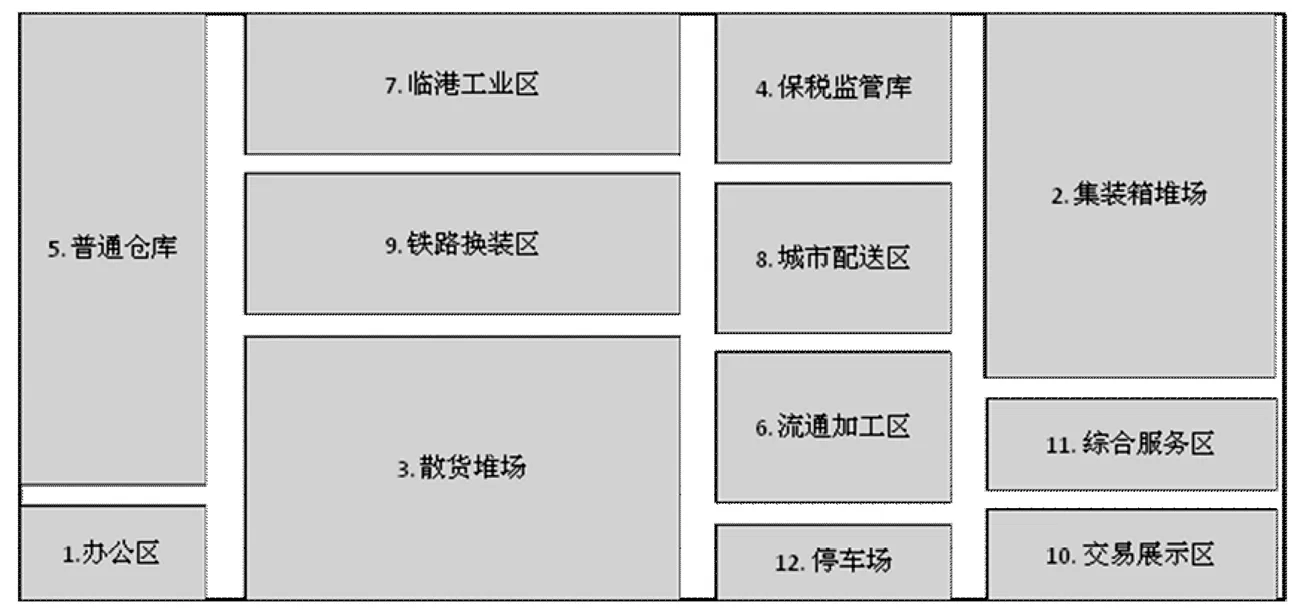
图2 物流园区布局图(方案1)

可以看出，在实际中不并存在使三个目标函数的值均达到最优的布局方案。在具体应用时，决策者可根据实际情况以及未来的规划，从多个布局方案中选择最适合的方案，设计物流园区的功能区布局。同时决策者还可以设置不同的b值，即物流园区内功能区的列数，得到不同的Pareto解集，并互相比较，选择最优的布局方案。

4 结论

设施的合理布局可以有效提升运营效率，降低营运成本。本文构建了可以综合考虑布置区域内设施之间的物料搬运成本、设施间邻近关系、设施间的距离要求的多目标设施布局模型，用于解决弹性区带架构布置形式下，带有固定过道且设施面积不等时的连续型设施布局问题。采用基于NSGA Ⅱ的多目标遗传算法求解，克服了一般的多目标单一化方法需要人为设置子目标函数权重、主观性过强的缺陷。根据问题的特征，设计选择了编码方式、交叉算子、变异算子；并引入罚函数，保证了不合理的染色体在进化过程中被淘汰。最后以某地区的物流园区为例，验证了模型和算法的有效性。设施布局是一个复杂的决策问题，需要考虑大量因素，本文仅选取了物流成本、邻近关系、距离要求作为目标函数，在下一步的工作中，可进一步考虑选取例如员工满意度、空间利用率等其他指标，用于解决设施的平面布局问题。

[1] Tompkins J A, White J A, Bozer Y A, Tanchoco J M A. Facilities planning[M]. New York: Wiley, 2010.

[2] Tong X. SECOT: a sequential construction technique for facility design[D]. University of Pittsburgh, 1991.

[3] Meller R D, Bozer Y A. A new simulated annealing algorithm for the facility layout problem[J]. International Journal of Production Research, 1996, 34(6): 1675-1692.

[4] Kulturel K S, Smith A E, Norman B A. Bi-objective facility expansion and relayout considering monuments[J]. IIE Transactions, 2007, 39(7): 747-761.

[5] Wong K Y, Komarudin. Solving facility layout problems using flexible bay structure representation and ant system algorithm[J]. Expert Systems with Applications, 2010, 37: 5523-5527.

[6] Kulturel K S, Konak A. A new relaxed flexible bay structure representation and particle swarm optimization for the unequal area facility layout problem[J]. Engineering Optimization, 2011, 43: 1-25.

[7] 郑永前,丁奎学.基于改进粒子群算法的制造单元设施布局问题研究[J].工业工程,2012,15(1):125-130.[8] Haktanirlar U B, Kulturel K S. An artificial immune system based algorithm to solve unequal area facility layout problem[J]. Expert Systems with Applications, 2012, 39: 5384-5395.

[9] Muther R. Practical plant layout[M]. New York: McGraw-Hill College, 1955.

[10] 杨薇.基于遗传算法的双目标设施布置方法研究 [D].天津大学,2010.

[11] Rosenblatt M J. The facility layout problem: a multi-goal approach[J]. International Journal of Production Research, 1979, 17(4): 323-332.

[12] Ardestani J A, Krishnan K, Hashemi D H, Davoudpour H. A multi-objective formulation for facility layout problem[C]. In: Proceedings of the World Congress on Engineering and Computer Science, San Francisco, California, 2009: 46-51.

[13] 曾强,沈玲,潘启东,吴立云.基于NSGAⅡ的多目标车间设施布局优化方法[J].计算机工程与应用,2012,48(27):223-228.

[14] Schaffer J D. Multiple objective optimization with vector evaluated genetic algorithms[C]. In: Proceedings of the 1st International Conference on Genetic Algorithms, Hillsdale, New Jersey, 1985: 93-100.

[15] Horn J, Nafpliotis N, Goldberg D E. A niched pareto genetic algorithm for multiobjective optimization[C]. In: Proceeding of 1st IEEE Conference on Evolutionary Computation, Orlando, Florida, 1994: 82- 87.

[16] Srinivas N, Deb K. Multi-objective function optimization using non-dominated sorting genetic algorithms[J]. Evolutionary Computation, 1995, 2(3): 221-248.

[17] Zitzler E, Thiele L. Multi-objective evolutionary algorithms: a comparative case study and the strength pareto approach[J]. IEEE Transactions on evolutionary computation, 1999, 3(4): 257-271.

[18] Deb K. A fast and elitist multiobjective genetic algorithm: NSGA II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

[19] Lee K Y, Rob M I, Jeong H S. An improved genetic algorithm for multi-floor facility layout problems having inner structure walls and passages[J]. Computer Operations Research, 2003, 30(1):117-138.

[20] DeJong K A. An analysis of the behavior of a class of genetic adaptive systems[D]. University of Michigan, 1975.

Analysis of Multi-objective Facility Layout Problem Using Flexible Bay Structure

CHANG Zheng, LU Jing

(TransportationManagementCollege,DalianMaritimeUniversity,Dalian116026,China)

In order to solve continuous unequal area facility layout problem, a multi-objective facility layout model is proposed in the representation of flexible bay structure. The model aims to minimize material handling cost, to maximize adjacency rating and to maximize distance request. The model also takes vertical and horizontal aisles as well as aspect ratio constraints of facilities into consideration, which makes the layout more realistic. In order to overcome the disadvantage of subjectivity caused by the artificial weights of multiple objectives of conventional simplification method, a multi-objective optimization algorithm based on Non-dominated Sorting Genetic Algorithm Ⅱ(NSGA Ⅱ)is proposed as the solving technique. At the same time, the corresponding encoding rule, cross operator, mutation operator and penalty function are designed. The empirical analysis of a logistics park confirms the effectiveness of the proposed model and methodology as a practicable tool for facility layout designers.

industrial engineering; facility layout; flexible bay structure; unequal area; NSGA Ⅱ; logistics park

2013- 03-26

中央高校基本科研业务费大连海事大学青年教师科技创新项目(3132014083)；教育部哲学社会科学研究重大课题攻关项目(11JZD049)

常征，女，博士，讲师。

TB491;F406.2;F540.5

A

1007-3221(2015)02- 0128- 07