工期索赔中的难题
张立辉, 熊 俊, 刘树良, 乞建勋
(1.华北电力大学 经济与管理学院,北京 102206; 2.华北电力大学 经济与管理学院,河北 保定 071003)
工期索赔中的难题
张立辉1, 熊 俊1, 刘树良2, 乞建勋1
(1.华北电力大学 经济与管理学院,北京 102206; 2.华北电力大学 经济与管理学院,河北 保定 071003)
针对重大工程计划中工期索赔的责任划分难题,本文根据公路建设中的实际案例,发现了“工期索赔分摊”中的奇怪现象。首先,揭示了“提前完成任务”不但可能得不到“奖励”,反而可能要被“罚款”;其次,揭示了关键工序的工期提前完成较少时,会得到“奖励”,但提前得太多,则反而会被“罚款”。然后,给出了解决这些奇怪现象的解释和方法。这些现象说明了在处理重大工程计划的“索赔款分摊”时,不能只按传统的原则来处理,必须根据实际情况按新的规则来处理。研究结论对于促进工期索赔的合理分摊有一定的理论意义和现实意义。
公路建设;奇异现象;工期索赔;关键工序;重大工程计划
0 引言
在工程管理中,工期索赔是一项重要的管理工作。如果总工期被延误,业主要向施工方索赔,而施工方则要追究责任,处理造成总工期延误的团体或个人[1,2]。这就涉及到责任的分摊问题。而责任的分摊不但是体现实际的工作,更是涉及到一系列的重大理论问题[3~6]。在过去,人们研究的重点放在责任分摊的政策问题上,以及行为科学中的人际关系问题上,尤其是公平原则问题上[7~10]。之所以这样做,认为造成总工期的原因是很容易搞清楚的,如,一个工序的工期没有延长甚至还提前完成任务,则该工序的人对总工期的延误就不负有责任。相反,如果一个工序的工期延误,则应当对总工期的延误负有相应的责任。工序延误的工期越多,则负的责任应当越大。这些规律和原则是众所周知的,没有着重研究的必要,因而考虑更多的是政策和策略问题。
但是随着科学技术的迅猛发展以及经济国际化的特点,重大工程项目迅速增多。重大项目的特点是投资多、工期长,一般少则几亿,多则上百亿,时间也少则一二年,多则七八年、十来年。工期时间的拉长,遇到各种不确定的因素、不可知的因素越多,因而总工期延误的可能性就增大。又因为工程投资巨大,哪怕是造成万分之一的误差,也会是成千上亿的损失,所以重大工程项目的计划管理越来越受到人们的高度重视。各国都投入了大量的人力、物力来研究重大工程计划的规律。例如,我国自然科学基金委管理学部在2013年就曾立项1000万元的一项软科学项目,研究我国城市基础设施建设中的问题和规律。文献[11]则调查了亚洲银行资助的100项重点项目,其中86%的项目总工期都要延误;文献[12]调查了韩国的重大工程完工情况,发现10亿美元以上的项目中,平均总工期推迟3.6年,而10亿美元以下5000万美元以上的项目中,总工期平均推迟2.4年;文献[13]则揭示了美国258个铁路桥梁、隧道和公路建设项目,其总工期平均延长17%。事实上,重大工程总工期的延误已成为世界性的现象。
重大工程总工期的普遍延误,使工期索赔问题变得更加突出,尤其是重大工程计划的索赔数量巨大,因而使业主与施工方的矛盾更加激烈。由于总工期延误是由于人为的原因还是因为不可预测的随机因素,对于索赔款的数量有着重要的影响,因此,施工方总是强调总工期长,随机干扰因素多;而业主则强调由于科技的发展,计划控制和调整的能力较过去有了很大的提高,多年的施工经验也越来越丰富,因而抗干扰的能力极大提高,不应当出现总工期延误越来越多的情况,认为这主要是人为因素造成的[14~16]。对于延误原因的不同认识,经常造成在索赔款数量上的巨大争执。因此,研究重大工程总工期延误的真正原因越来越成为工期索赔的重大理论问题[17]。而了解重大工程总工期延误的真正原因,就必须研究重大工程计划的新规律。本文正是抱着这种目的,展开了对重大工程计划规律性的研究。
研究一种事物规律的捷径是寻找该事物的奇异现象,因为奇异现象恰恰是该事物新规律所显现的新信息。下面我们首先研究一个实际的案例,然后研究这个案例中体现出的奇怪现象。
1 工程计划实际案例一
要修建一条7.2公里长的公路,分三段实施k1,k2,k3,每段长度为2.4公路。路面结构分为三个结构
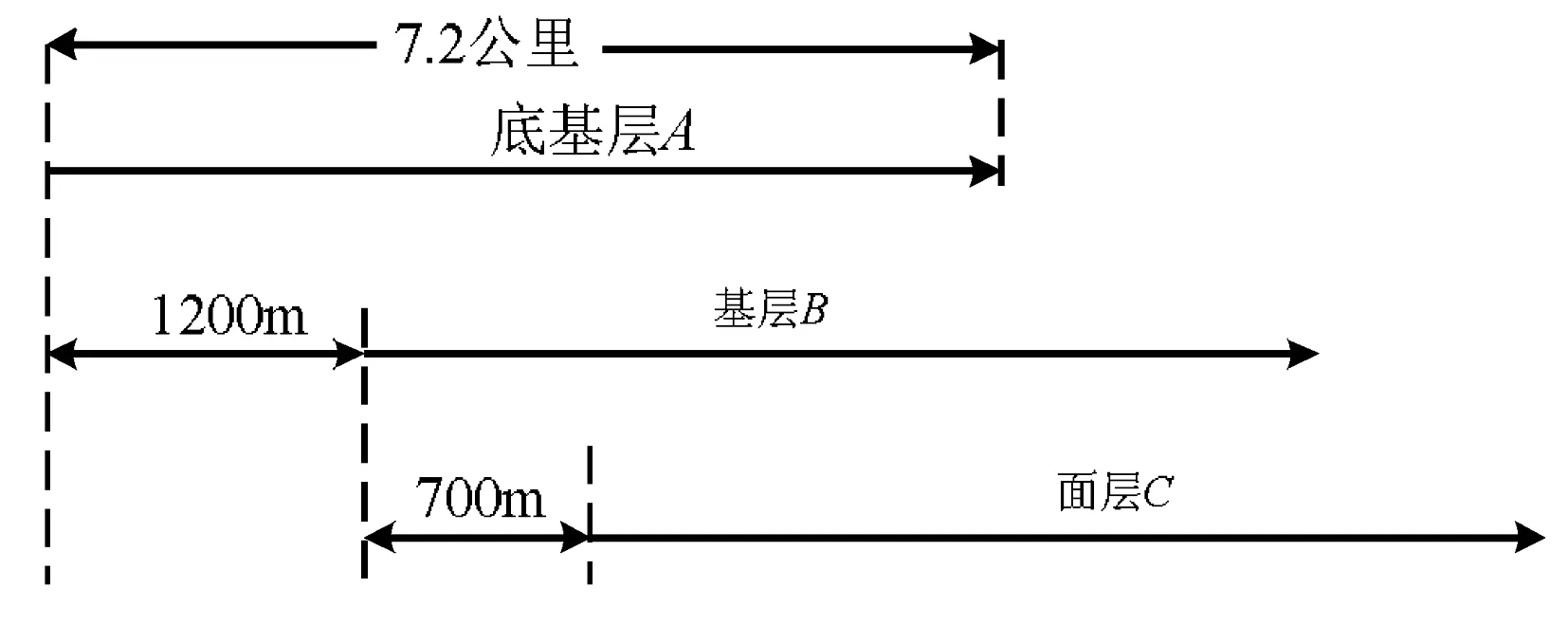
图1 公路项目三层约束关系示意图
层:底基层A:挖沟,筑堤,砂石铺路等;基层B:水泥路面的浇注等;面层C:施工的安装及修饰等。三层均采用线性流水施工,即Ak→Bk→Ck。底基层Ak和基层Bk之间,基层Bk需要的最小工作面的长度为1200米;基层Bk与面层Ck之间,面层Ck需要的最小工作面长度为700米,如图1所示。
由于k1,k2,k3各段地层条件复杂,各段的施工速度也不相同,如表1所示。

表1 公路项目各工序施工速率
则各段的施工工期如下:
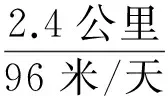
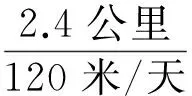

两层之间的施工面的工期,总是在前后道工序之间按快的速度计算。所以,Ak与Bk之间的工作面的工期按Bk的速度计算,
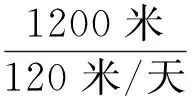
因Bk的速度比Ck的速度快,所以Bk与Ck之间的工作面的工期也按Bk速度计算,
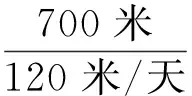
在实际工程中,确定两个工序之间的时间约束类型是“开始—开始”型即“S-S”型还是“结束—结束”型即“F-F”型,按下面的原则来处理:
(1)如果前道工序的施工速度比后道工序的施工速度慢,则采用“F-F”型。
因为Ak的速度96米/天,87米/天,80米/天,分别比Bk的速度120米/天,110米/天,100米/天要慢,所以Ak与Bk”之间采用“F-F”型时间约束,即

(2)如果前道工序的施工速度比后道工序施工速度快,则采用“S-S”型时间约束。
因为B1,B2,B3的速度120米/天,110米/天,100米/天,分别比C1,C2,C3的速度100米/天,90米/天,84米/天要快,所以Bi与C”i之间采用“S-S”型时间约束,即
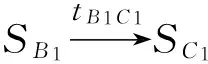
又因基层路面是水泥结构,需要5天的水泥硬化时间,所以SB1与SC1不但要有6天的工作面等待时间,还有水泥硬化5天时间,共有(6+5)=11天的等待时间即
同理,
综上所述,列出下表2以利作图。

表2 公路项目基本信息表
由表2画出单节点搭接网络图,如图2所示。

图2 公路施工计划单节点搭接网络图
如果把每个时间约束都化成“F-S”型时间约束,就可以画出等效的CPM网络图。
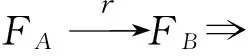
同理可证:
利用这两个公式可以把表2的所有时间约束都化成“F-S”型,由此得图2的等效CPM网络图3。

图3 公路施工计划等效CPM图
注:在CPM中,如图3中,每个工序先计算最早开始,后计算最早结束。但在单节点搭接网络图2中,有些工序先计算最早结束,后计算最早开始。最迟开始与最迟结束的计算也类似。
2 索赔款分摊的难题
2.1 对案例一的索赔分析
在图2、3的公路施工计划中,实际总工期903天,延误了3天,因此按合同索赔3万元。对施工方,这3万元的索赔款如何分摊?
经调查,计划中所有工序都没有拖延工期,而且“基层B3”中,由于改进了操作方法还缩短了3天完成了任务。
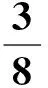
理由:只有基层B3提前完成任务,所以不分摊,其他工序平均分摊。
缺点:其他工序并没有拖延工期,按期完成任务,还被罚款,不能服人心。
分摊方案(二):三万元的索赔款全部由缩短3天完成任务的“基层B3”工序承担,其他工序按时完成任务不罚款。
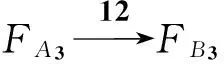
理由:基层B3未经请示允许,擅自缩短3天完成任务,造成总工期延误3天,如图4所示。如果B3不提前完成任务而是按期完成任务,如图2、3所示,总工期不会被推迟。
结论:在重大工程计划,如图4所示,有时提前完成任务不一定是好事,提前完成任务反而可能推迟总工期。因此在索赔款的分摊时,不能认定提前完成任务的就不受罚,要根据具体情况而定。
其等效的CPM网络如图5所示。
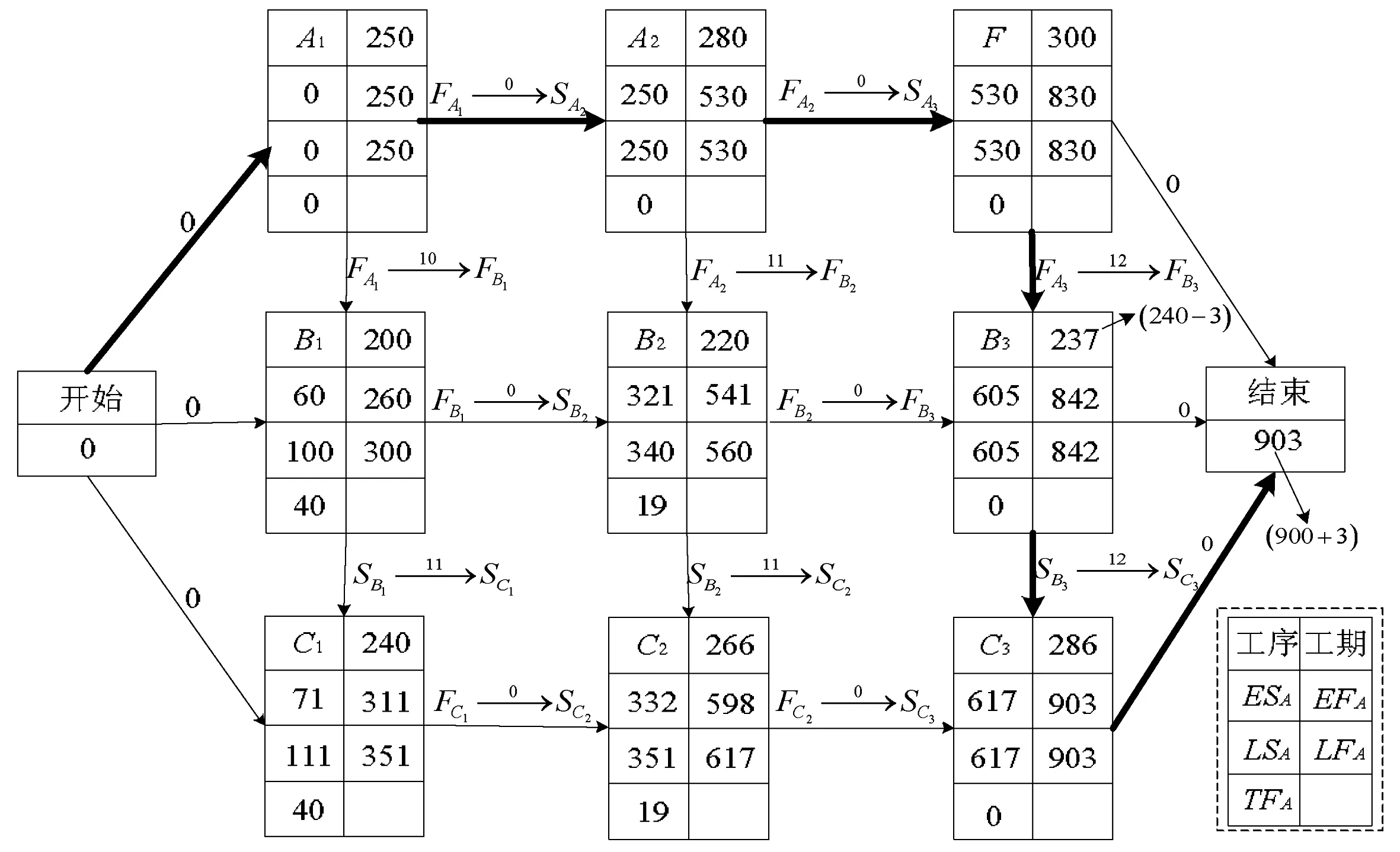
图4 tB3减少3天,总工期增加3天示意图

图5 等效CPM图
理论解释:为什么提前完成任务反而会导致总工期的推迟呢?
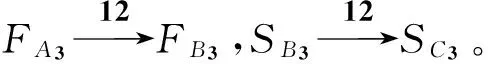


除了这个条件发生这种奇怪现象外,是否还有其他的条件也可产生这种现象,则是需要继续的课题。
由图4与图5可以看出,虽然它们的计算结果完全相同,但从图4看不出关键工序B3的工期压缩3天,总工期反而延长3天的原因,而图5则可看到原因很清楚。可见,在搭接网络中单节点的网络图表示功能不如双节点的网络图。
2.2 对案例二的索赔分析
图6是一个新工程计划网络图(建模过程省略)。
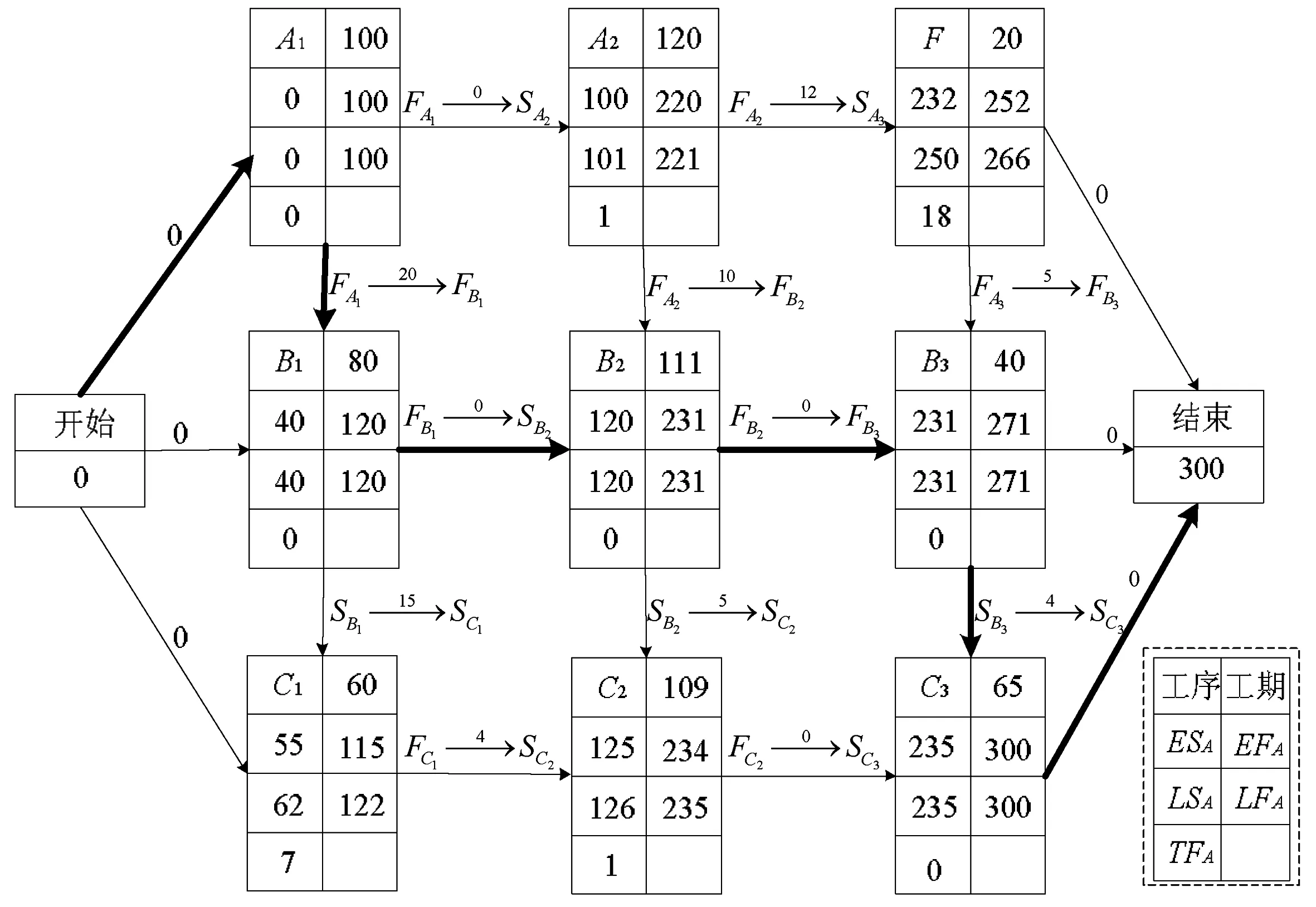
图6 案例二单节点搭接网络图
该计划执行结果,总工期延期1天,变成301天,因此索赔一万元。问如何分摊?
经调查结果:关键工序B3拖延工期4天,40天的任务44天才完成,关键工序B2完成任务的时间缩短了3天,111天任务108天完成,其他工序都按期完成。
方案(一):B3延期4天,罚款4万元,提前3天,奖励3万元,剩下(4-3)=1万元支付索赔款。
理由:B3在关键路线上,工期推迟4天,总工期应当推迟4天,所以应当罚款4万元,关键工序B2提前3天,总工期应当缩短3天,因此总工期延长(4-3)=1天。所以,B2应当奖励3万元。多出(4-3)=1万元用于索赔款。
方案(二):B2虽然提前3天完成任务,但仍需罚款一万元,支付索赔款;B3虽拖延了4天,但总工期没受影响,所以不能算罚款,其他工序按期完成任务,不奖不罚。
理由:(1)如果B2按期完成任务,不提前,而仅仅是B3延期4天,则总工期不变,如图7和图8所示。
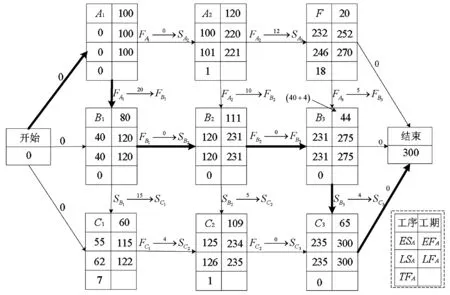
图7 B3延期4天,总工期不变
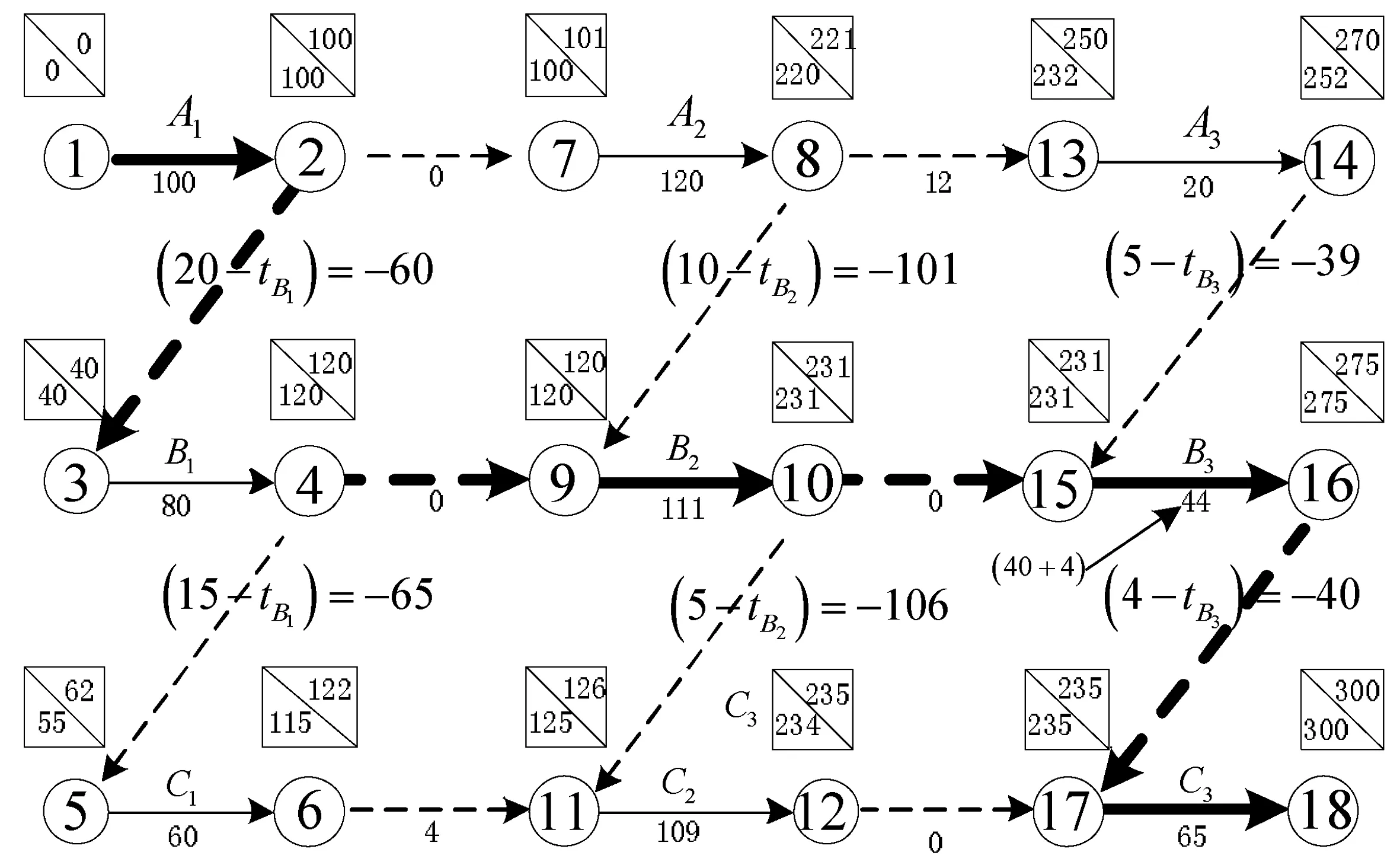
图8 等效CPM图
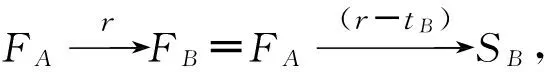
得等效CPM网络图8。
从图8可以看出,当B3的工期延长4天,(15,16)的工期延长4天,但(16,17)的工期(4-tB3)反而减少4天。(15,16)和(16,17)都在同一条关键路线上,所以B3的工期tB3延长4天,总工期不变。但是单节点的图7就不容易看出这个原因,所以搭接网络图应当用双节点的网络图表示。
(2)如果关键工序B2的工期压缩1天,B3等其他工序都不变,则总工期也缩短1天,如图9所示。
在传统的CPM网络中,关键工序的工期压缩1天,总工期也压缩1天,那么关键工序的工期压缩3天,总工期也可能缩短3天,也可能就只能压缩1天,但无论如何,关键工序的工期再继续压缩,总工期绝不会增长。而在我们搭接网络的这个例题中,关键工序B2虽然工期压缩1天时,总工期缩短1天,但关键工序B2的工期压缩3天时,总工期不但不继续缩短,反而延长1天,如图10所示。
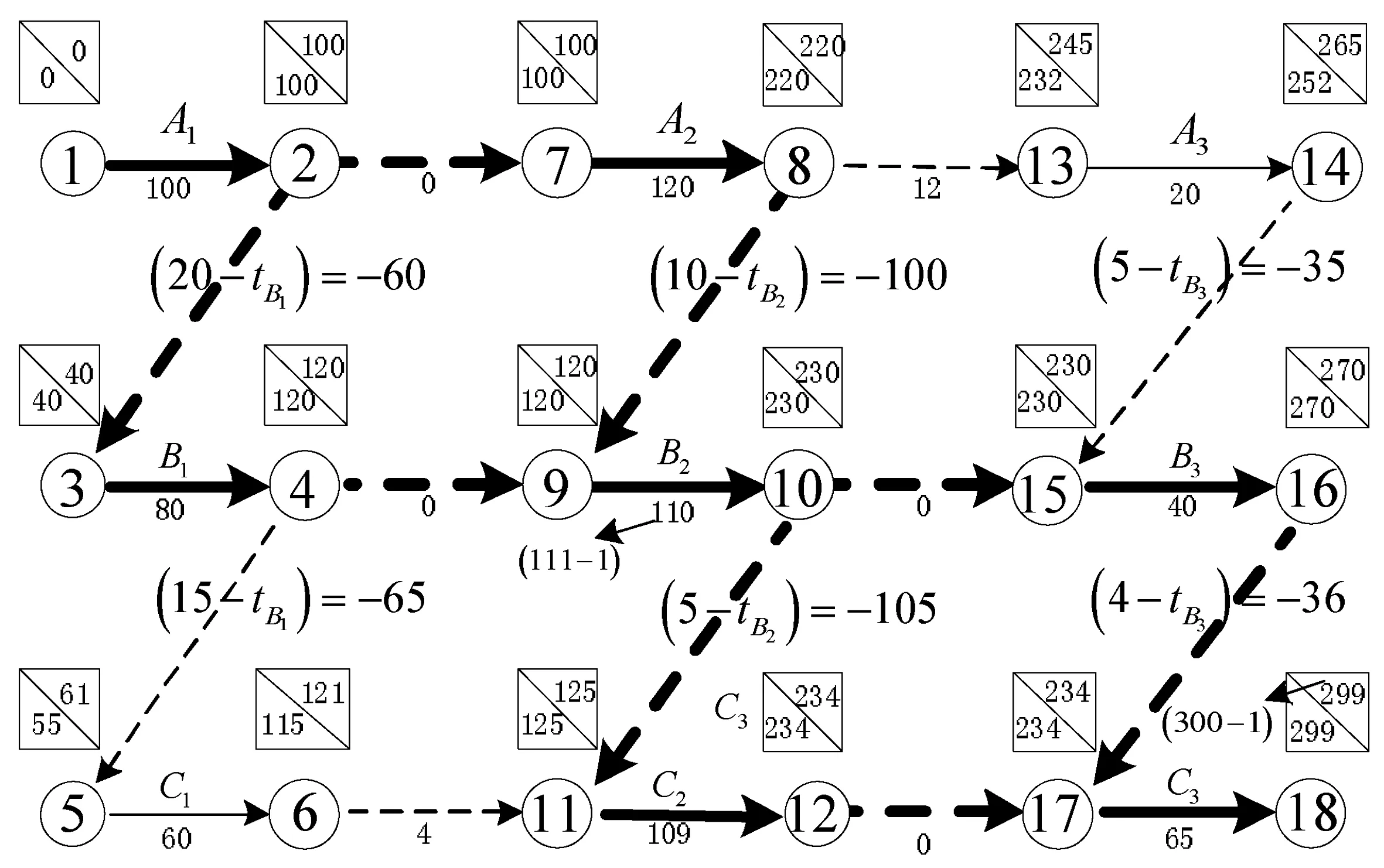
图9 B2的工期压缩1天,总工期缩短1天
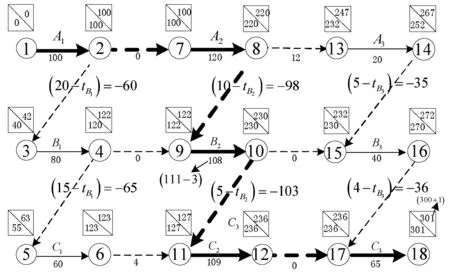
图10 关键工序B2工期减少3天,总工期增加1天
理论解释:由图8和图9可以看出,在B2的工期减少1天后,出现了新关键路线μ▽′。
μ▽=(1)→(2)→(3)→(4)→(9)→(10)→(11)→(12)→(17)→(18)减少1天。
B2的工期再继续减少2天时,新关键路线μ▽′,
μ▽′=(1)→(2)→(7)→(8)→(9)→(10)→(11)→(12)→(17)→(18)增加2天。
因而,总工期增加(2-1)=1天。因为B2工期减少3天,总工期不但没减少反而增加1天,而B3工期增加4天,不影响总工期,所以B2减少3天,B3增加4天,总工期只增加1天,如图9和图10所示。所以,工期提前完成3天的关键工序B2应罚款一万元。而工期拖延4天的关键工序B3不应受处罚。
等效CPM图如下:

图11 B2工期减少3天,B3工期延长4天,总工期延长1天
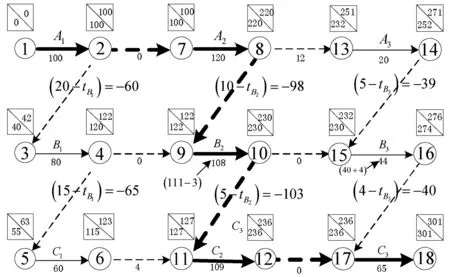
图12 等效CPM图
3 结论
(1)在搭接网络中,存在一类关键工序,其工期变化,总工期不变,如B3。
(2)在搭接网络中,关键工序工期压缩量小时,总工期缩短,但压缩量太大,总工期不但不能继续缩短,反而可能延长,如图8中的B2。
(3)在重大工程计划中,存在一些非传统的时间约束,如“F-F”,“S-S”等。由于这些时间约束的存在,重大工程计划的规律与CPM完全不同,因此在“工期索赔分摊”时,不能再简单的沿用过去的传统观念,要通过计算,具体情况具体分析。这里的规律性还需要进一步研究。
[1] 马铁焰.《水利水电土建工程施工合同条件》下的业主索赔[J].四川水力发电,2006,S2:62- 64.
[2] Bunni N G. The FIDIC form of contract: the fourth edition of the red book[M]. Oxford: Blackwell Science, 1997.
[3] Hinze J W. Construction planning and scheduling[M]. Pearson Higher Ed, 2011.
[4] 苏志雄,乞建勋,阚芝南.求解CPM网络计划的最大网络时差[J].运筹与管理,2014,01:33-38.
[5] 乞建勋,张立辉,李星梅.网络计划管理中的机动时间的特性理论及其应用[M].北京:科学出版社,2009.
[6] 乞建勋,李星梅,王强.等效子网络构建的理论与方法[J].管理科学学报,2010,(1):40- 44.
[7] 刘英杰,孟凡玲,冯平.基于总时差分配的工期索赔研究[J].水电能源科学,2010,(2):122-124.
[8] 秦浩安.工期延误如何索赔[J].施工企业管理,2014,10:34-35.
[9] 张丽霞,韦福祥.工期索赔中的工序延迟分析[J].数学的实践与认识,2007,07:20-26.
[10] 吕胜普,李建设,杨飞雪.多事件交叉干扰下的工期索赔方法[J].土木工程学报,2005,11:112-116+127.
[11] Kamrul Ahsana, Indra Gunawan. Analysis of cost and schedule performance of international development projects[J]. International Journal of Project Management, 2010, 28(1): 68-78.
[12] Han S H, Yun S, Kim H, et al. Analyzing schedule delay of mega project: lessons learned from korea train express[J]. Engineering Management, IEEE Transactions on, 2009, 56(2): 243-256.
[13] Flyvbjerg B. Mega delusional: the curse of the mega project[J]. New Scientist, 2013, 220(2945): 28-29.
[14] Adam A, Josephson P E, Lindahl G. Implications of cost overruns and time delays on major public construction projects[C]. Proceedings of the 19th International Symposium on the Advancement of Construction Management and Real Estate, 7-9 Nov 2014, Chongqing. 2014.
[15] Aigbavboa C O, Thwala W D. An exploratory study of the major causes of construction disputes in the south african construction sector[C]. Applied Research Conference in Africa, 2014.
[16] Hwang B G, Zhao X, Ng S Y. Identifying the critical factors affecting schedule performance of public housing projects[J]. Habitat International, 2013, 38: 214-221.
[17] Yang J B, Kao C K. Critical path effect based delay analysis method for construction projects[J]. International Journal of Project Management, 2012, 30(3): 385-397.
The Difficult Problems in Time Claims
ZHANG Li-hui1, XIONG Jun1, LIU Shu-liang2, QI Jian-xun1
(1.North China Electric Power University, School of Economics and Management, Beijing 102206; 2.North China Electric Power University(Baoding), School of economics and management, Baoding 071003, China)
According to the division of responsibility about time claims in major projects scheduling, the anomalies in the time claims are found in this paper based on the actual case in highway construction. Firstly, it reveals that there will be a fine when the activity is fulfilled ahead of time; secondly, there will be a reward when the critical activity is compressed to a certain threshold. However, there will be a fine when the amount of compression is larger than the threshold; and finally, the method and interpretation are presented to solve and analyze these anomalies. These anomalies explain that the new rule must be considered when the time limit for a project claim contribution occurs in major projects. The conclusions of the research have certain theoretical significance and practical significance for promoting time claims.
highway construction; anomalies; time claims; critical activity; major projects
2014- 01-23
国家自然科学基金资助项目(71171079,71271081);中央高校基金(13zd08)
张立辉(1974-),男,湖南人,教授,博士,研究方向:管理科学与工程。
TB114.1
A
1007-3221(2015)03- 0266- 09

