对模糊数互补判断矩阵乘性一致性的重新认识

石喜军， 张 强， 朱吉乔

(1.北京理工大学 管理与经济学院，北京 100081； 2.北京建筑材料科学研究总院，北京 100041)



对模糊数互补判断矩阵乘性一致性的重新认识

石喜军1， 张 强1， 朱吉乔2

(1.北京理工大学 管理与经济学院，北京 100081； 2.北京建筑材料科学研究总院，北京 100041)

为了解决模糊数间的加和减、乘和除已不再是逆运算的问题，并使得运算法则更加符合客观实际情况，而引入了经典数学中的自变量、因变量、代表系统及自由度等概念，进而对模糊数互补判断矩阵的乘性一致性进行了研究，结果发现若一个模糊数互补判断矩阵满足目前一些文献对其乘性一致性的定义则这个矩阵一定是精确数互补判断矩阵这一不合理之处。文章最后结合模糊集截集理论，利用模糊数互补判断矩阵元素间的关系，重新对乘性一致性模糊数互补判断矩阵进行了定义。

管理科学与工程；代表系统；模糊集理论；模糊数互补判断矩阵；自变模糊数；因变模糊数

0 引言

通过研究方案间两两比较建立的判断矩阵，人们可以对方案进行决策选择。然而由于决策者自身主观认识的局限性以及客观事物的复杂性和不确定性，带有模糊信息的模糊互补判断矩阵越来越受到决策者的重视。根据指标值的不同，模糊互补判断矩阵可分为指标值是精确数的模糊互补判断矩阵(简称精确数互补判断矩阵)和指标值是模糊数的模糊互补判断矩阵(简称模糊数互补判断矩阵)。根据构造方式的不同，模糊互补判断矩阵又可分为基于加性一致性的模糊互补判断矩阵和基于乘性一致性的模糊互补判断矩阵。毫无疑问，无论根据怎样的构造方式建立模糊互补判断矩阵，对其一致性的研究都将是一个很重要的内容。

目前，精确数互补判断矩阵和基于加性一致性的模糊数互补判断矩阵的一致性研究已经取得了丰硕成果[1～8]。然而，由于模糊数乘法的特殊性，关于模糊数互补判断的乘性一致性的研究，虽然取得一些成果，但进展相对缓慢。文献[9]首次给出了三角模糊数互补判断矩阵的概念，并提出一种基于可能度的三角模糊数互补判断矩阵的排序方法，这可看作是模糊数互补判断矩阵研究的萌芽；文献[10]研究了区间数互反判断矩阵和区间数互补判断矩阵之间的转换关系，并给出了乘性一致性区间数互补判断矩阵的定义，然而，文献[11]指出，满足文中定义的乘性一致性区间数互补判断矩阵并不存在；文献[12]研究了决策信息以三角模糊数互补判断矩阵形式给出的多属性决策问题，并仿照乘性一致性精确数互补判断矩阵的概念，定义了乘性一致性三角模糊数互补判断矩阵，然而下文将要证明，文献[12]所定义的乘性一致性三角模糊数互补判断矩阵也不存在。

本文首先为了解决模糊数间的加和减、乘和除已不再是一对逆运算的问题，并使得运算法则更加符合客观实际情况，而把经典数学理论中的自变量、因变量、代表系统和自由度的概念引入到了模糊集理论中，进而对文献[12]的定义的乘性一致性三角模糊数互补判断矩阵进行了研究，结果发现若一个三角模糊数互补判断矩阵满足[12]定义的乘性一致性则这个矩阵一定是精确数互补判断矩阵这一不合理之处。紧接着，通过引入导出精确数互补判断矩阵和共轭精确数互补判断矩阵的概念，对乘性一致性区间数互补判断矩阵和乘性一致性模糊数进行了重新定义

1 预备知识

(1)

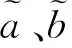
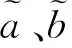
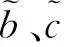
定义3[15]矩阵P=(pij)n×n，其中pij为精确数，若pij+pji=1, ∀i,j,则称P=(pij)n×n为精确数互补判断矩阵。

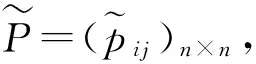
对模糊数互补判断矩阵研究最多的是Ⅰ型模糊数[8](区间数、三角模糊数和梯形模糊数)互补判断矩阵，而无论何种模糊数互补判断矩阵，都可以如下定义：

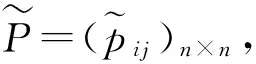
2 模糊数互补判断矩阵的乘性一致性

关于精确数互补判断矩阵，Tanino T曾给出如下乘性一致性定义：

定义6[17]精确数互补判断矩阵P=(pij)n×n，若pikpkjpji=pkipjkpij，∀i,j,k，则称P为乘性一致性精确数互补判断矩阵。

由矩阵中元素间的互补性可知

(2)

徐泽水曾仿照Tanino T的定义，给出了乘性一致性三角模糊数互补判断矩阵的定义：

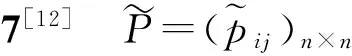
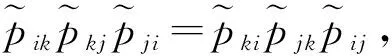
(3)

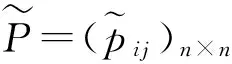
(4)

(5)

从而

(6)

显然，在公式(6)中，∀i,j,k，xij、xik和xkj的自由度为2。现在假设xik和xkj为自变量，xij为因变量(其它情况类似)，由前可知，xij、xik和xkj一定满足下面两个条件：

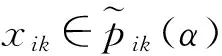
由于任意Ⅰ型模糊数的α-截集均为区间数，因此这里可以先定义乘性一致性区间数互补判断矩阵，进而利用模糊集截集理论对乘性一致性模糊数互补判断矩阵进行定义。区间数可看作某一区间的精确数的集合，而精确数互补判断矩阵的乘性一致性研究已经相当成熟，为了充分利用其研究成果，可先定义乘性一致性区间数互补判断矩阵。

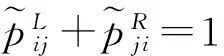
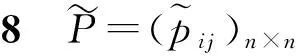
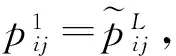
显然，在一个n×n的区间数互补判断矩阵中，共有2k个导出精确数互补判断矩阵和2k-1对共轭精确数互补判断矩阵，其中k=n(n-1)/2为原区间数互补判断矩阵的自由度。有了以上导出精确数互补判断矩阵和共轭精确数互补判断矩阵的定义，可以对区间数互补判断矩阵进行如下定义：

例1 有一区间数互补判断矩阵

如果令

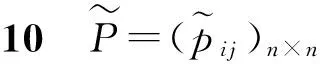
3 结束语

根据模糊理论中的运算法则，模糊数间的加和减、乘和除运算已经不再试逆运算，本文通过深入剖析造成这一结果的原因，为使模糊数间的运算法则更能符合客观的实际情况，引入了经典数学中的自变量、因变量、代表系统和自由度等概念，进而对文献[12]中乘性一致性三角模糊数互补判断矩阵定义进行了分析，得出满足文献[12]定义的乘性一致性三角模糊数互补判断矩阵并不存在。为了合理定义乘性一致性模糊数互补判断矩阵，文章对区间数互补判断矩阵的定义进行了研究，通过引入导出精确数互补判断矩阵和共轭精确数互补判断矩阵的概念，对乘性一致性区间数互补判断矩阵和乘性一致性模糊数互补判断矩阵给出了一个合理的定义。

[1] Xu Z S. Two approaches to improving the consistency of complementary judgment matrix[J]. Applied Mathematics: A Journal of Chinese Universities(Series B), 2002, 17: 227-235.

[2] Xu Z S, Da Q L. An approach to improving consistency of fuzzy preference matrix[J]. Fuzzy Optimization and Decision Making, 2003, 2: 3-12.

[3] 徐改丽,林亮.基于模糊互补判断矩阵的一致性调整新方法[J].运筹与管理,2011,20(1):93-97.

[4] 刘颖芬,占济舟.FAHP中的一致性与标度[J].东北师大学报(自然科学版),2010,42(2):27-30.

[5] 杨莉,李南,和媛媛.三角模糊数互补判断矩阵的加性一致性及排序[J].系统工程,2009,27(3):89-92.

[6] 钱钢,冯向前,徐泽水.区间数互补判断矩阵的一致性[J].控制与决策,2009,24(5):723-728.

[7] 侯福均,吴祈宗.模糊数互补判断矩阵的加性一致性[J].北京理工大学学报,2004,24(4):367-372.

[8] 侯福均,吴祈宗.Ⅰ型不确定数互补判断矩阵的一致性和排序研究[J].系统工程理论与实践,2005,10:60- 66.

[9] 徐泽水.三角模糊数互补判断矩阵的一种排序方法[J].模糊系统与数学,2002,16(1):47-50.

[10] 巩在武,刘思峰.区间数互补判断矩阵的性质及相关问题研究[J].运筹与管理,2006,15(3):25-30.

[11] 朱吉乔,张强,赵璇.模糊数互补判断矩阵的乘性一致性研究[J].运筹与管理,2013,22(1):29-35.

[12] 徐泽水.三角模糊数互补判断矩阵排序方法研究[J].系统工程学报,2004,19(1):85- 88.

[13] Xu R N, Zhai X Y. Extensions of the analytic hierarchy process in fuzzy environment[J]. Fuzzy Sets and Systems, 2002, 52: 251-257.

[14] 胡宝清.模糊理论基础(第二版)[M].湖北:武汉大学出版社,2010.

[15] 徐泽水.AHP中两类标度法的关系研究. 系统工程理论与实践,1999,19(7):97-101.

[16] 徐泽水.区间数互补判断矩阵排序的一种实用方法[J].运筹与管理,2001,10(1):16-19.

[17] Tanino T. Fuzzy preference orderings in group decision making[J]. Fuzzy Sets and Systems, 1984, 12: 117-131.

New Cognition to Multiplicative Consistency of FuzzyReciprocal Judgment Matrix

SHI Xi-jun1, ZHANG Qiang1, ZHU Ji-qiao2

(1.School of Management and Economics, Beijing Institute of Technology, Beijing 100081, China; 2.Beijing Building Materials Academy of Sciences Research, Beijing 100041, China)

To solve the problem that the relationship between addition and subtraction and that between multiplication and division in fuzzy numbers is no longer the inverse operation and make the operational laws more correspond to reality, this paper studies the multiplicative consistency of fuzzy reciprocal judgment matrix by introducing the concepts of independent variable, dependent variable, representative system and degree of freedom in classical mathematics. Then, the result reveals that it is unreasonable that if a fuzzy reciprocal judgment matrix satisfies the conditions of multiplicative consistency defined in some existing related literatures, then this matrix must be a precise reciprocal judgment matrix. Finally, based on the fuzzy cut set theory, using the relationships among elements of fuzzy reciprocal judgment matrix, the multiplicative consistency of fuzzy reciprocal judgment matrix is redefined.

management science and engineering; representative system; fuzzy theory; fuzzy number complement judgment matrix; independent fuzzy number; dependent fuzzy number

2013- 06- 06

国家自然科学基金和高等学校博士学科点专项科研基金资助(70771010，71071018， 70801064，20111101110036)

石喜军(1966-)，男，博士研究生，研究方向：模糊决策；张强(1955-)，男，教授，博士生导师，研究方向：模糊对策与决策，不确定系统理论及应用；朱吉乔(1986-)，男，硕士研究生，研究方向：管理决策理论与方法。

C934

A

1007-3221(2015)03- 0001- 05