有容量限制的可靠性固定费用选址问题
周愉峰, 马祖军, 王恪铭
(1.重庆工商大学 商务策划学校,重庆 400067; 2.西南交通大学 经济管理学院 物流与应急管理研究所,四川 成都 610031; 3.西南交通大学 峨眉校区,四川 峨眉山 614202)
有容量限制的可靠性固定费用选址问题
周愉峰1, 马祖军2, 王恪铭3
(1.重庆工商大学 商务策划学校,重庆 400067; 2.西南交通大学 经济管理学院 物流与应急管理研究所,四川 成都 610031; 3.西南交通大学 峨眉校区,四川 峨眉山 614202)
设施网络可能面临各种失灵风险,而设施选址属于战略决策问题,短期内难以改变,因而在选址设计时需要充分考虑设施的非完全可靠性。本文针对无容量限制的可靠性固定费用选址问题进行扩展,进一步考虑设施的容量约束,基于非线性混合整数规划方法建立了一个有容量限制的可靠性固定费用选址问题优化模型。针对该模型的特点,应用线性化技术进行模型转化,并设计了一种拉格朗日松弛算法予以求解。通过多组算例分析,验证了算法的性能。算例分析结果表明设施失灵风险和设施容量对于选址决策有显著影响,因而在实际的选址决策过程中有必要充分考虑设施的失灵风险及容量约束。
设施选址;设施失灵;可靠性;容量限制;拉格朗日松弛
0 引言
经典的无容量限制的固定费用选址问题(Uncapacitated fixed-charge location problem,UFLP)和P-中位问题(P-median Problem,PMP)都有一个隐含的假设:设施一旦建立,将一直运行而不失灵,即设施是完全可靠的。可事实上,由于自然灾害、罢工、所有权更替和其他因素的存在,设施失灵(Facility Disruptions,也称Facility Failures)现象时有发生。当分派设施发生失灵时,客户不得不选择距离更远的设施为其服务,这就可能导致运输成本增加,由此产生了可靠性设施选址问题。传统的选址问题通常不会改变设施网络的拓扑结构(布局),而可靠性选址问题在选址阶段考虑了失灵风险,网络的拓扑结构是可变的。由于设施选址属于战略性决策问题,短期内不会改变,因而在设计阶段就考虑失灵风险是十分重要的。而且在选址阶段考虑失灵风险可以大大降低应急成本,因而研究可靠性设施选址问题具有重要的意义。
可靠性设施选址问题最早由Snyder和Daskin[1]提出,研究如何选择低成本(传统目标函数)且可靠的设施地点。近年来,该问题引起了国外学者的关注,已成为选址研究领域的前沿性问题。通过对相关文献的分析,可以发现现有研究主要分为两类:最小期望成本模型和最坏情形成本模型。
最小期望成本模型是当前研究的重点,且主要是针对UFLP和PMP这两类经典的设施选址问题进行扩展,称为无容量限制的可靠性固定费用选址问题(Reliability Uncapacitated Fixed-charge Location Problem,RUFLP)和可靠性P-中位问题(Reliability P-median Problem,RPMP)。如Snyder和Daskin[1]对经典的UFLP和PMP进行扩展,在模型中考虑了设施失灵,首次提出了RUFLP和RPMP。他们假设所有设施具有相同的失灵概率,且考虑多级设施分派(每个客户有多个梯级后备设施),分别针对RUFLP和RPMP建立了混合整数规划模型,并设计了拉格朗日松弛(Lagrangian Relaxation,LR)算法进行模型求解。此后,针对RUFLP,Cui等[2]放宽了所有设施具有相同失灵概率这一假设,并分别建立了基于混合整数规划的离散优化模型和连续近似(Continuum Approximation,CA)模型;Lee和Chang(2007)[3]也考虑所有设施的失灵概率可以不同,但每个客户只选一个后备设施。Li和Ouyang[4]则进一步考虑了设施失灵的空间相关性。而Berman等[5],Berman等[6]则在文献[1]的基础上对RPMP做了进一步的扩展研究。
最坏情形成本模型则是在经典的选址模型基础上基于情景规划方法构建可靠性模型。Snyder等[7],Snyder和Daskin[8],Chen等[9],Church等[10],Hanley和Church[11],Peng等[12]都对最坏情形成本模型进行了相应的扩展研究。
上述有关可靠性设施选址问题的研究均未考虑设施的容量约束,但在现实生活中设施一般都有容量限制,因而放宽这一假设将使构建的模型更加切合实际。众所周知,绝大多数离散设施选址问题属于NP-hard问题,而考虑可靠性因素后问题变得更为复杂。若同时考虑容量约束,将进一步增加模型和算法的复杂性。因此,尽管有不少学者指出放宽容量约束这一假设更具现实意义,但一直未得到解决。本文针对RUFLP,在文献[2]的基础上进一步考虑设施容量限制,建立一个考虑失灵风险且有容量限制的可靠性固定费用选址问题(Reliability Capacitated Fixed-charge Location Problem,RCFLP)的离散优化模型。该模型中客户需求可以部分被满足,而RUFLP中的客户需求要么完全被满足,要么完全未被满足(当无可用设施服务该客户时)。针对该模型的特点,采用线性化技术进行转化,并设计了一种LR算法进行求解。
1 RCFLP优化模型
1.1 问题描述与假设
RUFLP研究考虑设施失灵风险条件下的设施选址及其客户分派,以寻求设施的固定开设成本、日常运行成本和期望失灵成本之和最小的选址方案。本文在此基础上进一步考虑设施容量约束,即研究RCFLP。
类似于RUFLP,考虑多级设施分派,以应对失灵风险,提高系统可靠性。对于每个客户,根据设施与其距离的远近,最多在R个梯级上各分派一个常规设施为其服务。令r表示设施分派所处的级,r=0,1,…,R-1,其中r=0表示初始设施分派,其它为后备设施分派。若客户i在第r级上被分派给了某个设施,则表明该客户在0,1,…,r-1级上也分派有后备设施,只有这前r个更近的设施都失灵后,第r级上的设施才为其服务。
由于为客户i分派的各级常规设施有可能都失灵,为此引入一个虚拟的应急设施,其固定开设成本和失灵概率均为零,且容量无限制。若客户在某一级中被分派给应急设施,则产生惩罚成本;若某一级上分派设施的容量不能完全满足客户的需求,则剩余的需求被分派给应急设施,也将产生惩罚成本。即客户的需求全部或部分未被满足时都将产生惩罚成本,该成本可理解为订单流失成本或为满足该客户需求而从竞争者处紧急采购的成本[1]。产生惩罚成本的情形包括三类:分派给该客户的所有设施都失灵(即无可用设施服务该客户);由任何一个分派设施为该客户服务的成本均超过惩罚成本;服务该客户的设施容量不足。
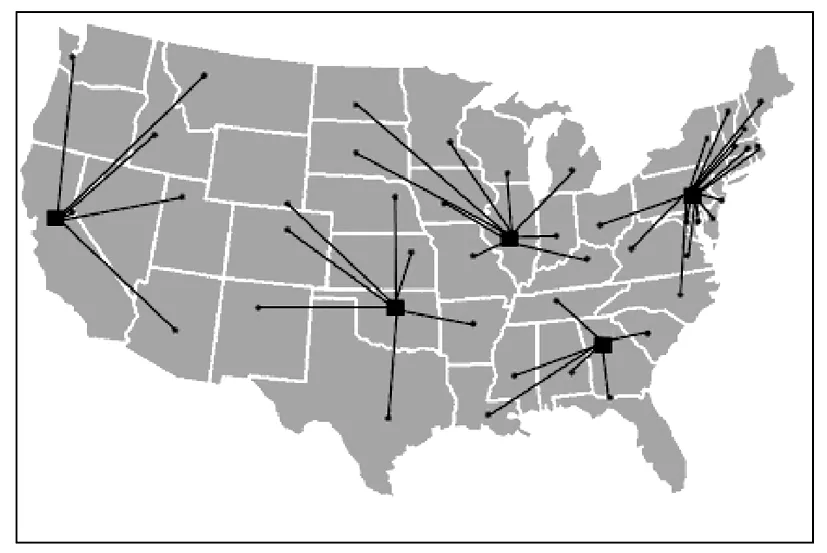
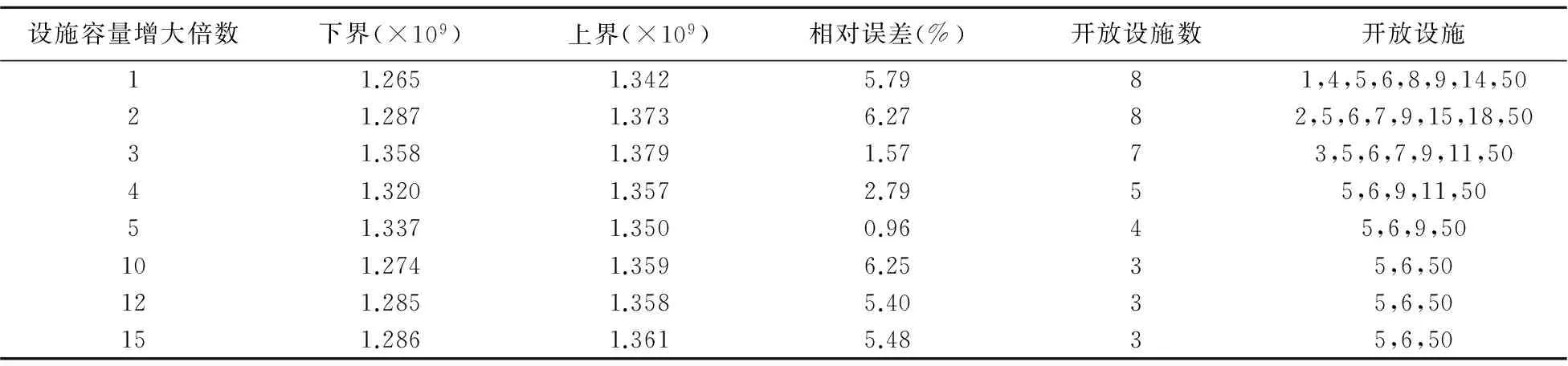
理想情况下,每个客户i恰好分派有R个常规设施,除非客户i在s(s 假设每个设施的失灵概率相互独立,且均为先验概率。客户对设施位置、设施失灵情况和设施容量状况拥有完全信息。若某一级上分派的设施失灵,客户总是搜索下一个最近的设施为其服务。需要解决的问题是:在考虑失灵风险的情况下,确定设施点的数量、位置以及客户需求在各个设施点之间的分配,目标是使固定成本、期望运输成本以及惩罚成本之和最小。 1.2 符号说明 参数: i:客户编号,i=0,1,…,I-1; j:候选设施编号,j=0,1,…,J,其中j=J表示虚拟的应急设施; hi:客户i的需求量; fj:设施j的固定开设成本,且fJ=0; vj:设施j的容量,且vJ足够大; qj:设施j的失灵概率,且0≤qj≤1,qJ=0; φi:客户i的需求未被满足时的单位需求惩罚成本; dij:设施j到客户i的单位需求运输成本,且diJ=φi; R:为每个客户最多可分派的常规设施级数,且R≥1; r:设施分派所处的级,r=0,1,…R,其中r=0为初始设施分派,r=0,1,…,R-1为后备设施分派,r=R为应急设施分派。 决策变量: Xj:在j处开设设施为1,否则为0; Yijr:设施j在r级上被分派给客户i时为1,否则为0; Pijr:由设施j在r级上服务客户i的概率; xij:设施j到客户i的运量。 1.3 模型建立 至此,可建立RCFLP的离散优化模型如下: (1) s.t.xij≤hi,∀0≤i≤I-1,0≤j≤J (2) xij=xijYijr,∀0≤i≤I-1,0≤j≤J,0≤r≤R (3) (4) (5) (6) pij0=1-qj,∀0≤i≤I-1,∀0≤j≤J (7) (8) Xj∈{0,1},∀0≤j≤J (9) Yijr∈{0,1},∀0≤i≤I-1,0≤j≤J,0≤r≤R (10) xij>0,∀0≤i≤I-1,0≤j≤J (11) 1.4 模型转化 上述模型是一个非线性混合整数规划模型,目标函数中包含三元变量xijpijrYijr和二元变量pijrYijr,约束(8)中也包含二元变量pijrYijr,使得该模型的求解很困难。在此采用Sherali和Alameddine[13]提出的线性化技术来转化该模型:引入一个新的变量Wijr来替换pijrYijr。对于任意0≤i≤I-1,0≤j≤J和0≤r≤R,为使Wijr=pijrYijr,在上述模型RCFLP中增加如下一组约束: Wijr≤pijr (12) Wijr≤Yijr (13) Wijr≥0 (14) Wijr≥pijr+Yijr-1 (15) 则模型RCFLP可转化为如下模型RCFLP’: (16) (17) (9)~(15) 模型RCFLP’的目标函数中依然含有二元变量xijWijr。令Zij=xij/hi,表示客户的需求由设施j满足的比例,有0≤Zij≤1,则xij=hiZij。由于客户i最多只可能在某一级上分派给设施j,故xij等价于xijr,则Zij等价于Zijr。因此,式(16)可改写为 再次应用线性化转换技术:令Vijr=ZijrWijr,对于任意0≤i≤I-1,0≤j≤J和0≤r≤R,在上述模型RCFLP’中增加如下一组约束: Vijr≤Zijr (18) Vijr≤Wijr (19) Vijr≥0 (20) Vijr≥Zijr+Wijr-1 (21) 则模型RCFLP’可转化成如下线性模型LRCFLP: (22) s.t. 0≤Zijr≤1,∀0≤i≤I-1,0≤j≤J,0≤r≤R (23) Zijr=ZijrYijr,∀0≤i≤I-1,0≤j≤J,0≤r≤R (24) (25) (26) (5)~(7),(9)~(15),(17)~(21) 上述混合整数线性规划模型LRCFLP可以采用CPLEX等软件包进行求解,但即使针对一个中等规模的问题也要花费很长的运算时间。为此,下面设计一种拉格朗日松弛算法来求解该模型。 用拉格朗日乘子μ松弛约束(26),得到如下目标函数: (27) 原问题可以分解成选址子问题(LSP)和客户分派子问题(ASP)。对于给定的拉格朗日乘子μ,很容易得到选址决策变量Xj的最优值: 为了计算最优的客户分派决策变量Yijr和需求分配决策变量xij,可注意到该决策问题对于每个客户是可分的[2]。对于给定的μ,客户i的分派问题(ASP)可以描述成如下的松弛子问题(Relaxed Subproblem,RSP)。为了简化,模型中省略了Yijr,pijr,Wijr,Zijr,Vijr中的下标i。 (28) s.t. 0≤Zjr≤1,∀0≤j≤J,0≤r≤R (29) (30) (31) (32) pj0=1-qj,∀0≤j≤J (33) (34) Yjr∈{0,1}∀0≤j≤J,0≤r≤R (35) (12)~(15),(18)~(21) 这是一个线性规划问题,可用传统的精确算法(如CPLEX等软件包)来求解,但问题规模较大时计算效率很低。为此,设计了如下的近似算法: Step 2 根据Yijr的值以及式(33)和(34),计算出Pijr与Wijr; Step 3 由于Vijr=ZijrWijr,可直接套用经典的线性规划算法快速求解Zijr,进而得到Vijr。 至此,可采用标准的次梯度法求解拉格朗日松弛问题,具体计算过程如下: ①初始化拉格朗日乘子μ、迭代次数n、步长θt; ②求解选址子问题; ③求解客户分派子问题; ④计算下界解:LRUFL(μ)=LSP(μ)+ASP(μ)。判断当前的拉格朗日解是否为可行解,如果当前解可行,则停止计算,该解即为LRCFLP的最优解;否则,转入⑤更新下界。 ⑤根据当前解计算次梯度和步长,并按下文的拉格朗日乘子迭代方法更新μ,若满足收敛或停止条件,则停止迭代;否则,返回步骤②。 ⑥解的可行化与上界的最终确定:下界确定后,固定Xj,Yijr,Wijr的值,在线性规划ASP问题中加入松弛的约束(26),得到问题的可行解;同时,将各个变量代回原问题中,得到问题的上界。 以文献[1]和[2]中的美国49个和88个城市节点(既是需求点,也是候选设施点)网络作为测试算例。需求hi、固定开设成本fj、惩罚成本φi的数据均从Snyder的个人主页下载(http://www.lehigh.edu/~lvs2)。设施容量vj在[40,400]内随机均匀产生;失灵概率qj在[0,0.1]内随机均匀产生。 针对49个和88个(加上虚拟的应急设施则为50个和89个)节点的网络,根据设施级数R的不同取值设计了6个不同规模的算例,计算结果和LR算法性能如表2和图1所示。可以看出,该问题上下界的相对误差最大为6.59%,最小为1.18%,计算精度在可接受范围内。结果表明,R的取值对RCFLP最优选址方案影响很小,这与文献[1]和[2]针对RUFLP的研究结论相一致。 此外,为了测试文中所提近似算法的性能,在LR算法中分别采用了3种策略求解客户分派子问题(ASP),并从求解精度和求解效率两个方面进行了对比分析(见表3)。3种策略分别为:(1)CPLEX策略:LR算法中采用CPLEX软件对ASP进行精确求解;(2)近似算法策略:LR算法中采用近似算法求解ASP;(3)混合策略:前期采用近似算法策略快速求解,后期采用CPLEX策略提高求解精度。 由表3可知,采用CPLEX策略求解49节点算例(R=2、3、4时),其精度相对于近似算法策略仅分别提高1.08%、0、1.37%,但求解时间却是后者的10倍以上,特别是随着问题规模的不断增大,求解时间也急剧增大;当问题规模扩大到88节点时,已无法在30min内求得问题的解。此外,分别在g=100、g=130、g=160(g为迭代次数)代时引入CPLEX提高精度的混合策略对LRCFLP进行求解,结果表明:与近似算法策略相比,49节点算例中引入混合策略虽能略提高计算精度,却需耗费大量的计算时间,例如R=2时,求解误差从1.08%分别缩小到0.53%、0.60%和0.91%,但求解时间却分别增加了7.49倍、6.57倍和2.59倍;而在88节点算例中,混合策略依然无法在30min内求解LRCFLP。综上所述,基于近似算法的LR启发式算法在计算效率上具有显著优势,而计算精度也在可接受范围内,因而具有良好的计算性能。 表1 拉格朗日乘子μ取不同初值的LR算法迭代次数 注:U[a,b]表示在a与b之间随机均匀产生。 表2 计算结果和LR算法性能 注:误差=(上界-下界)/上界。 以49节点算例(R=2)为例,图2给出了UFLP的最优选址-分配方案,图3给出了所有设施具有相同失灵概率时RUFLP的最优选址-分配方案,图4给出了不同设施的失灵概率不同时RUFLP的最优选址-分配方案,图5则是本文研究的设施失灵概率不同时RCFLP的最优选址-分配方案。可以看出,从不考虑设施失灵风险的选址问题到可靠性选址问题,从无容量限制的可靠性选址问题到有容量限制的可靠性选址问题,最优的选址-分配方案均发生了变化。因此,设施失灵风险与设施容量这两个因素对设施选址决策都有显著影响。 表3 采用近似算法与CPLEX分别求解ASP子问题的比较 图1 拉格朗日对偶问题的下界收敛曲线 图2 UFLP选址-分派方案[1] 图3 设施失灵概率相同时RUFLP选址-分派方案[1] 为分析设施容量对选址决策的影响,以上述49点算例(R=2)为例,以各个设施的容量为基数,再将其扩大到一定的倍数,计算结果如表4所示。可以发现,当设施容量越小时,需要设置的设施点越多,且最优选址方案不太稳定;当容量逐步扩大时,问题越来越接近于RUFLP,最优选址方案也趋于稳定。 表4 设施容量的敏感性分析 设施网络可能面临各种失灵风险,尽管失灵现象不常发生,但一旦发生,后果可能很严重。加上设施选址是一个战略性决策问题,在短期内一般不会改变,因而在在选址阶段就考虑设施失灵风险是十分必要的。为此,本文在RUFLP现有研究成果的基础上,进一步考虑设施容量限制,建立了一类RCFLP优化模型,并设计了一种LR算法进行求解。结果表明:设施容量对RCFLP选址决策有显著影响,即设施容量越小时,需要设置的设施数量越多,且最优选址方案不太稳定;设施级数R的取值对RCFLP最优选址方案没有影响。针对所建的非线性混合整数规划模型,通过线性转化技术和LR算法求解,计算效率较高。 进一步的研究可考虑非完全信息以及客户最优搜索决策行为条件下的RCFLP。此外,还可在选址与库存、路径等的集成决策问题(如定位-路径问题、定位-路径-库存问题)中考虑设施失灵风险。 [1] Snyder L V, Daskin M S. Reliability models for facility location: the expected failure cost case[J]. Transportation Science, 2005, 39(3): 400- 416. [2] Cui T, Ouyang Y, Shen Z. Reliable facility location design under the risk of disruptions[J]. Operations Research, 2010, 58(4): 998-1011. [3] Lee S D, Chang W. On solving the discrete location problems when the facilities are prone to failure[J]. Applied Mathematical Modeling, 2007, 31(5): 817- 831. [4] Li X, Ouyang Y. A continuum approximation approach to reliable facility location design under correlated probabilistic disruptions[J]. Transportation Research Part B: Methodological, 2010, 44(4): 535-548. [5] Berman O, Krass D, Menezes M. Facility reliability issues in network p-median problems: strategic centralization and co-location effects[J]. Operations Research, 2007, 55(2): 332-350. [6] Berman O, Krass D, Menezes M. Locating facilities in the presence of disruptions and incomplete information[J]. Decision Sciences, 2009, 40(4): 845- 868. [7] Snyder L V, Caparra M, Daskin M S. Planning for disruptions in supply chain networks[J]. Operations Research, 2006, 25(10): 234-259. [8] Snyder L V, Daskin M S. Models for reliable supply chain network design. In Murray A, Grubesic T H. (Ed), Reliability and Vulnerability in Critical Infrastructure: A Quantitative Geographic Perspective[M]. Springer, New York, 2006. [9] Chen G, Daskin M S, Shen Z. The -reliable mean-excess regret model for stochastic facility location modeling[J]. Naval Research Logistics, 2006, 53(7): 617- 626. [10] Church R L, Scaparra M P, Hanley J. Optimizing passive protection in facility systems[R]. Working paper, Isoldex, Spain, 2006. [11] Hanley J, Church R L. Planning for facility-loss: a bilevel decomposition algorithm for the maximum covering location-interdiction problem[R]. Working paper, Oxford University, Oxford, England, 2005. [12] Peng P, Snyder L V, Lim A, et al. Reliable logistics networks design with facility disruptions[J]. Transportation Research Part B: Methodological, 2011, 45(8): 1190-1211. [13] Sherali H D, A Alameddine. A new reformulation-linearization technique for bilinear programming problems[J]. Global Optimization, 1992, 2(4): 379- 410. [14] Fisher M L. The Lagrangian relaxation method for solving integer programming problems[J]. Management Science, 1981, 27(1): 1-18. [15] Lim C, Sherali H D. Convergence and computational analyses for some variable target value and sub-gradient deflection methods[J]. Computational Optimization and Applications, 2006, 34(3): 409- 428. Reliability Capacitated Fixed-charge Location Problem ZHOU Yu-feng1, MA Zu-jun2, WANG Ke-ming3 (1.School of Business Planning, Chongqing Technology and Business University, Chongqing 400067, China; 2.Institute for Logistics and Emergency Management, School of Economics and Management, Southwest Jiaotong University, Chengdu 610031, China; 3.Emei Campus, Southwest Jiaotong University, Emeishan 614202, China) Infrastructure networks have the risk of disruptions. Because facility location is a strategic decision that can not be changed in a short time, it is critical to account for the non-complete reliability of facility in designing the network. The classical reliability uncapacitated fixed-charge location problem is extended by considering the capacity constraint. And the reliability capacitated fixed-charge location problem under the risk of disruptions is formulated as a mixed integer nonlinear programming model. Considering the characteristics of the model, a linearization technique is applied to convert the model and a lagrangian relaxation algorithm is developed to solve the problem. A numerical example is given to verify the model and algorithm performance. The results show that facility capacity has a notable impact on location decision, and the unexpected failures of facility and capacity constraint of facility should be fully considered in real-life location decision process. facility location; facility disruptions; reliability; capacitated; Lagrangian relaxation 2012-12-16 国家自然科学基金项目(90924012,71090402,71271227);教育部新世纪优秀人才支持计划资助项目(NCET-10- 0706);四川省哲学社会科学研究规划项目(SC11B049);四川省学术和技术带头人培养资金项目(川人社办发[2011]441号);中央高校基本科研业务费专项资金资助项目(SWJTU11CX152,2682013CX073) 周愉峰(1984-),男,湖南双峰人,讲师,博士,研究方向:应急物流、物流系统优化;马祖军(1974-),男,浙江开化人,教授,博士生导师,研究方向:物流与供应链管理、应急管理、产品回收管理。 C931;O221 A 1007-3221(2015)03- 0006- 08




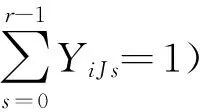






2 模型求解








3 算例研究






4 结论

