基于传染病模型的集群内异质企业间知识传播机理分析与仿真
胡绪华, 陈丽珍, 吕 魁
(1.江苏大学 财经学院,江苏 镇江 212013; 2.南京审计学院 审计信息工程重点实验室,江苏 南京 210029)
基于传染病模型的集群内异质企业间知识传播机理分析与仿真
胡绪华1, 陈丽珍1, 吕 魁2
(1.江苏大学 财经学院,江苏 镇江 212013; 2.南京审计学院 审计信息工程重点实验室,江苏 南京 210029)
知识传播是产业集群内知识资源动态累积的过程,是新时期产业集群竞争优势的重要源泉之一。本文根据企业规模及其在产业集群内地位的差异将集群企业划分大小两类异质企业,构建了基于传染病模型的产业集群内异质企业间的知识传播模型,通过模型分析推导出了知识传播再生数的一般表达式,验证了知识传播平衡点的存在性与稳定性。进一步结合仿真分析发现,企业间接触率、学习成功率、大小企业比例均会影响到知识传播的再生率,进而影响集群知识传播的平衡点,且在知识传播再生数大于1的情况下,随着集群内大企业占比的上升,知识传播再生数将相应下降,集群内知识交流氛围的活跃性也将下降。
产业集群;知识传播;传染病模型;仿真
0 引言
产业集群是特定产业中相互联系的公司或机构聚集在特定地理位置的一种现象,既包括了零件、设备、服务等特殊原料品的供应商和特殊基础建设的提供者,也包括了政府和其他机构——像大学、制定标准的机构、职业训练中心以及贸易组织等[1]。作为一种介于市场与科层组织之间的产业组织形态,产业集群具有比市场稳定比科层组织灵活的特征,已经成为国内外区域经济发展的重要模式,其竞争优势也已成为国家或地区竞争力的主要源泉。伴随着知识经济时代的到来,产业集群的优势资源已经由传统的物质资源转变为集群内的知识资源,而且知识资源会在集群内不同个体之间传播、转化、创新,形成SECI知识螺旋[2]。其中,知识传播作为集群内知识资本的动态累积过程,不仅决定着集群知识资本量的累积,更是决定了集群知识资本质的提升。关于产业集群内知识传播的研究已经引起了国内外理论研究者和政府政策制定者的普遍关注,并成为产业集群研究的一个重要分支领域。相关领域的部分学者结合各自学术背景从客户关系[3,4]、组织相近性和认知性[5,6]等角度开展了系列研究。在知识传播模型的构建中,包括知识场模型[7]、微分动力学模型[8]、变分不等式理论[9]等在内的一些复杂工具被应用进来。
产业集群发展具有生态性特征[10],这为我们开辟了采用传染病模型研究产业集群知识传播的可行性。Kermack和McKendrick构造了著名的SIR仓室传染病模型,并用于研究伦敦黑死病流行的规律和1906年孟买的瘟疫[11],奠定了传染病动力学的研究基础。部分学者已经尝试采用传染病模型研究知识传播问题。王秀红等人比较了隐性知识传播过程和传染病传播过程的相似性, 阐述了用传染病模型研究隐性知识传播机制的可行性[12];李勇等人基于复杂网络上传染模型研究的新进展,在分类混合假设条件下,验证了知识传播动力学结构的层次性[13]。已有的研究成果奠定了本文采用传染病模型研究集群内知识传播的方法论基础。
另外,集群内企业经济地位的差异性也会影响集群企业间的知识传播过程。由于专业化分工的存在,集群内领导企业需要有效协调与其他企业的生产关系才能获得竞争优势,因此领导企业需要对知识进行编码后向其他关联企业传播,同时为防止该知识被外部竞争者模仿,领导企业还会采用适当控制性策略[14]。集群内的领导企业又在一定程度上承担了集群知识传播系统中守门人的角色[15]。可见,集群企业经济地位的差异性对集群知识传播的影响不可忽视。从目前掌握的文献来看,关于知识传播和产业集群知识系统的研究已经取得了比较丰硕的成果,但从企业异质的角度探讨集群企业间知识传播的研究尚不多见。
本文根据集群企业规模和企业在产业集群内地位的差异将产业集群内的企业划分为大小两类企业[16],大企业在产业集群内处于主导和支配地位,小企业因规模较小实力较弱而环绕在大企业周边[17],探讨这种产业集群结构中知识传播的机理问题。如,上海汽车产业集群就是由上海大众、上海通用和上海通用五菱等大型整车企业及江森自控、博世、伟世通、德尔福等一大批外国零配件制造商和国内零配件制造商构成。由于集群企业间知识传播与病毒在生物群体内的传播具有很强的类同性,本文将借用传染病模型的分析思路,构建基于传染病模型的产业集群内异质企业间知识传播的机理模型,并进行系统仿真,以理论推导和系统仿真交互验证的方式深度刻画各特征变量在产业集群知识传播系统中的作用机理。
1 模型建立
在对产业集群内异质企业间知识传播过程与病毒在生物群体内传播过程比较分析的基础上,归纳出集群内知识传播系统的特征要素并给出相应的假设条件,进而借用传染病模型的研究思路,构建基于传染病模型的一种知识在产业集群内异质企业间传播的机理模型,推演其平衡点的一般表达式。
1.1 模型假设
传染病模型的研究和应用已经成为数学知识应用的一个重要领域[18]。结合产业集群内异质企业间知识传播的基本特征,本文给出以下几点假设。
(1)根据产业集群内企业对知识的掌握情况,将集群企业分为三类:缺乏知识的企业S(未掌握知识,且时刻准备学习新知识的企业),掌握知识的企业I(已掌握知识,并将其运用于生产经营活动中,是现有知识的传播源),升级知识的企业R(放弃现有知识,已转向了更高层次的知识,对现有知识传播不再产生影响)。在此将S分为两组,S1代表大企业群,S2代表小企业群。这样可得N≡S1+S2+I+R。
(2)产业集群是个相对开放的产业系统,不仅有新企业持续进入该行业,也有企业因其他原因转型而退出原行业,企业的进入与退出主要受行业利润与企业经营能力影响,因此即使拥有某项知识,该企业也可能因转型而退出原行业,放弃原知识。为了表现知识传播的这种特点,在模型中假设集群知识传播系统中的三类企业均有可能发生转型而退出当前的知识传播系统。假定新企业进入系数与老企业转型退出系数相等,均为b,其中大企业单位时间内进入的数量为pbN,小企业单位时间内进入的数量为(1-p)bN;此时,未掌握知识的大企业单位时间内退出数量为bS1,未掌握知识的小企业单位时间内退出数量为bS2,掌握知识的企业退出数量为bI,升级知识的企业退出数量为bR。产业集群内企业总数保持为一常数N。
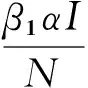
(4)t时刻,单位时间内I类企业知识升级(转化为R类企业)的数量与I类企业自身数量成正比,比例系数为γ,本文将其称为知识升级系数,从而单位时间内I类企业知识升级到R类企业的数量为γI。
(5)企业一旦升级为R类企业(转向更高层次的知识),即进入新一轮知识的传播系统,退出现有知识的传播系统,失去对现有知识的传播能力。
1.2 模型构建
根据以上假设,产业集群知识系统内两类企业间的知识传播过程可以用如下的框图描述(见图1)。
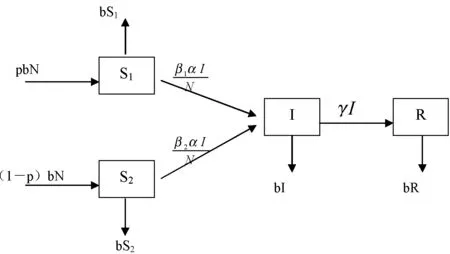
图1 产业集群知识系统内两类企业间的知识传播框架图
根据图1的描述,参照文献[20],在此建立相应的DS-I-A模型:
(1)
本文讨论的是产业集群内两类企业间的知识传播问题,具有知识传播属性的企业(I类企业)和具有被传播属性的企业(S1、S2类企业)是考察的重点,因此本文在此将除去最后一个方程,形成新的模型(2),参照文献[21,22]的研究思路,来考察模型(2)的稳定性和阈值。
(2)
其中(S1,S2,I)∈G={(S1,S2,I)|0≤S1≤N,0≤S2≤N,0≤I≤N,S1+S2+I≤N}。
2 模型分析
为求模型(2)的平衡点,令其右端为0,得模型(3):
(3)
下面就I=0和I≠0两种情况进行讨论:
2.1 知识传播再生数的求解
在生物传染病模型中,基本再生数是指一个病原体在平均患病期内所传染的人数[23]。本文所讨论的知识传播再生数是指,一个掌握知识的企业(I类企业)在一个周期内能够将知识成功传播给未掌握知识的企业(S类企业)数量。知识传播再生数R0的大小直接影响系统的平衡状态,当R0<1时平衡点E0渐进稳定,当R0>1时平衡点E0不稳定。若产业集群知识系统要步入无知识传播平衡状态,掌握并运用知识的企业数量将趋向于为0(即I=0),最终,知识传播系统进入无知识传播的状态,两类知识缺失的企业数量均为正。由模型(3)可求得无知识传播的平衡点为E0(S1=pN,S1=N-pN,I=0)。
下面将通过考察E0的稳定性来推导产业集群知识系统内知识传播再生数R0。
模型(2)在E0点的Jacobian为:
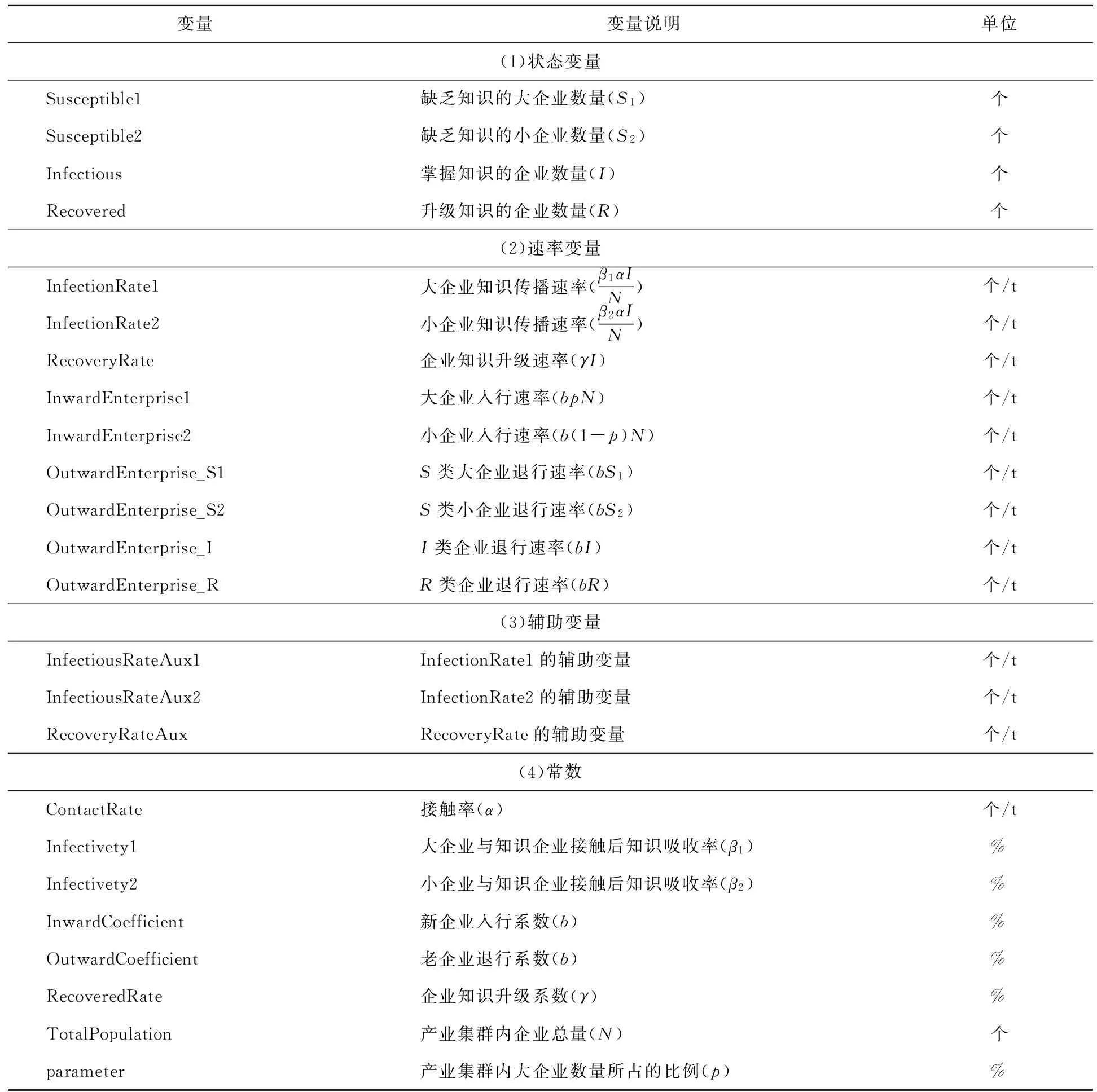
显然,只要 -(γ+b)+β1αp+β2α(1-p)<0,则J的所有特征值均为负。这样就可以将产业集群知识系统中知识传播再生数R0定义为:
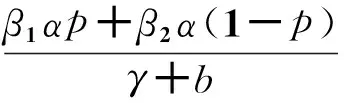
将R0对p求一阶偏导可得
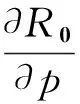
由此可以判定R0关于变量p的函数单调递减。
结论1 在拥有两类企业的产业集群知识传播模型中,大企业的知识学习成功率通常小于小企业(β1<β2),这将导致随着产业集群内大企业数量比例的上升,知识传播再生数将逐步下降,知识交流的活跃性也将下降。
2.2 无知识传播平衡点与稳定性
下面进一步证明当R0<1时,无知识传播平衡点E0的稳定性。
由模型(2)前两个方程可得:
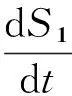
由此可得:
S1(t)≤pN+S1(0)e-bt,S2(t)≤(1-p)N+S2(0)e-bt
由模型(2)的第三个方程可得:
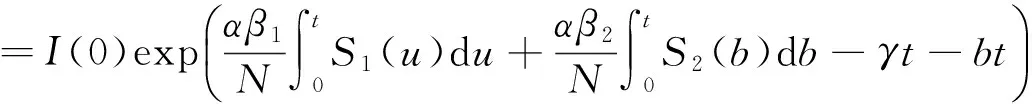
由此可见,当t→∞和R0<1条件满足时,I(t)将趋向于0。根据上文对稳定点E0的定义,对E0渐进稳定性的验证可以转化为对(S1=pN,S1=N-pN)在区间Ω上的渐进稳定性的检验。其中Ω={(S1,S2)|0≤S1≤N,0≤S2≤N,I=0}。
在区间Ω内,模型(2)的前两个方程可以转化为方程组(4):
(4)
求解方程组(4)可得结果:
(5)
从式(5)中可以看出,当t→∞时,S1(t)和S2(t)分别趋向于pN和(1-p)N。
结论2 在拥有两类企业的产业集群知识系统内,在知识传播再生数R0确定后,当R0<1时,该产业集群知识系统的无知识传播平衡点E0(S1=pN,S1=N-pN,I=0)将渐进稳定。
2.3 有知识传播平衡点与稳定性
下面将讨论R0>1时模型(1)的平衡点和稳定性。在此分两步进行,首先讨论存在知识传播的平衡点的存在性和唯一性,其次讨论这一平衡点的稳定性。
第一步,平衡点的存在性和唯一性的讨论
由模型(1)的前两个方程可得:
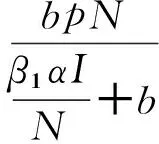
(6)
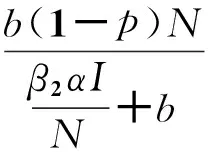
(7)
将式(6)和(7)带入模型(3)的第三个方程,可以得到:
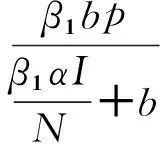
(8)
由此可得,只有当式(8)存在一个正的I值时,模型(1)才会存在有知识传播的平衡点。
假设式(8)的左边为函数:
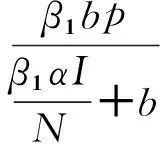
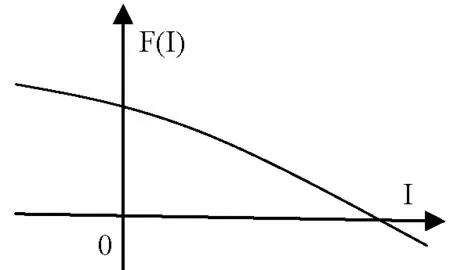
图2 函数F(I)
F(I)的函数曲线图如图2所示,对F(I)求导可得:
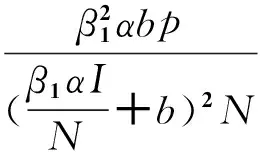
显然F′(I)<0,因此可以断定函数F(I)是单调递减。而且对F(I)取极限可得:
由此可以得到,只有当F(0)>0时,式(8)的I才会存在正解。
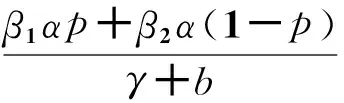
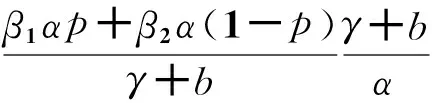
由此可以证明,当R0>1时模型(1)的存在知识传播的平衡点存在而且唯一。
第二步,平衡点稳定性的讨论
令E*(S1*、S2*、I*)是产业集群知识系统中唯一的知识传播平衡点,进一步做如下假设:
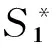
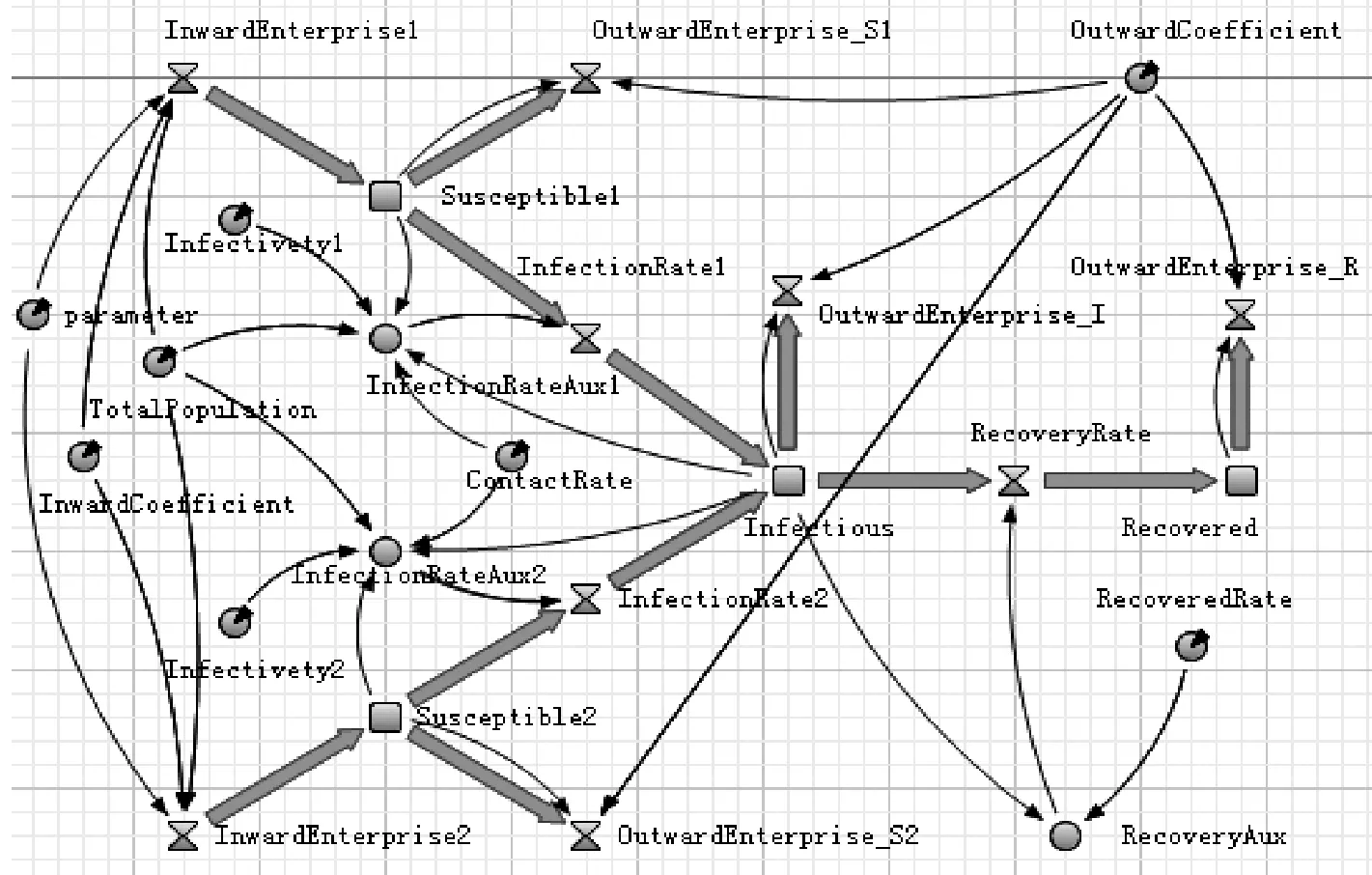
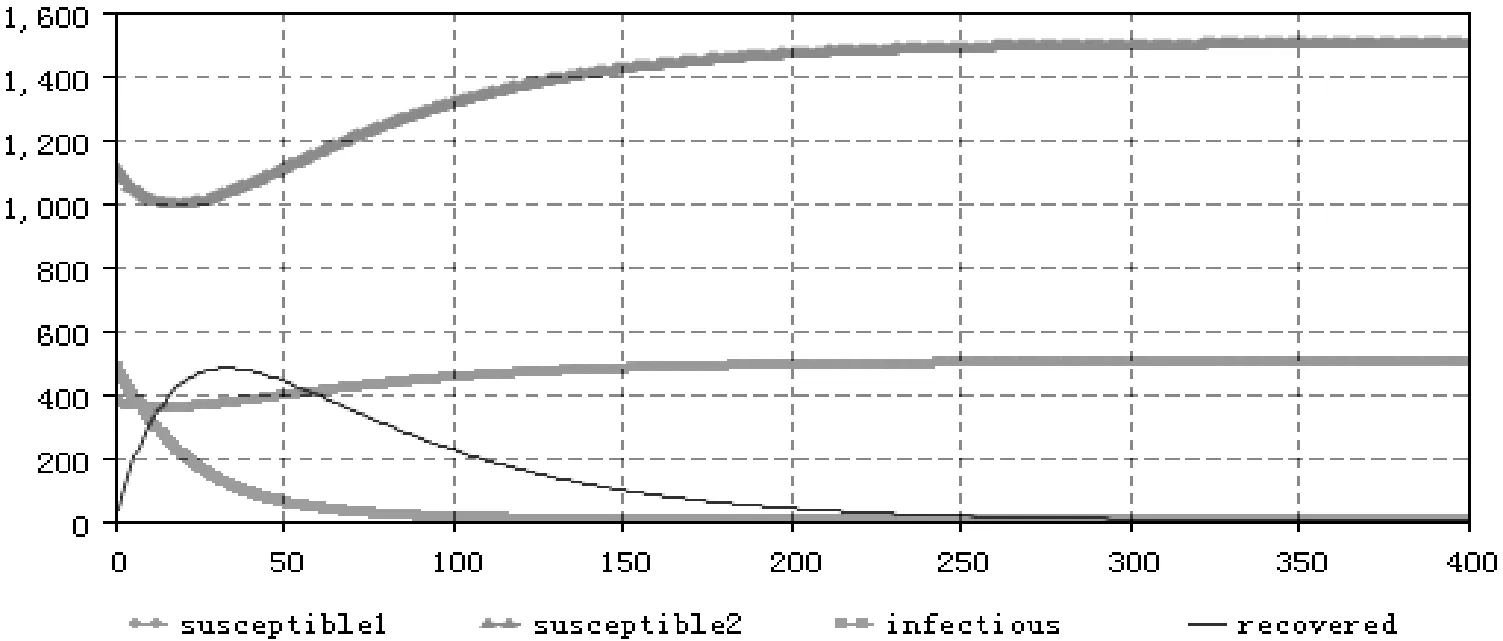
其中-1 (9) 模型(9)与模型(2)显然具有相同的稳定性。 在常微分方程中讨论平衡点的稳定性时通常的方法是构造一个无限大的正定Liapunov函数,使其沿系统轨迹线的全导数在所讨论的区域内是负定的,则相应平衡点在所讨论区域内是全局渐近稳定的。 在此,构造Liapunov函数: 由此可得除(x1,x2,y)=(0,0,0)时,V等于0外,V均为正。 沿模型(9)的轨迹求V对t的全导数,可得: 结论3 在拥有两类企业的产业集群知识系统内,在知识传播再生数R0确定后,当R0>1时,该产业集群知识系统存在唯一的有知识传播平衡点E0*,而且该平衡点全局渐进稳定。 3.1 系统动力学模型的构建 将系统(1)中的参变量进行设计,转换成系统动力学的语言变量,借用anylogic系统动力学分析软件构建产业集群内异质企业间的知识传播的系统动力学模型,形成流图(结构图)如图3所示,对产业集群内异质企业间知识传播的系统动力学模型的主要变量描述见表1所示。 图3 产业集群知识系统内两类企业间知识传播的系统动力学模型流图 变量变量说明单位(1)状态变量Susceptible1缺乏知识的大企业数量(S1)个Susceptible2缺乏知识的小企业数量(S2)个Infectious掌握知识的企业数量(I)个Recovered升级知识的企业数量(R)个(2)速率变量InfectionRate1大企业知识传播速率(β1αIN)个/tInfectionRate2小企业知识传播速率(β2αIN)个/tRecoveryRate企业知识升级速率(γI)个/tInwardEnterprise1大企业入行速率(bpN)个/tInwardEnterprise2小企业入行速率(b(1-p)N)个/tOutwardEnterprise_S1S类大企业退行速率(bS1)个/tOutwardEnterprise_S2S类小企业退行速率(bS2)个/tOutwardEnterprise_II类企业退行速率(bI)个/tOutwardEnterprise_RR类企业退行速率(bR)个/t(3)辅助变量InfectiousRateAux1InfectionRate1的辅助变量个/tInfectiousRateAux2InfectionRate2的辅助变量个/tRecoveryRateAuxRecoveryRate的辅助变量个/t(4)常数ContactRate接触率(α)个/tInfectivety1大企业与知识企业接触后知识吸收率(β1)%Infectivety2小企业与知识企业接触后知识吸收率(β2)%InwardCoefficient新企业入行系数(b)%OutwardCoefficient老企业退行系数(b)%RecoveredRate企业知识升级系数(γ)%TotalPopulation产业集群内企业总量(N)个parameter产业集群内大企业数量所占的比例(p)% 3.2 参数的设定与仿真 按照产业集群内异质企业间知识传播的系统动力学模型流图的思路,对系统动力学模型中数值假定的基础上仿真,以验证本节讨论所获得的结论1、结论2和结论3。 (1)仿真实验一 产业集群内企业数量设定为2000个,其中大企业所占比例parameter为0.25,单位时间设定为天,在初始状态产业集群内有500家企业掌握并运用知识(大企业125家,小企业375家),成为知识传染源。进一步假设Infectivety1(β1)为0.12,Infectivety2(β2)为0.18,ContactRate(α)为0.5个/天,InwardCoefficient和OutwardCoefficient(b)为0.02,RecoveredRate(γ)为0.08。此时 将数值带入系统动力学模型按照流图3的思路仿真,结果如图4所示。 图4 R0<1时产业集群内两类企业间知识传播仿真图 图5 R0>1时产业集群知识系统内两类企业间知识传播仿真图 从图4中可以看出,在知识传播再生率小于1的情况下,虽然初始状态产业集群内存在500个知识传播源,到第300天左右的时候掌握知识的企业和知识升级的企业数量均趋向于零,而缺乏知识的大企业数量趋向于500,缺乏知识的小企业数量趋向于1500,这与结论2讨论的内容基本一致。在仿真实验一模拟的情景下,单位时间内I类企业因转型退出当前知识传播系统的数量与向R类企业转换的数量的和大于S类企业向I类企业转换的数量,导致I类企业的数量越来越少,直至为零。在现实产业集群系统中,也经常可以观察到这一现象,产业集群内企业间虽然在一定阶段内存在知识传播,但同时集群内企业还会按照一定的速率向其他行业转型,离开现有的知识传播系统,当集群内企业转型速度相对较快时,整个集群将面临转型,原有知识的传播系统因再生率小于1而难以为继,知识传播现象最终消失。 (2)仿真实验二 仍然将产业集群内企业数量设定为2000个,其中大企业所占比例parameter为0.25,单位时间设定为天,在初始状态产业集群内有500家企业掌握并运用知识(大企业125家,小企业375家)。进一步假设Infectivety1(β1)为0.22,Infectivety2(β2)为0.36,ContactRate(α)为0.5个/天,InwardCoefficient和OutwardCoefficient(b)为0.02,RecoveredRate(γ)为0.08。此时 将数值带入后,仿真模拟结果如图5所示。 从图5中可以看出,在知识传播再生率大于1的情况下,到第300天左右的时候,产业集群知识系统内的知识传播活动趋于动态稳定,知识缺乏的大企业数量维持在350左右,知识缺乏的小企业数量维持在895左右,掌握并运用知识的企业数量维持在150左右,处于知识升级状态的企业数量维持在605左右。这与结论3讨论的内容基本一致。 (3)仿真实验三 考察产业集群内大企业数量所占比例的变化对知识传播平衡点的影响。在仿真实验一的假设基础上,将parameter的值修订为0.75。此时 将数值带入后仿真系统,模拟结果如图6所示。从图6可以看出,从第200天开始系统趋于渐近稳定,此时掌握并运用知识的企业和知识升级的企业数量均为0,产业集群内无知识传播行为的发生。 同样在仿真实验二的假设基础上,将parameter的值也修订为0.75。此时 将数值带入后仿真系统,模拟结果如图7所示。从图7可以看出,从第250天开始系统趋于渐近稳定,产业集群内掌握并运用知识的企业只维持在83左右的水平,处于知识升级状态的企业数量也只有330左右,说明此时产业集群内企业相互之间比较封闭,知识传播活动并不活跃。 图6 R0<1且p值增加到0.75时仿真图 图7 R0>1且p值增加到0.75时仿真图 将仿真图4与图6相比较,不难发现虽然最后系统趋于稳定后均不再存在知识传播行为的发生,但当产业集群内大企业数量所占的比例从0.25上升到0.75后,知识传播再生数R0下降,后者产业集群知识传播系统提前进入无知识传播平衡态。同样将仿真图5与图7相比较,也可以发现当p值上升后,R0下降,产业集群知识传播系统不仅提前进入知识传播平衡态,而且掌握并运用知识的企业数量也从150下降到83。这与结论1讨论的内容基本一致。 在产业集群异质企业间的知识传播系统中,知识传播再生数R0是决定知识传播平衡状态的关键要素。当R0<1时,无论起始状态有多少知识源,最终系统将进入无知识传播的平衡状态;而当R0>1时,系统将进入一个有知识传播的动态平衡状态。 从本文推导出的知识传播再生数R0的一般表达式中可以发现,企业进入与退出比率b、企业知识升级系数r与知识传播再生数R0呈反比;而企业间接触率α、知识学习成功率(β1和β2)与知识传播再生数R0呈正比。政府、中介组织、集群企业等可以通过举办知识交流活动提高企业接触率和学习成功率,进而提高知识传播再生数R0。 另外,在产业集群内若大企业占比p越高,则知识传播再生数R0越小,产业集群内知识传播的氛围也更呆板。究其原因,主要是因为大企业和小企业因为自身知识能力和生存压力的不同,学习新知识的动力也不尽相同。通常小企业在知识学习方面要更积极活跃(即β1<β2),而大型企业因为自身升级的成本、未知风险和预期的收益,将拒绝接受新知识或者充当了知识守门人的角色。因此,当一个产业集群主要由大型企业组成时,此时产业集群内企业间的知识交流活动将变得懒散;而当一个产业集群主要由小型企业组成时,基于自身生存的压力和知识匮乏的现状,它们对专业知识的追逐直接促进了企业间的知识交流,无形中充当起了产业集群内知识传播的媒介角色,此类产业集群内企业间的知识交流活动也将变得更加活跃。 [1] Michael E Porter. Clusters and the new economics of competition[J]. Harvard Business Review, 1998, 76(6): 77-90. [2] Nonaka I. A dynamic theory of organizational knowledge creation[J]. Ogranization Science, 1994, 5(1): 14-37. [3] 梁晶,吴江宁.面向客户需求的企业集群知识传播模型与仿真[J].运筹与管理,2010,19(4):150-153. [4] Kishimoto C. Upgrading in the taiwanese computer cluster: transformation of its production and knowledge systems[M]. Institute of Development Studies, 2003. [5] 李琰,杨勇,钟念,黄超.基于知识传播的集群聚集能力系统动力学研究[J].系统管理学报,2011,20(1):94-97. [6] Malmberg A, Maskell P. The elusive concept of localization economies: towards a knowledge-based theory of spatial clustering[J]. Environment and planning A, 2002, 34(3): 429- 450. [7] 陈娟,芮明杰.高技术企业知识员工间的知识传播模型[J].研究与发展管理,2004,16(5):46-52. [8] 张生太,李涛,段兴民.组织内部隐性知识传播模型研究[J].科研管理,2004,25(4):28-32. [9] 沈秋英,王文平.基于社会网络与知识传播网络互动的集群超网络模型[J].东南大学学报(自然科学版),2009,39(2):413- 418. [10] 周晔,胡汉辉.地方主导产业的演化规律与产业集群生态特征初探——兼论产业集群与企业集聚的区别[J].中国软科学,2007,(7):147-151. [11] Kermark M D, Mokendrick A G. Contributions to the mathematical theory of epidemics[J]. Part I, Proc Roy Soc A, 1927, 115(5): 700-721. [12] 李勇,史占中,屠梅曾.企业集群中的创新传播动力学研究[J].科学学与科学技术管理,2005,(5):77- 80. [13] 王秀红,韩琼,韩光平.员工隐性知识传播的系统动力学模型研究[J].情报杂志,2008,(3):57- 60. [14] Feldman M P. Location and innovation: the new economic geography of innovation, spillovers, and agglomeration, see in the Oxford Handbook of economic geography[M], Clark G L, Feldman M P, Gertler M S, Editors. Oxford: Oxford University Press, 2000: 373-394. [15] Morrison A. Gatekeepers of knowledge within industrial districts: who they are, how they interact[J]. Regional Studies, 2008, 42(6): 817- 835. [16] 胡绪华,吕魁.基于集群企业博弈分析的知识再创造主体选择研究[J].电子科技大学学报,2010,12(2):17-22. [17] Markusen. Sticky places in slippery spaces: a typology of industial Districts[J]. Economic Geography, 1996, 72(3): 293-313. [18] 刘应麟.传染病学[M].北京:人民卫生出版社,1997. [19] Olson, Mancur. The logic of collective action; public goods and the theory of groups[M], Harvard University Press, 1971. [20] Hyman J, Li J. An intuitive formulation for the reproductive number for the spread of disease in heterogeneous populations[J]. Math Biosci. 2000, 167(1): 65- 86. [21] Castillo-Chavez C, Huang W, Li J. Competitive exclusion in gonorrhea models and other sexually transmitted diseases[J]. SIAM Journal on Applied Mathematics, 1996, 56(2): 494-508. [22] James M, Hyman Jia Li. Differential susceptibility epidemic models[J]. Mathematical Biology, 2005, 50(6): 626- 644. [23] 马知恩,周义仓.传染病动力学的数学建模与研究[M].北京:科学出版社,2004. Analysis and Simulation of the Knowledge Diffusion Mechanism withinIndustrial Clusters Based on Epidemic Model HU Xu-hua1, CHEN Li-zhen1, LV Kui2 (1.School of Finance & Economics, Jiangsu University, Zhenjiang 212013, China; 2.Key Lab of Audit Information Engineering, Nanjing Audit University, Nanjing 210029, China) A model is analyzed to reveal the knowledge diffusion mechanism of the industry cluster based on epidemic model. Knowledge is the main resource of the competitive advantage of industry clusters. It is assumed that there are two kinds of enterprises(the big enterprises and the small enterprises)within the clusters. After a systematic review of the literature, a knowledge diffusion mechanism of the industry clusters is structured. The general expression of the reproductive number is calculated, and the existence and stabilization of the knowledge diffusion equilibrium are verified. With the theoretical derivation and simulation, it is revealed that the contact rate, learning success rate and proportion of the two kinds of enterprises will influence the knowledge diffusion reproductive number and the equilibrium point. The knowledge diffusion reproductive number is reduced with the increase of the large enterprise proportion, so is the activeness of knowledge communication in industrial clusters. industrial clusters; knowledge diffusion; epidemic model; simulation 2013- 04-28 国家自然科学基金资助项目(71203079);国家自然科学基金资助项目(70973045);江苏省高校哲学社会科学基金(2010SJB79005);江苏大学人文社科基金(10JDG155) 胡绪华(1978-),男,江苏连云港人,江苏大学副教授、博士,研究方向:产业集群知识管理;陈丽珍(1956-),女,湖北武汉人,江苏大学教授、博士生导师,研究方向:经济系统分析;吕魁(1974-),男,河南商丘人,南京审计学院副研究员、博士,研究方向:产业组织理论。 F062 A 1007-3221(2015)03- 0248-10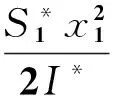
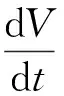

3 数值仿真
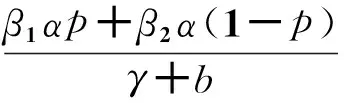

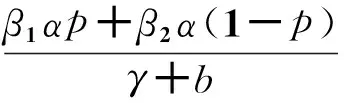
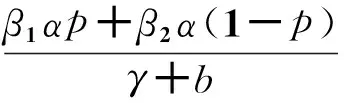
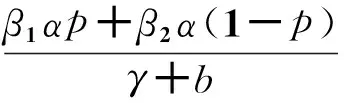
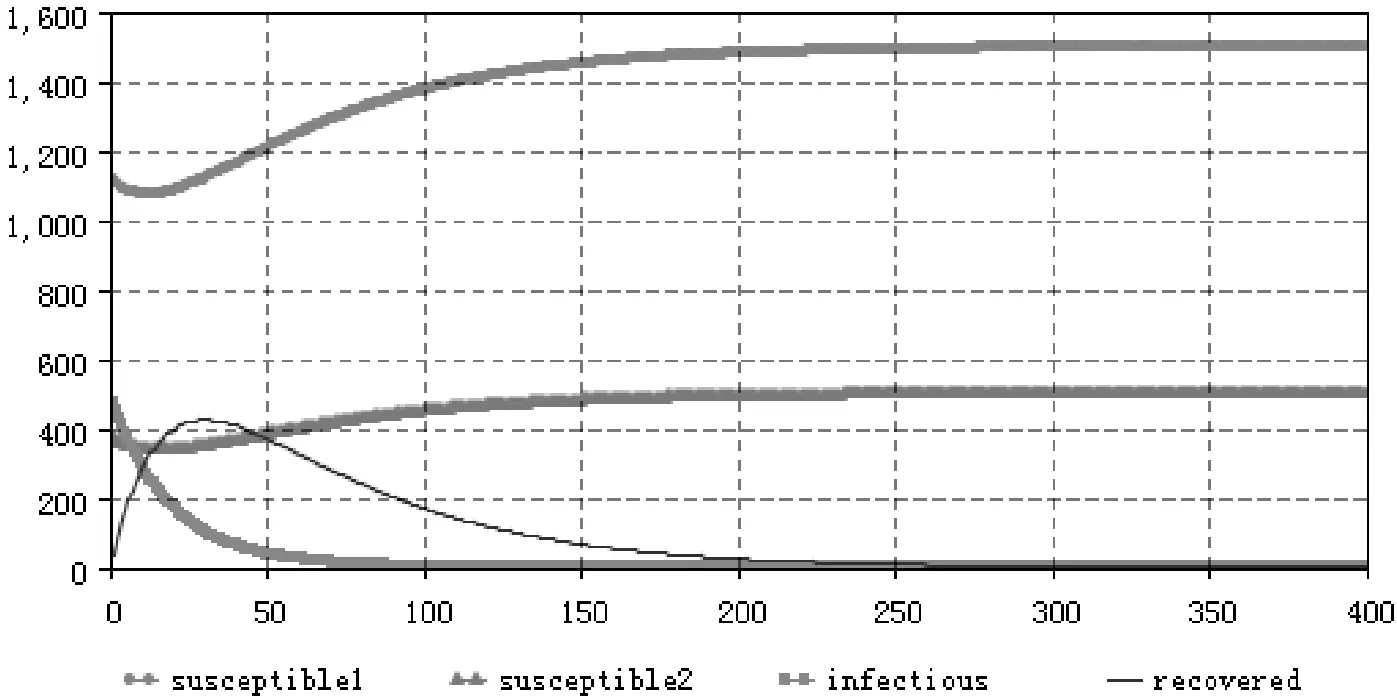
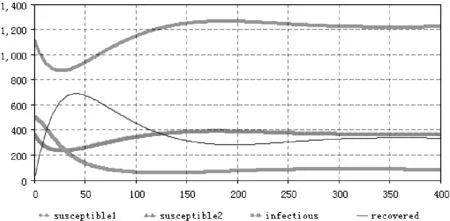
4 结论

