水面浮式稳定平台模态分析与结构优化
姚宗辰,张 合
(南京理工大学 机械工程学院,南京 210094)
0 引言
无论在军事上还是在民用中稳定平台都有着重要的用途。稳定平台能够使负载设备相对于某惯性空间保持水平稳定,确保安装于稳定平台上的装置在工作时不会受载体的运动影响[1]。
振动是制约稳定平台工作精度与可靠性的主要因素之一。一方面,系统的振动极大的影响了陀螺仪采样数据的精度,导致控制系统性能不能充分发挥;另一方面,传动链的振动及来自外界的激励会引发系统共振,可导致调平电机卡死、稳定平台失控的情况。为减小振动和谐振对控制系统性能及平台动态性能的影响,不仅需要对控制算法进行优化,利用软件抑振,而且需要进行结构优化[2,3]。
本文以工作于水面的浮式稳定平台为研究对象,从平台关键结构设计方面入手,对稳定平台关键结构进行模态分析,以避免共振现象的发生。本文首先针对稳定平台的整体结构建立有限元模型,再利用ANSYS Workbench对稳定平台整体结构进行模态分析,将得到的前六阶模态与稳定平台实际工作环境相结合,分析结构刚度中存在的薄弱环节,最后提出优化方案并进行仿真验证。本文的工作对该平台结构优化设计与分析、控制技术改进均有指导意义,并为该平台进一步的动力学分析奠定基础。
1 有限元模型的建立
该稳定平台主要由动平台、虎克铰、定平台、推杆、滚珠丝杠、传动机构与驱动电机组成,如图1所示。

图1 水面浮式稳定平台结构简图
由于稳定平台结构复杂且零件较多,存在大量微小特征,大大增加了单元数量,影响计算速度。因此,在保证计算精度的前提下,为了提高计算速度,减小资源占用,需在进行有限元分析前对倒角、螺栓连接孔和定位销等非重要零件的微小特征进行适当的简化处理[4]。此外,由于定平台固定于载体之上,安装于其内的驱动机构与定平台支承板相连,因此驱动机构的具体结构对系统动态特性影响很小。在进行有限元分析时可运用等效原则,将驱动电机与传动机构作为整体,等效处理为质点单元[5],对定平台仅保留支承板,其他具体结构可不予考虑。
利用有限元软件ANSYS对稳定平台的整体结构进行网格划分,系统结构的材料均为45钢,材料密度为7800kg/m3,弹性模量为206GPa,泊松比为0.3。根据稳定平台实际装配情况添加约束,接触面选用绑定和无分离两种面约束定义,对定平台外沿施加全约束。如图2所示,稳定平台仿真模型网格采用十节点正四面体二阶单元,部分区域采用二十节点六面体三阶单元,节点总数为136262,单元总数为82785。

图2 稳定平台有限元模型
2 模态分析
2.1 基本理论
模态分析是动力学分析的基础,作为一种确定系统自然频率、振型、模态参与系数等结构振动特性的技术,模态分析被广泛应用于工程振动领域。
对于一个多自由度线性振动系统,其微分方程的一般表达式为[6]:
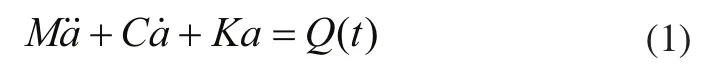
式中,M、C和K分别为n×n阶的质量、阻尼和刚度矩阵;和Q分别为广义加速度、广义速度、广义坐标和广义力的n维向量。
对无阻尼的自由振动,令外力和阻尼均为0,则方程(1)可表示为:

利用振型叠加法,可将其解假设为:

式中,φ是n阶向量,ω是振动频率,t是时间变量,t0是由初始条件确定的时间常数。
将式(3)代入式(2),即可得到如下的齐次线性方程组:

由于系统自由振动的振幅φ≠0,则有:


特征向量φ1,φ2…,φn代表系统的n个固有振型。因此,通过求解矩阵的特征值ω和特征向量φ,即可得到系统自由振动特性。
2.2 分析求解
根据稳定平台的有限元模型,对定平台支承板边缘施加位移约束,得到稳定平台的模态分析模型。运用ANSYS软件采用Block Lanczos法提取了稳定平台整机的前六阶模态,如表1所示。
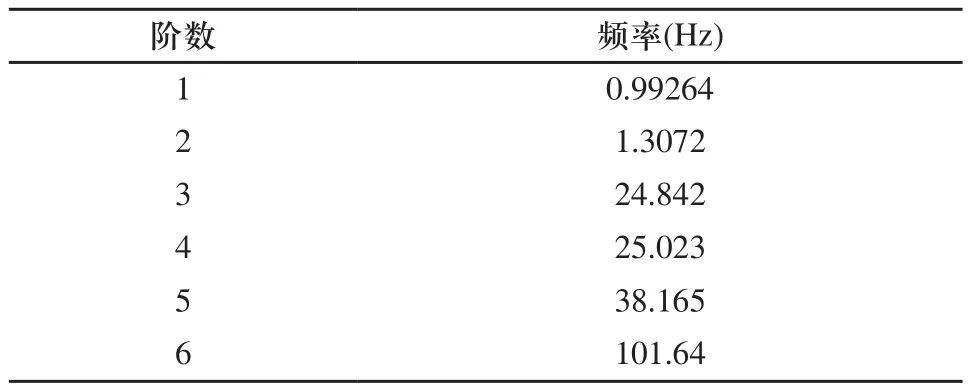
表1 稳定平台前六阶固有频率
由模态分析基本理论可知,低阶的模态对应较低的固有频率,由于该装置工作于低频率的振动环境中,因此低阶模态对该装置动态特性起决定作用。
前六阶振型图如图3所示,(a)~(f)分别为稳定平台第一阶至第六阶模态对应的振型图。

图3 稳定平台前六阶振型
通过对稳定平台各阶振型的分析可以得知:
第一阶振型频率为0.99264Hz。推杆中上部弯曲变形,定平台支承板中心垂向变形,动平台绕Y轴摆动。
第二阶振型频率为1.3072Hz。推杆中上部弯曲变形,动平台弯曲变形并绕X轴摆动。
第三阶振型频率为24.842Hz。定平台支承板中部绕X轴扭转变形极大,变形最大处位于定平台支承板电缆孔与推杆孔之间,动平台沿X轴平动。
第四阶振型频率为25.023Hz。定平台支承板中部绕Y轴扭转变形极大,变形最大处分别位于定平台支承板两电缆孔之间与两推杆孔之间,动平台沿X轴平动。
第五阶振型频率为38.165Hz。推杆中部弯曲变形极大,定平台支承板中心垂向变形明显,动平台沿Z轴运动。
第六阶振型频率为101.64Hz。虎克铰底座扭转变形,动平台绕Z轴转动。
在稳定平台整机的前六阶模态中,第一、二阶振型较为类似,仅动平台摆动轴互相垂直。第三、四阶振型较为类似,仅定平台支承板扭转轴互相垂直。平台结构变形部位集中在推杆中部、定平台支承板开孔之间、动平台边缘和虎克铰底座。
2.3 结果分析
1)根据设计指标并参考苏联涌浪等级[7]可知:该平台在低于四级海况的波浪中的摇摆频率范围为0.16Hz~2Hz。
通过模态分析提取到的稳定平台第一阶与第二阶固有频率分别为0.99264Hz和1.3072Hz,可以看出系统的固有频率处于波浪的激励频率范围之内,而推杆的脉动频率与该平台在波浪中的摇摆频率一致,故极易发生共振。虽然涌浪频率低,不会对整体结构造成伤害,但其携带的能量极大,可造成负载设备的摆幅过大导致平台倾覆。
2)根据项目前期的控制系统参数设计可知:该平台在低于四级海况工作环境下对应的的电机转速范围为1060rpm~1600rpm。
电机不同转速下的激振频率可由下式求得[8]:

式中,f为电机工作转速对应的激振频率,u为激振阶次,n为电机工作转速。求得电机对定平台的一谐次激振频率范围为:17.67Hz~26.67Hz,二谐次激励频率范围为:35.33Hz~53.33Hz。
通过模态分析提取到的稳定平台第三阶和第四阶固有频率分别为24.842Hz和25.023Hz,可以看出系统的固有频率处于电机的一谐次激振频率范围之内;第五阶固有频率为38.165Hz,处于电机的二谐次激振频率范围之内,容易发生共振。第三、四、五阶频率范围内的共振可影响陀螺仪采样精度,制约控制系统的控制性能;易使平台部分结构反复大幅变形,导致疲劳断裂;同时对其上的负载设备也有不同程度的干扰。
综上所述,该稳定平台结构设计有不合理之处,极易引发共振,必须通过结构优化来改善其动态特性,避免发生共振。
3 优化方案
为避免稳定平台可能发生的共振问题,考虑到该装置的结构及实际工作环境,最有效的方法是提高结构的固有频率,使其避开外界激励的振动频率,从而避免共振现象的发生。
固有频率与结构的刚度和质量具有如下关系[2]:

理论上刚度比质量对固有频率贡献要大,所以要提高固有频率,就可以通过提高结构的刚度,并辅以增加关键部位的质量来实现。
根据本文的仿真结果及试验情况进行分析,对稳定平台提出以下优化措施:
1)推杆刚度不足极易发生弯曲变形,需对推杆加厚加宽处理,并添加加强筋;
2)定平台支承板开孔之间及上平台外沿结构刚度不足,应设计加强筋,并适当加厚,提高刚度,防止扭转变形。
优化前后的关键部位对比如图4、图5所示。
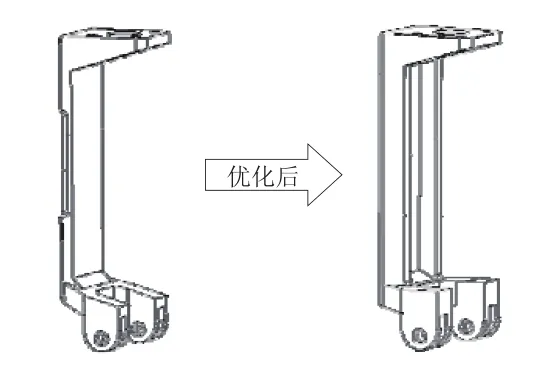
图4 推杆优化前后对比

图5 定平台支承板优化前后对比
经过对模型进行修正,并再次进行模态分析,各阶固有频率有所提高,对比结果如表2所示。

表2 优化前后稳定平台六阶固有频率对比
可以看到第一、二阶固有频率明显提高,分别达到10.924Hz和14.206Hz,避开了外界激励;第三、四阶固有频率远高于电机的工作转速对应的激振频率(一谐次激振频率范围为:17.67Hz~26.67Hz,二谐次激励频率范围为:35.33Hz~53.33Hz),故结构不会再发生共振现象。
4 结论
通过对水面浮式稳定平台进行三维建模,并对其进行模态分析,计算得到了其固有频率及各阶振型。并通过与实验数据的对比分析,找到了结构设计上的不足,并提出了结构优化方案。
通过对稳定平台结构刚度的优化,提高了整机的固有频率,有效地避免了工作过程中的共振。仿真结果证明了该方案的可行性和有效性,设备的动态特性得到改善,达到了设计指标所做出的要求。其结果为做进一步的动态特性分析和评价其动态特性提供了重要依据,并为控制系统的进一步优化提供了数据支持。
[1]张健,李军,莫宗来.基于DSP的实时自动调平控制系统设计[J].电子设计工程,2014,22(04):67-70.
[2]邓方艺,王乐勇,王晓强,等.振动条件下陀螺稳定平台漂移大的分析研究[J].装备制造技术,2007(01):34-36.
[3]莫宗来.机电式双轴实时稳定平台伺服控制技术研究[D].南京:南京理工大学,2013.
[4]姜振廷,郑忠才,董旭.基于ANSYS WORKBENCH的六自由度机械臂有限元分析及结构优化[J].制造业自动化,2014,36(01):109-110.
[5]田东升,胡明,邹平,等.基于ANSYS的六自由度工业机器人模态分析[J].机械与电子,2009(2):59-62.
[6]王勖成.有限单元法[M].北京:清华大学出版社,2003.
[7]丛滨,崔宏林,刘振.海浪模型的建立与仿真[J].西安工业大学学报,2009,29(5):475-482.
[8]杨勇,王时龙,田志峰,等.大型数控滚齿机立柱动力学仿真分析[J].中国机械工程,2013,24(11):1473-1479.

