八面体变几何桁架机器人的运动学分析及仿真研究
姜柏森,杨永胜,胡士强
(上海交通大学,上海 200240)
0 引言
变几何桁架机器人是超冗余度机器人的一种,相比于同样体积和重量的传统机器人而言,变几何桁架机器人的具有良好的优点:灵活性、模块化、刚度大和柔性。因为这些优点,变几何桁架机器人在宇宙空间,工业自动化和开发新的机器人机构方面具有广阔的应用前景。
最近,有很多文章都对变几何桁架机器人做出了深入的研究,例如有多篇文章介绍了基于神经网络方法的八面体变几何桁架机器人的运动学研究[1~3]。也有一些文章基于粒子群算法对八面体变几何桁架机器人的运动学进行了研究[4]。但是这些方法都有一些共同的缺点,就是无法用代数方法对其精确的求解,这导致了这些方法会出现计算速度慢,计算得不到最优解等特点。本文基于以上方法的缺点,结合变几何桁架机器人自身的特点提出了一种变几何桁架机器人结构,该结构不仅能够解决以上文章中出现的无法求得代数解的问题,同时使机器人运动学的运算具有很高的精度。
1 运动学模型的描述
为了解释运动学问题,首先,我们需要介绍一下单模块变几何桁架机器人的结构。
正如图1所示,一个单模块变几何桁架机器人是由两个对称的八面体桁架结构组合而成,其中两个八面体桁架有一个共同的平面M。这个联接平面同样被叫做执行平面,因为单模块变几何桁架机器人的三个可改变长度的控制器是这个平面的三条边。两个八面体桁架是关于链接平面M对称的,而其中每个八面体中与平面M相对的平面我们分别定义为底面B与顶面P。为了方便下面的计算,我们用符号表达这三个控制器的长度。在实际情况下,由于考虑到机械的实际操作上的困难,执行器平面实际上是有一定厚度的,这个厚度我们用符号来表示。这样,其执行器平面就分为上中下三个平面,三个可改变长度的控制器位于中间平面,其中我们用符号来表达低执行器平面的三个节点。对于桁架结构的其他杆,我们设计时均使其为固定长度,对于桁架模型底面与顶面的杆,其长度我们用表示,而其余侧平面的杆的长度,我们用来表示。
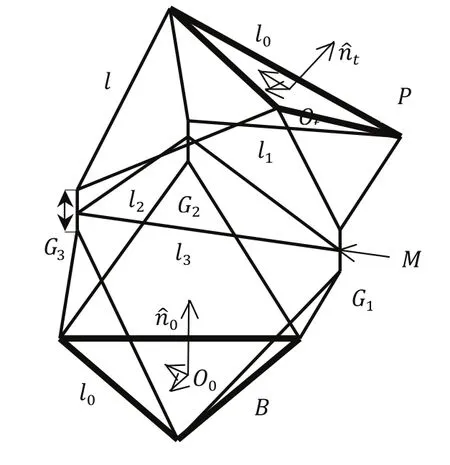
图1 单模块变几何桁架机器人的物理结构
同样的为了更为清楚的说明运动学问题,我们需要引入其他的符号。如图2所示,我们用和来表示底面中心点坐标与顶面中心点坐标。而与则被用来表示底面与顶面的法向量。用来表示从底面中心点到顶面中心点的单位向量,同时,考虑模型的对称性,它也是执行平面的法向量。最后我们用r来表示从沿着向量到达中心执行平面的长度。
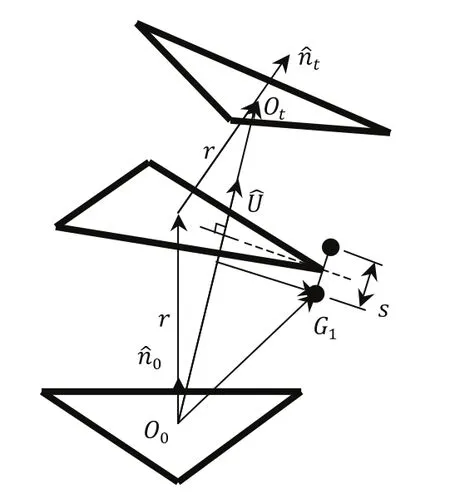
图2 运动学模型所需参数
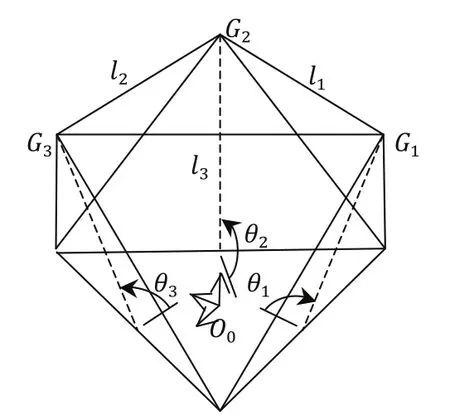
图3 中间参数
所以,通过上面所提到的符号和单模块运动学机器人模型的对称性,我们将会在接下来介绍双八面体变几何桁架机器人运动学问题。
2 单模块变几何桁架机器人运动学
单模块变几何桁架机器人运动学问题包括正向运动学问题和逆向运动学问题。下面我们将一一介绍。
2.1 单模块变几何桁架机器人的正向运动学问题
对于单模块变几何桁架机器人的正向运动学问题,我们需要通过三个控制器的长度 来计算出末端平面中心点的坐标点位置,所以正向运动学的输入变量即为而输出变量即为首先,我们应明确坐标系的定义,其坐标系定义如图4所示。
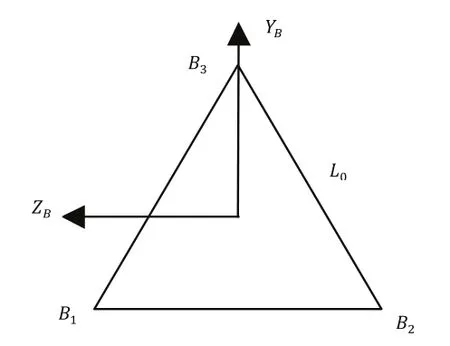
图4 机器人坐标系示意图
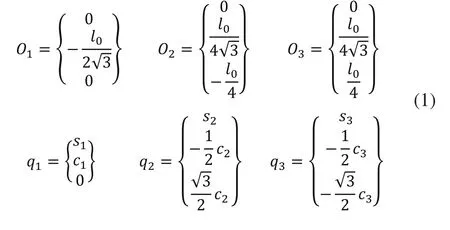
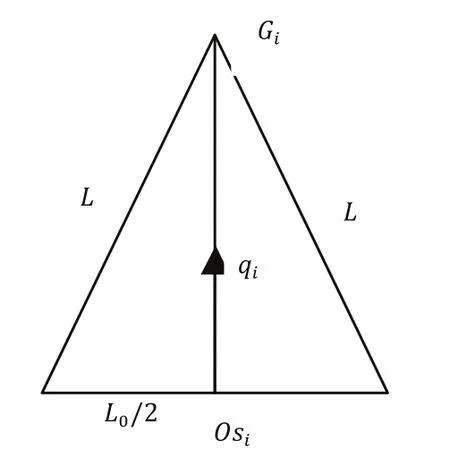
图5 侧平面三角形几何关系图
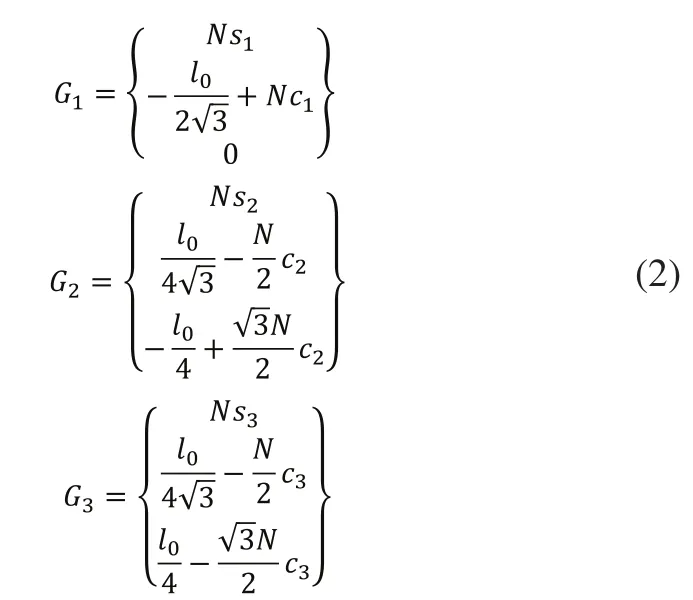
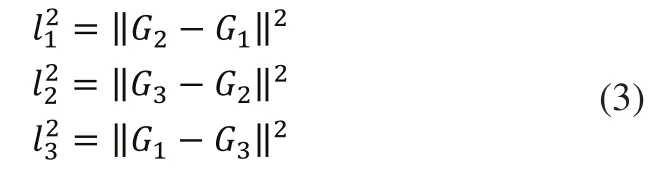
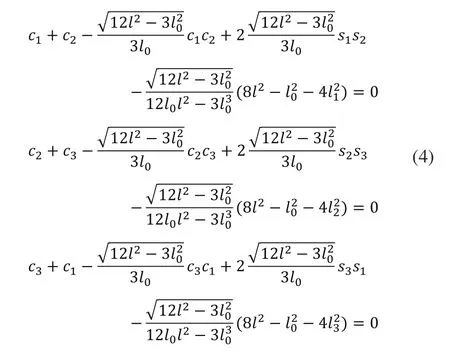
对于方程(4)来说,实际上可以求得多组不同的解,但是在实际情况下,我们可以通过不同的环境与限制条件选择一组合理的解作为最终的由于我们求得则由式(4)我们可以求得进而我们可以求得如下:
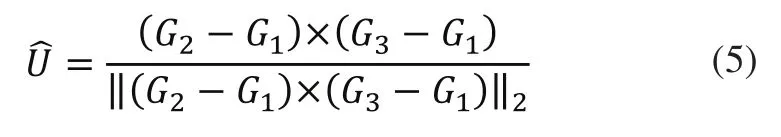
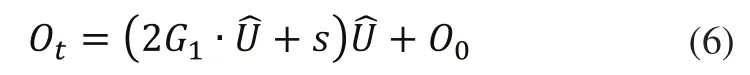
则正向运动学问题即可通过方程式(1)~式(6)最终求得。
2.2 单模块变几何桁架机器人的逆向运动学
对于单模块变几何桁架机器人的正向运动学,我们需要通过末端平面中心点的坐标点位置来计算出三个可控制器长度所以正向运动学的输入变量即为而输出变量即为同样,作为中间变量二面角是必不可少的。考虑图2所示的几何关系,我们可以得到和r如下所示。
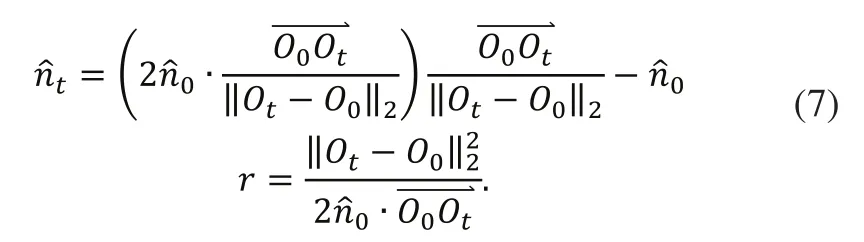
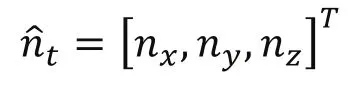
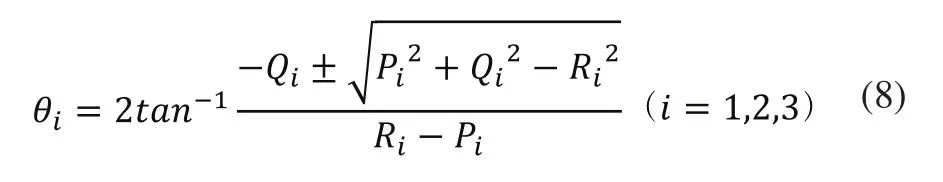
其中:
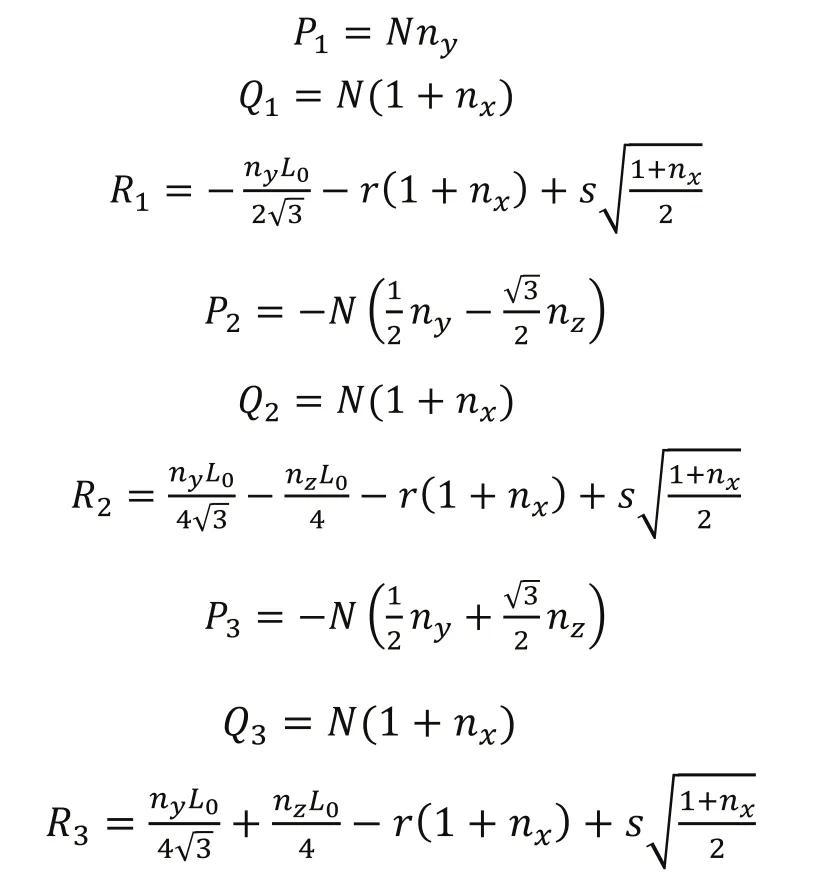
式(8)同样存在多组解,同正向运动学一样,在实际情况下,我们可以通过不同的环境与限制条件选择一组合理的解作为最终的求得后,通过式(2),我们便可以求得最终即可由式(3)求得,单模块变几何桁架机器人的逆向运动学也随之求解。
3 运动学仿真
为了进行机器人运动学计算,首先我们需要给定机器人固定参数,我们假则我们给定5组控制杆长度可以得到目标点位置如表1所示。
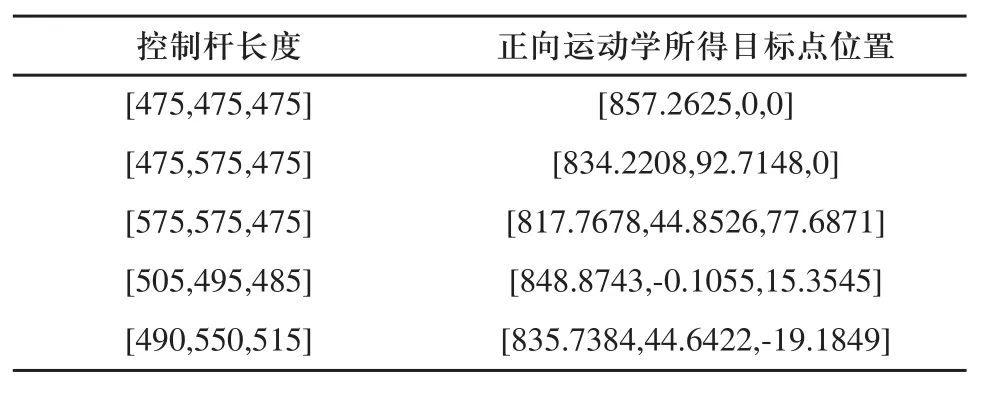
表1 正向运动学示例
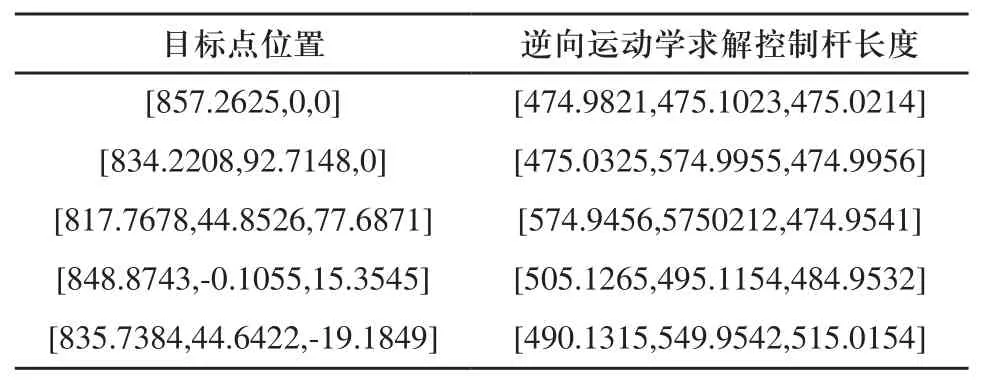
表2 逆向运动学示例
由表1与表2可知,该方法精确的解决了八面体变几何桁架机器人的运动学问题,并且其正逆向运动学能得到良好的匹配结果。
4 结论
本文在变几何桁架概念的基础上设计了一种对称双八面体变几何桁架机器人,并利用该机器人机构解决了其他八面体变几何桁架机器人无法使用代数运算求解运动学精确解的问题。并且,只要给出合理的初始参数,该方法基本可以消除正逆向运动学运算所带来的误差,使得该方法具有很好的准确性。
[1]罗佑新.八面体变几何桁架机构综合的神经网络超混沌牛顿迭代法研究[J].机械设计,2008,25(11).
[2]雷勇,徐礼钜,吴江.基于模糊神经网络的冗余度变几何桁架机器人位置控制[J].电工技术学报,2002,17(4):40-44.
[3]吴江,徐礼钜,雷勇.基于神经网络的冗余度二重八面体变几何桁架机器人运动学求解[J].四川大学学报(工程科学版),2000,32(2):90-94.
[4]易建,车林仙,陈长忆.基于粒子群算法的八面体变几何桁架机器人位置正解[J].机械工程师,2006,(7):34-36.

