浅析九年级数学中考第一轮复习

秦燕

【摘要】 很多老师在数学中考复习时将大量的时间放在难度系数较大的综合题上，而忽视对中考第一轮的复习，因而在综合运用时对基础知识、基本技能、基本方法不能熟练运用，从而影响综合题的发挥.

【关键词】 数学；中考；第一轮复习；基础；数学思想方法

众所周知，近年来中考数学的新颖性、灵活性越来越强，对学生的要求也越来越高，所以不少的师生在中考复习阶段中把主要的精力都放在了难度系数较大的综合题上，所以在中考总复习时，忽视或者看轻了对数学的第一轮复习，对一些基础知识一带而过，而将大量的时间放在第二轮尤其是第三轮的复习上，结果在综合运用时对基础知识 、基本技能、基本方法不能熟练运用，从而对综合题的感悟也觉得比较吃力. 因此，对于中考数学复习来说，第一轮复习尤为重要.

一、 紧扣《大纲》， 系统复习

在第一轮复习中，我们应该紧紧抓住教学大纲，联系新课程标准、《考试指南》和课本，将整个三年的零碎的数学知識重新整合，进行系统复习. 教研室下发的《中考总复习》中就已经把所有的知识分成七个单元：① 数与式；② 方程与不等式；③ 函数及其图像；④ 图形的认识；⑤ 图形与变换；⑥ 概率；⑦ 统计. 我们在讲每一个单元时，一般性是先讲概念，同时揭示概念、定理之间的关系. 但是不同类型的单元所采用的方法还是不一样的.

二、抓好例题、习题以及变式的教学

第一轮复习时，所采用的例题习题千万不能随意，尤其不能搞“题海战术”. 选的例题最好能选择一些覆盖知识点广的例题，尽可能使每道例题包含若干个知识点，而不仅仅局限于某一知识点. 如在复习“函数及图像”时，可以选择这样的例题：

例：已知函数y = （m + 1）x2 + 3x - m（2x + 1） + 7，求

（1）当m取何值时，对应的函数图像与x轴有两个交点；

（2）当m取何值时，方程（m + 1）x2 + 3x - m（2x - 1） - 7 = 0没有实数根

（3）当m取何值时，此函数图像一定在x轴下方.

通过这一个例题，我们就把函数知识和方程、不等式之间的知识点综合联系了. 当然，对例题和习题还可以引申扩充，挖掘出问题的内涵和外延，以提高学生分析问题和解决问题的能力. 复习时我们可以从以下几方面入手加以挖掘和深化：

① 寻找其他不同的方法；

② 改变题目形式（如可以把填空题改为选择题或者解答题）；

③ 改变题目的条件或结论，将题目进行变式练习；

④ 对结论进行进一步引申；

⑤ 可以增减条件从而探索结论；

三、注重数学方法与数学思想的训练

数学思想方法主要有整体思想，转化思想，方程思想，函数思想，数形结合思想，归纳思想，分类讨论思想，类比思想，等等. 要对数学思想有目的，有计划地渗透，不可能全部到第二轮复习中才讲.

如告诉了自变量与因变量，要求写出函数解析式，或者用函数解析式去求交点等问题，都需用到函数的思想，教师要让学生加深对这一思想的理解，多做一些相关内容的题目；方程思想，它是利用已知量与未知量之间的关系，通过建立方程把未知量转化为已知量；分类讨论思想，它是中考的热点和难点；数形结合的思想，它是沟通代数与几何的桥梁.

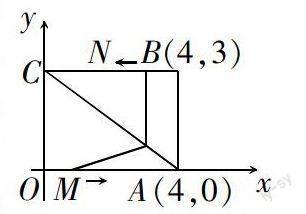
例：如图，在平面直角坐标系中，四边形OABC为矩形，点A、B的坐标为A（4，0）、B（4，3）动点M、N分别从点O、B同时出发，以每小时1个单位的速度运动，其中点M沿OA向终点A运动，点N沿BC向终点C运动，过点N作NP⊥BC交AC于点P，连接MP.已知动点运动了x秒.

（1）p点坐标为（，）（用含t的代数式表示）

（2）记△NPA的面积为s，求s与t的函数关系. （0 < t < 4）

（3）当t为何值时，s有最大值，最大值是多少？

（4）点Q在y轴上，当s为最大值且△QAN为等腰三角形时，求直线AQ的解析式.

发现其中涉及了以下一些思想：

1. 函数思想：s与t的函数关系式

2. 方程思想：将点P的横坐标代入AC直线的函数关系式中解得P得纵坐标；

3. 转化思想：将点的坐标与线段的距离的转化

4. 数形结合思想：具体的图形用代数方法求出Q点的坐标，几何问题转化成代数问题.

四、注重查缺补漏，及时总结

学生在经历了复习测试后，会有许多错题产生. 此时引导学生自己整理、归纳、订正错题就必不可少. 可以建议学生使用错题本. 要求学生不仅要写出错解的过程和订正后的正确过程，更要注明错误的原因，以免今后再犯此类错误. 当然如果题目较长，可以将题目进行剪拼，以免浪费太多时间在抄题上.

总而言之，九年级数学第一轮复习必须本着对学生、对社会、对自己负责的态度，从学生实际出发，注重对基础知识的复习，紧扣教材；注重审题能力的训练和阅读理解能力的培养；注重数学思想方法的渗透，提高学生的数学素养，一步一个脚印，相信一定能取得较好的效果.